Внешний угол треугольника
- Сумма внешних углов
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
∠1 + ∠4 = 180°.
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
∠2 + ∠3 + ∠4 = 180°.
Из этого следует, что
∠1 + ∠4 = ∠2 + ∠3 + ∠4.
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
∠1 = ∠2 + ∠3.
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.
Смежные углы в геометрии
15 июня 2022
Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.
В этом уроке:
- Что такое смежные углы
- Основное свойство смежных углов
- Биссектрисы смежных углов
- Тренировочные задачи
Это довольно простая, но очень важная тема.
1. Что такое смежные углы
Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$
Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.
Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.
Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).
Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:
А вот дальше — смежные, хотя и расположены немного непривычно:
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых
образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.
2. Основное свойство внешних углов
У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.
Теорема. Сумма смежных углов равна 180°.
Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:
Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов
[angle AMB=angle AMN+angle BMN]
Но угол $AMB$ — развёрнутый, поэтому
[angle AMN+angle BMN={180}^circ ]
Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.
Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.
Задача 1. Найдите угол, смежный с углом $ABC$, если:
- $angle ABC={36}^circ $.
- $angle ABC={121}^circ $.
Решение
1) Обозначим смежный угол $DBC=x$. Он будет тупым:
Тогда $x=180-36=144$.
2) Обозначим смежный угол $DBC=x$. Он будет острым:
Тогда $x=180-121=59$.
Немного усложним задачу.
Задача 2. Найдите смежные углы, если:
- один из них на 68° больше другого.
- один из них в 5 раз больше другого.
- их градусные меры относятся как 5 : 4.
Решение.
1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.
Поскольку углы смежные, их сумма равна 180 градусов:
[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]
Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.
2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.
Сумма смежных углов равна 180 градусов, поэтому
[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]
Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.
3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.
Сумма смежных углов вновь равна 180 градусов:
[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]
Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.
3. Биссектрисы смежных углов
Вновь рассмотрим смежные углы $AMN$ и $BMN$:
Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:
Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому
[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]
Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.
Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.
Решение. Изобразим все углы на рисунке:
Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно
[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]
Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому
[begin{align}2x+2y&=140 \ x+y&=70 end{align}]
Это и есть искомый угол между биссектрисами. Он равен 70 градусов.
Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.
Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.
С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.
Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы
- Перпендикулярные прямые — определение и свойства
- Правила комбинаторики в задаче B6
- Метод координат в пространстве
- Четырехугольная пирамида: как найти координаты вершин
- Задача B4 про три дороги — стандартная задача на движение
В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.
Определение внешнего угла
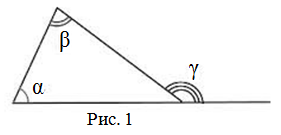
Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:
Смежный с внутренним углом (λ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ.
При этом:
- сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
- 0 и 0.
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
γ = α + β
Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Примеры задач
Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.
Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.
Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.
Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α.
Исходя из теоремы: β = γ – α = 115° – 28° = 87°.
Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65°.
Внешний угол треугольника
Определение. Внешним углом треугольника называется угол, смежный к любому углу этого треугольника.
На Рис.1 угол 4 внешний так как углы 2 и 4 смежные.
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Доказательство. Докажем, что ( small angle 4=angle 1+ angle 3. ) Поскольку сумма углов треугольника равна 180°, то имеем:
 . . |
(1) |
Так как углы 2 и 4 смежные, то:
 . . |
(2) |
Вычитая (1) из (2) получим:
 , , |
 , , |
 . . |
- Главная
- Справочник
- Теорема о внешнем угле треугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Теорема о внешнем угле треугольника
Содержание:
- Формулировка теоремы о внешнем угле треугольника
- Примеры решения задач
Формулировка теоремы о внешнем угле треугольника
Теорема
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним:
$$angle gamma=angle alpha+angle beta$$
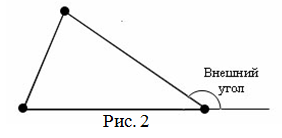
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине
(внутренним углом) (рис. 2).
Следствие
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Примеры решения задач
Пример
Задание. В треугольнике
$ABC$ угол
$A$ равен
$30^{circ}$, угол
$B — 80^{circ}$. Найти
градусную меру угла, смежного с
третьим углом треугольника.
Решение. Согласно теореме о внешнем угле треугольника, искомый угол равен сумме углов не смежных с ним, то есть:
$$alpha=30^{circ}+80^{circ}=110^{circ}$$
Ответ. $alpha=110^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В треугольнике $ABC$ угол
$A$ равен
$30^{circ}$, а внешний угол при вершине
$C$ равен
$45^{circ}$. Найти остальные углы треугольника
$ABC$ .
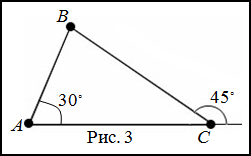
Решение. Сделаем чертеж к задаче (рис. 3).
Согласно теореме о внешнем угле треугольника, получаем равенство для нахождения градусной меры угла
$B$:
$$45^{circ}=30^{circ}+angle B Rightarrow angle B=15^{circ}$$
Угол $C$, как смежный угол, равен
$$angle C=180^{circ}-45^{circ}=135^{circ}$$
Ответ. $angle B=15^{circ}, angle C=135^{circ}$
Статьи по теме
- Теоремы по математике и геометрии
- Теорема Пифагора
- Теорема о среднем
- Теорема о сумме углов треугольника
- Теорема о трех перпендикулярах
- Все темы раздела «Теоремы по математике и геометрии»

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные