Как найти угол снаружи треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?

Определение.

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.

Как построить внешний угол треугольника? Нужно продлить сторону треугольника.

На рисунке:

∠3 — внешний угол при вершине А,

∠2 — внешний угол при вершине С,

∠1 — внешний угол при вершине В.

Сколько внешних углов у треугольника?

При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.

Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):

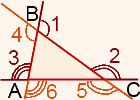
∠1=∠4, ∠2=∠5, ∠3=∠6.

Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.

Чему равен внешний угол?

Теорема (о внешнем угле треугольника)

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Дано: ∆АВС, ∠1 — внешний угол при вершине С.

Доказать: ∠1=∠А+∠В.

Доказательство:

Так как сумма углов треугольника равна 180º, ∠А+∠В+∠С=180º.

Следовательно, ∠С=180º-(∠А+∠В).

∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.

Что и требовалось доказать.

Источник

Внешний угол треугольника

Сумма внешних углов

Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:

∠1 + ∠4 = 180°.

Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:

∠2 + ∠3 + ∠4 = 180°.

Из этого следует, что

∠1 + ∠4 = ∠2 + ∠3 + ∠4.

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

∠1 = ∠2 + ∠3.

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°

Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.

Источник

Мы привыкли рассматривать треугольники, в особенности их углы, только «изнутри». Однако, знаете ли, «снаружи» треугольника тоже кипит жизнь. В этом уроке предлагаем узнать, что в геометрии треугольников имеется также внешний угол. А что же такое внешний угол? Какие свойства внешнего угла треугольника существуют? Может, есть какая-нибудь теорема о внешнем угле треугольника? Вот, сейчас будем все выяснять.

Что такое внешний угол?

Начертим треугольник $bigtriangleup{ABC}$ и построим при вершине $B$ угол, смежный с $angle{B}$. Теперь в $bigtriangleup{ABC}$ при вершине $B$ появилось два угла — один «внутри», другой «снаружи». Угол «снаружи» называется внешним углом при вершине $B$. Дадим ему определение.

Внешний угол при данной вершине — угол, смежный с углом треугольника при этой вершине.

Как обозначается внешний угол?

Углы в треугольнике обозначаются согласно вершинам, где они располагаются, либо по трем точкам.

Например, в треугольнике $bigtriangleup{ABC}$ угол при вершине $B$ обозначается как $angle{B}$, либо как $angle{ABC}$. А если при вершине $B$ в том числе имеется внешний угол? Его тоже обозначать как $angle{B}$?

Или лучше указать дополнительную точку на продолжении стороны? Вопрос отличный. Для того, чтобы подобной путаницы не возникало, в геометрии принят термин «внутренний угол».

К примеру, в ходе задачи или доказательства вы пользуетесь внешним углом при некоторой вершине. Скажем, вновь при вершине $B$ в треугольнике $bigtriangleup{ABC}$. Когда вы ссылаетесь к углу треугольника внутри, можно уточнить: «Внутренний угол $angle{B}$».

Когда ссылаетесь к углу снаружи, уточняйте: «Внешний угол $angle{B}$».

Способ с уточнениями «внутренний угол», «внешний угол» проще и не требует дополнительных точек. К тому же, такое обозначение облегчает понимание, где в треугольнике располагается угол. Ведь вы акцентируете внимание только на вершине.

Такое особенно полезно, когда решения или чертежи к задачам громоздкие. Бывает, что при одной вершине нужно рассматривать два внешних угла. Они все равно равны как вертикальные, но все же… Мало ли. Тут удобнее дать углам обозначение в стиле «$angle{1}$» или, например, «$angle{x}$».

Теорема о внешнем угле треугольника

Применим наши знания теоремы о сумме углов треугольника к внешним углам. Рассмотрим внешний угол $angle{B}$ в треугольнике $bigtriangleup{ABC}$. Сумма $angle{B}$ внешнего и $angle{B}$ внутреннего равняется $180^circ$, как смежных.

По теореме о сумме углов треугольника: $$angle{A}+angle{B}+angle{C}=180^circ$$

Если:

внутр. $angle{B}+$ внеш. $angle{B}=180^circ$
$angle{A}+$ внутр. $angle{B}+angle{C}=180^circ$

То:

внеш. $angle{B}=180^circ-$ внутр. $angle{B}$
внутр. $angle{B}=180^circ-angle{A}-angle{C}$
внеш. $angle{B}=180^circ-180^circ+angle{A}+angle{C}$

Методом подстановки переменных из одного уравнения в другое мы обнаружили, что внешний угол равняется сумме двух других углов, с ним не смежных. Так, величина внешнего $angle{B}$ равна сумме $angle{A}+angle{C}$ внутренних.

Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.

Обратим ваше внимание вот еще на что.

Раз внешний угол по величине — это сумма двух внутренних углов, внешний угол всегда будет по величине больше любого внутреннего угла, не смежного с ним. Полезное следствие, особенно если вдруг придется, скажем, доказывать возможность или невозможность существования некоторого треугольника. Или еще для чего-нибудь.

Теорема о внешнем угле треугольника: доказательство Евклида

Официально теорему о внешнем угле треугольника впервые доказал Евклид — древнегреческий математик, считающийся «отцом геометрии». Примечательно, что его доказательство не имеет ничего общего с теоремой о сумме углов треугольника — математик воспользовался свойствами углов при параллельных и секущей. Оно в принципе и понятно: Евклид огромное количество времени посвятил изучению параллельных прямых.

В качестве практики и повторения материала по параллельным прямым и секущим мы приводим евклидовое доказательство. Оно очень даже достойно внимания. Итак, посмотрим, как внешний угол треугольника «общается» с параллельными прямыми.

Доказательство

Рассмотрим $bigtriangleup{ABC}$ с внешним углом при вершине $B$. Проведем через эту вершину луч, параллельный стороне $AC$. Отметим на полученном луче точку $B_1$. На продолжении стороны $AB$ отметим точку $B_2$.

Теперь рассмотрим параллельные отрезки $BB_1$ и $AC$ при секущей $AB$. Внутренний угол $angle{A}$ и угол $angle{B_{1}BB_2}$ равны как соответственные. Далее рассмотрим отрезки $BB_1$ и $AC$ при секущей $CB$. Углы $angle{B_{1}BC}$ и $angle{ACB}$ равны как накрест лежащие.

Видим, что внешний $angle{B}$ состоит из суммы внутренних углов $angle{A}$ и $angle{C}$. Что и требовалось доказать.

Свойства внешнего угла

Не сказать, что свойства внешнего угла многочисленные. В основном, когда затрагивается внешний угол, для решения задач или доказательства чего-либо хватает теоремы о внешнем угле треугольника. Ну, и смежности внутреннего и внешнего углов.

То есть базового определения.

Правда если к делу подключается биссектриса, свойства внешнего угла, помимо «классических», таки обнаруживаются. Разберем одно наиболее полезное.

Свойство биссектрис внешнего и внутреннего углов треугольника. Биссектрисы внутреннего и внешнего углов являются перпендикулярными друг к другу.

Доказательство

Проведем в треугольнике $bigtriangleup{ABC}$ биссектрисы при внешнем $angle{B}$ и при внутреннем $angle{B}$. Для удобства разметим все полученные углы следующим образом: $x$ и $y$ — значения внутренних углов при вершинах $A$ и $C$ соответственно; $z$ — половина внутреннего $angle{B}$; $f$ — половина внешнего $angle{B}$.

Нам требуется установить, чему равняется $z+f$. Если сумма будет равна $90^circ$ — свойство доказано. Воспользуемся теоремой о внешнем угле и теоремой о сумме углов треугольника.

$$2f=x+y\2z+x+y=180^circ$$

Так как нам нужно найти сумму $z+f$, сложим уравнения выше:

$$2f+2z+x+y=x+y+180^circ$$

Видим, что после сокращения $2(f+z)=180^circ$.

Следовательно сумма $f$ и $z$ равняется $90^circ$. Биссектрисы перпендикулярны друг к другу. Свойство доказано.

Задача для самостоятельного решения

Свойства внешнего угла треугольника — нет. Теорема о внешнем угле треугольника — однозначное да. Решите данную задачу, не используя свойство смежности внешнего и внутреннего углов.

Условие. В треугольнике $bigtriangleup{ABH}$ величина внешних углов $angle{1}$ и $angle{2}$ равняется $97^circ$ и $125^circ$ соответственно. Найдите, чему равняется внутренний $angle{A}$.

Показать решение

Спрятать решение

Дано:

$bigtriangleup{ABH}$
$angle{1}=97^circ$
$angle{2}=125^circ$

Найти:

внутр. $angle{A}$ — ?

Решение. Воспользуемся теоремой о внешнем угле треугольника. Так как рассматривать мы будем только два внешних угла — $angle{1}$ и $angle{2}$, договоримся, что $angle{A}$, $angle{B}$ и $angle{H}$ далее в решении относятся к обозначению только внутренних углов треугольника $bigtriangleup{ABH}$.

Имеем следующие равенства:

$$angle{1}=angle{A}+angle{B}\angle{2}=angle{A}+angle{H}$$

Сложим между собой данные равенства и подставим имеющиеся по условию значения внешних углов $angle{1}$ и $angle{2}$:

$$2angle{A}+angle{B}+angle{H}=angle{1}+angle{2}=222^circ$$

Сумма углов $angle{A}$, $angle{B}$ и $angle{H}$ составляет $180^circ$. Вычтем из полученного выше равенства равенство $angle{A}+angle{B}+angle{H}=180^circ$.

Получаем следующее:

$$2angle{A}+angle{B}+angle{H}=222^circ\angle{A}+angle{B}+angle{H}=180^circ\angle{A}=222^circ-180^circ$$

Откуда получаем, что значение внутреннего угла $angle{A}$ равняется $42^circ$.

Ответ: $42^circ$.

Источник

Как найти внешний угол треугольника

Внешний угол треугольника является смежным внутреннему углу фигуры. В сумме эти углы при каждой из вершин треугольника составляют 180° и представляют развернутый угол.

Инструкция

Из названия очевидно, что внешний угол лежит за пределами треугольника. Чтобы представить себе внешний угол, продлите сторону фигуры за вершину. Угол между продолжением стороны и второй стороной треугольника, выходящей из этой вершины, и будет внешним для угла треугольника при данной вершине.

Очевидно, что острому углу треугольника соответствует тупой внешний угол. Для тупого угла внешний угол — острый, а внешний угол прямого угла — прямой. Два угла с общей стороной и сторонами, принадлежащими одной прямой, являются смежными и в сумме составляют 180°. Если угол треугольника α известен по условию, то смежный с ним внешний угол β определяется так:
β=180°-α.

Если угол α не задан, но известны другие два угла треугольника, то их сумма равна величине угла, внешнего по отношению к углу α. Это утверждение следует из того, что сумма всех углов треугольника равна 180°. В треугольнике внешний угол больше внутреннего угла, не смежного с ним.

Если градусная мера угла треугольника не задана, но из соотношения сторон известны тригонометрические зависимости, то по этим данным также можно найти внешний угол:
Sinα = Sin (180°-α)
Cosα = -Cos (180°-α)
tgα =- tg (180°-α).

Внешний угол треугольника можно определить, если не задан ни один внутренний угол, а известны только стороны фигуры. Из связей между элементами треугольника определите одну из тригонометрических функций внутреннего угла. Вычислите соответствующую функцию искомого внешнего угла и по тригонометрическим таблицам Брадиса найдите его величину в градусах.

Например, из формулы площади S=(b*c*Sinα)/2 определите Sinα, а затем внутренний и внешний угол в градусной мере. Или определите Cosα из теоремы косинусов a²=b²+c²-2bc*Cosα.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна $180^{circ}$ .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом alpha . Если угол alpha острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

$sin left( 180^{circ} - alpha right) = sin alpha;$
$cos left( 180^{circ} - alpha right) = - cos alpha;$
$tg , left( 180^{circ} - alpha right) = - , tg , alpha.$

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

1. В треугольнике ABC угол равен $90^{circ}$ , $cos A = genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}$ . Найдите тангенс внешнего угла при вершине .

Пусть varphi — внешний угол при вершине .

$cos varphi = - cos A = - genfrac{}{}{}{0}{displaystyle 4}{displaystyle sqrt{17}}.$

Зная , найдем по формуле:

$genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos^2 varphi}= 1 + tg^2 , varphi.$

Получим: $tg , varphi= - genfrac{}{}{}{0}{displaystyle 1}{displaystyle 4} = - 0,25.$

2. В треугольнике ABC угол равен $90^{circ}$ , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов и равна $90^{circ}$ , . Тогда и синус внешнего угла при вершине также равен 0,1 .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Внешний угол треугольника. Синус и косинус внешнего угла» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник