Как найти угол треугольника 7 класс атанасян

Геометрия

7 класс

Урок №23

Сумма углов треугольника

Перечень рассматриваемых вопросов:

• Формулирование и доказательство теоремы о сумме углов треугольника.
• Следствия теоремы о сумме углов треугольника.
• Классификация треугольников по видам углов.
• Формулирование и доказательство теоремы о свойствах прямоугольного треугольника.
• Решение задач с применением пройденного материала;
• Угловой отражатель.

Тезаурус:

Внешний угол треугольника– это угол, смежный с каким-либо углом этого треугольника.

Основная литература:

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее, на уроках математики, вы познакомились с различными геометрическими фигурами, в том числе и с треугольниками. При изучении геометрии, вы узнали признаки равенства треугольников, выяснили, что такое медиана, биссектриса и высота треугольника.

Сегодня мы продолжим изучать треугольники и рассмотрим одну из важнейших теорем геометрии– теорему о сумме углов треугольника.

Сформулируем эту теорему.

Сумма углов треугольника равна 180°.

Дано: ∆АВС.

Доказать:

∠А+∠В +∠С = 180º

Доказательство:

Проведем через вершину В прямую а ║АС.

∠1 = ∠4 (по свойству параллельных прямых, т. к. это накрест лежащие углы при пересечении прямых а и АС и секущей АВ), ∠3 = ∠5 (по свойству параллельных прямых, т. к. это – накрест лежащие углы при пересечении прямых а и АС и секущей ВС)→ ∠4 + ∠2 + ∠5 = 180° (по свойству развёрнутого угла) → ∠1 + ∠2 + ∠3 = 180° → ∠А + ∠В + ∠С = 180°.

Что и требовалось доказать.

Теперь введём ещё одно понятие, связанное с треугольниками –внешний угол треугольника. Это угол, смежный с каким-либо углом этого треугольника.

Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Дано: ∆АВС.

Доказать:

∠4 = ∠1 + ∠2.

∠3 + ∠4 = 180° (по свойству развёрнутого угла).

∠3 + (∠2 + ∠1) = 180° (по теореме о сумме углов треугольника) → ∠4 = ∠2 + ∠1.

Что и требовалось доказать.

Из теоремы о сумме углов треугольника следует, что если один из углов треугольника равен 90 градусам или больше 90 градусов, то остальные два угла будут острые, т.к. их сумма не должна превышать 90 градусов. Поэтому, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

Исходя из этого, можно классифицировать треугольники по углам.

По углам треугольник может быть:

‑ остроугольным, если все его углы являются острыми (т.е. меньше 90°);

‑ тупоугольным, если один из его углов тупой (т.е. больше 90°);

‑ прямоугольным, если один угол 90° (т.е. прямой).

В прямоугольном треугольнике стороны имеют свои названия.

Сторона треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие – катетами.

∆АВС– прямоугольный.

∠В = 90°.

АС – гипотенуза.

АВ,ВС – катеты.

Докажем свойство прямоугольного треугольника, которое устанавливается с помощью теоремы о сумме углов треугольника.

Сумма двух острых углов прямоугольного треугольника равна 90º.

Дано:

∆АВС – прямоугольный.

∠В = 90°.

Доказать: ∠А +∠С = 90°.

Доказательство:

∠А +∠С + ∠В = 180° (по теореме о сумме углов треугольника).

∠В = 90° (по определению прямоугольного треугольника) →∠А + ∠С + 90° = 180°

∠А + ∠С = 180 – 90° = 90°

Что и требовалось доказать.

Решим задачу.

Докажем, что в равностороннем треугольнике каждый угол равен 60 °.

Дано:

∆АВС – равносторонний

Доказать: ∠А =∠С = ∠В = 60°.

Доказательство:

Так как треугольник АВС равносторонний →АС = АВ = ВС (по определению равностороннего треугольника) → если АС = АВ → ∠С = ∠В (по свойству равнобедренного треугольника). Аналогично, если АС = СВ → ∠А = ∠В (по свойству равнобедренного треугольника) → ∠А = ∠С = ∠В.

∠А + ∠С + ∠В = 180° (по теореме о сумме углов треугольника).

∠А = ∠С = ∠В = 180° : 3 = 60°.

Что и требовалось доказать.

Материал для углублённого изучения темы.

Угловой отражатель.

Одно из свойств прямоугольного треугольника ‑сумма двух его острых углов равна 90°‑используется в технике, например, в угловом отражателе. Это устройство, которое отражает падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей.

Отражатель, например, устанавливается на заднем крыле велосипеда, для того, чтобы «возвращать назад» свет автомобильных фар, чтобы водитель машины видел велосипедиста ночью.

Ещё угловой отражаетель был установлен на автоматической космической станции, запущенной на Луну( выделен на рисунке кружочком), с целью определения точного расстояния от Земли до Луны.

Разбор заданий тренировочного модуля

1. Чему равна градусная мера углаА, если треугольник АВС прямоугольный?

Решение:

По условию, ∆АВС – прямоугольный → сумма его острых углов равна 90°.

∠А+∠В=90°

∠В = 45° (по рисунку) →∠А + 45° = 90°.

∠А=90° – 45° = 45°.

Ответ: ∠А = 45°.

2. По рисунку найдите угол N треугольника FNA.

Решение:

По рисунку ∠NAP= 140°, этот угол внешний к углу А треугольника FNA→

∠NAP = ∠N +∠F= 140° (т.к. внешний угол треугольника равен сумме двух углов треугольника не смежных с ним).

∠F = 60° (по рисунку).

∠N + 60° = 140°.

∠N = 140° – 60° = 80°.

Ответ:∠N = 80°.

План урока:

Сумма углов треугольника

Внешние углы треугольника

Сравнение сторон и углов треугольника

Неравенство треугольника

Сумма углов треугольника

Рассмотрим произвольный треугольник АВС. Точки А, В и С не лежат на одной прямой, а потому через В можно провести прямую a, параллельную АС. При этом прямые СВ и АВ окажутся секущими для двух параллельных прямых:

Известно, что секущие образуют пары накрест лежащие углы, причем они равны. Отметим на рисунке эти пары и обозначим их как ∠1, ∠2, ∠3 и ∠ 4.

Равные углы (∠1 = ∠2, ∠3 = ∠4) отметим одним цветом. Также обозначим ∠АВС как ∠5:

С одной стороны, углы 2, 4 и 5 вместе образуют развернутый угол, то есть их сумма равна 180°:

В результате мы получили, что сумма углов треугольника АВС в точности равна 180°! В итоге мы можем сформулировать следующую теорему:

Задание. В треуг-ке один угол равен 50°, а второй – 60°. Чему равен третий угол этого треуг-ка?

Решение. Обозначим углы треугольника как ∠1, ∠2 и ∠3.

Получили обыкновенное уравнение с одной переменной. Для его решения просто перенесем слагаемые 50° и 60° из левой части в правую:

Задание. Докажите, что у любого треуг-ка есть хотя бы один угол, который не превосходит 60°.

Решение. Докажем это утверждение методом «от противного». Пусть существует такой треуг-к, у которого каждый из углов больше 60°. Это можно записать в виде трех неравенств:

В итоге имеем, что в сумме эти углы больше 180°, а это невозможно. Это противоречие, следовательно, треуг-к с тремя углами, каждый из которых больше 60°, не существует.

Задание. Основанием рав-бедр. ∆АВС является сторона АС. Известно, что ∠В = 40°. Чему равны ∠А и ∠С этого треуг-ка?

Решение. Сначала необходимо вспомнить важное свойство – углы равнобедренного треугольника при его основании равны друг другу. В нашем случае это значит, что ∠А = ∠С:

Задание. Один из углов при основании рав-бедр. треуг-ка равен 50°. Найдите два других угла.

Решение. Построим рисунок по условию задачи:

Отдельного внимания заслуживает равносторонний треуг-к. Напомним, что у него равны все три стороны. Построим его:

Теперь подумаем о том, чему равны его углы. С одной стороны, мы можем рассматривать ∆АВС как рав-бедр. с основанием АС, ведь AB = BC. Тогда∠А = ∠С. Но с другой стороны, всё тот же ∆АВС мы можем одновременно считать и рав-бедр. с основанием АВ, ведь АС = ВС. Из этого следует, что ∠А = ∠С. В итоге получаем, что все три угла ∆АВС равны:

Итак, получили удивительный факт – в равностороннем треуг-ке все углы равны 60°!

Рассмотрим чуть более сложную задачу, где неизвестен ни один из углов треуг-ка, однако известны некоторые соотношения между ними.

Задание. Первый угол треуг-ка больше второго в 2 раза, а третий равен сумме первых двух углов. Чему равны углы треуг-ка?

Решение. Для большей наглядности примем первый угол треуг-ка за неизвестную величину, то есть за х. Тогда второй угол будет равен 2х, а третий окажется равным их сумме:

Внешние углы треугольника

Построим некоторый треуг-к, а потом продлим одну из его сторон. На рисунке мы продлили сторону АС. В результате образуется угол, который называют внешним углом треугольника:

На рисунке видно, что ∠ВСD является внешним. Но одновременно можно утверждать и ещё один факт – углы ∠АСВ и ∠ВСD являются смежными. Это позволяет нам дать следующее определение:

В итоге мы доказали, что внешний угол треугольника равен сумме двух углов треуг-ка, которые с ним не смежны.

Задание. У ∆АВС ∠А = 50°, ∠В = 75°. Найдите величину внешнего угла, смежного с ∠С.

Решение. В данном случае, согласно доказанному нами правилу, достаточно просто сложить ∠А и ∠B:

Рассмотрим ещё несколько более тяжелых задач.

Задание. В ∆АВС проведены биссектрисы угловА и B. Они пересекаются в точке М. Известно, что ∠А = 58°, ∠B = 96°. Найдите ∠АМB.

Решение. Устно такую задачу не решить, поэтому построим рисунок:

АМ – это биссектриса, а она разбивает∠ВАС на два равных угла. Поэтому мы можем вычислить ∠ВАМ:

Отметим найденные углы на рисунке:

Обратите внимание на ∆АВМ, который выделен красным цветом. Теперь мы знаем два угла в нем. Значит, можно найти и третий! Запишем для ∆АВМ сумму его углов:

Задание. Построен внешний угол равнобедренного треугольника, который смежен с вершиной, лежащей против основания. Далее построили биссектрису этого внешнего угла. Докажите, что эта биссектриса будет параллельна основанию.

Решение. Выполним построение:

Пусть АС – это основание рав-бедр. ∆АВС. Тогда внешний угол должен быть проведен к вершине В, ведь именно она лежит против основания. Обозначим внешний угол как ∠СВD (для этого мы просто добавили точку Dна продолжение отрезка АВ). Далее проводим биссектрису ВК. Нам требуется доказать, что ВК||АС.

Поступим очень просто – обозначим неизвестную нам величину угла при основании как х. То есть

В результате мы получили, что и ∠С, и ∠CBK равны х, то есть они равны и друг другу. Однако эти углы являются накрест лежащими для прямых АС и ВК и секущей ВС. Из равенства накрест лежащих углов следует, что АС||ВК.

Задание. В ∆АВС проведена медиана АМ, причем ее длина равна ВМ. Найдите ∠А.

Решение. Напомним, что медиана – это прямая, разбивающая сторону на два равных отрезка. То есть ВМ = МС. По условию АМ = ВМ, значит, имеет место двойное равенство:

Посмотрите на рисунок – здесь есть сразу два рав-бедр. треуг-ка! Это ∆АВМ (с основанием АВ) и ∆АМС (с основанием АМС). Обозначим∠В как х, а ∠С – как у. Углы при основании рав-бедр. треуг-ков одинаковы, а потому

Сравнение сторон и углов треугольника

Докажем следующую теорему:

Построим ∆АВС, в котором сторона АВ будет длиннее, чем АС. Нам надо доказать, что ∠С >∠B:

Выполним дополнительное построение – отметим на прямой АВ такую точку D, что AD = АС. Точка D будет располагаться на отрезке АВ, ведь АВ больше АС, а, значит, и больше АD. Также соединим C и D отрезком:

Теперь рассмотрим ∆ADC. Он является рав-бедр., ведь AD = AC. Из этого следует, что ∠ADC = ∠ACD.

Можно заметить, что ∠АDС является внешним углом для ∆BDC. Это значит, что

Мы доказали только первую часть теоремы. Теперь надо доказать обратное утверждение – против большего угла находится большая сторона треугольника. Предположим обратное, что существует ∆АВС, в котором ∠С>∠B, но не выполняется условие АВ >AC. Тогда либо АВ = ВС, либо АВ <ВС. Первый вариант означает, что ∆АВС – рав-бедр., но тогда ∠С =∠B, что противоречит условию. Если же АВ <ВС, то по только что доказанному утверждению ∠С<∠B, что также противоречит исходному условию. Поэтому АВ >AC.

Задание. В ∆АВС известны углы:

Запишите стороны этого треуг-ка в порядке возрастания.

Решение. Всё очень просто – чем больше сторона, тем против большего угла она лежит. Поэтому самая большая сторона – это АВ, вторая по длине – АС, а наименьшая сторона – ВС. То есть BС<AС<AВ:

Доказанная теорема помогает сформулировать важный признак рав-бедр. треуг-ка:

Действительно, против равных углов должны лежать равные стороны, в противном случае сложится ситуация, когда в треуг-ке против сторон разной длины будут лежать равные углы, что невозможно.

Задание. В рав-бедр. ∆АВС основанием является АС. Из точек А и С проведены биссектрисы, которые пересеклись в точке О. Докажите, что ∆АОС также является рав-бедр.

Решение.

Ясно, что ∠ВАС = ∠ВСА, так как это углы при основании рав-бедр. ∆АВС. С другой стороны, ∠ОАС равен половине ∠ВАС, ведь АО – биссектриса:

В итоге имеем, что ∠ОАС и ∠АСО равны. Но тогда в ∆АОС есть два одинаковых угла, а потому он является рав-бедр. (АО = ОС).

Неравенство треугольника

Следующая важная теорема называется неравенством треугольника:

Попробуем доказать неравенство треугольника. Возьмем произвольный ∆АВС и покажем, что сторона АВ меньше, чем величина ВС + АС. Для этого «дорисуем» к отрезку АС ещё один отрезок СD, равный BC, при этом АС и СD должны лежать на одной прямой:

Так как AD = АС + СD, то нам достаточно показать, что АВ <AD. Ясно, что ∆ВСD является рав-бедр., ведь ВС = СD. Это значит, что

Получается, что в ∆АВD сторона АВ лежит против меньшего угла по сравнению со стороной АD. Значит, эта сторона должна быть меньше АD, что мы и пытаемся доказать.

Доказанная теорема означает, что не всякий треуг-к можно построить по его сторонам. Так, у нас никогда не получится построить треуг-к, у которого стороны равны 2, 3 и 7 см, так как одна из этих длин больше, чем сумма двух других:

7 > 2 + 3

Верно обратное утверждение – если все заданные длины удовлетворяют неравенству, то треуг-к построить можно.

Задание. Известны две стороны равнобедренного треугольника, они равны 25 и 10 см. Какая из них является основанием?

Решение. Рассмотрим сперва случай, когда основание равно 25 см. Тогда две другие стороны имеют длину 10 см. Их сумма (10 см + 10 см = 20 см) меньше основания. Такая ситуация невозможно из-за неравенства треуг-ка.

Ситуация же, при которой основание имеет длину 10 см, вполне допустима. Тогда две другие стороны равны 25 см, и для каждой стороны неравенство треуг-ка выполняется:

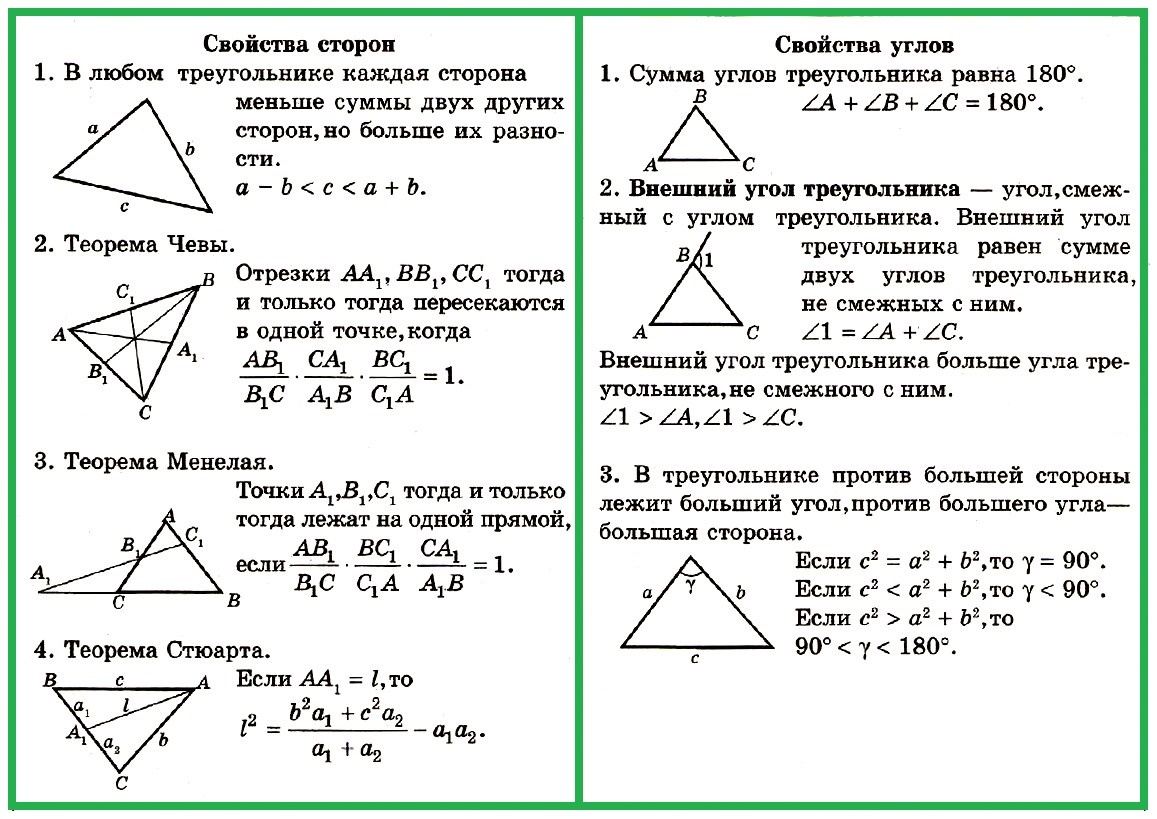
«Свойства сторон и углов треугольника
+ ЗАДАЧИ по теме»

---

---

Свойства углов
1. Сумма углов треугольника равна 180°.
2. Внешний угол треугольника — угол, смежный с углом треугольника.
3. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
4. Внешний угол треугольника больше угла треугольника, не смежного с ним.
5. В треугольнике против большей стороны лежит больший угол, против большего угла — большая сторона.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

Задача № 1.
Дано: AB = BC, CD AB, ∠ABC = 32. Найти: ∠ACD

Задача № 2.
Дано: ABC, AB = BC, ∠DBC — внешний угол ABC, ∠DBC = 52. Найти: ∠BAC, ∠BCA.

Задача № 3.
Дано: ABC, AB = BC, ∠C = 64, AD — биссектриса ∠A. Найти: ∠ADB.

Задача № 4.
Дано: AD = DB, BK = KC, ∠BAD = 38, ∠BCK = 26. Найти: ∠BDK, ∠BKD, ∠DBK.

---

Это конспект по теме «Свойства сторон и углов треугольника». Выберите дальнейшие действия:

• Перейти к следующему конспекту: Прямоугольный треугольник
• Вернуться к Списку конспектов по геометрии