Как найти угол треугольника по клеточкам

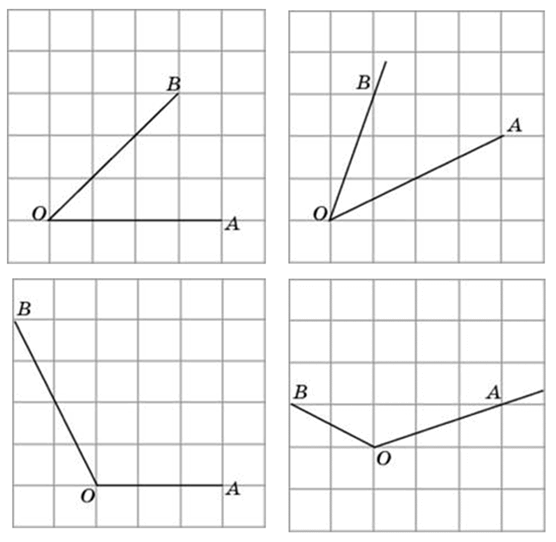
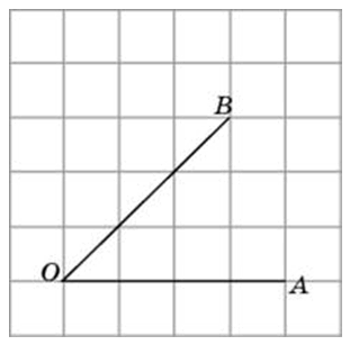
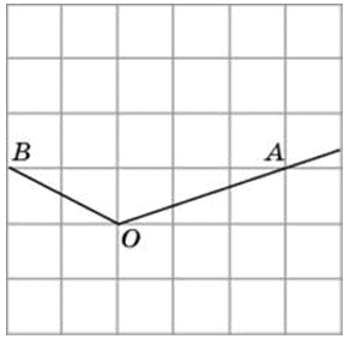
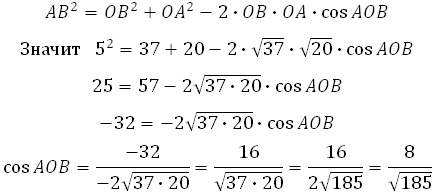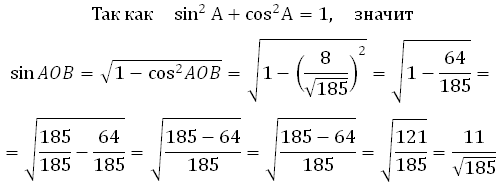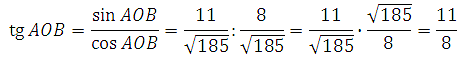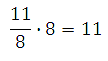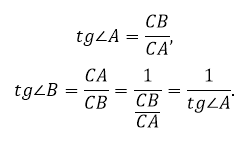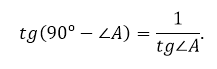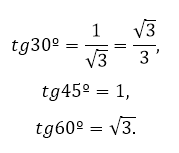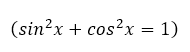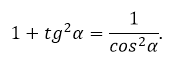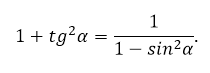Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:

Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:

Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.

То есть tg(BOA) = DB / DO.

Чтобы найти DO и DB достаточно будет посчитать количество клеточек.

DO = 2.

DB = 5.

Значит, tg(BOA) = 5 / 2 = 2,5.

Зная тангенс, мы можем легко найти и котангенс:

ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.

_

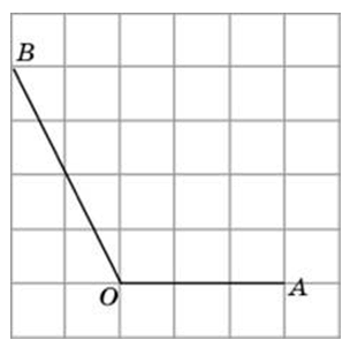
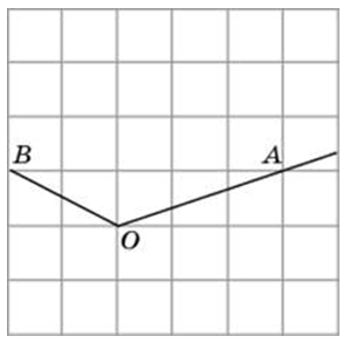
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):

Если соединить точки A и B, то угол ABO будет прямым.

И тангенс можно вычислить как отношение BA к BO.

Как же нам их найти?

И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).

Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.

Таким образом, у нас получится следующее:

tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.

И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.

Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике. 

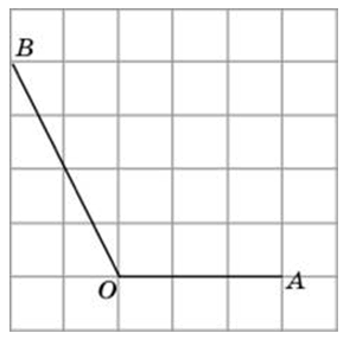
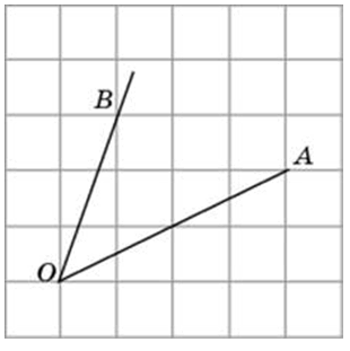
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):

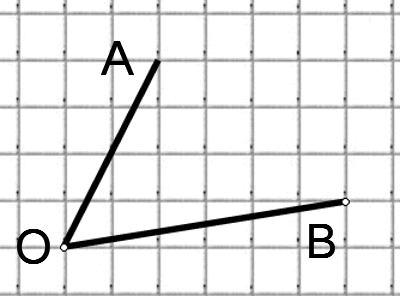
Итак, рассмотрим задание:

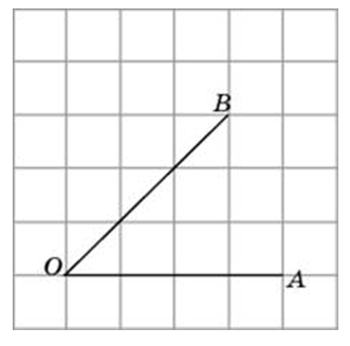
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.

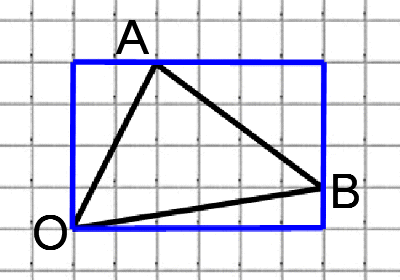
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.

Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).

АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,

ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1, 

OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,

По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус  угла между ними.

Из основного тригонометрического тождества можем найти sin AOB:

*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение. 

Теперь можем найти тангенс:

Умножим результат на 8 и запишем ответ:

Ответ: 11

Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.

Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.

Посмотреть решение

Найдите тангенс угла AOB.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.

Посмотреть решение

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на  два корня из двух.

Посмотреть решение

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.

Посмотреть решение

Найдите тангенс угла AOB.

Посмотреть решение

В данной рубрике продолжим рассматривать задачи, не пропустите!

С уважением, Александр Крутицких.

*Делитесь информацией в социальных сетях )

На клетчатой бумаге изображён вписанный угол

Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.

Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?

Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?

Начнём с самого простого. Чему равен данный угол?

Конечно же, 90 градусам.

Чему равен этот угол?

Понятно, что 45 градусам.

Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).

225 градусов (180 + 45 или 360 – 135).

Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.

Ещё раз напомню основное свойство вписанного угла.

«Вписанный угол равен половине центрального,

опирающегося на ту же дугу»

27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.

Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.

Построим центральный угол соответствующий дуге ВС:

Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:

По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).

27887. Найдите величину угла ABC . Ответ дайте в градусах.

27888. Найдите величину угла ABC. Ответ дайте в градусах.

27889. Найдите величину угла ABC . Ответ дайте в градусах.

27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.

Нужно знать свойство вписанного угла (обязательно).

Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.

На этом всё. Успеха Вам!

С уважением, Александр Крутицких

Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».

Как найти угол треугольника по клеткам в окружности

На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.

Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.

На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.

Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:

Найдите угол ABC. Ответ дайте в градусах.

Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.

Как находить угол по клеткам в окружности

На клетчатой бумаге изображён вписанный угол

Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.

Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?

Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?

Начнём с самого простого. Чему равен данный угол?

Конечно же, 90 градусам.

Чему равен этот угол?

Понятно, что 45 градусам.

Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).

225 градусов (180 + 45 или 360 – 135).

Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.

Ещё раз напомню основное свойство вписанного угла.

«Вписанный угол равен половине центрального,

опирающегося на ту же дугу»

27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.

Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.

Построим центральный угол соответствующий дуге ВС:

Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:

По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).

27887. Найдите величину угла ABC . Ответ дайте в градусах.

27888. Найдите величину угла ABC. Ответ дайте в градусах.

27889. Найдите величину угла ABC . Ответ дайте в градусах.

27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.

Нужно знать свойство вписанного угла (обязательно).

Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.

На этом всё. Успеха Вам!

С уважением, Александр Крутицких

Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».

Как находить угол по клеткам в окружности

На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.

Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.

На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.

Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:

Найдите угол ABC. Ответ дайте в градусах.

Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.

Подготовка к ОГЭ. «Углы на клетках»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Углы на клетках

Как построить прямой угол по клеткам? Очень просто! – скажете вы. – Отметим точку, вершину угла, от неё чертим вправо или влево луч, затем ещё один луч вверх или вниз. Угол между горизонталью и вертикалью – прямой. А можно и по диагоналям соседних клеток.

Всё верно. А если один из лучей уже построен и он не горизонтальный, не вертикальный и не проходит по диагоналям клеток? Как начертить второй луч, чтобы угол между ними был прямым?

Найдём узел сетки, через который проходит начерченный луч. На нашем рисунке до такого узла от начала луча нужно пройти 3 клетки ВЛЕВО и 1 клетку ВНИЗ. Поэтому чтобы получился прямой угол, надо от начала луча отсчитать 1 клетку ВЛЕВО и 3 клетки ВВЕРХ. Почему? Обозначим упомянутые нами точки – А, В и О. Построим векторы ОА и ОВ. Координаты вектора ОА равны (-3; -1), вектора ОВ (-1; 3). Их скалярное произведение равно 0, поэтому они перпендикулярны.

Можно отсчитывать клетки и так: 1 клетку ВПРАВО и 3 клетки ВНИЗ. Тогда вектор ОВ имеет координаты (1; -3), при этом скалярное произведение векторов ОА и ОВ также равно 0.

Вывод. Векторы с координатами ( a ; b ) и (- b ; a ), или ( a ; b ) и ( b ; — a ), — перпендикулярны.

Рассмотрим несколько задач, связанных с умением находить прямой угол на рисунке.

№ 1 . Найти угол АВС на рисунке.

Решение. На первом рисунке угол АОС построен на диагоналях соседних клеток. На втором рисунке векторы ОА и ОС имеют координаты соответственно (3; -4) и (4; 3). Поэтому на первом и втором рисунках центральный угол АОС – прямой, а вписанный угол АВС, опирающийся на ту же дугу, равен его половине, то есть 45 ° . На третьем рисунке угол АОС – половина прямого, то есть 45 ° , а угол АВС соответственно равен 22,5 ° .

№ 2. Три квадрата расположены так, как показано на рисунке. Чему равен угол между прямыми АС и В D ?

Решение. Отрезок В D переместим параллельно вниз на одну клетку. Появляется отрезок АМ, равный В D . Угол между прямыми АС и В D равен углу между АС и АМ на втором рисунке. Соединим отрезком точки С и М. Получается, что угол АМС – прямой и АМ = МС. Треугольник АСМ прямоугольный равнобедренный, поэтому искомый угол равен 45°.

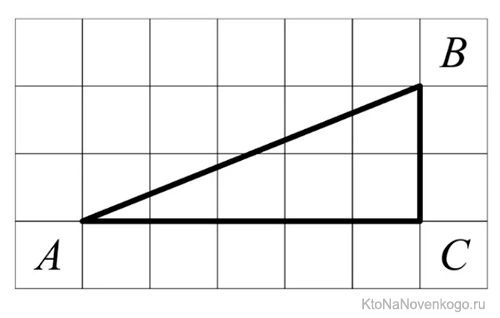
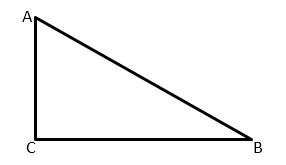
№ 3. Найти тангенс угла, изображенного на рисунке.

Решение. Выделим на этом рисунке узлы сетки – точки А и С. Рассмотрим треугольник АВС. Заметим, что он является прямоугольным, к тому же катет ВС в 2 раза больше катета АС. Отсюда следует, что тангенс угла В равен 1:2 = 0,5.

Правильный треугольник и описанная около неё окружность, построенные на клетках, несут в себе много интересных свойств. Известно, что радиус окружности, описанной около равностороннего треугольника со стороной а, равен , а радиус вписанной в него окружности — , то есть в два раза меньше. Отсюда следует, что хорда, перпендикулярная радиусу окружности и проходящая через его середину, является стороной правильного треугольника. Другими словами, острый вписанный угол, опирающийся на хорду, перпендикулярную радиусу и проходящую через его середину, равен 60 ° , а центральный угол и тупой вписанный угол, опирающиеся на эту хорду, — 120 ° .

Рассмотрим несколько примеров задач, решаемых на основе этого свойства.

Угол АВС на рисунке равен 60 ° , так как хорда АС проходит через середину радиуса и перпендикулярна ему.

Угол АВС на рисунке является половиной угла в 60 ° из предыдущей задачи и равен 30 ° .

Угол АВС на следующем рисунке равен 120 ° . При этом четырёхугольник АВСО является ромбом и его острый угол равен 60 °.

Полезным при решении задач на клетках является знание углов правильных многоугольников . Рассмотрим правильный шестиугольник и правильный восьмиугольник. Около них описаны окружности. Каждый внутренний угол правильного шестиугольника равен 120 ° , угол между диагоналями-диаметрами равен 60 ° , угол между двумя соседними диагоналями, исходящими из одной вершины, равен 30 ° , меньшая диагональ правильного шестиугольника перпендикулярна его стороне, а с другими соседними сторонами — угол 30 ° . Каждый угол правильного восьмиугольника равен 135 °, угол между соседними диагоналями-диаметрами равен 45°.

Найдите на следующих рисунках градусные меры отмеченных углов.

Углы на клетках

-1-

Как построить прямой угол по клеткам? Очень просто! – скажете вы. – Отметим точку,
вершину угла, от неё чертим вправо или влево луч, затем ещё один луч вверх или
вниз. Угол между горизонталью и вертикалью – прямой. А можно и по диагоналям
соседних клеток.

                 

Всё верно. А если один из лучей уже построен и
он не горизонтальный, не вертикальный и не проходит по диагоналям клеток?  Как
начертить второй луч, чтобы угол между ними был прямым?

                        

Найдём узел сетки, через который проходит
начерченный луч. На нашем рисунке до такого узла от начала луча нужно пройти 3
клетки ВЛЕВО и 1 клетку ВНИЗ. Поэтому чтобы получился прямой угол, надо от
начала луча отсчитать 1 клетку ВЛЕВО и 3 клетки ВВЕРХ. Почему?  Обозначим 
упомянутые нами точки – А, В и О. Построим векторы ОА и ОВ. Координаты вектора ОА
равны (-3; -1), вектора ОВ (-1; 3). Их скалярное произведение равно 0, поэтому
они перпендикулярны.

Можно отсчитывать клетки и так: 1 клетку
ВПРАВО и 3 клетки ВНИЗ. Тогда вектор ОВ имеет  координаты (1; -3), при этом
скалярное произведение векторов ОА и ОВ также равно 0.

                  

Вывод. Векторы с координатами (a; b) и (-b; a), или
(a; b) и (b; —a), — перпендикулярны.

Рассмотрим несколько задач, связанных с
умением находить прямой угол на рисунке.

№ 1. Найти угол АВС на рисунке.

          

Решение.  На первом рисунке угол АОС построен
на диагоналях соседних клеток. На втором рисунке векторы ОА и ОС имеют
координаты соответственно (3; -4) и (4; 3). Поэтому на первом и втором рисунках
центральный угол АОС – прямой, а вписанный угол АВС, опирающийся на ту же дугу,
равен его половине, то есть 45°. На третьем рисунке угол АОС – половина прямого,
то есть 45°, а угол АВС соответственно равен 22,5°.

№ 2. Три квадрата расположены так, как  показано на рисунке. Чему равен
угол между прямыми АС и ВD?

Решение. Отрезок ВD
переместим параллельно вниз на одну клетку. Появляется отрезок АМ, равный ВD. Угол
между прямыми АС и ВD равен углу между АС и АМ на втором рисунке.
Соединим отрезком точки С и М. Получается, что угол АМС – прямой и  АМ = МС. Треугольник
АСМ прямоугольный равнобедренный, поэтому искомый угол равен  45°.

№ 3. Найти тангенс угла, изображенного на рисунке.

              

Решение.  Выделим на этом рисунке узлы сетки –
точки А и С. Рассмотрим треугольник АВС. Заметим, что он является
прямоугольным, к тому же катет ВС в 2 раза больше катета АС. Отсюда следует,
что тангенс угла В равен 1:2 = 0,5.

-2-

Правильный треугольник  и описанная около неё
окружность, построенные на клетках, несут в себе много интересных свойств. Известно,
что радиус окружности, описанной около равностороннего треугольника со стороной
а, равен , а радиус вписанной в него окружности — , то есть в два раза меньше. Отсюда
следует, что хорда, перпендикулярная радиусу окружности и проходящая через его
середину, является стороной правильного треугольника. Другими словами, острый
вписанный угол, опирающийся на хорду, перпендикулярную радиусу и проходящую
через его середину, равен 60°, а центральный угол и тупой вписанный угол,
опирающиеся на эту хорду, — 120°.

Рассмотрим несколько примеров задач, решаемых
на основе этого свойства.

1)      Угол АВС на рисунке равен 60°,
так как хорда АС  проходит через середину радиуса и перпендикулярна ему.

2)      Угол АВС на рисунке является половиной угла в
60° из предыдущей задачи и равен 30°.

                          

3)      Угол АВС на следующем рисунке равен 120°.
При этом четырёхугольник АВСО является  ромбом и его острый угол равен 60°.

                             

-3-

Полезным при решении
задач на клетках является знание углов правильных многоугольников. Рассмотрим
правильный шестиугольник и правильный восьмиугольник. Около них описаны
окружности. Каждый внутренний угол правильного шестиугольника равен 120°,
угол между диагоналями-диаметрами равен 60°, угол
между двумя соседними диагоналями, исходящими из одной вершины, равен 30°,
меньшая диагональ правильного шестиугольника перпендикулярна его стороне, а с другими
соседними сторонами — угол 30°. Каждый угол правильного восьмиугольника
равен 135°, угол между соседними
диагоналями-диаметрами равен 45°.

           

Найдите на следующих
рисунках градусные меры отмеченных углов.

                         

          

             

      

Мясникова Т.Ф.

Что такое тангенс угла и как его найти

Живущим людям на Земле
всегда хотелось знать,
как путь найти в пустыне, море,
и можно к звёздам ли попасть.

Хотелось труд свой облегчить,
создать машины, чтоб летать.
И чтоб вопросы разрешить,
пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Тангенс угла

Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.

В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.

Для понимания связи между объектами рассматриваются отношения различных отрезков. Задавая связь между ними, вводят понятия синуса, косинуса (это что?), тангенса, котангенса.

Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.

Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.

Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.

Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).

Тангенс — это отношение…

Итак, есть два определения:

1. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

   Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.

2. Тангенс – это отношение синуса к косинусу.

   Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.

Приняты обозначения:

Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan⁡(α).

Как найти тангенс угла (формулы)

Первое свойство тангенса вытекает из его определения как отношения катетов.

Сумма двух непрямых углов прямоугольного треугольника равна 90º. Поэтому

Так как тангенс – это отношение катетов, то

Получается, что

Учитывая особенности некоторых треугольников (равностороннего, прямоугольного, равнобедренного), а также записанное свойство, была составлена таблица значений тангенса для углов 30º, 45º, 60º.

В частности,

Задача нахождения других углов по значению тангенса была решена с помощью составления более обширных таблиц. За счёт появления современных вычислительных средств необходимость применения табулированных значений уменьшилась.

Как найти тангенс по клеточкам

Учитывая первое определение, можно определить, как найти его по клеточкам. Рисунок дополняется перпендикулярными линиями (строится высота), затем считается количество клеточек в полученном прямоугольном треугольнике на катетах, противолежащем и прилежащем искомому углу, а затем берётся их отношение.

Благодаря второму определению, задачу, как найти тангенс угла, можно решить, минуя таблицы и построение прямоугольных треугольников. Достаточно знать синус и косинус, связанные между собой основным тригонометрическим тождеством:

Из формулы тангенсов, записывающей кратко второе определение

и основного тригонометрического тождества можно понять, как найти тангенс, зная только косинус или синус угла.

Достаточно поделить основное тригонометрическое тождество на квадрат косинуса, подставить формулу тангенса. В результате получится его зависимость от косинуса:

Если выразить в последнем случае косинус, то запишется связь между тангенсом и синусом: