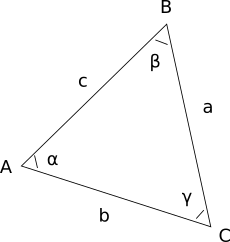
Как найти угол, если даны вершины треугольника
Треугольник — это простейший многоугольник, для нахождения величин углов которого по известным параметрам (длинам сторон, радиусам вписанных и описанных окружностей и др.) существует несколько формул. Однако часто встречаются задачи, требующие расчета углов в вершинах треугольника, который помещен в некоторую пространственную систему координат.
Инструкция
Если треугольник задан координатами всех трех своих вершин (X₁,Y₁,Z₁, X₂,Y₂,Z₂ и X₃,Y₃,Z₃), то начните с вычисления длин сторон, образующих тот угол треугольника (α), величина которого вас интересует. Если любую из них достроить до прямоугольного треугольника, в котором сторона будет гипотенузой, а ее проекции на две оси координат — катетами, то ее длину можно найти по теореме Пифагора. Длины проекций будут равны разности координат начала и конца стороны (т.е. двух вершин треугольника) по соответствующей оси, а значит, длину можно выразить как квадратный корень из суммы квадратов разностей таких координатных пар. Для трехмерного пространства соответствующие формулы двух сторон треугольника можно записать так: √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) и √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Используйте две формулы скалярного произведения векторов — в данном случае векторами с общим началом являются стороны треугольника, образующие вычисляемый угол. Одна из формул выражает скалярное произведение через их длины, полученные вами на предыдущем шаге, и косинус угла между ними: √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) * √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²) * cos(α). Другая — через сумму произведений координат по соответствующим осям: X₁*X₃ + Y₁*Y₃ + Z₁*Z₃.
Приравняйте эти две формулы и выразите из равенства косинус искомого угла: cos(α) = (X₁*X₃ + Y₁*Y₃ + Z₁*Z₃) / (√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) * √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²)). Тригонометрическая функция, определяющая величину угла в градусах по значению его косинуса, называется арккосинусом — используйте ее для записи окончательного варианта формулы нахождения угла по трехмерным координатам треугольника: α = arccos((X₁*X₃ + Y₁*Y₃ + Z₁*Z₃) / (√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) * √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²))).
Видео по теме
Источники:
- треугольник задан вершинами найти высоту
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти угол треугольника по его координатам
Если известны координаты всех трех вершин треугольника, можно найти и его углы. Координаты точки в трехмерном пространстве — x,y и z. Однако через три точки, которые являются вершинами треугольника, всегда можно провести плоскость, поэтому в этой задаче удобнее рассматривать только две координаты точек — x и y, считая координату z для всех точек одинаковой.
Пусть точка A ABC имеет координаты x1, y1, точка B этого треугольника — координаты x2, y2, а точка C — координаты x3, y3. Что представляют из себя координаты x и y вершин треугольника. В декартовой системе координат с перпендикулярными друг другу осями X и Y от начала координат можно провести радиус-векторы ко всем трем точкам. Проекции радиус-векторов на координатные оси и будут давать координаты точек.
Пусть тогда r1 — радиус вектор точки A, r2 — радиус-вектор точки B, а r3 — радиус-вектор точки C.
Очевидно, что длина стороны AB будет равна |r1-r2|, длина стороны AC = |r1-r3|, a BC = |r2-r3|.
Следовательно, AB = sqrt(((x1-x2)^2)+((y1-y2)^2)), AC = sqrt(((x1-x3)^2)+((y1-y3)^2)), BC = sqrt(((x2-x3)^2)+((y2-y3)^2)).
Углы треугольника ABC можно найти из теоремы косинусов. Теорему косинусов можно записать в следующем виде: BC^2 = (AB^2)+(AC^2) — 2AB*AC*cos(BAC). Отсюда, cos(BAC) = ((AB^2)+(AC^2)-(BC^2))/2*AB*AC. После подстановки в это выражения координаты, получится: сos(BAC) = (((x1-x2)^2)+((y1-y2)^2)+((x1-x3)^2)+((y1-y3)^2)-((x2-x3)^2)-((y2-y3)^2))/(2*sqrt(((x1-x2)^2)+((y1-y2)^2))*sqrt(((x1-x3)^2)+((y1-y3)^2)))
Найти угол треугольника зная координаты
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Стороны треугольника заданы уравнениями:
Найти координаты вершин треугольника.
Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:
Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем
Вершина A имеет координаты
Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:
получаем .
Координаты вершины C получим, решая систему из уравнений сторон BC и AC:
Вершина C имеет координаты .
http://kalk.top/sz/corners-pr-triangle
http://planshet-info.ru/kompjutery/kak-najti-ugol-treugolnika-znaja-koordinaty
| A ( ; ), B ( ; ), C ( ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Углы прямоугольного треугольникаКалькулятор расчёта углов прямоугольного треугольникаПрямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°). Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b. Формула тангенса
Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x. Углы треугольникаСумма углов треугольника всегда равна 180 градусов: Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°. Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле: Острый угол — угол, значение которого меньше 90°. У прямоугольного треугольника один угол прямой, а два других угла — острые. Как найти угол треугольника зная координаты вершинОтветПроверено экспертомДлина сторон треугольника Найдем угол между векторами AB(-3;3) и AC(1;-3) Найдем угол между векторами BA(3;-3) и BC(4;-6) Тогда третий угол, если А=153°, В=11°, С=180°-(153°+11°)=16° 1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис; 2) система линейных неравенств, определяющих треугольник; 2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам; 3) внутренние углы по теореме косинусов; 4) площадь треугольника; 5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами; 10) параметры вписанной и описанной окружностей и их уравнения. Внимание! Этот сервис не работает в браузере IE (Internet Explorer). Запишите координаты вершин треугольника и нажмите кнопку. |
A ( ; ), B ( ; ), C ( ; ) |
Даны вершины треугольника…
Расчет треугольника на плоскости
Краткая теория
Косинус угла между двумя векторами:
Угловой коэффициент прямой, перпендикулярной
данной:
Координаты середины отрезка:
Уравнение прямой, проходящей через две точки:
Уравнение прямой, проходящей через заданную точку в заданном
направлении:
Пример решения задачи
Задача
Даны
вершины
треугольника.
Найти:
1) внутренний угол
в радианах с точностью до 0,0001; 2) уравнение
высоты, проведенной через вершину
; 3) уравнение медианы проведенной через
вершину
; 4) систему линейных неравенств, определяющих
внутреннюю область треугольника
. Сделать чертеж.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1) Внутренний угол
найдем как угол между векторами
и
:
Косинус угла
:
Искомый угол:
2) Высота,
проведенная через вершину
будет перпендикулярна стороне
:
Уравнение
:
Угловой коэффициент:
Угловой коэффициент высоты:
Высота, опущенная из
вершины
:
Искомое уравнение
высоты:
3)
Медиана проходит через точку
-середину стороны
:
Уравнение
медианы
:
-уравнение медианы
4)
Найдем уравнение стороны
:
Найдем
уравнение стороны
:
Уравнения
сторон треугольника:
Система
неравенств, определяющих треугольник
:
Сделаем
чертеж:
Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:
- длину стороны a — стороны, противолежащей вершине А
- длину стороны b — стороны, противолежащей вершине B
- длину стороны c — стороны, противолежащей вершине C
- значение угла α при вершине A
- значение угла β при вершине B
- значение угла γ при вершине C
- периметр треугольника
- площадь треугольника
Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором.
Параметры треугольника по координатам вершин
Вершина А
Вершина B
Вершина C
Точность вычисления
Знаков после запятой: 2
Расчет треугольника по координатам вершин
Длины сторон находятся по формуле вычисления расстояния между точками в декартовых координатах
Углы — из формул скалярного произведения векторов при вершинах.
Периметр находится простым суммированием длин сторон.
Площадь треугольника находится через определитель