Загрузить PDF
Загрузить PDF
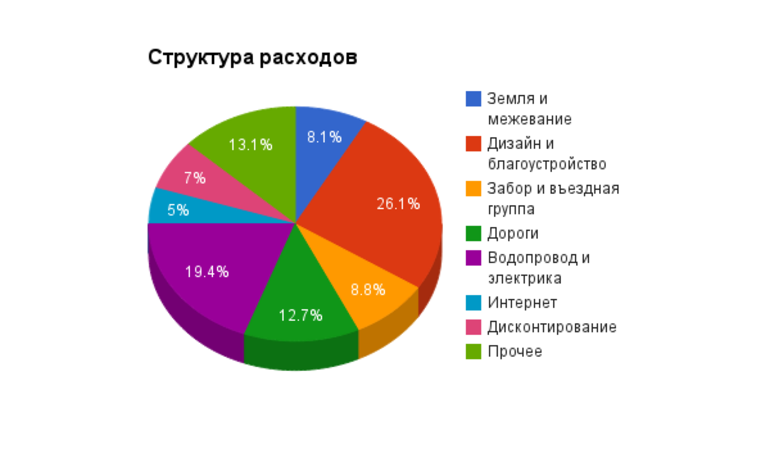
Круговые диаграммы — один из видов зонных диаграмм, которые легко понять. Они показывают части от общего количества и являются полезным инструментом при анализе опросов, статистики, сложных данных, доходов или расходов. Такие диаграммы весьма информативны — аудитория может видеть то, что происходит. Используйте круговые диаграммы для того, чтобы сделать отличную презентацию школьных и рабочих проектов.
-
1
Рассчитайте круговую диаграмму (ее пропорции).
-
2
Соберите числовые данные и запишите их в столбик в порядке убывания.
-
3
Найдите общую сумму всех значений (для этого просто сложите их).
-
4
Для каждого значения вычислите его процент от общей суммы; для этого разделите каждое значение на общую сумму.
-
5
Вычислите угол между двумя сторонами каждого сектора круговой диаграммы. Для этого умножьте каждый найденный процент (в виде десятичной дроби) на 360.
- Логика процесса в том, что в окружности 360 градусов. Если вы знаете, что число 14 400 составляет 30 % (0,3) от общей суммы, то вы вычисляете 30 % от 360: 0,3*360=108.
- Проверьте расчеты. Сложите вычисленные углы (в градусах) для каждого значения. Сумма должна равняться 360. Если это не так, то была допущена ошибка и необходимо все пересчитать.
-
6
Используйте циркуль, чтобы нарисовать круг. Чтобы нарисовать круговую диаграмму, необходимо начать с идеальной окружности. Сделать это можно с помощью циркуля (и транспортира для измерения углов). Если у вас нет циркуля, попробуйте использовать любой круглый предмет, например, крышку или CD-диск.
-
7
Проведите радиус. Начните с центра окружности (точки, в которую вы ставили иглу циркуля) и проведите прямую линию до любой точки на окружности.
- Прямая линия может быть вертикальной (соединяет 12 и 6 часов на циферблате) или горизонтальной (соединяет 9 и 3 часа на циферблате). Создавайте сегменты, двигаясь последовательно по или против часовой стрелки.
-
8
Положите транспортир на окружность. Поместите его на окружности таким образом, чтобы центр линейки транспортира совпадал с центром окружности, а отметка 0 градусов совпадала с проведенным выше радиусом.
-
9
Нарисуйте сегменты. Нарисуйте сегменты, с помощью транспортира отложив углы, вычисленные в предыдущих шагах. Каждый раз при добавлении сегмента (рисовании нового радиуса) соответственно вращайте транспортир.
- При нанесении угловых отметок убедитесь, что они хорошо видны.
-
10
Раскрасьте каждый сегмент. Вы можете использовать разные цвета, типы линий или просто слова (обозначения) в зависимости от того, что лучше отвечает вашим целям. Добавьте название и проценты для каждого сегмента.
- Раскрасьте каждый сегмент круговой диаграммы в определенный цвет для удобства просмотра результатов.
- Если вы рисуете диаграмму карандашом, перед раскрашиванием диаграммы обведите ее контуры ручкой или фломастером.
- Названия и цифры в каждом сегменте запишите по горизонтали и по центру (на одинаковом расстоянии от края для каждого сегмента). Так читать их будет удобнее.
Реклама
Советы
- Более сложные формы круговой диаграммы включают выделение сегмента через его удаление или построение разрезанной диаграммы, где каждый сегмент изображен отдельно от другого. Это можно сделать вручную или с помощью компьютерной программы.
- Если у вас не очень хороший циркуль, легче нарисовать круг, удерживая циркуль и вращая бумагу.
- Такие объекты, как монеты или флаги, можно превратить в круговые диаграммы (для визуальной привлекательности).
- Убедитесь, что суммы найденных процентов равна 100 %.
- Набравшись опыта в построении таких диаграмм, можете сместить перспективу круговой диаграммы, превратив ее в 3D или многослойную диаграмму. Это более продвинутые формы круговой диаграммы и требуют более детальной работы и знаний.
- Используйте разные цвета для выделения секторов диаграммы.
- Дважды проверьте, что все углы точны.
- Помните, что все хорошие графики имеют название и подписи.
- Тщательно проверьте расчеты — если они неверны, график будет неправильным.
Реклама
Предупреждения
- Всегда проверяйте свою работу, чтобы убедиться, что расчеты верны.
Реклама
Что вам понадобится
- Циркуль (или круглый предмет)
- Транспортир
- Карандаш и бумага
- Ластик
- Маркеры или цветные карандаши
- Калькулятор
Об этой статье
Эту страницу просматривали 190 738 раз.
Была ли эта статья полезной?
Содержание:
- § 1 Круговая диаграмма
- § 2 Решение задач с помощью круговой диаграммы
- § 3 Краткие итоги урока
§ 1 Круговая диаграмма
В этом уроке познакомимся с круговыми диаграммами и выясним, для чего они нужны.
Но сначала давайте рассмотрим чертежи. Рассмотрев представленные на чертежах углы и измерив их, мы можем сказать, что
угол АОВ =70° – центральный угол, а угол AВС = 40° – вписанный угол.
Центральный угол – это угол, вершина которого совпадает с центром окружности.
Вписанный угол – это угол, вершина которого принадлежит окружности, а стороны пересекают ее.
Обратите внимание на чертеж с центральным углом АОВ=70°.
Можем ли мы вычислить, сколько градусов содержит остальная часть круга?
Целый круг содержит 360°.
А значит, чтобы вычислить, сколько градусов содержит остальная часть круга, нужно: 360° – 70° = 290°.
Мы знаем, что сон человека составляет в сутки 8 часов, а остальное время – 16 часов – бодрствование. Рассмотрим рисунок:
Этот рисунок помогает нам наглядно увидеть распределение времени за сутки.
Такой рисунок называется круговой диаграммой.
Диаграмма – наглядный способ представления разных числовых данных.
Рассмотрим таблицу:
Обратите внимание на числовые данные таблицы, если их сравнить, то окажется, что Тихий океан – самый большой, Атлантический – почти вдвое меньше Тихого, Индийский – еще меньше, а самый маленький океан – Северный Ледовитый. Но, чтобы сделать такой вывод, нам пришлось потрудиться, сравнивая числа.
А теперь посмотрите на круговую диаграмму, демонстрирующую те же самые числовые данные.
Изображение площади океанов Земли на круговой диаграмме позволяют нам без всяких усилий и быстрее установить все перечисленные закономерности. Ведь известно, что человек лучше воспринимает и запоминает те сведения, которые представлены наглядно.
А как построить круговую диаграмму по имеющимся величинам?
Чтобы построить круговую диаграмму, надо найти центральные углы, соответствующие данным величинам.
Круг в нашей диаграмме содержит площадь всех океанов, найдем это значение:
178 млн. км² + 92 млн. км² + 75 млн. км² + 15 млн. км² = 360 млн. км²
С другой стороны полный круг содержит 360°, поэтому центральному углу в 1° соответствует площадь в 1 млн. км².
Значит, площади океанов мы можем изобразить соответственно центральными углами 178°, 92°, 75°, 15°.
Итак, чертим круг и отмечаем центр, от которого проводим луч, от построенного луча будем отмерять первый угол.
Для этого проведём второй луч под углом 178°, от следующего луча отмеряем 92°, далее – 75°, и оставшаяся часть у нас получается 15°.
Для наглядности каждую часть круга мы можем раскрасить в разные цвета и подписать названия соответствующих океанов.
Таким образом, мы построили круговую диаграмму по имеющимся величинам.
§ 2 Решение задач с помощью круговой диаграммы
Давайте решим задачу.
Вода занимает 7/10 поверхности Земли, а суша – 3/10 её поверхности.
Сколько градусов должны содержать части круга, изображающие площадь воды и суши на Земле, если считать, что полный круг изображает всю поверхность Земли?
Решение:
Так как целый круг содержит 360° и изображает всю поверхность Земли, то, чтобы найти, сколько градусов должна содержать часть круга, изображающая площадь воды на Земле, надо 360° : 10 × 7 = 252°.
Аналогично узнаем, сколько градусов должна содержать часть круга, изображающая площадь суши: 360° : 10 × 3 = 108°.
Зная теперь центральные углы, мы можем начертить круговую диаграмму, где синим цветом лучше обозначить площадь воды, а красным – площадь суши.
Решим ещё одну задачу.
Вася собирает коллекцию «Киндер-сюрпризов».
Ему попалось 15 крокодильчиков, 9 львят, 6 машинок и 6 вертолетиков.
Построить круговую диаграмму по представленным числовым данным.
Решение:
Сначала вычислим центральные углы.
Сколько всего игрушек-сюрпризов у Васи?
15 + 9 + 6 + 6 = 36 (шт.) всего игрушек-сюрпризов.
Сколько градусов содержит угол, соответствующий одной игрушке?
360° : 36 = 10° – приходится на 1 игрушку.
Сколько градусов содержат центральные углы, соответствующие каждому виду игрушек на круговой диаграмме?
10° · 15 =150° – крокодильчики;
10° · 9 = 90° – львята;
10° · 6 = 60° – машинки, столько же – вертолетики.
Строим диаграмму.
Чертим круг и отмечаем центр.
Из центра круга проводим луч, от которого будем отмерять первый угол.
Проводим из центра круга второй луч под углом 150°.
От второго луча отмеряем 90° и проводим следующий луч.
Далее отмеряем 60° и также проводим очередной луч.
Оставшаяся часть у нас получается 60°.
Раскрасим получившиеся части круга в разные цвета и укажем соответствующие названия.
§ 3 Краткие итоги урока
Подведем итоги урока:
1.Центральный угол – это угол, вершина которого совпадает с центром окружности.
2.Целый круг содержит 360°.
3.Диаграмма – наглядный способ представления разных числовых данных.
4.Чтобы построить круговую диаграмму, надо найти центральные углы, соответствующие данным величинам.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1 / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
Statistics deals with the study of collecting data, analyzing the data, interpreting, organizing, and presenting the data. In statistics to represent the information or data, we use bar graphs, piecharts, tables, graphs, picturing, and so on. The frequency in statistics tends to represent a set of data by a representative value which would define the entire collection of data.
In this article, we learn one of the data representations used in statistics that is the pie chart. Here we are learning how to construct a pie chart, pie chart definition, formula, Examples on Pie charts, advantages and disadvantages of the pie chart.
Do Read: Construction of Bar Graphs
Pie Chart – Definition
A pie chart may be a sort of pictorial representation of information or data. It represents the data in the circular graph. A pie chart requires a list of numerical variables and categorical variables. The term ‘ pie’ represents the total, and also the slices represent the parts of the total. The slice of the pie shows the relative size of the data.
A pie chart is also called a pie diagram. A pie diagram is additionally referred to as a circle chart. Pie diagrams are also replaced by some other graphs such as graphs, line graphs, histograms, line plots, and etc. The statistical data is divided into sectors or slices. Each sector represents a proportionate part of the total. In order to find the composition of something pie charts are used.
Pie Chart Formula
A pie chart is one of the important types of data representation. The pie chart total of all is equal to 360 degrees and the total value of the pie chart is always 100%. It contains different segments and sectors It contains different in which each segment and sector of a pie chart form a certain portion of the total percentage.
The following are the steps given below, we consider these steps for the pie chart formula:
- Categorize the data into meaningful data.
- Calculate the total of collected data.
- According to the heads, divide the categories
- Convert numbers into percentages
- Finally, calculate the degrees means convert percentage into degrees.
Hence the pie chart formula is, (given data / Total value of data ) x 360
How to Construct a Pie Chart?
The pie chart is extensively used because it is easy to read the data and access the data. The pie chart makes the size of the portion easy to understand. Below are the steps the data can be represented by a pie chart by using the circle graph formula.
Step 1: Initially, the data will be entered into the table.
Step 2: Next, we add the values in the table to get the total.
Step 3: We get the total, that total divides each value by the total and multiply by 100 to get a percent.
Step 4: To know how many degrees needed for each pie sector, take a full circle of 360 degrees then we follow the calculations below,
The central angle of each component = (Value of every component/ sum of values all the components) x 360°.
Step 5: By using the protractor draw the circle and measure the degree of each sector.
Advantages of Pie Chart
The pie chart will be used to represent the data and comparing the data with others is easy. The advantages of the pie chart are listed below:
- Pie charts give the audience the best visual of statistics.
- It can summarize an outsized large set of information with minimal explanation.
- You can comprehend it with little knowledge of math.
- Compared to other graphs pie chart will be easy to understand and easy to set up.
- It clearly indicates the part to the whole relationship between the values.
- We can manipulate pieces of information within the kind of sectors during a pie chart.
Disadvantages of Pie Chart
Some of the disadvantages also there for using pie charts to represent the information. The disadvantages of the pie chart are listed below,
- Angles are difficult to estimate.
- No exact numerical data.
- A pie chart can only have one set of information.
- Sometimes it is hard to tell which sections are bigger.
- You can only use it for expressing data out of an entire.
Example Problems on Pie Chart
Example 1:
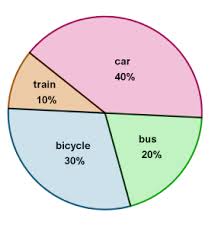
The following pie charts the data shows the percentage of types of transport, suppose of 100 people use most often
i) How many people use the car most often?
b) How many people don’t use trains most often?
c) How many people use bicycles or buses most often?
Solution:
Given the 100 people most often used transport vehicle data.
The total frequency is denoted by N. So N = 100.
(i) Given the data of 100 people’s vehicle usage
now we can find the number of people’s often car
40% of 100 people use cars most often.
So, 40%. 100 = 0.4 x 100 = 40 people.
(ii) Given the data of 100 people’s vehicle usage
Now we can find the number of people’s don’t often train
10% of 100 people use train most often.
Therefore, (100%- 10%) x 100 = 0.9 x 100= 90 people.
So, based on the result 90 people don’t use the train most often.
(iii) Given the data of 100 people’s vehicle usage
Now we can find the number of people’s often buses or bicycle
30% of 100 people use bicycles most often and 20% of them use the bus most often.
So, we get ( 30% + 20%) x 100 = 50%. 100 = 0.5 x 100 = 50
Therefore, 50 people use bicycles or buses most often.
Example 2:
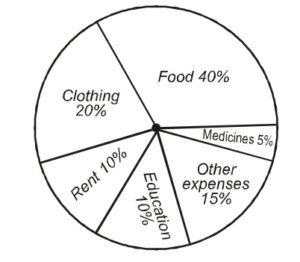
‘A ‘ lists down her monthly expenditure as follows. Based on the given data draw the Pie Chart?
| Expenditure | Amount (Percentage) |
|---|---|
| Food | 40% |
| Clothing | 20% |
| Rent | 10% |
| Education | 10% |
| Medicines | 5% |
| Other Expenses | 15% |
Solution:
Given the ‘A’ monthly expenditure in the table follow.
Now, Construct a pie chart of the given data.
Steps of construction of chart for a given data
- First, find the central angle for each component using the formula of given data.
- Draw a circle of any radius and horizontal radius.
- Starting with the horizontal radius, draw radii, making central angles likes the values of respective components.
- Repeat the method for all the components of the given data.
- These radii divide the entire circle into various sectors.
- Now, shade the sectors with different colors to denote various components. Thus we obtained the required pie chart.
Frequently Asked Questions on Pie Chart
1. List the examples of a pie chart?
Many real-time examples of a pie chart are there. Some of them are listed,
- Representation of marks obtained by students during a class.
- Representation of mobile brands in the market.
- Different brands sales comparison.
- Types of Movie comparison.
2. How do you explain Pie Chart?
A Pie Chart is a type of graph that displays data in a circular graph. The pieces of the graph are proportional to the fraction of the entire in each category. In other words, each slice of the pie is relative to the dimensions of that category within the group as an entire.
3. How to calculate the percentage of data in the pie chart?
Measure the angle of each slice of the pie chart and divide by 360 degrees. Now multiply the value by 100. The percentage of particular data will be calculated.
4. How do you find the angle for a pie chart?
To measure the angle of every segment in the pie chart. Keep the straight 0° line marked on the protractor on one among the straight sides of a segment and browse the degrees marked on the protractor on the opposite straight side of the segment. The answer is that the angle of the segment or the slice.
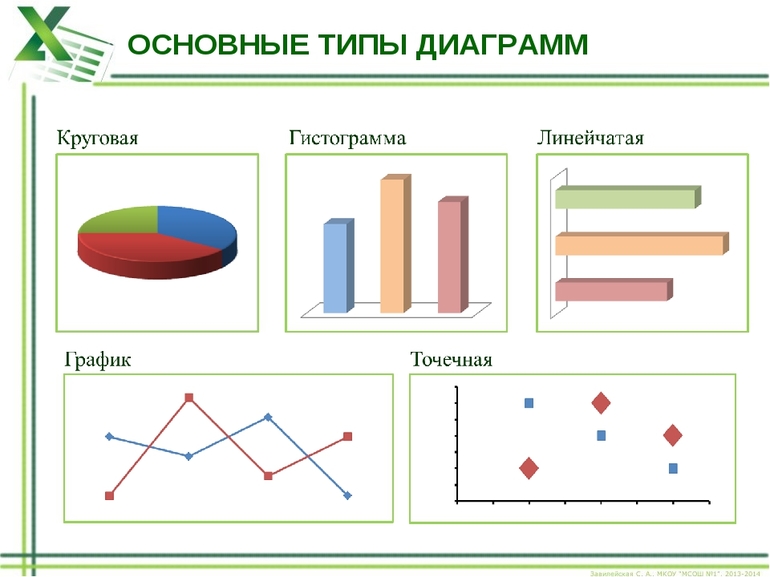
Примеры графиков
Графики бывают столбчатые, круговые, радиальные, областные биржевые, двухмерные, трехмерные и другие, которые включают в себя ещё и множество подтипов — каждый со своим определением. Продвинутые графики могут выглядеть непонятно и отпугивать молодых математиков, но их задача — графически отражать множество условий. Поэтому в школе изучение графиков начинают с 5 класса с простых фигур, задача которых — показывать простые соотношения.
Составляющие фигуры
Именно в 5 классе начинают изучение этой фигуры, поскольку она простая и наглядная. В тетрадь чертят двухмерный круг, который в дальнейшем будет вмещать в себя сектора. Сектор — это элемент фигуры, занимающий определенную ее часть, который графически отображает часть от общего. Чем меньше количество секторов в фигуре, тем более точной и она становится. Считается, что точность диаграммы падает, если она вмещает более 7 секторов. Сектора размещаются как в площади круга, так и на отдалении.
Процентные значения можно показать в секторе, если позволяет размер, если нет — значения выносят в отдельный график или столбец. Части диаграммы окрашивают в разные цвета, каждый из которых соответствует её составляющей.
Пошаговое черчение
Для того чтобы составить гистограмму, необходимо найти пропорции секторов. Первоначальные значения вносят в таблицу или столбик в порядке убывания или увеличения. Затем числа суммируют и исчисляют процентное соотношение каждого сегмента. Для этого нужно значение сектора поделить на общую сумму и умножить на 100%. Когда для каждого сектора будет получено процентное значение — начинается сложный этап работы.
Расчеты углов и значений
Нужно рассчитать угол сектора на круговой диаграмме. Для начала вспоминаем, что круг — геометрическая фигура, которая имеет аж 360 градусов. Значение сектора умножаем на 360 и делим на 100%. Результат — угол сектора. Умножить на 100%, поделить на 100%, можно ведь этого не делать? Да, можно, но тогда мы не получим численного выражения доли сектора в массиве.
Следующий этап работы — рисование круга циркулем, разметка секторов по градусам транспортиром и зарисовка полученной диаграммы цветными карандашами. Чтобы завершить выполнение — можно нарисовать цветные кружки, которые соответствуют секторам, а рядом указать их процентные значения.
Более подробная схема и примеры построения круговых, столбчатых, радиальных и других диаграмм рассмотрены в учебниках по математике за 5−6 класс, например в учебнике Н. Я. Виленкина.
Области применения
Благодаря диаграммам стало возможным визуально оценить соотношение величин и их процентную долю в массиве, а не только основываясь на сухих цифрах. Использование круговых гистограмм обрело широкую популярность благодаря своей простоте. Даже обычная семья, нарисовав в тетради, например, круглый график, можно получить графическое отображение:
- Дневной активности.
- Времени бодрствования и отдыха.
- Ежемесячных трат.
Свое применение диаграммы нашли в географии, чтобы решать многие задачи: отображение соотношения вод в мировом океане, отображения разницы содержания полезных ископаемых в разных рудах и грунтах и пр. В биологии и медицине можно использовать графики для наглядности изменения жизненных процессов на различных этапах развития человеческого организма — от рождения до старения.
Подтипы диаграмм
Стоит сказать, что эта диаграмма — основная и первичная, которую можно разделить на вторичные фигуры с вторичными сегментами, которые могут использоваться для уточнения графика. И строить их можно бесконечно. Например, первичная диаграмма — это загруженность производства на протяжении 4 сезонов — зимы, весны, лета и осени. Из этого первичного круга можно построить 4 вторичных — загруженность в каждую неделю месяца. Дальше — загруженность в отдельные дни, часы и секунды, если нужна такая точность. Использование таких графиков на компьютерах — особенно удобное, поскольку:
- Можно править в режиме реального времени.
- График трехмерный.
- Правки отображаются на графике сразу.
- Расчет градуса сектора происходит автоматически.
С круговыми диаграммами, как и с графиками в целом, стоит быть знакомым, хотя бы потому, что они часто наблюдаются в новостных сводках, статистиках и рабочих отчетах.
Главная особенность и главный минус круговой диаграммы — невозможность изображения отрицательных значений, что несколько ограничивает область её применения. Но такой вид подачи удобен и понятен для широкой аудитории, поскольку видна общая картина происходящего.
Математика
6 класс
Урок № 13
Круговые диаграммы
Перечень рассматриваемых вопросов:
- Круговые диаграммы.
- Построение круговой диаграммы.
- Решение математических задач с использованием круговых диаграмм.
Тезаурус
Одну сотую часть числа (величины) называют процентом этого числа (величины).
Диаграмма – графическое представление данных, чтобы наглядно показать соотношение целого и его частей.
Центральный угол – это угол, вершина которого совпадает с центром окружности.
Прямой угол равен 90 градусов.
Развёрнутый угол равен 180 градусов.
Острый угол больше 0 градусов, но меньше 90 градусов.
Тупой угол больше 90 градусов, но меньше 180 градусов.
Основная литература
- Никольский С. М. Математика. 6 класс: Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н.Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е.Ф. Шершнёв, О.Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И.Ф. Задачи на смекалку: 5-6 кл. // И.Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Диаграмма в переводе с греческого языка – это изображение, рисунок или чертёж.
Круговые диаграммы – позволяют наглядно показывать соотношение целого и его частей.
Рассмотрим круговую диаграмму на примере:
В 8А классе 32 ученика, из них 16 – девочек и 16 – мальчиков.
В 8Б классе 30 учеников, из них 12 – девочек и 18 – мальчиков.
Разберём подробнее диаграмму 8Б.
Все ученики 8Б – это весь круг.
Круг разбит на равные части по числу ребят, так что каждой девочке и каждому мальчику соответствует один угол с вершиной в центре круга (такие углы называются центральными углами).
Для построения круговой диаграммы:
Выясняем, сколько градусов приходится на одну часть.
Имеем две группы учащихся:
12 учащихся класса – девочки.
18 учащихся класса – мальчики.
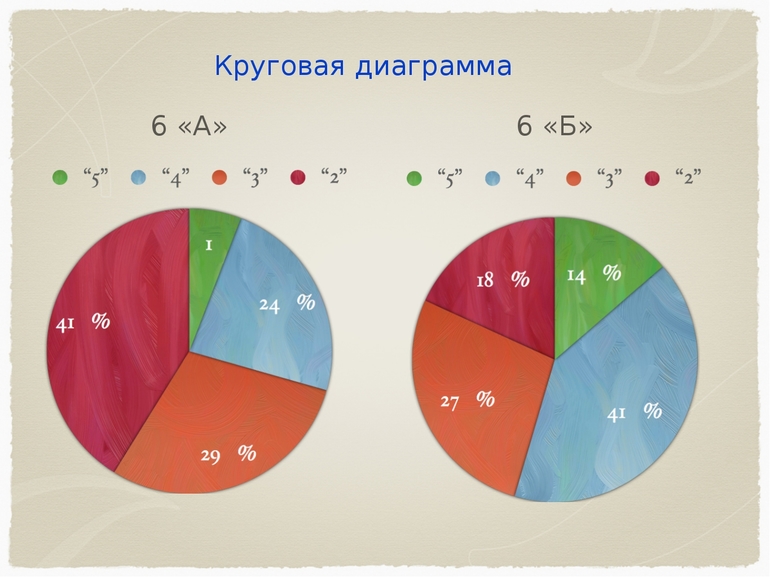
Покажем на круговой диаграмме результаты выполнения контрольной работы по алгебре в 9В классе.
Оценка «5» – 5 человек;
Оценка «4» – 10 человек:
Оценка «3» – 7 человек;
Оценка «2» – 2 человека.
Всего писали контрольную работу:
На диаграмме отражено количество жителей города, имеющих домашних питомцев:
70 % жителей – не содержат домашних питомцев;
30 % жителей – содержат домашних питомцев.
Чтобы построить такую диаграмму, надо определить величину центрального угла, соответствующего 30 и 70 % жителей.
Круговые диаграммы хорошо использовать при небольшом количестве частей, необходимых к изображению на диаграмме. Желательно не использовать круговые диаграммы для изображения более чем 15 различных совокупностей, так как при таком их количестве наглядность преподносимой информации может сильно снижаться.
Разбор заданий тренировочного модуля
№ 1. Единичный выбор.
Выберите верный ответ.
В голосовании должно было принять участите 120 работников предприятия. Используя круговую диаграмму, определите, сколько человек не участвовало в голосовании.
Варианты ответов: 12, 120, 24, 60.
Решение.
Пусть х человек не участвовали в голосовании. На диаграмме оранжевым цветом отмечен соответствующий им центральный угол, и сделана соответствующая их количеству в процентах подпись.
№ 2. Подчеркивания элементов.
Подчеркните верное утверждение.
Градусная мера углов.