Как найти угол в прямоугольном треугольнике формула - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти углы прямоугольного треугольника

Главная
/
Математика
/
Геометрия
/
Как найти углы прямоугольного треугольника

Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

для угла α:

угол β
длины катетов a и b
длину гипотенузы (с) и длину одного из катетов

для угла β:

угол α
длины катетов a и b
длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Если ∠β = , то ∠α =

Если ∠α = , то ∠β =

Формула

α = 90° — β

β = 90° — α

Найти углы прямоугольного треугольника зная катеты

Катет a =
Катет b =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?

Формулы

или так:

α = arctg(^a/_b)

β = arctg(^b/_a)

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°

∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°

Найти углы прямоугольного треугольника по катету и гипотенузе

Гипотенуза c =
Катет =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?

Формулы

sin(α) = ^a/_c

sin(β) = ^b/_c

cos(α) = ^b/_c

cos(β) = ^a/_c

или так:

α = arcsin(^a/_c) = arccos(^b/_c)

β = arcsin(^b/_c) = arccos(^a/_c)

Пример

Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:

∠α = arccos(3/6) = arccos(0.5) = 60°

∠β = arcsin(3/6) = arcsin(0.5) = 30°

См. также

Источник

Укажите размеры:

Результат:

Решение:

Ссылка на страницу с результатом:

# Теория

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

β
α

a
b
c

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

tg alpha = dfrac{a}{b}

tg α — тангенс угла α
a — противолежащий катет
b — прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x. Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

angle alpha + angle beta + angle gamma = 180°

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

angle alpha = 90° — angle beta

angle beta = 90° — angle alpha

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла — острые.

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол A обозначается соответствующей греческой буквой alpha .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла alpha , называется противолежащим (по отношению к углу alpha ). Другой катет , который лежит на одной из сторон угла alpha , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

sin A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle c}.$

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

cos A $=genfrac{}{}{}{0}{displaystyle b}{displaystyle c}.$

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

tg A $=genfrac{}{}{}{0}{displaystyle a}{displaystyle b}.$

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

tg A $=genfrac{}{}{}{0}{displaystyle sin A}{displaystyle cos A}.$

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

ctg A $=genfrac{}{}{}{0}{displaystyle cos A}{displaystyle sin A}.$

Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

sin $displaystyle alpha = frac{a}{c}$	sin ${}^2 alpha +$ cos $displaystyle {}^2 alpha =1$	$alpha + beta = 90 ^{circ}$
cos $displaystyle alpha = frac{b}{c}$	1+tg $displaystyle {}^2 alpha =frac{1}{cos ^2 alpha}$	cos = sin
tg $displaystyle alpha = frac{a}{b}$	1+ctg $displaystyle {}^2 alpha =frac{1}{sin ^2 alpha}$	sin = cos
ctg $displaystyle alpha = frac{b}{a}$		tg = ctg

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна $180^{circ}$ . Значит, сумма двух острых углов прямоугольного треугольника равнa $90^{circ}$ .
С одной стороны, $sin A =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ как отношение противолежащего катета к гипотенузе. С другой стороны, $cos B =genfrac{}{}{}{0}{displaystyle a}{displaystyle c}$ , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, $cos left( 90^{circ}-A right) = sin A$ .
Возьмем теорему Пифагора: . Поделим обе части на получаем $displaystyle left ( frac{a}{c} right )^2+left ( frac{b}{c} right )^2=left ( frac{c}{c} right )^2 ,$ то есть
Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на , получим: $1+tg ^2 A = genfrac{}{}{}{0}{displaystyle 1}{displaystyle cos ^2 A }.$ Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично, $1+ctg ^2 A =genfrac{}{}{}{0}{1}{sin ^2 A }.$

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна $180^{circ}$ .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от $0^{circ}$ до $90^{circ}$ .

	0	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 4}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle pi}{displaystyle 2}$
sin	0	$displaystyle frac{1}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{sqrt{3}}{2}$
cos		$displaystyle frac{sqrt{3}}{2}$	$displaystyle frac{sqrt{2}}{2}$	$displaystyle frac{1}{2}$	0
tg	0	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$			−
ctg	−			$genfrac{}{}{}{0}{displaystyle 1}{displaystyle sqrt{3}}$	0

Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Докажем теорему:

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и C_1 и равными острыми углами А и A_1.

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому $displaystyle frac{AB}{A_1 B_1}=frac{BC}{B_1 C_1}=frac{AC}{A_1 C_1 } .$

Из этих равенств следует, что $displaystyle frac{BC}{AB}=frac{B_1 C_1}{A_1 B_1} ,$ т. е. sin А = sin A_1.

Аналогично, $displaystyle frac{AC}{AB}=frac{A_1C_1}{A_1 B_1},$ т. е. cos А = cos A_1, и $displaystyle frac{BC}{AC}=frac{B_1C_1}{A_1 C_1},$ т. е. tg A = tg A_1.

Это значит, что синус, косинус и тангенс зависят только от величины угла.

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Задача 1. В треугольнике ABC угол C равен $90^{circ}$ , sin A = 0,1. Найдите cos B.

Задача решается за четыре секунды.

Поскольку $A+B = 90^{circ}$ , sin A = cos B = 0,1.

Задача 2. В треугольнике ABC угол равен $90^{circ}$ , AB=5 , $sin A = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}$ .

Найдите .

Решение:

$sin A = genfrac{}{}{}{0}{displaystyle a}{displaystyle c} = genfrac{}{}{}{0}{displaystyle BC}{displaystyle AB} = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25}.$

Отсюда

$BC= genfrac{}{}{}{0}{displaystyle 7}{displaystyle 25} cdot AB = genfrac{}{}{}{0}{displaystyle 7}{displaystyle 5}.$

Найдем AC по теореме Пифагора.

$AC=sqrt{AB^2-BC^2} = genfrac{}{}{}{0}{displaystyle 24}{displaystyle 5} = 4,8.$

Ответ: 4,8.

Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.

Решение:

Для угла А противолежащий катет – это ВС,

АВ является гипотенузой треугольника, лежит против Значит, sin A $displaystyle = frac{BC}{AB}= frac{5}{13}.$

Катет, прилежащий к angle A – это катет АС, следовательно, cos⁡ А $displaystyle = frac{AC}{AB}=frac{AC}{13}.$

Длину катета АС найдем по теореме Пифагора:

Тогда $AC = sqrt{AB^2-BC^2}=sqrt{(13)^2-5^2}=sqrt{144}=12.$

cos⁡ А $displaystyle = frac{12}{13}=0,923 ... approx 0,92 ;$

tg A $displaystyle = frac{BC}{AC} = frac{5}{12}=0,416...approx 0,42.$

Ответ: 0,92; 0,42.

Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.

Задача 4. В треугольнике АВС угол С равен AC = 2, sin A= $displaystyle frac{sqrt{17}}{17} .$

Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.

Так как sin A $displaystyle = frac{a}{c} = frac{BC}{AB} = frac{sqrt{17}}{17},$ $displaystyle frac{a}{c} = frac{sqrt{17}}{17} ,$ $displaystyle c = frac{17a}{sqrt{17}}=sqrt{17}a.$

По теореме Пифагора получим

$a^2+2^2=(sqrt{17} a)^2;$

$displaystyle a= frac{1}{2}=0,5;$

Ответ: 0,5.

Задача 5. В треугольнике АВС угол С равен AC = 4, tg A = $displaystyle frac{33}{4sqrt{33}} .$ Найдите AB.

Решение:

AC = b = 4, tg A $displaystyle = frac{a}{b}=frac{33}{4sqrt{33}},$

$displaystyle frac{a}{4}=frac{33}{4sqrt{33}},$ $displaystyle a=frac{4 cdot 33}{4 cdot sqrt{33}}=sqrt{33},$

$AB = c = sqrt{a^2+b^2}=sqrt{(sqrt{33})^2+4^2}=sqrt{33+16} =7.$

Ответ: 7.

Задача 6.

В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = $displaystyle frac{1}{5} .$ Найдите AH.

Решение:

AВ = с = 13, tg A = $displaystyle frac{a}{b}=frac{1}{5} ,$ тогда b = 5a.

По теореме Пифагора ABC:

$displaystyle a=sqrt{frac{169}{26}}=frac{13}{sqrt{26}},$ тогда $displaystyle b = 5a=5cdot frac{13}{sqrt{26}}=frac{65}{sqrt{26}}.$

(по двум углам), следовательно $displaystyle frac{AH}{AC}=frac{AC}{AB} ,$ откуда

$displaystyle AH = frac{AC^2}{AB}=frac{b^2}{c}=left ( frac{65}{sqrt{26}}right )^2:13=12,5.$

Ответ: 12,5.

Задача 7. В треугольнике АВС угол С равен

CH – высота, BC = 3, sin A = $displaystyle frac{1}{6} .$

Найдите AH.

Решение:

Так как sin A = $displaystyle frac{a}{c} = frac{BC}{AB} = frac{1}{6},$ тогда $displaystyle frac{3}{c} = frac{1}{6} ,$ c = АВ = 18.

sin A = $displaystyle frac{a}{c}$ = cos⁡ B = $displaystyle frac{1}{6} .$

Рассмотрим BHC:

${cos B= }displaystyle frac{BH}{BC}$ = $displaystyle frac{1}{6} ,$ получим $displaystyle frac{BH}{3}=displaystyle frac{1}{6},$

тогда BH = $displaystyle frac{3}{6}=displaystyle frac{1}{2}$ = 0,5,

AH = AB — BH = 18 — 0,5 = 17,5.

Ответ: 17,5.

Задача 8. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BC = 3, cos A = $displaystyle frac{sqrt{35}}{6}.$

Найдите АH.

Решение:

Так как для АВС: cos A = $displaystyle frac{AC}{AB}=$ sin В = $displaystyle frac{sqrt{35}}{6},$

а для ВНС: sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{sqrt{35}}{6}$ , откуда СН = $displaystyle frac{BC cdot sqrt{35}}{6}=displaystyle frac{3 cdot sqrt{35}}{6}=displaystyle frac{sqrt{35}}{2},$

По теореме Пифагора найдем ВН:

$BH = sqrt{{BC}^2-{CH}^2}=sqrt{3^2-{left(displaystyle frac{sqrt{35}}{2}right)}^2}=$

$=sqrt{9-displaystyle frac{35}{4}}=sqrt{displaystyle frac{1}{4}}=displaystyle frac{1}{2}=0,5.$

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:

${CH}^2=AH cdot BH,$ тогда $AH= displaystyle frac{ {CH}^2}{BH}, ; AH= displaystyle frac{ {left(displaystyle frac{sqrt{35}}{2}right)}^2}{0,5}=displaystyle frac{35 cdot 2}{4}=17,5.$

Ответ: 17,5.

Задача 9. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:

По определению sin A= $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ =

Рассмотрим BHC : ${cos B= }displaystyle frac{BH}{BC}.$

ВС найдем по теореме Пифагора:

ВС= $sqrt{{BH}^2+{CH}^2}=sqrt{7^2+{24}^2}=sqrt{49+576}=sqrt{625}=25,$

тогда ${cos B= }displaystyle frac{BH}{BC}=displaystyle frac{7}{25}=0,28,$ а значит и sin A = = 0,28.

Ответ: 0,28.

Задача 10. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:

По определению sin A = $displaystyle frac{a}{c}$ = $displaystyle frac{BC}{AB}$ = cos A = $displaystyle frac{b}{c}$ = $displaystyle frac{AC}{AB}$ =

тогда tg A = $displaystyle frac{sin A}{{cos A }}=displaystyle frac{cosB}{sinB}=ctgB,$ который найдем из BHC:

$ctgB=displaystyle frac{BH}{CH}=displaystyle frac{4}{8}=0,5.$

Ответ: 0,5.

Задача 11. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, tg A = $displaystyle frac{2}{3}.$ Найдите АН.

Решение:

По определению tg A= $displaystyle frac{BC}{AC}=ctgB=displaystyle frac{2}{3}.$

Для BHC: $ctgB=displaystyle frac{BH}{CH}=displaystyle frac{2}{3}$ , значит $displaystyle frac{12}{CH}=displaystyle frac{2}{3},$ СН = $displaystyle frac{12 cdot 3}{2}=18.$

Для АHC: tg A= $displaystyle frac{CH}{AH}=displaystyle frac{2}{3},$ то $displaystyle frac{18}{AH}=displaystyle frac{2}{3},$ AH = $displaystyle frac{18 cdot 3}{2}=27.$

Ответ: 27.

Задача 12. В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, BН = 12, sin A = $displaystyle frac{2}{3}.$ Найдите АВ.

Решение:

Так как cos В = $displaystyle frac{BC}{AB}$ = sin A = $displaystyle frac{2}{3}.$

Из СВН имеем cos В = $displaystyle frac{HB}{BC}$ = $displaystyle frac{2}{3},$ тогда ВС = $displaystyle frac{3 cdot HB}{2}=displaystyle frac{3 cdot 12}{2}=18.$

В АВС имеем sinA = $displaystyle frac{BC}{AB}$ = $displaystyle frac{2}{3},$ тогда AВ = $displaystyle frac{3 cdot BC}{2}=displaystyle frac{3 cdot 18}{2}=27.$

Ответ: 27.

Задача 13. В треугольнике АВС угол С равен 90 ${}^circ,$ из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.

Решение:

Найдем НВ по теореме Пифагора из ВСН:

$HB = sqrt{BC^2-BH^2}=sqrt{20^2-12^2}=sqrt{(20-12)(20+12)}=$

sin В = $displaystyle frac{CH}{BC}$ = $displaystyle frac{12}{20}=displaystyle frac{3}{5}.$

Для АВС: cos A = $displaystyle frac{AC}{AB}=sin B=displaystyle frac{3}{5},$ получили cos A = 0,6.

Найдем АС и АВ несколькими способами.

1-й способ.

Так как cos A = $displaystyle frac{AC}{AB}=displaystyle frac{3}{5},$ то пусть АС = 3х, АВ = 5х,

тогда по теореме Пифагора ${AC}^2+{BC}^2= {AB}^2,$ получим ${(3x)}^2+{(20)}^2= {(5x)}^2$
${25x}^2-{9x}^2= {20}^2 ,$

${16x}^2= {20}^2,$

$x^2= {left(displaystyle frac{20}{4}right)}^2,$
х = 5 ( так как х0). Значит,

2-й способ.

(по двум углам), значит $displaystyle frac{HB}{CB}=frac{HC}{AC}=frac{BC}{AB}$ или $displaystyle frac{16}{20}={12}{AC}={20}{AB} = k,$

k = $displaystyle frac{16}{20}=displaystyle frac{4}{5} ,$ тогда $displaystyle frac{12}{AC}=displaystyle frac{4}{5},$ АС = $displaystyle frac{12 cdot 5}{4}=15$ ; $displaystyle frac{20}{AB}=displaystyle frac{4}{5},$ АВ = $displaystyle frac{20 cdot 5}{4}=25.$

3-й способ.

${CH}^2=AH cdot HB$ (высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда ${12}^2=AH cdot 16,$ АН = 144:16 = 9.

АВ = АН + НВ = 9 + 16 = 25.

По теореме Пифагора найдем АС:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{25}^2-{20}^2}=sqrt{(25-20)(25+20)}$ =

Ответ: cos A = 0,6; АС = 15, АВ = 25.

Задача 14.

Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.

Найдите АВ и cos А.

Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:

ВС = $sqrt{{HC}^2+{BH}^2}=sqrt{{18}^2+{24}^2}=sqrt{324+576}$ =

cos C = $displaystyle frac{HC}{BC}=displaystyle frac{18}{30}=displaystyle frac{3}{5}.$

Для АВС: sin А = $displaystyle frac{BC}{AC}$ = cos C = $displaystyle frac{3}{5}.$

Для АНВ: sin А = $displaystyle frac{BH}{AB}$ = $displaystyle frac{3}{5},$ то $displaystyle frac{24}{AB}$ = $displaystyle frac{3}{5},$ АВ = $displaystyle frac{24 cdot 5}{3}=40.$

Из основного тригонометрического тождества найдем

cos A = $sqrt{1-{sin}^2A}=sqrt{1-0,36}=sqrt{0,64}=0,8.$

Ответ: АВ = 40, cos A = 0,8.

Задача 15.

Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А = $displaystyle frac{7}{25}.$

Найдите площадь треугольника.

Решение:

В прямоугольном АСЕ sin А = $displaystyle frac{CE}{AC},$

значит $displaystyle frac{7}{25}$ = 14.

Второй катет найдем, используя теорему Пифагора: $AE= sqrt{{AC}^2-{CE}^2};$

$AE = sqrt{{50}^2-{14}^2}=sqrt{(50-14)(50+14)} =sqrt{36cdot 64}=6cdot8=48.$

Площадь прямоугольного треугольника равна S = $displaystyle frac{1}{2}ab,$

поэтому $S_{ACE}= displaystyle frac{1}{2} AEcdot CE=displaystyle frac{48cdot 14}{2}=336.$

Ответ: 336.

Задача 16.

В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.

Найдите sin Результат округлите до сотых.

Решение:

A-общий, $angle AKC=angle ACB=90{}^circ$ ),

значит sin $angle ACK=displaystyle frac{AK}{AC}=displaystyle frac{AC}{AB}.$

Найдем АС по теореме Пифагора из САВ:

$AC = sqrt{{AB}^2-{BC}^2}=sqrt{{13}^2-{12}^2}=$

Тогда sin $angle ACK=displaystyle frac{5}{13}=0,384..approx 0,38.$

Ответ: 0,38.

Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = $displaystyle frac{12}{13}.$ Найдите высоту СН.

Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда

высота СН является медианой, то есть АН = НВ = $displaystyle frac{1}{2}AB=36.$

Поскольку АСН — прямоугольный,

cos A = $displaystyle frac{AH}{AC}=$ $displaystyle frac{12}{13},$ то есть $displaystyle frac{36}{AC}=$ $displaystyle frac{12}{13}$ АС = $displaystyle frac{36 cdot 13}{12}=39.$

По теореме Пифагора ${AH}^2+{CH}^2={AC}^2,$ тогда

$CH = sqrt{{AC}^2-{AH}^2} = sqrt{{39}^2-{36}^2}=$

Ответ: 15.

Задача 18. В треугольнике АВС угол С равен 90 ${}^circ,$ sin A = $displaystyle frac{11}{14},$ AC = 10 Найдите АВ.

Решение:

1-й способ.

Поскольку sin A = $displaystyle frac{BC}{AB}=$ $displaystyle frac{11}{14},$ то можно обозначить

ВС = 11х, АВ = 14х.

По теореме Пифагора $AC^2+{BC}^2={AB}^2;$

${(10sqrt{3})}^2+{(11x)}^2={(14x)}^2;$

${(14x)}^2-{(11x)}^2 = 3 cdot 100;$

(14х- 11х)(14х + 11х) = 3 cdot 100;

x^2=4, учитывая, что длина стороны положительна, х = 2,

следовательно, АВ = 14 cdot 2 = 28.

2-й способ.

Воспользуемся основным тригонометрическим тождеством ${sin}^2A+{cos}^2A=1;$

cos A = $sqrt{1-{sin}^2A}=sqrt{1-{left(displaystyle frac{11}{14}right)}^2}=sqrt{displaystyle frac{196-121}{196}}=sqrt{displaystyle frac{75}{196}}=displaystyle frac{5sqrt{3}}{14}.$

По определению cos A = $displaystyle frac{AC}{AB},$ значит $displaystyle frac{AC}{AB}= displaystyle frac{5sqrt{3}}{14}.$

Так как АС=10 то $displaystyle frac{10sqrt{3}}{AB}= displaystyle frac{5sqrt{3}}{14},$ откуда АВ = $displaystyle frac{10sqrt{3} cdot 14}{5sqrt{3}}$ = 28.

Ответ: 28.

Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 sqrt{3} и 4.

Решение:

Пусть angle ВАО = alpha .

Диагонали ромба делят его углы пополам, значит, = alpha .

Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = $displaystyle frac{1}{2} AC=2sqrt{3},$ а катет ВО = $displaystyle frac{1}{2}BD =2.$

Поэтому tg $alpha =displaystyle frac{BO}{AO}=displaystyle frac{2}{2sqrt{3}}=displaystyle frac{1}{sqrt{3}},$ откуда $alpha =30{}^circ .$

$angle BAD=2alpha =60{}^circ , ; angle ADC=angle ABC=180{}^circ -60{}^circ =120{}^circ .$

Ответ: ${60}^circ,$ ${120}^circ,$ ${60}^circ,$ ${120}^circ .$

Часто в задачах встречаются треугольники с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ или с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами $90^{circ},, 30^{circ}$ и $60^{circ}$ катет, лежащий напротив угла в $30^{circ}$ , равен половине гипотенузы.

Треугольник с углами $90^{circ},, 45^{circ}$ и $45^{circ}$ — равнобедренный. В нем гипотенуза в sqrt{2} раз больше катета.

Задача 20.

В треугольнике АВС угол С равен 90 ${}^circ,$ угол А равен 30 ${}^circ,$ АВ = 2

Найдите высоту CH.

Решение:

Рассмотрим АВС:

По свойству катета, лежащего против угла ${30}^circ,$ имеем ВС = $displaystyle frac{1}{2}$ АВ =

В BHC: $angle BHC=90{}^circ ,; angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно, ВН = $displaystyle frac{1}{2}$ BC = $displaystyle frac{sqrt{3}}{2}.$

По теореме Пифагора найдем НС:

$HC = sqrt{{BC}^2-{BH}^2}=sqrt{{left(sqrt{3}right)}^2-{left(displaystyle frac{sqrt{3}}{2}right)}^2}=sqrt{3-displaystyle frac{3}{4}}=$

$=sqrt{2displaystyle frac{1}{4}}=sqrt{displaystyle frac{9}{4}}=displaystyle frac{3}{2}=1,5.$

Ответ: 1,5.

Задача 21.

В треугольнике АВС угол С равен 90 ${}^circ,$ CH — высота, АВ = 2, $angle A=30{}^circ .$ Найдите АH.

Решение:

Из АВС найдем ВС = $displaystyle frac{1}{2}$ АВ = 1 (по свойству катета, лежащего против угла 30 ${}^circ$ ),

$angle A=30{}^circ ,$ то $angle B=60{}^circ .$

Из ВСН: $angle BHC=90{}^circ , angle B=60{}^circ ,$ то $angle HCB=30{}^circ ,$ следовательно,

ВН = $displaystyle frac{1}{2}$ ВС = $displaystyle frac{1}{2}.$

АН = АВ — НВ = 2 — $displaystyle frac{1}{2}$ = 1,5.

Ответ: 1,5.

Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Triangles are three-sided closed polygons formed by the intersection of three lines. It is encountered a lot in everyday life. It is one of the basic shapes of geometry. It has three sides, three angles, and three vertices. A Right Angled Triangle is one where one of the angles is always equal to 90°. Pythagoras Theorem is derived for Right-angled triangles, Which states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of base and perpendicular.

Given the length of at least two sides of a Right-Angled triangle, we can find the value of any angle of the right-angled triangle. For this, we use various trigonometric functions like sine, cosine, tangent, cotangent, sec, and cosec. These help us to relate the angles of a right-angled triangle with its sides.

Properties

There is a right-angle vertex among the three vertices
The side opposite to the right-angled vertex is called the hypotenuse.
The length of the sides follows the Pythagoras theorem, which states

hypotenuse² = base² + altitude²

The hypotenuse is the longest side of a right-angled triangle.
The angles other than the right angle are acute angles since the value is less than 90^o

Trigonometric functions

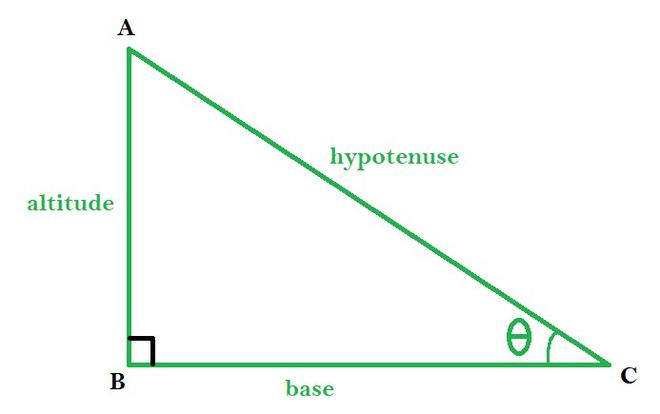
ABC is a right-angled triangle with ∠B as right-angle

cosθ: This gives the ratio of the base by the hypotenuse of a right-angled triangle.

cosθ = base / hypotenuse

sinθ: This gives the ratio of altitude by the hypotenuse of a right-angled triangle.

sinθ = altitude / hypotenuse

tanθ: It is the ratio of altitude by the base of a right-angled triangle.

tanθ = altitude / base

cotθ: It is the inverse of tanθ
secθ: It is the inverse of cosθ
cosecθ: It is the inverse of sinθ

To find the angles of a right-angled triangle, we can take the trigonometric inverse of the ratio of given sides of the triangle.

Example:

If sinθ = x, then we can write

θ = sin^-1x.

This returns the angle for which the sine value of the angle is x.

Similarly, there exists cos^-1θ, tan^-1θ, cot^-1θ, sec^-1θ, and cosec^-1θ

Sample Problems

Question 1. Given a right-angled triangle, with base equals 10cm and hypotenuse equals 20cm. Find the value of the base angle.

Solution:

Given, Base = 10cm

Hypotenuse = 20cm

Let, the value of the base angle be θ. We can write

cosθ = base / hypotenuse = 10/20 = 1/2

θ = cos^-1(1/2) = 60^o

Thus, the value of base angle is 60^o.

Question 2. Find the value of angles of a right angles triangle, given that one of the acute angles is twice the other.

Solution:

Since we know the sum of all the three angles in a triangle is 180^o.

Since one of the angles is 90^o and one of the acute angles is twice the other, we can consider them as θ and 2θ.

So, we can write

90^o + θ + 2θ = 180^o

3θ = 180^o – 90^o

3θ = 90^o

θ = 90^o/3 = 30^o

2θ = 2 × 30^o = 60^o

So, the angles are 30^o, 60^o, and 90^o.

Question 3. Find the value of the angle of elevation of a ladder of length 5m, given that base of the ladder is at a distance of 3m from the wall.

Solution:

Since the ladder acts as a hypotenuse of a right angles triangle and base distance equals 3m, we can write

Hypotenuse = 5m

Base = 3m

Let the angle of elevation be θ. So, we can write

cosθ = Base / Hypotenuse = 3/5

θ = cos^-1(3/5)

θ = 53^o

Thus, the value of the angle of elevation is 53^o.

Question 4. Find the value of hypotenuse, given the length of the altitude is 8m and the base angle equals 30^o.

Solution:

Given, the base angle is equal to 30^o and altitude equals 8m, we can apply the sine function to find the length of the hypotenuse.

sin30^o = altitude / hypotenuse

hypotenuse = altitude / sin30^o

Since the value of sin30^o equals 1/2, we can write

hypotenuse = altitude / (1/2) = 2 × altitude

Thus, hypotenuse = 2 × 8 = 16m

Thus, the length of the hypotenuse is equal to 16m.

Last Updated :
18 Aug, 2022

Like Article

Save Article

Источник

Как найти углы прямоугольного треугольника

Онлайн калькулятор

Найти угол α зная угол β и наоборот

Формула

Найти углы прямоугольного треугольника зная катеты

Формулы

Пример

Найти углы прямоугольного треугольника по катету и гипотенузе

Формулы

Пример

См. также

Формула тангенса

Углы треугольника

Похожие калькуляторы:

Синус, косинус и тангенс острого угла прямоугольного треугольника

Sample Problems