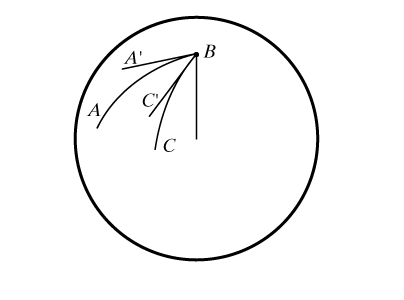Как найти угол в сфере

• Главная
• Вопросы и ответы

Вычисление угла образованного тремя точками на сфере

Немного геометрии для решения задачи нахождения угла для случая сферы, используемый код может применяться в других расширениях.

Обсудить в форуме Комментариев — 10

Согласно
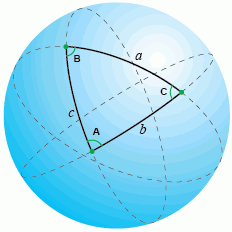
сферической теореме косинусов:
косинус одной стороны сферического треугольника равняется произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними.

Одно из отличий сферического треугольника от обычного заключается в том, что сумма его углов больше 180 градусов.

В уравнениях используются угловые длины в радианах.

Отсюда, зная координаты трех точек и вычислив расстояния между ними по формулам вычисления расстояний на сфере, можно получить любой из трех углов, например угол A:

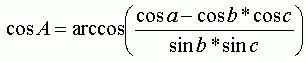
Скачать пример расчета в Excel

Вычислениям приведенным выше соответствует следующий
код на языке Avenue (координаты трех точек и расчеты расстояний передаются отдельно) (скачать скрипт):

'вычисление расстояний по формулам большого круга,
'GreatCirclesDist - название скрипта для вычислений
'расстояний по формулам большого круга в проекте
pnts = {}
pnts = pnts.add(a)
pnts = pnts.add(b)
ab = av.run("GreatCirclesDist", pnts).Get(0)
pnts = {}
pnts = pnts.add(b)
pnts = pnts.add(c)
bc = av.run("GreatCirclesDist", pnts).Get(0)
pnts = {}
pnts = pnts.add(a)
pnts = pnts.add(c)
ca = av.run("GreatCirclesDist", pnts).Get(0)
A = (((a.cos) - (b.cos*c.cos))/b.sin*c.sin).ACos.AsDegrees

Обсудить в форуме Комментариев — 10

Последнее обновление: September 09 2021

Дата создания: 06.06.2006

Автор(ы): Максим Дубинин

СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ – математическая дисциплина, изучающая геометрические образы (точки, линии, фигуры), находящиеся на сфере, и соотношения между ними.

По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355), одного из участников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах. Значительный вклад в сферическую геометрию внес Менелай из Александрии (ок. 100 н.э.). Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея (ок. 150), у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.

Основные положения сферической геометрии.

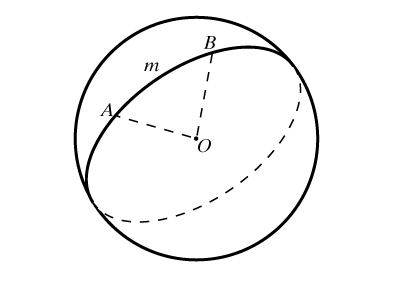
Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит же бесконечное количество больших кругов. Меньшая дуга AmB (рис. 1) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической. Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. И еще один удивительный с точки зрения планиметрии факт – треугольник на сфере может иметь все три прямых угла.

Прямые, отрезки, расстояния и углы на сфере.

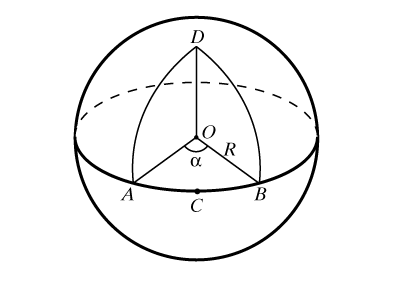
Прямыми на сфере считаются большие окружности. Если две точки принадлежат большой окружности, то длина меньшей из дуг, соединяющих эти точки, определяется как сферическое расстояние между этими точками, а сама дуга – как сферический отрезок. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков – больших полуокружностей. Длина сферического отрезка определяется через радианную меру центрального угла a и радиус сферы R (рис. 2), по формуле длины дуги она равна R a. Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, т.е. РАОС + РСОВ = РАОВ. Для любой же точки D вне отрезка АВ имеет место «сферическое неравенство треугольника»: сумма сферических расстояний от D до А и от D до В больше АВ, т.е. РAOD + РDOB > РAOB, – полное соответствие между сферической и плоской геометриями. Неравенство треугольника – одно из основополагающих в сферической геометрии, из него следует, что, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы.

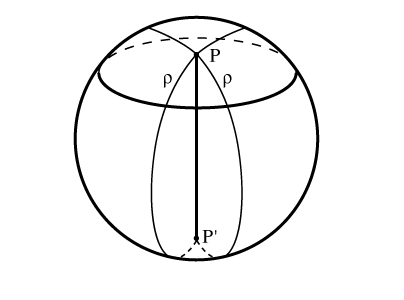
Таким же образом на сферу можно перенести и многие другие понятия планиметрии, в частности те, которые можно выразить через расстояния. Например, сферическая окружность – множество точек сферы, равноудаленных от заданной точки Р. Легко показать, что окружность лежит в плоскости, перпендикулярной диаметру сферы РР` (рис. 3), т.е. это обычная плоская окружность с центром на диаметре РР`. Но сферических центров у нее два: Р и Р`. Эти центры принято называть полюсами. Если обратиться к глобусу, то можно видеть, что идет речь именно о таких окружностях, как параллели, и сферическими центрами всех параллелей являются Северный и Южный полюса. Если диаметр r сферической окружности равен p/2, то сферическая окружность превращается в сферическую прямую. (На глобусе – экватор). В этом случае такую окружность называют полярой каждой из точек Р и P`.

Одним из важнейших понятий в геометрии является равенство фигур. Фигуры считаются равными, если одну на другую можно отобразить таким образом (поворотом и переносом), что сохранятся расстояния. Это верно и для сферической геометрии.

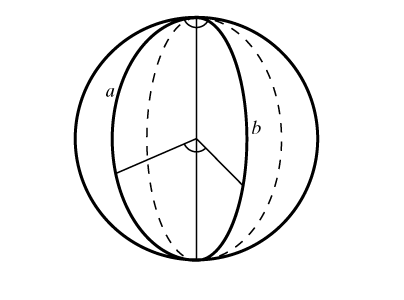
Углы на сфере определяются следующим образом. При пересечении двух сферических прямых a и b на сфере образуются четыре сферических двуугольника, подобно тому, как две пересекающиеся прямые на плоскости разбивают ее на четыре плоских угла (рис. 4). Каждому из двуугольников соответствует двугранный угол, образованный диаметральными плоскостями, содержащими a и b. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.

Отметим так же, что угол РABC, образованный на сфере двумя дугами большого круга, измеряют углом РA`BC` между касательными к соответствующим дугам в точке В (рис. 5) или двугранным углом, образованным диаметральными плоскостями, содержащими сферические отрезки АВ и ВС.

Точно так же, как и в стереометрии, каждой точке сферы сопоставляется луч, проведенный из центра сферы в эту точку, а любой фигуре на сфере – объединение всех пересекающих ее лучей. Так, сферической прямой соответствует содержащая ее диаметральная плоскость, сферическому отрезку – плоский угол, двуугольнику – двугранный угол, сферической окружности – коническая поверхность, ось которой проходит через полюсы окружности.

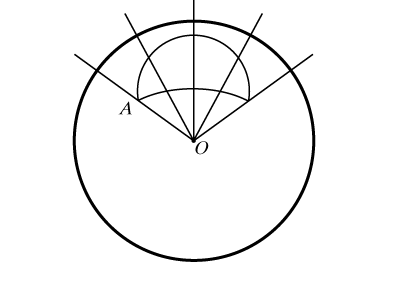
Многогранный угол с вершиной в центре сферы пересекает сферу по сферическому многоугольнику (рис. 6). Это область на сфере, ограниченная ломаной из сферических отрезков. Звенья ломаной – стороны сферического многоугольника. Их длины равны величинам соответствующих плоских углов многогранного угла, а величина угла при любой вершине А равна величине двугранного угла при ребре ОА.

Сферический треугольник.

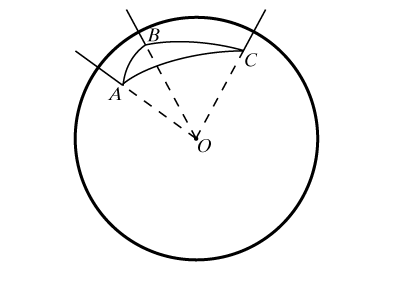
Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла (рис. 7).

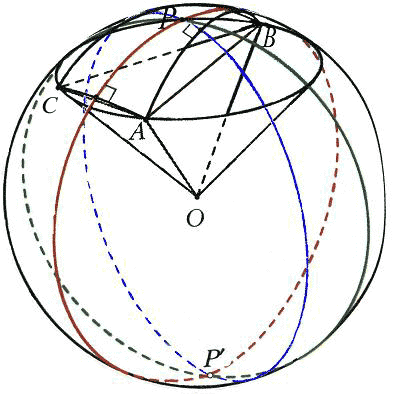
Многие свойства сферического треугольника (а они одновременно являются и свойствами трехгранных углов) почти полностью повторяют свойства обычного треугольника. Среди них – неравенство треугольника, которое на языке трехгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других. Или, например, три признака равенства треугольников. Все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудаленных от концов отрезка, будет и на сфере перпендикулярной к нему прямой, проходящей через его середину, откуда следует, что серединные перпендикуляры к сторонам сферического треугольника AВС имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р`, являющиеся полюсами его единственной описанной окружности (рис. 8). В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.

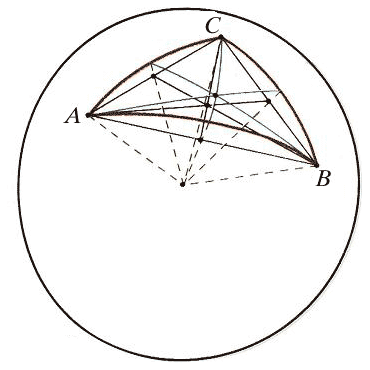
Теоремы о пересечении высот и медиан также остаются верными, но их обычные доказательства в планиметрии прямо или косвенно используют параллельность, которой, на сфере нет, и потому проще доказать их заново, на языке стереометрии. Рис. 9 иллюстрирует доказательство сферической теоремы о медианах: плоскости, содержащие медианы сферического треугольника АВС, пересекают плоский треугольник с теми же вершинами по его обычным медианам, следовательно, все они содержат радиус сферы, проходящий через точку пересечения плоских медиан. Конец радиуса и будет общей точкой трех «сферических» медиан.

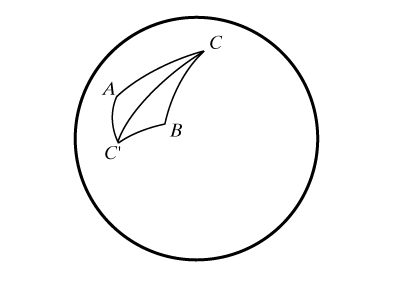
Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` (рис. 10).

Сумма углов всякого сферического треугольника всегда больше 180°. Разность РА+РВ +РС – p = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.

Если рассматривать двуугольник с углом a, то при 226 = 2p/n (n – целое число) сферу можно разрезать ровно на п копий такого двуугольника, а площадь сферы равна 4пR² = 4p при R = 1, поэтому площадь двуугольника равна 4p/n = 2a. Эта формула верна и при a = 2pт/п и, следовательно, верна для всех a. Если продолжить стороны сферического треугольника АВС и выразить площадь сферы через площади образующихся при этом двуугольников с углами А, В, С и его собственную площадь, то можно прийти к вышеприведенной формуле Жирара.

Координаты на сфере.

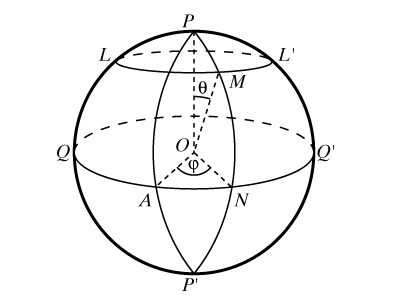
Каждая точка на сфере вполне определяется заданием двух чисел; эти числа (координаты) определяются следующим образом (рис. 11). Фиксируется некоторый большой круг QQ` (экватор), одна из двух точек пересечения диаметра сферы PP`, перпендикулярного к плоскости экватора, с поверхностью сферы, например Р (полюс), и один из больших полукругов PAP`, выходящих из полюса (первый меридиан). Большие полукруги, выходящие из P, называются меридианами, малые круги, параллельные экватору, такие, как LL`, – параллелями. В качестве одной из координат точки M на сфере принимается угол q = POM (высота точки), в качестве второй – угол j = AON между первым меридианом и меридианом, проходящим через точку M (долгота точки, отсчитываемая против часовой стрелки).

В географии (на глобусе) в качестве первого меридиана принято использовать Гринвичский меридиан, проходящий через главный зал Гринвичской обсерватории (Гринвич – городской округ Лондона), он разделяет Землю на Восточное и Западное полушария, соответственно и долгота бывает восточной либо западной и измеряется от 0 до 180° в обе стороны от Гринвича. А вместо высоты точки в географии принято использовать широту, т.е. угол NOM = 90° – q, отсчитываемый от экватора. Т.к. экватор делит Землю на Северное и Южное полушария, то и широта бывает северной либо южной и изменяется от 0 до 90°.

Марина Федосова

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

Государственное образовательное учреждение
высшего

Профессионального образования

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

ОБЛАСТНОЙ УНИВЕРСИТЕТ (МГОУ)

Кафедра высшей алгебры, элементарной
математики и методики преподавания математики

­­­­­­

Основы структур алгебры

тема: Элементы сферической геометрии

                                         
Выполнила

                                                      
Луценко Евгения Сергеевна

Научный руководитель:

Кандидат педагогических наук

Федяев Олег Ипполитович

Москва

2015

Содержание

Введение

1.Основные
понятия сферической геометрии…………………..4-9

2.Сферическии
треугольник……………………………………..9-13

3.Сферическая
теорема синусов…………………………………13-15

4.Сферическая
теорема косинусов………………………………16-19

5.Решение
сферических треугольников…………………………19-22

6.Примеры решения задач………………………………….22-25

Заключение……………………………………………………26

Список
литературы ………………………………………………..27

Введение

В настоящее время,
существуют различные науки, в основе которых лежит сферическая геометрия.
Например, значительный раздел математической картографии —
картометрия, которая позволяет по данным карты измерять расстояния, углы и
площади на реальной поверхности Земли.

В программе школьного курса геометрии изучению сферы отводится очень
мало времени, при этом рассматриваются только основные понятия, и совсем не
уделяется внимание фигурам на сфере.

Еще
древние греки считали окружность (круг) и сферу (шар) идеальными формами. Форму шара имеет наша планета и большинство космических тел. А так как
планеты, Солнце, Луна и звёзды движутся по воображаемой «небесной сфере», то
естественно, для изучения их движения потребовалось знание геометрии сферы.

     Курсовая работа состоит из двух
частей: в первой приводится общая теория о сфере, понятие сферического
треугольника, сферические теоремы синусов и косинусов, двойственная теорема
косинусов.

Во второй части работы я рассмотрела решения задач на
применение рассмотренных теорем, а также задачи практического характера.

Теоретический материал представлен в форме
доступной для понимания учащимися старших классов, подобраны и решены задачи по
сферической геометрии.

Основные
понятия сферической геометрии

Сфера, большая и малая окружности.

Сферой
называется геометрическое место точек пространства, расположенных на данном
расстоянии от данной точки, называемой её центром.

Отрезок, соединяющий центр сферы с какой-либо его точкой,
называется радиусом сферы.

Отрезок, соединяющий две точки сферы и проходящий, кроме
того, через его центр, называется диаметром. Из определения следует, что
все радиусы равны и что диаметр равен удвоенному радиусу.

Плоскость, проходящая через центр сферы, называется диаметральной
плоскостью.

В этом случае окружность на сфере и называется большой
окружностью. В геометрии на сфере большие окружности играют роль прямых на
плоскости.

Так как через всякие три точки пространства, не лежащие на
одной прямой, проходит единственная плоскость, то через всякие две точки
сферы, не являющиеся диаметрально противоположными, проходит единственная
большая окружность (рис.1). Этот факт вполне аналогичен тому, что на
плоскости через всякие две точки проходит единственная прямая. Через две
диаметрально противоположные точки сферы, напротив, можно провести бесконечное
множество больших окружностей (рис.2).

 Так как всякие две диаметральные плоскости сферы
пересекаются по её диаметру, то всякие две большие окружности пересекаются в
двух диаметрально противоположных точках сферы (рис.4). Здесь наблюдается
отличие сферической геометрии от плоской геометрии, в которой две прямые
пересекаются не более чем в одной точке.

Рис
1                                             Рис 2

-Так как плоскость делит пространство
на две области, то большая окружность делит сферу на две области; эти
области называются полусферами, а сама окружность – краем этих
полусфер.

— Так как две пересекающееся плоскости
делят пространство на четыре области, то две большие окружности делят сферу
на четыре области (рис.3).

-Так как три плоскости, пересекающиеся в одной точке, делят
пространство на восемь областей, то три большие окружности, не
пересекающиеся в одной точке,

 делят сферу на восемь областей
(на рис.4)

Рис
3                                                 Рис 4.

Если первые два из этих свойств
аналогичны свойствам прямых на плоскости, которая делится на две области прямой
и на четыре области двумя пересекающимися прямыми, то третье из указанных
свойств не вполне аналогично соответствующему свойству прямых на плоскости, так
как три попарно пересекающиеся прямые, не проходящие все три через одну точку,
делят плоскость не на восемь, а на семь частей (рис.5).

Рис 5.

Сферический отрезок, соединяющий две
точки на сфере— кратчайшая из двух дуг большой окружности (АВ), про­ходящей через
две не диаметрально противоположные точки A и В сферы.

Если две точки сферы А и В не являются диаметрально
противоположными, то существует единственная плоскость, проходящая через центр
сферы и эти две точки. Линия пересечения этой плоскости со сферой есть большая
окружность, а меньшую из двух дуг этой окружности, соединяющий точки    А и В,
является единственным сферическим отрезком, соединяющим точки А и В.

Если точки А и В диаметрально противоположны на сфере,
существует бесконечное число больших окружностей, проходящих через эти две
точки, причем эти две точки делят каждую такую большую окружность на две
полуокружности, которые являются сферическими отрезками, соединяющими точки А и
В (рис.6).

Рис.6

Сферический
отрезок обладает замечательным минимальным свойством (как и отрезок на
плоскости).

Теорема (минимальное свойство сферического
отрезка).

Сферический
отрезок, соединяющий две точки на сфере, короче любой другой линии на сфере,
соединяющий эти две точки (рис.7).

Рис.7

Угол на сфере

Величина внутреннего угла при
вершине В сферического многоугольника, образованного  дугами АВ и ВС на сфере,
определяется как угол между двумя лучами, которые выходят из точки В и касаются
дуг АВ и ВС в точке В. Поскольку эти лучи  перпендикулярны радиусу ОВ, то угол
при вершине В равен двугранному углу между плоскостями ОАВ и ОВС. Понятно, что
два угла сферического двуугольника всегда равны (рис.8).

рис.8

Многоугольники на сфере

Сферическим многоугольником называется часть
сферы, ограниченная дугами больших окружностей, меньшими полуокружности,
концами которых служат точки пересечения этих больших окружностей, взятых в
последовательном порядке.

Сферический многоугольник называется выпуклым, если
он расположен по одну сторону от каждого из больших кругов, частью которых
служат его стороны; в противном случае он называется вогнутым.

В случае, когда многоугольник выпуклый каждый большой круг,
частью которого служит сторона многоугольника, делит сферу на две полусферы, из
которых одна содержит весь многоугольник; общая область R всех таких полусфер,
содержащих данный многоугольник, и будет внутренней областью многоугольника
(рис 9, 10).

Сферический
двуугольник-фигура,образованная двумя полуокружностями
больших кругов сферы, исходящими из диаметрально противоположных точек

В отличие от плоскости, где треугольник является
многоугольником с наименьшим числом сторон, на сфере имеются многоугольники с
числом сторон меньше трех- двуугольники. Двуугольником является часть сферы,
ограниченная двумя половинами больших окружностей с общими концами; эти общие
концы, называемые вершинами двуугольника, являются диаметрально
противоположными точками сферы.

 Сферический треугольник

Сферическим треугольником называется фигура,
состоящая из трех точек сферы и трех отрезков, попарно соединяющей эти точки.
Здесь под отрезками понимаем меньшую из двух дуг большой окружности, проходящей
через эти точки.

            Пусть ABC – сферический треугольник, — радиус векторы
вершин.(рис.12) Обозначим дуги , соответственно через  с, b, а.

Углом между дугами понимают угол между их
касательными векторами. Обозначим — угол между дугами и , — угол между и , — между

Три больших
окружности, пересекаясь попарно в двух точках, образуют на сфере восемь
сферических треугольников. Зная элементы (стороны и углы) одного из них

можно
определить элементы всех остальных, поэтому рассматривают соотношение между
элементами одного из них, того, у которого все стороны меньше половины большой
окружности.(рис.13)

Многие свойства сферического треугольника (а оно
одновременно являются и свойствами трехгранных углов) почти полностью повторяют
свойства обычного треугольника, среди них- неравенство треугольника или,
например, три признака равенства треугольника. Все планиметрические следствия
упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере.

Сумма углов всякого сферического треугольника всегда больше
180 . Разность (измеряется в радианах) – величина положительная и называется сферическим
избытком данного сферического треугольника.

Равнобедренные сферические треугольники

          
Сферический треугольник называется равнобедренным, если две его стороны
равны.

Всякий сферический треугольник, наложимый на треугольник, ему
симметричный, — равнобедренный.

Действительно, в силу того, что оба треугольника имеют противоположное
расположение, невозможно наложить один треугольник на другой так, чтобы
совпадали соответственные вершины, т.е. вершины, находящиеся первоначально на
концах одного диаметра; если бы среди сторон треугольника не было равных между
собой, то такое наложение было бы невозможно и ни каким другим образом.

Обратно, всякий равнобедренный сферический треугольник
наложим на треугольник, ему симметричный.

Если треугольник А’В’С’ симметричен треугольнику АВС и если
АВ равно АС, то два треугольника АВС и А’С’В’, имеющие (при выбранном порядке
вершин каждого из них) одно и тоже расположение, равны по второму признаку
равенства.

Теорема. В равнобедренном
сферическом треугольнике углы, противолежащие равным сторонам, равны.

Действительно, при совмещении треугольника АВС (АВ=АС) с
симметричным ему треугольником А’С’В’ угол, совпадающий с углом В’, есть угол
С’; таким образом, оба эти угла равны, и тоже самое имеет место и для углов С и
В’.

Обратно, всякий сферический треугольник, два угла
которого равны, равнобедренный.

Действительно, если АВС сферический треугольник, в которомÐВ=ÐС и треугольник А’В’С’
– треугольник, ему симметричный, то треугольники АВС и А’С’В’, имеющие
одинаковое расположение равны по первому признаку равенства, и, следовательно,
АВ=А’С’=АС.

Площадь сферического треугольника

Будем называть площадью сферической
фигуры, по аналогии с площадью плоской фигуры, действительное число,
удовлетворяющее следующим четырём требованиям:

1)      
площадь сферической фигуры является
положительным числом, (свойство позитивности),

2)      
площадь сферической фигуры не изменяется при
движении (свойство инвариантности),

3)      
если сферическая фигура разложена на две
сферические фигуры, то площадь данной фигуры равна сумме площадей двух фигур,
на которые она разложена (свойство аддитивности),

4)      
Площадь всей сферы радиуса R равна 4pR² (свойство нормировки).

.Сферическая теорема синусов

Теорема.
Синусы сторон сферического треугольника относятся как синусы противолежащих
углов.

Пусть
длины сторон сферического треугольника (рис. 14) равны а, b, с, а
противолежащие им углы этого треугольника равны А, В, С соответственно, r-
радиус сферы, тогда

                
рис.15                                 рис.16

Доказательство:
В сферическом треугольнике ABC проведем  вы­соту
СН — дугу большой окружности, перпендикулярную боль­шой окружности АВ (рис.
15). Длине высоты |СН|_sотвечает величина угла СОH: если , то |CH|_s=Rφ. Это
наводит на следующее построение для соответствующего трехгранного угла ОАВС. Возьмем
на ребре ОС произвольную точку C₁ и
проведем из нее перпендикуляры С₁А₁ к (ОA), С₁В₁к
(ОB)
и С₁Н₁к плоскости ОАВ (рис. 16); мы опять рассматриваем
случай острых углов α, β, . По
теореме о трех перпендику­лярах (H₁A₁)(OA), (H₁B₁)(OB), поэтому
углы C₁A₁H₁и C₁B₁H₁будут линейными углами соответствующих двугранных
углов:. Из
прямоугольных треугольников OA₁C₁и С₁Н₁А₁,
обозначив |OC₁|=z, находим:

 (1.1)

Аналогично
из прямоугольных треугольников ОВ₁С₁и C₁H₁B₁

 (1.2)

Приравнивая
правые части равенств (1.1) и (1.2), получим:

откуда

Точно так же
доказывается, что

Получающиеся в итоге
формулы

и
составляют содержание теоремы  синусов для  сферических треугольников или
трехгранных углов.

Сферическая теорема косинусов:

              (1.4)

Доказательство
проведём с помощью проекций. На рисунке показан сферический треугольник ABC
на сфере радиуса R с центром в точке O. BP — перпендикуляр
к плоскости большого круга, проходящего через сторону b, BM —
перпендикуляр к OC, BN — перпендикуляр к OA. По
утверждению, обратному теореме о трёх перпендикулярах, PM
— перпендикуляр к OC, PN — перпендикуляр к OA. Заметим,
что угол PMB равен π — C,кроме того,ON = Rcosc и OM = R
cos a. Далее, проецируем ломаную OMPN на прямую, содержащую ON.

,

,

,

.

Подставляем три
последних выражения и указанное выше выражение ON = R cos c в первое выражение
и получаем:          

.

Теоремы косинусов для
двух других сторон, то есть теорему для cos a и теорему для cos b, получаем
аналогично, их также можно получить сразу из формулы для стороны c при помощи
круговой перестановки букв:

  Теоремы косинусов для сферического треугольника со сторонами a, b, c и
углами A, B, C имеют следующий вид:

Эти две теоремы двойственны
по отношению друг к другу, поскольку углы и стороны всякого сферического
треугольника дополняются до развёрнутого угла сторонами и углами
соответствующего полярного
треугольника.

Следствие.

  Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора:

Сформулируем и докажем двойственную
теорему косинусов:

(1.7)

Запишем
для полярного треугольника A’B’C’ теорему косинусов

С
учетом формул (1.6), получим (1.7).

 Заметим, что внешне формулы косинусов на плоскости
и на сфере не­похожи. С другой стороны, на маленьких участках сферу мож­но
считать «почти плоской», тогда (т. е. при малых по сравне­нию с радиусом R сферы длинах сторон сферического треуголь­ника ABC) сферическая теорема косинусов должна «почти
перейти» в планиметрическую, и то же самое для теоремы сину­сов. Проверим, так
ли это.

Длины сторон а, b, сферического треугольника ABC свя­заны с соответствующими плоскими углами α, β, γ
трехгранного  угла ОАВС формулами

,

поэтому
рассматриваемый случай (а, b, с много
меньше, чем R) отвечает тому,
что α0, β0, γ0. Вспомним, что при малых φ зна­чение sinφ приближенно
равно φ:

Отсюда можно вывести
аналогичную приближенную формулу для соsφ при малых φ:

Подставляя
соответствующие приближения в формулы сину­сов и косинусов (формулы (6) и (3)),
получим приближенные формулы для малых сферических треугольников:

откуда

(отбросила в
предпоследнем соотношении слагаемое четвер­той степени , поскольку оно мало по сравнению со слагаемыми
второй степени —  ). Подставляя в полученные формулы  , действительно получаются обычные теоремы синусов
и косинусов.

Решение сферических
треугольников

Выведенные
тригонометрические соотношения позволяют «решить сферический треугольник» по любым трем из его элементов (сторон и
углов).

1. Даны три
стороны сферического треугольника. Найти углы треугольника.

Решение: по формуле, выражающей теорему косинусов, находим

и аналогично находим соsВ и  соs С.

2. Даны две стороны сферического треугольника и угол между ними, например стороны b,
с и угол А. Найти остальные элементы треугольника. Решение:  сторону
а найдем из
теоремы косинусов. Зная все три стороны сфери­ческого треугольника, найдем его
остальные углы, как указано выше.

3. Даны две стороны сферического треугольника и угол, лежащий против одной из них,
например стороны а, b и угол A. . Найти остальные элементы треугольника.

Решение: по теореме синусов находим

         .

Заметим, что эта формула даёт для В два значения,
дополняю­щих друг
друга доp; это
соответствует тому, что в общем случае два сферических треугольника с двумя соответственно
равными сто­ронами
и равными углами, лежащими против одной из этих сторон, не обязательно равны, а возможен
случай, когда углы этих треуголь­ников, лежащих против другой стороны, дополняют друг друга
до p.

Для
определения стороны с и угла С проведём через вершину С дугу большой окружности
АВ. Если эти большие окружности
пересекаются в точке D, то рассмотрим прямоугольные сферические треугольники АСD
и ВСD (рис.
19). В этих треугольниках известны гипотенузы b и а и углы при вершинах Аи В. Второй
катет каждого из этих треугольников определяется по первым формулам тангенсов, а угол при вершине С определится
по формуле котангенсов. 

Рис.19

Сторона
с и угол C
сферического
треугольника АВС являются суммами найденных сторон или углов прямоугольных треугольников, если точка D лежит на
стороне АВ, и разностям и этих сторон или углов, если точка D лежит на продолжении стороны АВ.
Именно, если
оба угла A,В в исходном треугольнике АВС являются острыми или оба тупыми, то
перпендикулярная к АВ окружность, проходящая через точку C,   пе­ресекает  окружность   АВ в
двух точках, одна из которых  лежит на дуге АВ; эту точку и следует принять за D в рассматриваемом
случае. Таким образом, углы при вершинах Аи В в прямоугольных треугольниках АСD
и ВСD сов­падают с углами А и В исходного треугольника
АВС, а сторона с и угол С треугольника АВС являются суммами
найденных нами сторон
или углов прямоугольных треугольников АСD и ВСD. Если же в треугольнике АВС один
из углов A, В острый, а второй—ту­пой, то перпендикулярная к АВ окружность,
проходящая через точку С, пересекает окружность АВ в двух точках, ни одна из которых не ле­жит на дуге АВ. В этом случае за D можно при­нять

Любую из этих то­чек, например ту, кото­рая лежит на продолжении стороны АВ за точку В(рис. 20).

Рис. 20

Таким образом, угол при вершине А в ∆АСD равен углу А треугольника АВС,
а угол при вершине В в ∆ВСD
равен p — В. При этом сторона с и угол С треугольника АВС являются
разностями сторон АD, ВD или углов
при вершине С треугольников АСD и ВСD. Наконец, если один из углов A, В (например, А) прямой,
то треугольник АВС прямоугольный,
и для нахождения стороны с и угла С можно в атом случае воспользоваться формулами  ,.

4. Даны три угла сферического треугольника. . Найти остальные элементы треугольника.

Решение: по фор­муле  двойственной теоремы косинусов
находим

и аналогично находим  и
.

5. Даны два угла сферического треугольника и сторона между ними, например сторона а
и углы B и C.
. Найти
остальные элементы треугольника.

Решение: угол А найдем по формуле  двойственной теоремы
косинусов. Зная все три угла сферического треугольника, найдем его остальные стороны, как указано выше.

6. Даны два угла сферического треугольника и сторона, лежащая против
одного из них, например углы А и В и сторона а. . Найти остальные
элементы треугольника.

Решение: по теореме синусов находим

                   .

Заметим, что эта формула дает для b два значения, дополняющих друг друга до pr; это соответствует тому, что
в общем слу­чае
два сферических треугольника с двумя соответственно равными углами и равными сторонами,
лежащими против одного из этих углов, не обязательно равны, а возможен случай, когда стороны
этих тре­угольников,
лежащие против другого угла, дополняют друг друга до pr. Сторону с и угол С по углам А,
В и сто­ронам а,
b найдем, как указано выше.

Примеры решения задач

Определение метра и морской мили

·        
R=6367 км – радиус Земного шара.

·        
Длина большой окружности Земли

·        
L=2πR

·        
L=2·3,1416·6367=40000 км.

·        
Один метр – одна 40- миллионная часть длины
земного экватора.

·        
Морская миля равна одной угловой минуте на
земном меридиане.

·        
В 60·360=21600 раз короче длины большой
окружности земного шара.

·        
1 морская миля равна  40000000м:21600=1852м

·        
Длина
земного экватора равна ровно 21600 морских миль

Задача1.Мореплаватель Христофор Колумб проплыл 1800
миль в одном направлении из точки А к точке В, повернул на 60 градусов и
проплыл в новом направлении еще 2700
миль, оказался в точке С. Требуется найти расстояние между точками А и С (по
поверхности земного шара).

Решение:Обозначим
через a, b и с длины дуг ВС, АС и АВ соответственно, y — внутренний угол при вершине
В сферического треугольника АВС. Тогда,

где
R= — радиус земного шара, выраженный в морских милях.По теореме косинусов
для сферического треугольника

По
таблицам или с помощью калькулятора находим, что

радиан.

Следовательно,
длина дуги АС= b равна b = R*0.90662 = 3437.4*0.906623116.7 миль.

Ответ:
3117 морских миль 5772 км.

Задача 2. Вывести формулу длины ортодромии — кратчайшего расстояния между точками на земной
поверхности с известными координатами (в предположении сферичности Земли).

Решение:Обозначим географические широты двух данных точек  и , разность долгот — , кратчайшее расстояние между ними обозначим d, длину дуги в 1
градус — a.(см.рис.) Тогда формула длины ортодромии:

Эта формула сразу получается применением теоремы косинусов
к стороне AB сферического треугольника P_nAB. Подобная формула справедлива для любой
сферической поверхности и поэтому её можно применять также для определения
углового расстояния между звёздами по известным их экваториальным координатам

Задача 3. Определить угловое расстояние между двумя светилами на небесной сфере
.

Решение: Определим
угловое расстояние (x) между звездой δ
Цефея (экваториальные координаты: α₁=22ч
29м, δ₁=+58° 25′) и галактикой Туманность Андромеды (α₂=0ч 43м, δ₂=+41°
16′) на небесной сфере. Выражаем α₁ в градусах и долях градуса:

Аналогично получаем,
что α₂=10°,75. Выражаем δ₁ в градусах и долях градуса:

Аналогично δ₂=41°,27.
Применяем теорему косинусов:

Отсюда x=27°,11.

Заключение

В
данной курсовой работе я познакомилась со сферической геометрией, которая
изучает геометрические образы, находящиеся на сфере, подобно тому, как
планиметрия изучает геометрические образы, находящиеся на плоскости. Я 
рассмотрела основные понятия, установила соответствие между сферической
геометрией и планиметрией. А также рассмотрела практические задачи, необходимые
мореплавателям, летчикам и космонавтам. В настоящее время сферическая геометрия
особенно широ­кое применение находит в астрономии и геодезии (науке о фор­ме и
размерах Земли), навигации и картографии.

       Одной из важнейших
астрономических задач, без которой невозможно решение всех остальных задач
астрономии, является определение положения небесного светила на небесной сфере.

       Многие важные открытия, как в
прошлом, так и сегодня были бы невозможными без упорного, тяжелого и часто
незаметного труда ученых, посвятивших свою жизнь определению небесных координат
светил.

      Без результатов
20-летнего труда Тихо Браге, этого искусного измерителя координат планет,
Иоганн Кеплер не смог бы открыть законы движения планет вокруг Солнца. Точные
определения положения светил на небесной сфере позволили установить, в
частности, место малых планет и комет в Солнечной системе, открыть Нептун и
Плутон. Методы определения координат небесных светил (их видимых положений на
небе) разрабатывались на протяжении свыше двух тысячелетий. Сегодня они
составляют один из важнейших разделов астрономии, который называется
астрометрией.

Список литературы

1. Избранные вопросы математики: 10 Кл. Факультативный курс/А.М.
   Абрамов, Н.Я. Виленкин, Г.В. Дорофеев и др.; Сост.: С.И. Шварцбурд.- М.:
   Просвещение, 1980. — 191 с.
2. Атаносян Л.С. Геометрия. Часть 2. – М.: Просвещение, 1974.
3. Энциклопедия элементарной математики, книга IV, V. Геометрия. – М.: Наука, 1966. – 624 с.
4. Адамар
   Ж. Элементарная геометрия. Ч.2. М. Учпедгиз, 1958. Андреев
5. Базылев
   В.Т. Геометрия. М: Просвещение, 1975.
6. Базылев
   В.Т. Сборник задач по геометрии. М: Просвещение, 1980. -240с.
7. Егоров
   И.П. Основания геометрии. – М: Просвещение, 1984. – 144с.
8. Розенфельд
   Б.А. История неевклидовой геометрии. Развитие понятия о геометрическом
   пространстве. М. Наука., 1976. – 408с.
9. Энциклопедия
   элементарной математики. Кн.4 – Геометрия. М., 1963.
10. www.allbest.ru/referat
11. http://ru.wikipedia.org