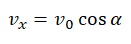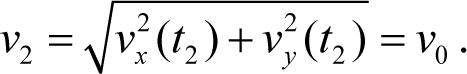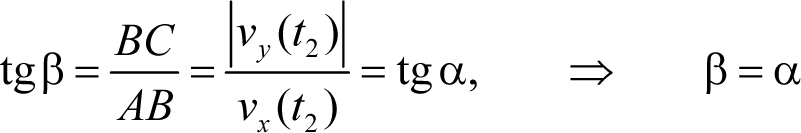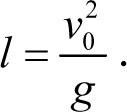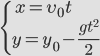Движение тела, брошенного под углом к горизонту
теория по физике 🧲 кинематика
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты! График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
Уравнение координаты x:
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Алгоритм решения
Решение
Запишем исходные данные:
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Потенциальная энергия шарика в точке А равна:
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
Перед ударом кинетическая энергия шарика равна:
Согласно закону сохранения энергии:
E p A = E p B + E k B
m g H = m g l 1 + m v 2 2 . .
Отсюда высота H равна:
H = m g l 1 m g . . + m v 2 2 m g . . = l 1 + v 2 2 g . .
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h − l 1 = v 2 sin 2 . β 2 g . . = v 2 sin 2 . ( 90 − 2 α ) o 2 g . .
l 1 = h − v 2 sin 2 . ( 90 − 2 α ) o 2 g . .
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
H = l 1 + v 2 2 g . . = h − ( g t ) 2 sin 2 . ( 90 − 2 α ) o 2 g . . + ( g t ) 2 2 g . .
H = h − g t 2 sin 2 . ( 90 − 2 α ) 2 . . + g t 2 2 . . = h − g t 2 2 . . ( sin 2 . ( 90 − 2 α ) o − 1 )
H = 1 , 4 − 10 · 0 , 4 2 2 . . ( sin 2 . ( 90 − 6 0 ) o − 1 )
H = 1 , 4 − 5 · 0 , 16 ( sin 2 . 3 0 o − 1 )
H = 1 , 4 − 0 , 8 ( ( 1 2 . . ) 2 − 1 ) = 1 , 4 − 0 , 8 ( 1 4 . . − 1 )
H = 1 , 4 + 0 , 6 = 2 ( м )
pазбирался: Алиса Никитина | обсудить разбор | оценить
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Найти угол между вектором скорости и горизонтом
Математический маятник представляет собой тяжёлый шарик, подвешенный на нерастяжимой нити длиной 1 м. Этот маятник совершает малые свободные колебания так, что нить всё время находится в одной вертикальной плоскости и отклоняется от вертикали на максимальный угол 3°. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение маятника.
1) Ускорение шарика всегда направлено вдоль его нити.
2) Ускорение шарика постоянно по модулю.
3) Период колебаний маятника равен примерно 2 с.
4) Угол между вектором скорости шарика и горизонтом не может быть больше 3°.
5) Модуль скорости шарика может быть больше 25 см/с.
1. Неверно. При колебаниях возвращающая сила направлена к положению равновесия. Следовательно, ускорение также направлено к положению равновесия и только в этой точке оно направлено вдоль нити.
2. Неверно. При колебаниях вектор ускорения меняется и по модулю, и по направлению.
3. Верно. Период колебаний математического маятника рассчитывается по формуле
4. Верно. Вектор скорости направлен по касательной к траектории, в крайних точках скорость равна 0. Из соображений геометрии угол между горизонтом и вектором скорости не может быть больше 3°.
5. Неверно. Максимальная скорость определяется формулой
ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
Из второй формулы (5.7) и третьего из уравнений (5.2) найдем величину конечной скорости тела v 2 :
Угол подлета тела к земле – это угол между вектором скорости тела и поверхностью земли. Этот угол можно найти из треугольника, гипотенузой которого является вектор скорости, катетами – его проекции на горизонтальную и вертикальную оси (треугольник АВС , см. рис. 5.2). Имеем
(модуль от проекции vy ( t 2) мы взяли потому, что эта проекция отрицательна).
Из полученных соотношений следует, что: (а) полное время движения вдвое больше времени подъема на максимальную высоту (и, следовательно, время подъема равно времени спуска), (б) конечная скорость равна начальной, (в) угол падения равен углу бросания. При этом эти результаты получались «сами» из уравнений движения, то есть их не пришлось предполагать заранее.
Отметим также, что при фиксированной величине начальной скорости дальность полета тела максимальна, если sin 2α = 1 (см. первое из соотношений (5.7)), или α = 45° . При этом сама максимальная дальность полета тела равна
Важной особенностью описания равноускоренного криволинейного движения является возможность представить его как совокупность двух движений: равномерного в направлении, перпендикулярном ускорению, и равноускоренного в направлении ускорения (эту особенность первым понял Г. Галилей). Действительно, уравнения движения, которые получаются в результате проецирования уравнений (5.1) на перпендикулярную и параллельную ускорению оси оказываются такими же, как для равномерно и равноускоренно движущегося тела. Такая возможность позволяет значительно упростить анализ уравнений движения. В качестве примера рассмотрим следующую задачу.
http://phys-ege.sdamgia.ru/problem?id=23292
http://online.mephi.ru/courses/physics_origins/data/72.html
- Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
- Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
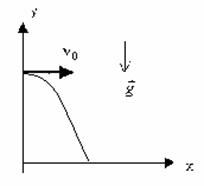
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
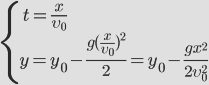
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Решим задачу для случая х0=0 и y0=0.
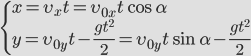
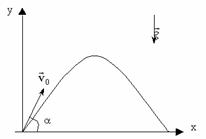
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
.
Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
Время полета:


Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: 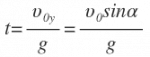
Время подъема:
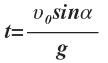
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
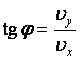
Движение тела под углом к горизонту, теория и онлайн калькуляторы
Движение тела под углом к горизонту
Начальные условия
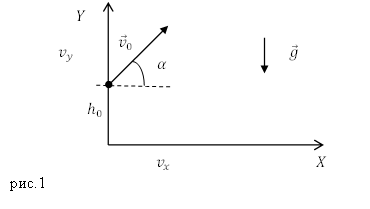
Рассмотрим движение тела (материальной точки) брошенного под углом к горизонту с некоторой высоты $h_0$. Начальная
скорость тела равна ${overline{v}}_0$, вектор ${overline{v}}_0$ составляет угол $alpha $ с горизонтом (рис.1). Систему отсчета, в которой движется тело, свяжем с Землей. Ось X направим параллельно земле, ось Y вертикально вверх.
Движение тела под углом к горизонту происходит в поле тяжести Земли под воздействием силы тяжести. Силой сопротивления воздуха пренебрежём. В этом случае ускорение тела ($overline{a}$) совпадает с ускорением свободного падения ($overline{g}$):
[overline{a}=overline{g}left(1right),]
где $g=9,8 frac{м}{с^2}$.
Запишем начальные условия движения тела (рис.1):
[ left{ begin{array}{c}
xleft(t=0 right)=0, \
yleft(t=0 right)=h, \
v_xleft(t=0 right){=v}_{0x}=v_0{cos alpha , } \
v_yleft(t=0 right){=v}_{0y}=v_0{sin alpha . } end{array}
right.left(2right).]
Уравнение для перемещения тела, брошенного под углом к горизонту. Траектория его движения
Перемещение тела, которое бросили под углом к горизонту является равноускоренным, следовательно, для написания уравнения движения воспользуемся векторным уравнением для перемещения ($overline{s}$) при равнопеременном движении в виде, учтем равенство (1):
[overline{s}(t)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(3right).]
Векторное уравнение (3) в проекции на оси координат X и Y даст нам два скалярных уравнения:
[left{ begin{array}{c}
x(t)=v_0{cos alpha }t \
y(t)=h_0+v_0{sin alpha }t-frac{gt^2}{2} end{array}
right.left(4right).]
Из системы уравнений (4) мы видим, что при рассматриваемом нами движении происходит наложение двух прямолинейных движений.
Причем по оси X тело под углом к горизонту движется с постоянной скоростью ${ v}_{0x}=v_0{cos alpha , }$ а по оси Y материальная точка перемещается с постоянным ускорением $overline{g}$. Уравнение траектории движения тела можно получить, если из первого уравнения системы (4) выразить время ($t$) полученный результат подставить во вторую формулу системы:
[t=frac{x}{v_0{cos alpha }};; ]
[y(x)=h_0 tg alpha -frac{g}{2}{left(frac{x}{v_0{cos б }}right)}^2left(5right).]
Уравнение $y(x)$ (функция (5)) показывает, что тело движется по параболе в плоскости, в которой лежат векторы $overline{g}$ и ${overline{v}}_0.$
Уравнение скорости движения тела брошенного под углом к горизонту
В векторном виде уравнение для скорости движения рассматриваемого нами тела в произвольный момент времени запишем:
[overline{v}(t)={overline{v}}_0+overline{g}tleft(6right).]
В скалярном виде уравнение (6) представим в виде системы уравнений:
[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(7right).]
В системе уравнений (7) мы еще раз видим, что движение тела под углом к горизонту по оси X равномерное, по оси Y равнопеременное. Причем, двигаясь вверх, тело уменьшает свою скорость от $v_{0y}$ до нуля, затем падая вниз скорость тела увеличивается.
Модуль вектора скорости в производный момент времени для рассматриваемого нами движения найдем как:
[v=sqrt{v^2_x{+v}^2_y left(8right).}]
Время подъема и полета тела
Время, которое тело тратит на полет вверх в рассматриваемом движении можно найти из второго уравнения системы (7). В точке максимального подъема вектор скорости точки параллелен оси X, значит $v_y=0$, тогда время подъема ($t_p$):
[t_p=frac{v_0{sin alpha }}{g}left(9right).]
Время, которое тело находилось в воздухе (время полета($t_{pol}$)) получим из второго уравнения системы (4), приравняв ординату $y$ к нулю:
[t_{pol}=frac{v_0{sin alpha +sqrt{v^2_0{sin}^2alpha +2gh_0} }}{g}left(10right).]
При $h_0=0$ мы видим, что $t_{pol}=2t_p.$
Дальность полета и высота подъема
Для того чтобы найти горизонтальную дальность полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (4) подставим время полета ($t_{pol}$) (10). При $h_0=0,$ дальность полета равна:
[s=frac{v^2_0{sin left(2alpha right) }}{g}left(11right).]
Максимальную высоту подъема тела под углом к горизонту ($h_{max}$) находят из второго уравнения системы (4), подставляя в него время подъема ($t_p$) (9):
[h_{max}=h_0+frac{{v_0}^2{{sin}^2 б }}{2g}left(12right).]
Примеры задач с решением
Пример 1
Задание. Каким будет угол ($alpha $) под которым бросили тело к горизонту, если оказалось, что максимальная высота подъема ($h$) тела в четыре раза меньше, чем дальность его полета ($s$)? Сопротивление воздуха можно не учитывать.
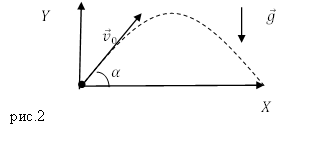
Решение. Выберем систему отсчета связанную с Землей. Будем считать, что тело бросили из начала координат (рис.2).
Запишем кинематические уравнения движения тела в поле тяжести земли:
[overline{s}(t)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(1.1right).]
[overline{v}(t)={overline{v}}_0+overline{g}tleft(1.2right)]
Исходя из начальных условий, нашей задачи:
[left{ begin{array}{c}
{overline{s}}_0=0 \
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha } end{array}
right. left(1.3right).]
В проекциях на оси уравнения (1.1) и (1.2)предстанут в виде:
[left{ begin{array}{c}
x(t)=v_0{cos alpha }t \
y(t)=v_0{sin alpha }t-frac{gt^2}{2} end{array}
right.left(1.4right).]
[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(1.5right).]
Время подъема из второго уравнения системы (1.5) равно:
[t_p=frac{v_0{sin alpha }}{g} left(1.6right).]
Тогда максимальная высота подъема равна:
[h=yleft(t_pright)=frac{v^2_0{sin}^2alpha }{2g}left(1.7right).]
Если тело бросили из начала координат, то $t_{pol}=2t_p,$ дальность полета найдем, подставив время полета в первое уравнение системы (1.4):
[s=xleft(t_{pol}right)=2v^2_0frac{{{cos alpha }sin alpha }}{g} left(1.8right).]
По условию задачи: $h=frac{s}{4}$, используем уравнения (1.7) и (1.8):
[frac{v^2_0{sin}^2alpha }{2g}=v^2_0frac{{{cos alpha }sin alpha }}{2g}to {sin alpha }={cos alpha }to alpha =frac{pi }{4}.]
Ответ. $alpha =frac{pi }{4}$
Пример 2
Задание. Какова скорость падения тела брошенного под углом горизонта $alpha $ со скоростью $v_0$? Если тело бросили с земли. Сопротивление воздуха можно не учитывать.
Решение. За основу решения задачи примем кинематическое уравнение для скорости движения тела в поле тяжести Земли:
[overline{v}left(tright)={overline{v}}_0+overline{g}tleft(2.1right).]
Начальные условия движения нашего тела:
[left{ begin{array}{c}
{overline{s}}_0=0 \
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha } end{array}
right. left(2.2right).]
В проекциях на оси X и Y уравнение (2.1):
[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(2.3right).]
Время подъёма тела, принимая во внимание, что $v_yleft(t_pright)=0$ из второго уравнения (2.3) равно:
[t_p=frac{v_0{sin alpha }}{g} left(2.4right).]
Если тело бросили из начала координат, то $t_{pol}=2t_p:$
[t_{pol}=frac{2v_0{sin alpha }}{g}left(2.5right).]
Зная время полета, найдем $v_yleft(t_{pol}right)$, подставив его во второе уравнение (2.3):
[v_yleft(t_{pol}right)=-v_0{sin alpha left(2.6right). }]
Модуль вектора скорости в момент падения найдем как:
[v(t_{pol})=sqrt{v^2_x{+v}^2_y }=v_0.]
Ответ. При заданных условиях величина скорости падения равна модулю скорости бросания.
Читать дальше: динамика прямолинейного движения связанных тел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Что такое движение тела брошенного под углом к горизонту
Определение
Движением тела под углом к горизонту в физике называют сложное криволинейное перемещение, которое состоит из двух независимых движений, включая равномерное прямолинейное движение в горизонтальном направлении и свободное падение по вертикали.
В процессе подбрасывания объекта вверх под углом к горизонту вначале наблюдают его равнозамедленный подъем, а затем равноускоренное падение. Скорость перемещения тела, относительно поверхности земли, остается постоянной.
На графике изображено схематичное движение тела, которое подбросили под углом к горизонту. В этом случае α является углом, под которым объект начал свое перемещение. Характеристики такого процесса будут следующими:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Направление вектора скорости тела, которое подбросили под определенным углом к горизонту, будет совпадать с касательной к траектории его перемещения.
- Начальная скорость отличается от направления горизонтальной линии, а обе ее проекции не равны нулю.
- Проекция скорости в начале движения на ось ОХ составляет (V_{ox}=V_{0}cos alpha).
- Проекция начальной скорости на ось ОУ равна (V_{oy}=V_{0}sin alpha).
- Проекция мгновенной скорости на ось ОХ следующая: (V_{x}=V_{0}cos alpha).
- Проекция мгновенной скорости на ось ОУ обладает нулевым значением и рассчитывается следующим образом: (V_{x}=V_{0}sin alpha-gt).
- Ускорение свободного падения на ось ОХ обладает нулевой проекцией, или (g_{x}=0).
- Проекция ускорения свободного падения на ось ОУ равна (–g), или (g_{y}=-g).
К числу кинематических характеристик движения тела, которое подбросили под углом к горизонту, относят модуль мгновенной скорости в определенное время t. Данный показатель можно рассчитать с помощью теоремы Пифагора:
(V=sqrt{V^{2}_{x}+V^{2}_{y}})
Минимальная скорость тела будет замечена в самой верхней точке траектории, а максимальная величина данной характеристики будет достигнута, когда объект только начинает перемещаться, а также в точке падения на поверхность земли. Время подъема представляет собой время, необходимое для достижения телом верхней точки траектории. За полное время объект совершает полет, то есть перемещается от начальной точки к точке приземления.
Дальность полета является перемещением объекта по отношению к оси ОХ. Такую кинематическую характеристику обозначают буквой l. По отношению к оси ОХ тело перемещается, сохраняя постоянство скорости.
Определение
Горизонтальным смещением тела называют смещение данного объекта, относительно оси ОХ.
Расчет горизонтального смещения тела в какой-либо момент времени t выполняют с помощью уравнения координаты х:
(x=x_{0}+V_{0x}t+frac{gxt^{2}}{2})
Зная следующие условия:
- (x_{0}=0);
- проекция ускорения свободного падения, относительно оси ОХ, также имеет нулевое значение;
- проекция начальной скорости на ось ОХ составляет (V_{0}cos alpha).
Записанная формула приобретает следующий вид:
(x=V_{0}cos alpha t)
Мгновенной высотой принято считать высоту, на которой находится объект в определенный момент времени t. Наибольшей высотой подъема является расстояние от поверхности земли до верхней точки траектории движения тела под углом к горизонту.
Вывод формулы, как найти угол и дальность полета
Перемещение объекта, который был брошен под углом к горизонту, необходимо изобразить с помощью суперпозиций, характерных для двух типов движений:
- равномерное горизонтальное движение;
- равноускоренное перемещение в вертикальном направлении с ускорением свободного падения.
Скорость тела будет рассчитываться таким образом:
(v_{0x}=v_{x}=v_{0} cos alpha =const)
(v_{0y}=v_{0}sin alpha)
(v_{y}=v_{0}sin alpha-gt)
Уравнение координаты записывают в следующем виде:
(x=v_{0}cos alpha times t)
(y=v_{0}sin alpha times t-frac{gt^{2}}{2})
В любое время значения скорости тела будут равны:
(v=sqrt{v_{x}^{2}+v_{y}^{2}})
Определить угол между вектором скорости и осью ОХ можно таким образом:
(tan beta =frac{v_{y}}{v_{x}}=frac{v_{0}sin alpha -gt}{v_{0}cos alpha })
Время подъема на максимальную высоту составляет:
(t=frac{v_{0}sin alpha }{g})
Максимальная высота подъема будет рассчитана следующим образом:
(h_{max}=frac{v_{0}^{2}sin ^{2}alpha}{2g})
Полет тела будет длиться определенное время, которое можно рассчитать с помощью формулы:
(t=frac{2v_{0}sin alpha }{g})
Максимальная дальность полета составит:
(L_{max}=frac{v_{0}^{2}sin 2alpha }{g})
Примеры решения задач
В примерах, описывающих движение тела, на которое действует сила тяжести, следует учитывать, что а=g=9,8 м/с2.
Задача 1
Небольшой камень был брошен с ровной горизонтальной поверхности под углом к горизонту. Необходимо определить, какова максимальная высота подъема камня при условии, что, спустя 1 секунду после его начала движения, скорость тела обладала горизонтальным направлением.
Решение
Направление скорости будет горизонтальным в верхней точке перемещения камня. Таким образом, время, за которое он поднимется, составляет 1 секунду. С помощью уравнения времени подъема можно представить формулу произведения скорости в начале полета на синус угла, под которым бросили камень:
(V_{0}sin alpha =gt)
Данное равенство следует подставить в уравнение для расчета максимальной высоты, на которую поднимется камень, и выполнить вычисления:
(h=frac{V_{0}sin ^{2}alpha }{2g}=frac{(gt)^{2}}{2g}=frac{gt^{2}}{2}=frac{10times 1}{2}=5)
Ответ: максимальная высота подъема камня, который бросили под углом к горизонту, составляет 5 метров.
Задача 2
Из орудия выпустили снаряд, начальная скорость которого составляет 490 м/с, под углом 30 градусов к горизонту. Нужно рассчитать, какова высота, дальность и время полета снаряда без учета его вращения и сопротивления воздуха.
Решение
Систему координат и движение тела можно представить схематично:
Составляющие скорости, относительно осей ОХ и ОУ, будут совпадать во время начала движения снаряда:
(V_{0x}=V_{0} cos alpha) сохраняет стабильность значения в любой промежуток времени во время всего перемещения тела.
(V_{0y}=V_{0}sin alpha) будет меняться, согласно формуле равнопеременного движения (V_{y}=V_{0}sin alpha-gt).
В максимальной точке, на которую поднимется снаряд:
(V_{y}=V_{0}sin alpha-gt_{1}=0)
Из этого равенства следует:
(t=frac{V_{0sin alpha }}{g})
Полное время полета тела будет рассчитано по формуле:
(t=2t_{1}=frac{2V_{0}sin alpha }{g}=50)
Высота, на которую поднимется снаряд, определяется с помощью уравнения равнозамедленного перемещения тела:
(h=V_{0y}t_{1}-frac{gt_{1}^{2}}{2}=frac{V_{0}^{2}sin ^{2}alpha }{2g}=3060)
Дальность полета снаряда будет рассчитана таким образом:
(S=V_{0x}t=frac{V_{0}^{2}sin 2alpha }{g}=21000)
Ответ: высота составляет 3060 метров, дальность полета равна 21000 метров, время движения составит 50 секунд.
Рассмотрим тело, брошенное под углом к горизонту. Пусть сопротивление воздуха будет очень малой величиной, такой малой, что мы сможем ей пренебречь.
Благодаря силе притяжения земли тело часть пути будет подниматься над поверхностью, а часть – опускаться к поверхности. Траектория полета такого тела – это парабола (рис. 1).
Рис. 1. Парабола – это траектория тела, брошенного под углом к горизонту
Разложим скорость тела
Вместо того, чтобы рассматривать сложное движение одного тела по параболе, будем рассматривать одновременное и более простое движение двух тел. Одно тело движется по вертикали, а второе – по горизонтали. Тела одновременно стартуют и заканчивают движение.
Мы сможем сложное движение разделить на два простых, как только разложим на проекции скорость тела. Полученные скорости будем рассматривать, как скорости отдельно двигающихся тел.
Любой вектор, направленный под углом к осям, можно разложить на проекции — вертикальную и горизонтальную (рис. 2).
Рис. 2. Вектор начальной скорости тела раскладываем на проекции, после этого можно каждую проекцию рассматривать отдельно
Формулы разложения скорости выглядят так:
[ large boxed{ begin{cases} v_{0y} = v cdot sin(alpha) \ v_{0x} = v cdot cos(alpha) end{cases} } ]
Вертикальная и горизонтальная проекции скорости
Обратим внимание теперь на рисунок 3.
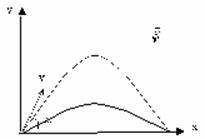
Рис. 3. Вертикальная часть скорости сначала уменьшается, а потом растет, а горизонтальная часть – не меняется
На рисунке черным цветом обозначен вектор скорости летящего тела. Видно, что от точки к точке он изменяется не только по модулю, но и по направлению. То есть, меняются характеристики вектора.
Вектор, обозначенный синим цветом на рисунке – это горизонтальная проекция вектора скорости. Заметно, что горизонтальная часть скорости не меняется ни по длине, ни по направлению, то есть, остается постоянной (одной и той же).
Вертикальная проекция скорости обозначена на рисунке красным цветом. При движении вверх она уменьшается, а при движении вниз – растет.
В самой высокой точке траектории вертикальная проекция скорости превращается в ноль. Из-за этого в верхней точке скорость направлена только горизонтально и равна числу ( v_{0x}). Число ( v_{0x}) – это горизонтальная проекция начальной скорости ( v_{0}) тела.
Упростить сложное движение тела на плоскости можно, рассматривая отдельно движение двух тел: одно тело движется по вертикали, меняя свою скорость, а второе – по горизонтали и, скорость свою не меняет.
Из рисунка 3 так же, следует, что
если тело при падении вернется на уровень, с которого оно стартовало, то:
- скорость, с которой мы подбросим тело, по модулю будет равна скорости, с которой тело упадет;
- угол (alpha) между скоростью тела на старте и осью Ox будет равен углу между конечной скоростью и горизонталью;
- время подъема равняется времени спуска;
Запишем теперь формулы, описывающие движение тела, под углом к горизонту. Разделим движение тела на две части: подъем и спуск. Вертикальное движение тела происходит под действием силы тяжести.
Подъем
Когда тело поднимается, оно проходит вертикальный путь (h):
[ large h = v_{0y} cdot t_{text{вверх}} — g cdot frac{t_{text{вверх}}^2}{2} ]
Вертикальная часть скорости уменьшается – движение равнозамедленное:
[ large v_{y} = v_{0y} — g cdot t_{text{вверх}} ]
Горизонтальная часть скорости остается такой же, как была в начале пути.
[ large v_{x} = v_{0x} ]
Поэтому вдоль горизонтали движение равномерное, т. е. происходит с неизменной скоростью
[ large S_{1} = v_{0x} cdot t_{text{вверх}}]
Эти формулы можно записать в виде системы:
[ large boxed{ begin{cases} v_{y} = v_{0y} — g cdot t_{text{вверх}} \ h = v_{0y} cdot t_{text{вверх}} — g cdot frac{t_{text{вверх}}^2}{2} \ S_{1} = v_{0x} cdot t_{text{вверх}} end{cases} } ]
На максимальной высоте траектории скорость имеет только горизонтальную проекцию (вертикальной скорости нет, скорость только горизонтальная).
[ large boxed{ begin{cases} h = h_{max} \ v_{y} = 0 \ v = v_{0x} end{cases} } ]
Спуск
При спуске, вертикальная проекция скорости растет – движение равноускоренное
[ large v_{y} = 0 + g cdot t_{text{вниз}} ] ,
Тело спускается, вертикальное перемещение можно найти из соотношения
[ large h = g cdot frac{t_{text{вниз}}^2}{2} ]
Горизонтальная часть скорости – все так же, меняться не будет. Поэтому движение вдоль горизонтали происходит с неизменной скоростью и тело проходит вторую часть горизонтального пути
[ large S_{2} = v_{0x} cdot t_{text{вниз}} ]
Объединим эти формулы в систему
[ large boxed{ begin{cases} v_{y} = 0 + g cdot t_{text{вниз}} \ h = g cdot frac{t_{text{вниз}}^2}{2} \ S_{2} = v_{0x} cdot t_{text{вниз}} end{cases} } ]
После того, как мы найдем время подъема и время спуска, можем найти общий путь по горизонтали:
[ large boxed{ S = S_{1} + S_{2} = v_{0x} cdot left(t_{text{вверх}} + t_{text{вниз}} right)}]