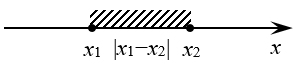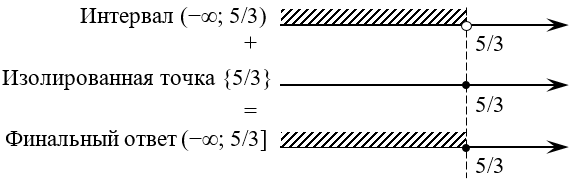Модуль числа, определение и свойства
Определение модуля числа
Алгебра дает четкое определения модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой «A» — расстояние от точки «A» до начала отсчёта (то есть до нуля, длина отрезка «OA») будет называться модулем числа «a».
Знак модуля: |a| = OA
Разберем на примере:
Точка «В», которая соответствует числу «−3», находится на расстоянии 3 единичных отрезков от точки 0 (то есть от начала отсчёта). То есть длина отрезка «OB» равна 3 единицам.
Число 3 (длина отрезка «OB») называют модулем числа «−3».
Обозначение модуля: |−3| = 3
Читают символы выше следующим образом: «модуль числа минус три равен трем».
Точка «С», которая соответствует числу «+4», находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка «OС» равна четырем единицам.
Число 4 называют модулем числа «+4» и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
- |−a| = a, если a < 0
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
- |a b| = |a| |b|, когда
a·b 0
или
−(a·b), когда a·b<0
7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя:
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
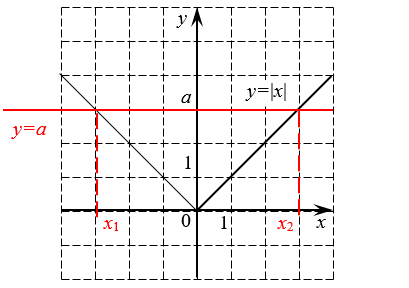
Решим уравнение: |х| = 5
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой. Или длине отрезка АВ
Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.
Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.
Решим неравенство: |a + 7| < 4 .
Эту запись читаем так: расстояние от точки a до точки −7 меньше четырёх. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:
Ответ в данном случае будет таким: (-11; -3).
Решим неравенство: |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
Ответ: ( -; 3] [17, +)
График функции
График функции равен y = |х|.
Для x 0 имеем y = x.
Для x < 0 имеем y = −x. В результате получаем:
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
В контрольной или задаче ЕГЭ может встретиться задачка, в которой просят вычислить √a2 , где a – некоторое число или выражение.
При этом, √a2= |a|.
По определению арифметического квадратного корня √a2 — это такое неотрицательное число, квадрат которого равен a2 .
Оно равно a, при а 0 и -а, при а < 0 , т. е. как раз |a|.
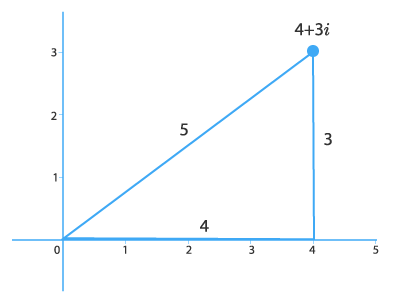
Модуль комплексного числа
У нас есть комплексное число, которое выглядит следующим образом: z=x+i·y, где x и y представляют собой действительную и мнимую части комплексного числа z (и являются действительными), а i — мнимая единица и равна √-1
Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:
Свойства модуля комплексных чисел
- Область определения: вся комплексная плоскость.
- Область значений: [0;+∞).
- Модуль как комплексная функция не дифференцируется ни в одной точке, так как условия Коши-Римана не выполнены.
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Модуль рационального числа, примеры:
|-3,5| = 3,5
|0| = 0
Модуль вещественных чисел
- Область определения: (−∞;+∞).
- Область значений: [0;+∞).
- Функция чётная.
- Функция дифференцируется везде, кроме нуля. В точке x=0 функция претерпевает излом.
Модуль противоположного числа, нуля, отрицательного и положительного чисел
Исходя из свойств модуля, которые мы рассмотрели выше, получаем:
- Противоположные числа имеют равные модули, то есть |- а| = |а| = a.
Если посмотреть это относительно координатной прямой, то две точки, у которых координаты — это противоположные числа, располагаются на одном расстоянии от начала отсчета. То есть модули противоположных чисел одинаковы. - Модуль нуля равен нулю.
|0| = 0, если a = 0 - Для положительного числа модуль равен самомý числу, а для отрицательного – противоположному числу.
|а| = — а
|−a| = a
что это такое и как его найти?
Модуль — математическое понятие, которое проходят в шестом классе.
Модуль с точки зрения геометрии
Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.
Как найти модуль числа?
Теперь, когда мы визуально представляем, что же такое модуль, будет проще понять формулировку из учебника.
Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.
Это можно сформулировать и иначе — модулем любого числа будет само это число в абсолютном выражении, то есть без учета знака. Записывается модуль так — по обе стороны от нужного числа ставятся вертикальные линии, например, модуль для числа «5» будет равен «5», а записываться он будет, как |5|.
Из всего, что мы рассказали выше, можно вывести несколько строгих правил для модулей.
- Может ли модуль быть отрицательным? Нет! Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, -7, то его модуль будет равен |7| — числу, противоположному исходному.
- Для нуля модуль всегда будет равен нулю. Верно и другое — нуль может быть модулем исключительно в том случае, если вычисляется он для числа нуль, и ни в каком другом.
- Если нужно найти модуль для выражения типа a*b, то есть модуль произведения, то можно сначала найти модуль а, затем модуль b, и перемножить их друг на друга.
- То же самое касается и деления — если нам нужно разделить y на z и найти модуль получившегося числа, то можно взять модуль y и разделить его на модуль z. Результат будет одним и тем же.
Похожие статьи
Как посчитать модуль числа в Эксель: формула, функция
Модуль (или абсолютная величина) – это неотрицательное значение любого числа. То есть, например, для отрицательного числа -32 он равняется 32, в то время, как для любого положительного числа равен этому же числу.
Давайте посмотрим, как найти модуль числа в Эксель.
Использование функции ABS
В программе Excel для нахождения модуля числа предусмотрена специальная функция
ABS, формула которой в общем виде может выглядеть так:
- ABS(число)
- ABS(адрес_ячейки_с_числом)
Допустим, нам нужно найти модуль числа -27.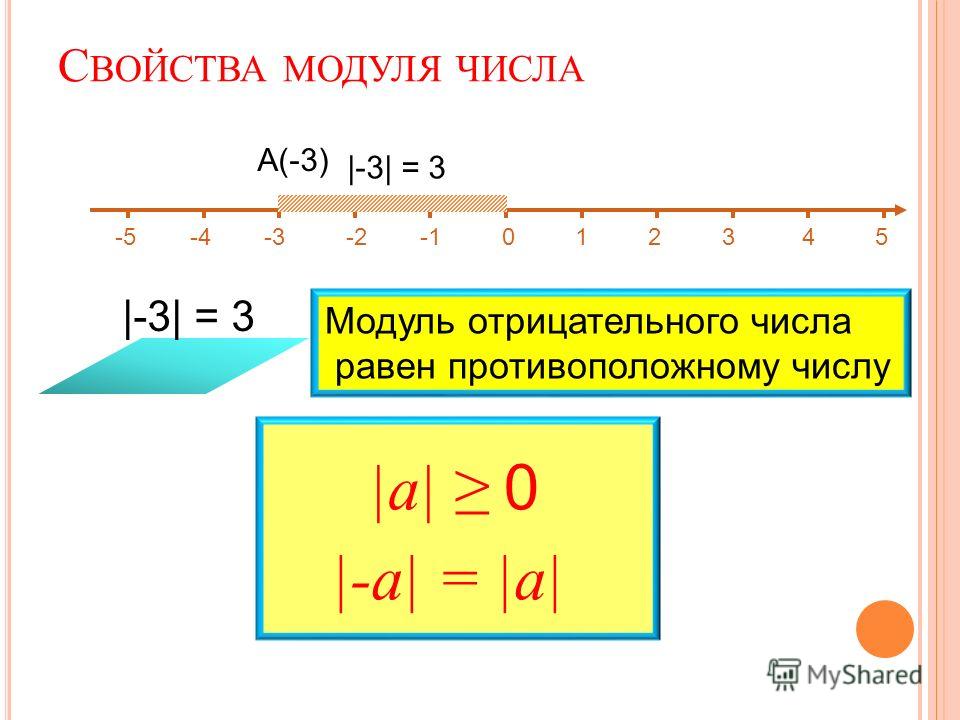
=ABS(-27).
Нажав клавишу Enter получаем результат в выбранной ячейке.
Некоторые пользователи по привычке пишут в ячейке математическое выражение, а именно, |-27|.
В данном случае после нажатия Enter программа выдаст ошибку.
Вместо того, чтобы вручную прописывать формулы, можно использовать Мастер функций.
- Выбрав ячейку, куда мы планируем добавить функцию и провести расчеты, кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
- В открывшемся окне вставки функций выбираем категорию
“Математические”, в предложенном списке кликаем по оператору “ABS” и жмем OK. - На экране отобразится окно для заполнения аргумента функции – “Число”. Адрес ячейки с числовыми значением, модуль которого нужно посчитать, можно указать вручную, либо просто кликнуть по ней в самой таблице.
Курсор при этом должен находиться в поле для ввода значения аргумента. По готовности жмем кнопку OK.
- В ячейке с функцией появится результат вычислений.
- Если нужно посчитать модули по всему столбцу, можно растянуть формулу на другие строки. Для этого наводим указатель мыши на ячейку с результатом, когда появится небольшой черный плюсик, зажав левую кнопку мыши тянем его вниз до последней ячейки столбца (или до той ячейки, для которой нужно посчитать аналогичный результат).
- Все готово, мы получили модули всех значений в исходном столбце.
Заключение
Таким образом, в Эксель можно легко и быстро посчитать модуль числа с помощью специально предназначенной для этого функции. Причем ввиду того, что формула достаточно проста и содержит всего один аргумент, ее можно сразу писать в ячейке таблицы. Или же можно воспользоваться мастером функций, который позволит безошибочно выполнить расчет.
6.2.4. Модуль числа
Автор Татьяна Андрющенко На чтение 2 мин.
Модулем числа а (записывают |a|) называют расстояние от начала отсчета до точки, соответствующей данному числу а.
Значение модуля любого числа неотрицательно. |3|=3; |-3|=3, т.к. расстояние от начала отсчета и до числа -3, и до числа 3 равно трем единичным отрезкам. Противоположные числа имеют равные модули. Модуль нуля равен нулю: |0|=0.
По определению модуля числа: |a|=a, если a≥0 и |a|=-a, если а<0. Читают: модуль неотрицательного числа равен самому этому числу; модуль отрицательного числа равен противоположному числу.
Примеры.
1. Вычислить: а) |5|-2; б) |-12| : 6; в) |-24| + |13|; г) |65|-|-45|.
Решение. а) |5|-2=5-2=3;
б) |-12| : 6=12 : 6=2;
в) |-24|+|13|=24+13=37;
г) |65|-|-45|=65-45=20.
2. Решить уравнение: а) |m|+4=10; б) 6-|x|=2.
Решение.
а) |m|+4=10;
|m|=10-4; из суммы вычли известное слагаемое;
|m|=6. Так как |-6|=6 и |6|=6, то m=-6 или m=6.
Ответ: -6; 6.
б) 6-|x|=2.
|x|=6-2;
|x|=4, отсюда х=-4 или х=4.
Ответ: -4; 4.
3. Записать перечислением элементов множество целых чисел А, модуль которых меньше числа 5.
Решение. По определению модуля числа 5 искомые числа должны отстоять от начала отсчета как вправо, так и влево на расстояние, меньшее пяти единичных отрезков. В этом промежутке (показан штриховкой на рисунке) бесконечно много чисел, но нам нужно выбрать из них лишь все целые числа.
Ответ: множество А={-4, -3, -2, -1, 0, 1, 2, 3, 4}.
4. Записать перечислением множество натуральных чисел В, модуль которых меньше числа 5.
Решение. Из всех чисел, показанных на рисунке штриховкой, нам нужно выбрать натуральные, т.е. только те числа, которые употребляются при счете предметов. Ответ: B={1, 2, 3, 4}.
Как вычислить модуль скорости
Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько стремительно тело передвигается в пространстве. Перемещение полагает метаморфоза координат.
Инструкция
1. Введите систему координат, касательно которой вы будете определять направление и модуль скорости .
2. По имеющейся функции зависимости скорости от времени дозволено обнаружить значение скорости в всякий момент времени t. Пускай, скажем, v=2t?+5t-3. Если требуется обнаружить модуль скорости в момент времени t=1, примитивно подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.
3. Когда задача требует обнаружить скорость в исходный момент времени, подставьте в функцию t=0. Таким же образом дозволено обнаружить время, подставив вестимую скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t?+5t-3=0. Отсель t=[-5±?(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а от того что время не может быть негативным, остается только t=1/2.
4. Изредка в задачах уравнение скорости дается в завуалированной форме.
5. Помимо откровенного движения тела, существует еще и движение тела по окружности. В всеобщем случае оно является криволинейным. Тут появляется центростремительное убыстрение, которое связано с линейной скоростью формулой a(c)=v?/R, где R – радиус. Комфортно рассматривать также угловую скорость ?, причем v=?R.
Модуль числа n представляет собой число единичных отрезков от начала координат до точки n.
Инструкция
1. Модуль числа также принято называть безусловной величиной этого числа . Он обозначается короткими вертикальными линиями, проведенными слева и справа от числа . Скажем, модуль числа 15 записывается дальнейшим образом: |15|.
2. Помните, что модуль может быть только позитивным числом либо нулем. Модуль позитивного числа равен самому числу. Модуль нуля равен нулю. То есть для всякого числа n, которое огромнее либо равно нулю, будет объективна дальнейшая формула |n| = n. Скажем, |15| = 15, то есть модуль числа 15 равен 15-ти.
3. Модулем негативного числа будет то же число, но с противоположным знаком. То есть для всякого числа n, которое поменьше нуля, будет объективна формула |n| = -n.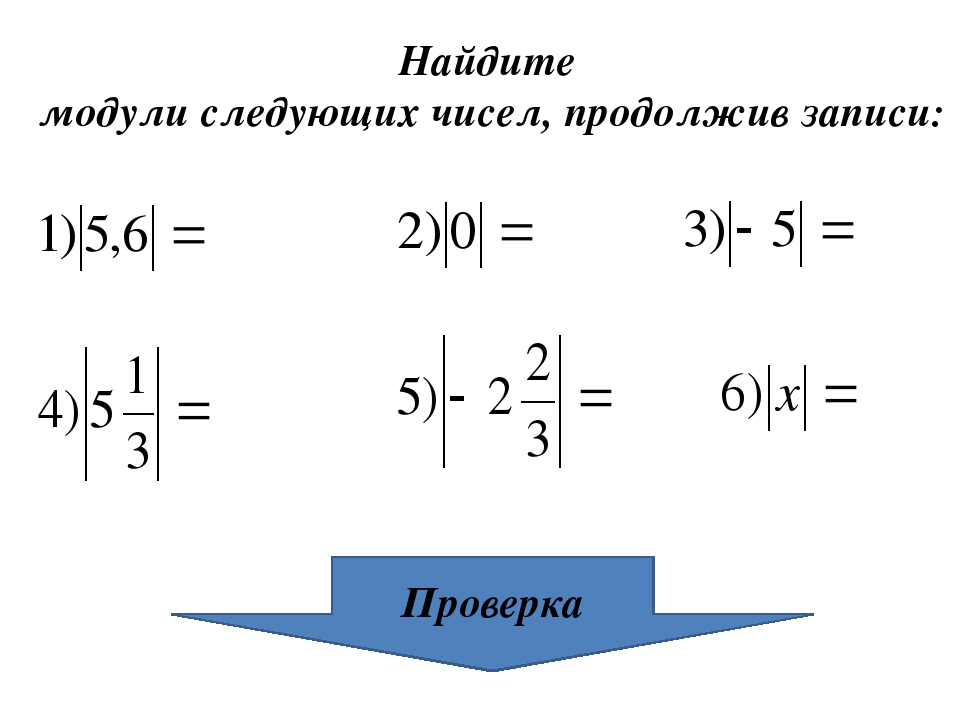
4. Дозволено находить модули не только для целых, но и для дробных чисел. Причем в отношении дробных чисел действуют те же правила. Скажем, |0,25| = 25, то есть модуль числа 0,25 будет равен 0,25. А |-?| = ?, то есть модуль числа -? будет равен ?.
5. При работе с модулями пригодно знать, что модули противоположных чисел неизменно равны друг другу, то есть |n| =|-n|. Это является основным свойством модулей. Скажем, |10| = |-10|. Модуль числа 10 равен 10-ти, верно так же, как модуль числа -10. Помимо того, |a – b| = |b – a|, потому что расстояние от точки a до точки b и расстояние от b до a равны друг другу. Скажем, |25 – 5| = |5 – 25|, то есть |20| = |- 20|.
Для нахождения метаморфозы скорости определитесь с типом движения тела. В случае если движение тела равномерно, изменение скорости равно нулю.
Вам понадобится
- секундомер, спидометр, радар, рулетка, акселерометр.
Инструкция
1. Определение метаморфозы скорости произвольно движущегося по прямой траекторииС поддержкой спидометра либо радара измерьте скорость тела в начале и конце отрезка пути. После этого от финального итога отнимите первоначальный, это и будет изменение скорости тела.
2. Определение метаморфозы скорости тела, движущегося с ускорениемНайдите убыстрение тела. Используйте акселерометр либо динамометр. Если знаменита масса тела, тогда силу, действующую на тело, поделите на его массу (a=F/m). Позже этого измерьте время, за которое происходил процесс метаморфозы скорости .

3. Определение метаморфозы скорости тела при поворотеЕсли изменилась не только величина, но и направление скорости , то обнаружьте ее изменение через векторную разность исходной и финальной скорости . Для этого измерьте угол между векторами. После этого от суммы квадратов скоростей отнимите удвоенное их произведение, умноженное на косинус угла между ними: v1?+v2?-2v1v2•Cos(?). Из полученного числа извлеките квадратный корень.
Видео по теме
Для определения скорости разных видов движения потребуются различные формулы. Дабы определить скорость равномерного движения, расстояние поделите на время его прохождения. Среднюю скорость движения находите сложением всех отрезков, которое прошло тело, на всеобщее время движения. При равноускоренном движении узнайте убыстрение, с которым двигалось тело, а при свободном падении высоту, с которой оно предисловие движение.
Вам понадобится
- дальномер, секундомер, акселерометр.
Инструкция
1. Скорость равномерного движения и средняя скоростьИзмерьте расстояние с поддержкой дальномера, которое прошло тело, а время, за которое оно его одолело, с поддержкой секундомера. Позже этого поделите расстояние, пройденное телом на время его прохождения, итогом будет скорость равномерного движения (v=S/t). Если тело движется неравномерно, произведите те же измерения и примените ту же формулу – тогда получите среднюю скорость тела. Это значит, что если бы тело по данному отрезку пути двигалось с полученной скоростью, оно было бы в пути время, равное измеренному. Если тело движется по окружности, измерьте ее радиус и время прохождения полного цикла, после этого радиус умножьте на 6,28 и поделите на время (v=6,28•R/t). Во всех случаях итог получится в метрах в секунду. Для перевода в километры в час помножьте его на 3,6.
2. Скорость равноускоренного движенияИзмерьте убыстрение тела с поддержкой акселерометра либо динамометра, если знаменита масса тела.
3. Скорость вольно падающего телаС поддержкой дальномера измерьте высоту, с которой падает тело в метрах. Дабы узнать скорость, с которой оно долетит до поверхности Земли (без контроля сопротивления воздуха), умножьте высоту на 2 и на число 9,81 (убыстрение свободного падения). Из итога извлеките квадратный корень. Дабы обнаружить скорость тела на всякий высоте, применяйте ту же методологию, только от исходной высоты, отнимайте нынешнюю и полученное значение подставляйте взамен высоты.
Видео по теме
Человек привык воспринимать представление “скорость ” как что-то больше примитивное, чем это есть на самом деле. Подлинно, проносящийся на перекрестке автомобиль движется с определенной скорость ю, в то время как человек стоит и отслеживает за ним.
Инструкция
1. Дозволено продолжить рассмотрение темы движущегося на перекрестка на автомобиле. Человек же, стоя на красном свете светофора, стоит и глядит на проезжающий автомобиль. Человек статичен, следственно примем его за систему отсчета. Система отсчета – такая система, касательно которой движется какое-нибудь тело либо другая физическая точка.
2. Возможен, автомобиль движется со скорость ю 50 км/ч. Но, возможен, что человек побежал следом автомобилю (дозволено, скажем, взамен автомобиля представить маршрутку либо проезжающий мимо автобус). Скорость бега человека 12 км/ч. Таким образом, скорость данного механического транспортного средства представится человеку не столь и стремительной, как было прежде, когда он стоял! В этом каждая и суть относительной скорости.
3. Дозволено разглядеть еще один живой пример. Довольно припомнить всякий из моментов, когда человек, сидя у окна автобуса, отслеживает за проносящимися мимо автомобилями. Подлинно, из окна автобуса их скорость кажется примитивно потрясающей. И это не изумительно, чай, если принять автобус за систему отсчета, то скорость автомобиля и скорость автобуса надобно будет сложить. Возможен, что автобус движется со скорость ю 50 км/ч, а машины 60 км/ч. Тогда 50 + 60 = 110 км/ч. Именно с такой скорость ю эти самые автомобили проносятся мимо автобуса и пассажиров в нем.Эта же скорость будет объективна и действительна и в том случае, если за систему отсчета принять всякий из проезжающих мимо автобусов автомобилей.
Кинематика постигает разные виды движения тела с заданной скоростью, направлением и траекторией. Дабы определить его расположение касательно точки начала пути, надобно обнаружить перемещение тела .
Инструкция
1. Движение тела происходит по некоторой траектории. В случае откровенного движения ею является прямая линия, следственно обнаружить перемещение тела достаточно примитивно: оно равно пройденному пути. В отвратном случае определить его дозволено по координатам исходного и финального расположения в пространстве.
2. Величина перемещения физической точки является векторной, от того что она имеет направление. Следственно, дабы обнаружить ее числовое значение, нужно вычислить модуль вектора, соединяющего точки начала пути и его окончания.
3. Разглядим двухмерное координатное пространство. Пускай тело проделало путь от точки A (x0, y0) до точки B (x, y).
4. Модуль вектора, т.е. длина перемещения тела , в свою очередь, является гипотенузой этого треугольника, длину которой легко определить по теореме Пифагора. Он равен квадратному корню из суммы квадратов проекций:S = ?(Sx? + Sy?).
5. В трехмерном пространстве:S = ?(Sx? + Sy? + Sz?), где Sz = z – z0.
6. Это формула является всеобщей для всякий разновидности движения. Вектор перемещения владеет несколькими свойствами: • его модуль не может превышать длину пройденного пути;• проекция перемещения может быть как позитивной, так и негативной величиной, в то время как величина пути неизменно огромнее нуля;• в всеобщем случае перемещение не совпадает с траекторией движения тела , а его модуль не равен пути.
7. В частном случае откровенного движения тело перемещается только по одной оси, скажем, оси абсцисс. Тогда длина перемещения равна разности финальной и исходной первой координаты точек:S = x – x0.
От модуля исходной скорости во многом зависят колляции движения тела. Для того дабы обнаружить эту величину, нужно воспользоваться дополнительными измерениями либо данными. Величина модуля исходной скорости может являться основополагающей колляцией, скажем, для огнестрельного оружия.
Вам понадобится
- – рулетка;
- – дальномер;
- – секундомер;
- – акселерометр;
- – спидометр;
- – угломер;
- – хронограф.
Инструкция
1. Вначале определитесь с типом движения. Если оно равномерное, то довольно измерить длину пути, по которому переместилось тело, сделав это рулеткой, дальномером либо иным доступным методом, и поделить это значение на время, за которое это перемещение осуществлялось.
2. При равноускоренном откровенном движении измерьте при помощи акселерометра убыстрение тела, а с подмогой секундомера время его движения, спидометром финальную скорость в конце отрезка пути. Обнаружьте значение модуля исходной скорости, отняв от финальной скорости произведение убыстрения на время движения v0=v-a*t. Если незнакомо значение убыстрения, измеряйте расстояние, которое покрыло тело за время t. Сделайте это при помощи рулетки либо дальномера.
3. Зафиксируйте значение финальной скорости. Обнаружьте исходную скорость, отняв от удвоенного значения расстояния S, поделенного на время, значение финальной скорости v, v0=2S/t-v. Когда значение финальной скорости измерить трудно, а убыстрение знаменито, воспользуйтесь иной формулой. Для этого измеряйте перемещение тела, а также время, которое оно было в пути.
4. Когда тело начинает движение под углом к горизонту, на него воздействует сила тяжести. Для того дабы обнаружить модуль исходной скорости, при помощи угломера замеряйте угол к горизонту, под которым тело начинает двигаться. При помощи рулетки либо дальномера замеряйте расстояние, на котором тело упадет на поверхность земли. Дабы определить модуль исходной скорости, расстояние S поделите на синус удвоенного угла ?. Из полученного итога извлеките квадратный корень, v0=?(S/sin(2?)).
5. Дабы измерить модуль исходной скорости пули, выпущенной из стрелкового оружия, используйте хронограф. Для этого установите его так, как указано в его инструкции, от того что хронографы бывают различных типов. Позже этого сделайте выстрел из оружия, на табло хронографа появится итог. Выстрелите еще несколько раз и возьмите среднее значение показаний хронографа.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора — вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами — единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? «Наверное какой-то жуткий», подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему «механика твердых тел». А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.
Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.
Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости.
Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.
Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.
Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.
Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути соответствующее малому вектору по которому определяется вектор скорости. Вспомним, что Знак указывает
направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.
Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения
Здесь является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.
Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение определяет угол наклона а касательной на этом графике.
Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.
Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.
Модуль числа. Простое уравнение с модулем. Корень уравнения с модулем.
Наиболее часто возникают ошибки при решении уранений с модулем.
(|a|) — читается как модуль числа (a).
Определение модуля:
Модуль числа (|-5|) из определения является расстоянием от (-5) до (0).
- Если модуль числа равен положительному значению, то уравнение имеет два корня.
- Если модуль числа равен нулю, то уравнение имеет один корень.
- Если модуль равен отрицательному значению, то уравнение не имеет корней.
Пример 1. Решите (|x|=3)
Решение:
(|x|=3)
(x = 3) или (x = -3)
Уранение имеет два корня
Ответ: (x = 3) или (x = -3).
Пример 2. Решите (|x|=0)
Решение:
(|x|=0)
(x = 0)
Уравнение имеет один корень
Ответ: (x = 0).
Пример 3. Решите (|x|=-3)
Решение:
Модуль не может быть равен отрицательному значению!!!
корней нет
Ответ: корней нет.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявку
Репетитор по математике
Новосибирский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов.
Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
Оставить заявку
Репетитор по математике
Крымский федеральный университет им.
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-4 классов.
Я люблю математику потому, что в ней всё
подчиняется определенным правилам, которые легко понять и которые одинаковы абсолютно для всех. Математика имеет свои неизменные законы, которые действуют во все времена и во всех странах.
Со мной , Ваш ребенок, не будет получать скучные знания в душных кабинетах, а с удовольствием проведёт досуг познания «царицы наук» в игровой форме, не выходя из зоны комфорта , ведь математика — это весело !
Со мной будет интересно , обещаю ; )
Оставить заявку
Репетитор по математике
Барнаульский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Придерживаюсь знаменитых слов Ломоносова В.
Мои ученики – девятиклассники успешно сдают ОГЭ. А ребята младших классов повышают свои успехи в изучении интересной, но сложной науки «Математика». Направления моей педагогической деятельности:
-Систематизация и совершенствование знаний при изучении математики для улучшения успеваемости по предмету, при подготовки к школе : развитие внимания, логического мышления, изучение основных понятий математики для поступления в школу.
-Ликвидация пробелов изучения математики у учащихся и непонимания тем, помощь в выполнении домашних заданий.
-Подготовка к ОГЭ и ВПР по математике.
Решение уравнений
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Записаться на бесплатный урок
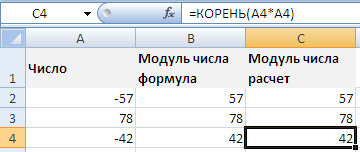
Модуль числа в Excel.

Модуль в Excel можно легко посчитать с помощью встроенных инструментов. Процедура не сложная, поэтому не займет много времени, а выполнить ее можно, используя функцию ABS. Также допускаются и некоторые альтернативные способы, которые будут рассмотрены ниже.
Принцип нахождения с помощью функции ABS
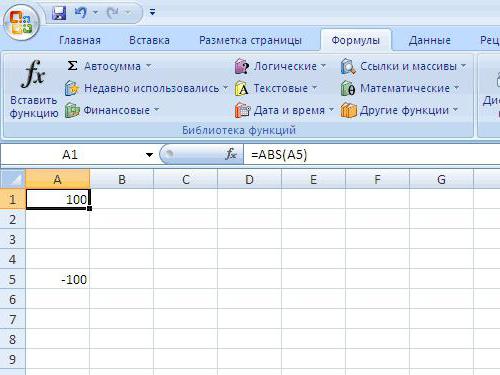
Модуль — это абсолютная величина. То есть, если необходимо найти его от числа -46, то ответ будет — 46 без знака минус. Но чтобы найти значение более сложных выражений, которое посчитать быстро в уме проблематично, можно воспользоваться функцией ABS. Стоит отметить, что данный инструмент работает во всех версиях Microsoft Office. Рассмотрим принцип ее работы на примере программы 2016 года выпуска. Обозначение синтаксиса данной программы: =АBS (число). Но знания этой аббревиатуры недостаточно, главное правильно применить ее на практике.
- Откройте программу Microsoft Excel, на пустом листе в одной из ячеек пропишите число, от которого необходимо найти модуль.
Предположим, это -12.
1
- Теперь подставьте в эту же ячейку формулу, а в скобки внесите заявленное число. Посмотрите, как это должно выглядеть, на скриншоте.
2
- После того, как прописали необходимые обозначения, нажмите кнопку «Enter» на клавиатуре. Вследствие этого отрицательное значение числа изменится на положительное.
Обратите внимание! Для того чтобы расчет функции получился правильным, необходимо использовать при вводе строго латинские буквы. В противном случае система будет выдавать ошибку.
Если вы планируете найти значение модуля в отдельно стоящей ячейке по отношению к той, где установлено отрицательное число, то в формуле вместо самого числа нужно будет прописать адрес необходимого окошка.
Еще один способ, который можно использовать для расчета модуля, он подойдет тем пользователям, которые не готовы запоминать множество цифр и формул, а полагаются лишь на алгоритмы электронной книги Microsoft Excel.
- Открываем программу и кликаем по той ячейке, в которой необходимо будет отобразить результат расчетов. Затем в этом месте делаем клик ПКМ и вызываем контекстное меню. В нем выбираем «Вставить функцию». Если такого обозначения нет, тогда переходим во вкладку «Формулы» и прямо в верхнем левом углу находим необходимый нам инструмент.
3
- Перед нами открывается окно «Вставка функции», здесь в выпадающем списке выбираем «Математические» и находим «ABS». В конце нажимаем на кнопку «ОК».
4
- Появляется следующее окошко, которое называется «Аргументы функции». Здесь нам необходимо в поле «Число» прописать значение, которое нужно использовать для нахождения модуля. У нас это число с минусом (-16). Жмем кнопку «ОК».
5
Совет! Кнопку «ОК» можно не нажимать, так как результат значения сразу видно в диалоговом окне. При закрытии «Аргументов функции» мы можем заметить, что выбранное нами число из отрицательного превратилось в положительное.
Соответственно, можно считать, что способ нахождения математического модуля выполнен верно.
Как найти модуль для нескольких чисел одновременно
Предположим, что у вас есть таблица с отрицательными числовыми значениями. Чтобы найти их модуль, необходимо сделать следующее.
- Имея четко сформированную таблицу, в ячейке, в которой необходимо найти модуль, делаем клик мышью, затем перемещаемся в строку для записи формул.
6
- Перед отрицательным числом прописываем знак равенства и устанавливаем функцию ABS, как это было выполнено на примере выше. Можем прописать вручную, чтобы было наглядно понятно, что имеется в виду. По итогу жмем кнопку «Enter», чтобы получить значение.
7
- Мы видим, что число изменило свой знак, соответственно, функция применилась корректно. Теперь, чтобы найти модуль для оставшихся цифр, нам необходимо взять границу ячейки и протянуть ее по всему диапазону, в котором присутствуют численные значения, чтобы использовать маркер автозаполнения.
8
Обратите внимание! Большинство пользователей прописывают формулу для нахождения модуля с вот такими знаками I-16I, причем еще и записывают их в скобки. Вместо корректного результата в таком случае появятся только ошибки, так как система программы Microsoft Excel независимо от версии документа не понимает подобный синтаксис.
Нахождение модуля с помощью функции «Корень»
Функция «Корень» в Excel тоже идеально подходит для нахождения модуля числа. Так как в офисной программе применяется понятие вычисления арифметического корня, то подходит он только для четных степеней. Соответственно, нечетные числа найдены не будут.
Другими словами, если мы найдем корень от числа, предварительно возведенного в квадрат, то сможем найти четную абсолютную величину, это и будет значение модуля.
Альтернативное нахождение с помощью функции «Знак»
Данный метод принято считать самым простым, так как он не требует углубленных знаний интерфейса программы.
Подведем итоги
На самом деле самостоятельное нахождение модуля одного числа выполнить быстрее и легче. А вот при использовании обширных таблиц и оперировании большим количеством данных незаменимым будет именно Microsoft Excel. Обращаем внимание, что в различных версиях программы возможны отличия в шагах при выполнении алгоритмов по нахождению величин.
Оцените качество статьи. Нам важно ваше мнение:
python — как получить путь к модулю?
Я также попробую ответить на несколько вариантов этого вопроса:
- поиск пути вызываемого скрипта
- поиск пути к исполняемому в данный момент скрипту
- поиск каталога вызываемого скрипта
(Некоторые из этих вопросов были заданы на SO, но были закрыты как дубликаты и перенаправлены сюда.)
Предостережения при использовании
__file__
Для импортированного модуля:
импортировать что-нибудь
что-нибудь. __файл__
__файл__
вернет абсолютный путь модуля. Однако, учитывая следующий сценарий foo.py:
# foo.py
напечатать '__file__', __file__
Вызов его с помощью «python foo.py» вернет просто «foo.py». Если добавить shebang:
#! / Usr / bin / python
# foo.py
напечатать '__file__', __file__
и вызовите его с помощью ./foo.py, он вернет ./foo.py. Вызов его из другого каталога (например, поместите foo.py на панели каталогов), затем вызовите
бар Python / foo.py
или добавление shebang и непосредственное выполнение файла:
бар / foo.py
вернет bar / foo.py (относительный путь ).
Поиск справочника
Теперь, перейдя оттуда, чтобы получить каталог, os.path.dirname (__ file__) также может быть сложным. По крайней мере, в моей системе он возвращает пустую строку, если вы вызываете ее из того же каталога, что и файл.бывший.
# foo.py
импорт ОС
print '__file__ is:', __file__
напечатайте 'os.path.dirname (__ file__) is:', os.path.dirname (__ file__)
выведет:
__file__ is: foo.py
os.path.dirname (__ file__):
Другими словами, он возвращает пустую строку, поэтому это не кажется надежным, если вы хотите использовать ее для текущего файла (в отличие от файла импортированного модуля). Чтобы обойти это, вы можете заключить его в вызов abspath:
# foo.ру
импорт ОС
напечатайте 'os.path.abspath (__ file__) is:', os.path.abspath (__ file__)
print 'os.path.dirname (os.path.abspath (__ file__)) is:', os.path.dirname (os.path.abspath (__ file__))
, который выводит что-то вроде:
os.path.abspath (__ file__): /home/user/bar/foo.py
os.path.dirname (os.path.abspath (__ file__)): / home / user / bar
Обратите внимание, что abspath () НЕ разрешает символические ссылки. Если вы хотите это сделать, используйте вместо этого realpath (). Например, создание символической ссылки file_import_testing_link, указывающей на file_import_testing.py, со следующим содержанием:
импорт ОС
напечатайте 'abspath (__ file __)', os.path.abspath (__ file__)
напечатать 'realpath (__ file __)', os.path.realpath (__ file__)
При выполнении
будут напечатаны абсолютные пути, например:
abspath (__ файл__) / home / user / file_test_link
реальный путь (__ файл__) /home/user/file_test.py
file_import_testing_link -> file_import_testing.py
Использование inspect
@SummerBreeze упоминает использование модуля проверки.
Кажется, это хорошо работает и довольно кратко для импортированных модулей:
импорт ОС
импортная инспекция
print 'inspect.getfile (os) is:', inspect.getfile (os)
послушно возвращает абсолютный путь. Для поиска пути к исполняемому в данный момент скрипту:
inspect.getfile (inspect.currentframe ())
(спасибо @jbochi)
Путь
— Python не может найти мой модуль
По сути, при выполнении сценария .py напрямую, он не знает, что он является частью подмодуля src , и не знает, где может быть модуль с именем src . Это имеет место либо в Python 2, либо в 3.
Как вы знаете, Python находит модули на основе содержимого sys.path . Чтобы импортировать любой модуль, он должен находиться либо в каталоге, который указан в sys.path , либо в том же каталоге, что и сценарий, который вы запускаете.
Когда вы говорите python src / scripts / script.py , sys.path включает Project / src / scripts / (потому что там находится script.py ), но не Project . Поскольку Project не указан в пути, модули в этом каталоге ( src ) не могут быть импортированы.
Чтобы исправить это:
Я предполагаю, что ваш script.py является точкой входа для вашего модуля src (например, может быть, это основная программа). Если это правда, то вы можете исправить это, переместив скрипт .py до того же уровня, что и src :
Проект
├───.git
├───venv
| ───script.py <--- script.py перемещается сюда
└───src
├───__init __. Py
└───модули
├───__init __. Py
├───module1.py
└───module2.py
Таким образом, script.py может свободно импортировать что угодно в src , но ничто в src не может импортировать script.py .
Если дело не в том, и скрипт .py действительно является частью src , вы можете использовать аргумент python -m для выполнения script.py как часть модуля src , например:
$ python -m src.scripts.script
Поскольку вы указали python, какой модуль вы используете ( src ), он будет в пути. Итак, script.py будет знать, что это подмодуль src , а затем сможет импортировать из src .
Будьте осторожны в этой ситуации — существует вероятность создания циклического импорта, если что-то в src импортирует src.scripts.script .
В качестве альтернативы обоим этим подходам вы можете изменить sys.path непосредственно в script.py :
импортная система
sys.path.insert (0, '/ path / to / Project') # расположение src
Хотя это работает, я обычно не предпочитаю это. Для этого требуется script.py , чтобы точно знать, как устроен ваш код, и может вызвать путаницу при импорте, если другая программа python когда-либо попытается импортировать сценарий .py .
Где Python ищет модули? — Функциональные методы МРТ
( newcommand {L} [1] { | # 1 |} newcommand {VL} [1] { L { vec {# 1}}} newcommand {R} [ 1] { operatorname {Re} , (# 1)} newcommand {I} [1] { operatorname {Im} , (# 1)} )
См .:
Допустим, мы написали модуль Python и сохранили его как a_module.py в
каталог под названием код .
У нас также есть сценарий a_script.py в каталоге с именем
скриптов .
Мы хотим иметь возможность импортировать код из a_module.py для использования в
a_script.py . Итак, мы хотим, чтобы его линия была в
a_script.py :
Модуль и сценарий могут выглядеть так:
Содержимое code / a_module.py
def func ():
print ("Запуск полезной функции")
Содержимое скриптов / a_script.py
import a_module a_module.func ()
На данный момент a_script.py завершится ошибкой:
$ скриптов python3 / a_script.py
Отслеживание (последний вызов последний):
Файл "scripts / a_script.py", строка 1, в
импортировать a_module
ModuleNotFoundError: нет модуля с именем 'a_module'
Когда Python достигает строки import a_module , он пытается найти пакет или
модуль называется a_module . Пакет — это каталог, содержащий модули, но
пока мы будем рассматривать только модули. Модуль — это файл с соответствующим
расширение, например .py . Итак, Python ищет файл a_module.py ,
и не нашел.
Вы увидите тот же эффект в интерактивной консоли Python или в
IPython:
>>> импортировать a_module Отслеживание (последний вызов последний): Файл "", строка 1, в ModuleNotFoundError: нет модуля с именем 'a_module'
Python ищет модули в «sys.path»
Python имеет простой алгоритм поиска модуля с заданным именем, например
а_модуль .Он ищет файл с именем a_module.py в каталогах.
перечислено в переменной sys.path .
>>> import sys >>> тип (sys.path) <список классов> >>> для пути в sys.path: ... печать (путь) ... / Пользователи / brettmz-admin / dev_trees / mental-214-fall-2016 / sphinxext /usr/local/Cellar/python/3.7.2_1/Frameworks/Python.framework/Versions/3.7/lib/python37.zip /usr/local/Cellar/python/3.7.2_1/Frameworks/Python.framework/Versions/3.7/lib/python3.7 /usr/local/Cellar/python/3.7.2_1/Frameworks/Python.framework/Versions/3.7/lib/python3.7/lib-dynload /Users/brettmz-admin/Library/Python/3.7/lib/python/site-packages / Пользователи / brettmz-admin / dev_trees / grin / Пользователи / brettmz-admin / dev_trees / rmdex /usr/local/lib/python3.7/site-packages
Файл a_module.py находится в каталоге code , и этот каталог
нет в списке sys.path .
Поскольку sys.path — это просто список Python, как и любой другой, мы можем сделать
импортировать работу, добавив в список каталог с кодом .
>>> import sys
>>> sys.path.append ('код')
>>> # Теперь импорт будет работать
>>> импортировать a_module
Существуют различные способы убедиться, что каталог всегда находится на Python.
sys.path список при запуске Python, включая:
В качестве грубого взлома вы также можете поместить свой каталог с кодом на Python
sys.path вверху нужных файлов:
Содержимое скриптов / a_script_with_hack.py
import sys
sys.path.append ('код')
импортировать a_module
a_module.func ()
Тогда:
$ скриптов python3 / a_script_with_hack.py Запуск полезной функции
Простое добавление выше будет работать только при запуске сценария из
каталог, содержащий подкаталог с кодом . Например:
$ mkdir another_dir
$ cd another_dir
$ python3 ../scripts/a_script_with_hack.py
Отслеживание (последний вызов последний):
Файл "../scripts/a_script_with_hack.py ", строка 4, в
импортировать a_module
ModuleNotFoundError: нет модуля с именем 'a_module'
Это связано с тем, что каталог с кодом , который мы указали, является относительным путем,
и поэтому Python ищет каталог code в текущем рабочем
каталог.
Чтобы взлом работал при запуске кода из любого каталога, вы можете использовать
некоторые манипуляции с путями в переменной «__file__»:
Содержимое скриптов / a_script_with_better_hack.py
из os.path import dirname, abspath, join import sys # Найти каталог кода относительно нашего каталога THIS_DIR = имя каталога (__ file__) CODE_DIR = abspath (присоединиться (THIS_DIR, '..', 'code')) sys.path.append (CODE_DIR) импортировать a_module a_module.func ()
Теперь импорт модуля работает из another_dir :
$ python3 ../scripts/a_script_with_better_hack.py Запуск полезной функции
Как Python находит пакеты? // Ли о кодировании // Мой блог о кодировании и прочем.
Я просто столкнулся с ситуацией, когда я скомпилировал и установил Python 2.7.9 из исходного кода на Ubuntu, но Python не смог найти пакеты, которые я ранее установил. Это, естественно, поднимает вопрос — откуда Python знает, где искать пакеты, когда вы вызываете import ? Этот пост относится конкретно к Python 2.7.9, но я предполагаю, что Python 3x работает очень похоже.
В этом посте я сначала опишу, как Python находит пакеты, а затем я закончу своим открытием, касающимся Python по умолчанию, который поставляется с Ubuntu, и того, чем он отличается от обычного Python тем, как он находит пакеты.
системный путь
Импорт
Python работает путем поиска в каталогах, перечисленных в sys.path .
Используется Ubuntu 14.04 по умолчанию Python:
> импорт системы > напечатать ' n'.join (sys.path) /usr/lib/python2.7 /usr/lib/python2.7/plat-x86_64-linux-gnu /usr/lib/python2.7/lib-tk /usr/lib/python2.7/lib-old /usr/lib/python2.7/lib-dynload /usr/local/lib/python2.7/dist-packages /usr/lib/python2.7/dist-packages
Итак, Python найдет все пакеты, которые были установлены в эти места.
Как заполняется sys.path
Как объясняется в документации, sys.path заполняется с использованием
текущий рабочий каталог, за которым следуют каталоги, перечисленные в переменной среды PYTHONPATH ,
за которыми следуют зависящие от установки пути по умолчанию, которые контролируются модулем site .
Подробнее о sys.path можно прочитать в документации Python.
Если ваша переменная среды PYTHONPATH не установлена, sys.путь будет состоять из текущего рабочего каталога плюс
любые манипуляции с ним со стороны модуля site .
Модуль сайта автоматически импортируется при запуске Python, вы можете узнать больше о том, как он управляет вашим
sys.path в документации Python.
Это немного сложно.
Вы можете манипулировать
sys.path
Вы можете управлять sys.path во время сеанса Python, и это изменит способ поиска модулей Python.Например:
import sys, os
# Это не сработает - нет приветственного модуля
импорт привет
Отслеживание (последний вызов последний):
Файл "", строка 1, в
ImportError: нет модуля с именем hi
# Создайте модуль hi в вашем домашнем каталоге.
home_dir = os.path.expanduser ("~")
my_module_file = os.path.join (домашний_каталог, "hi.py")
с open (my_module_file, 'w') как f:
f.write ('напечатайте "привет" n')
f.write ('a = 10 n')
# Добавить домашний каталог в sys.path
sys.path.append (домашний_каталог)
# Теперь это работает, и печатает привет!
импорт привет
распечатать привет.а
Модуль
__file__ атрибут
Когда вы импортируете модуль, вы обычно можете проверить атрибут __file__ модуля, чтобы узнать, где находится модуль в вашей файловой системе:
> импортировать numpy > numpy .__ file__ '/usr/local/lib/python2.7/dist-packages/numpy/__init__.pyc'
Однако в документах Python указано, что:
Атрибут файла отсутствует для модулей C, которые статически связаны с интерпретатором; для модулей расширения, динамически загружаемых из общей библиотеки, это путь к файлу общей библиотеки.
Так, например, это не работает:
> импорт системы > sys .__ file__ Отслеживание (последний вызов последний): Файл "", строка 1, в AttributeError: объект 'модуль' не имеет атрибута '__file__'
Логично, что модуль sys статически связан с интерпретатором — по сути, он является частью интерпретатора!
Модуль
imp
Python предоставляет всю систему import через модуль imp .Это довольно круто, что все это может быть подвергнуто злоупотреблениям, если мы захотим.
imp.find_module можно использовать для поиска модуля:
> импортный имп
> imp.find_module ('numpy')
(Нет, '/usr/local/lib/python2.7/dist-packages/numpy', ('', '', 5))
Вы также можете импортировать и произвольный исходный код Python как модуль, используя imp.load_source . Это тот же пример ранее,
except импортирует наш модуль, используя imp вместо того, чтобы манипулировать sys.путь :
import sys, os, imp
# Создайте модуль hi в вашем домашнем каталоге.
home_dir = os.path.expanduser ("~")
my_module_file = os.path.join (домашний_каталог, "hi.py")
с open (my_module_file, 'w') как f:
f.write ('напечатайте "привет" n')
f.write ('a = 10 n')
# Загружаем модуль hi с помощью imp
привет = imp.load_source ('привет', my_module_file)
# Теперь это работает, и печатает привет!
импорт привет
print hi.a # a равно 10!
print type (привет) # это модуль!
Передача 'hi' в imp.load_source просто устанавливает атрибут __name__ модуля.
Ubuntu Python
Теперь вернемся к проблеме отсутствия пакетов после установки новой версии Python, скомпилированной из исходников. Сравнивая
sys.path как из Ubuntu Python, который находится по адресу / usr / bin / python , так и из недавно установленного Python, который
находится по адресу / usr / local / bin / python , я мог бы разобраться:
Ubuntu Python (
/ usr / bin / python ):
>>> import sys >>> print ' n'.join (sys.дорожка) /usr/lib/python2.7 /usr/lib/python2.7/plat-x86_64-linux-gnu /usr/lib/python2.7/lib-tk /usr/lib/python2.7/lib-old /usr/lib/python2.7/lib-dynload /usr/local/lib/python2.7/dist-packages /usr/lib/python2.7/dist-packages
Python, скомпилированный из исходного кода (
/ usr / local / bin / python )
>>> import sys >>> print ' n'.join (sys.path) /usr/local/lib/python27.zip /usr/local/lib/python2.7 /usr/local/lib/python2.7/plat-linux2 /usr/local/lib/python2.7/lib-tk / usr / local / lib / python2.7 / старая библиотека /usr/local/lib/python2.7/lib-dynload /usr/local/lib/python2.7/site-packages
Оказалось, что для меня важно было dist-packages по сравнению с site-packages . Используя Python для Ubuntu, мои пакеты были установлены в /usr/local/lib/python2.7/dist-packages , тогда как новый Python, который я установил, ожидает, что пакеты будут установлены в /usr/local/lib/python2.7/ сайт-пакеты . Мне просто нужно было манипулировать переменной окружения PYTHONPATH , чтобы указать на dist-packages , чтобы получить доступ к ранее установленному пакету с недавно установленной версией Python.
Как Ubuntu манипулировал sys.path
?
Итак, как дистрибутив Python для Ubuntu знает, что нужно использовать /usr/local/lib/python2.7/dist-packages в sys.path ? Это жестко запрограммировано
в их сайт модуль! Сначала найдите, где находится код модуля сайта :
> импорт сайта > site .__ file__ '/usr/lib/python2.7/site.pyc'
Вот отрывок из Ubuntu Python site.py , который я просмотрел, открыв / usr / lib / python2.7 / site.py в текстовом редакторе. Сначала комментарий вверху:
Для Debian и производных этот sys.path дополнен каталогами
для пакетов, распространяемых внутри дистрибутива. Локальные дополнения идут
в / usr / local / lib / python / dist-packages, дополнения Debian
установить в / usr / {lib, share} / python / dist-packages.
/ usr / lib / python / site-packages не используется.
Хорошо, вот и все. Они объясняют, чем отличается дистрибутив Python для Debian.
А теперь для кода, реализующего это изменение:
def getsitepackages ():
"" "Возвращает список, содержащий все глобальные каталоги пакетов сайтов.
(и, возможно, сайт-питон).Для каждого каталога, присутствующего в глобальных PREFIXES, эта функция
найдет свой подкаталог `site-packages` в зависимости от системы
environment и вернет список полных путей.
"" "
sitepackages = []
видел = установить ()
для префикса в ПРЕФИКСАХ:
если не видно префикса или префикса:
Продолжать
visible.add (префикс)
если sys.platform в ('os2emx', 'riscos'):
sitepackages.append (os.path.join (префикс, "Lib", "site-packages"))
elif os.sep == '/':
sitepackages.append (os.path.join (префикс, "local / lib",
"python" + sys.version [: 3],
"dist-пакеты"))
sitepackages.append (os.path.join (префикс, "lib",
"python" + sys.version [: 3],
"dist-пакеты"))
еще:
sitepackages.append (префикс)
sitepackages.append (os.path.join (префикс, "lib", "site-packages"))
если sys.платформа == "дарвин":
# только для фреймворков * добавляем стандартный Apple
# местоположения.
из sysconfig import get_config_var
framework = get_config_var ("PYTHONFRAMEWORK")
если фреймворк:
sitepackages.append (
os.path.join ("/ Библиотека", framework,
sys.version [: 3], "сайты-пакеты"))
вернуть пакеты сайта
Это все есть, если ты достаточно сумасшедший, чтобы копать так глубоко.
Вверх
Find-Module (PowerShellGet) — PowerShell | Документы Microsoft
Находит в репозитории модули, соответствующие указанным критериям.
В этой статье
Синтаксис
Найти-модуль
[[-Название] <строка []>]
[-MinimumVersion <строка>]
[-MaximumVersion <строка>]
[-RequiredVersion <строка>]
[-Все версии]
[-IncludeDependencies]
[-Filter <строка>]
[-Tag <строка []>]
[-Включает <строка []>]
[-DscResource <строка []>]
[-RoleCapability <строка []>]
[-Команда <строка []>]
[-Прокси ]
[-ProxyCredential ]
[-Repository <строка []>]
[-Credential ]
[-AllowPrerelease]
[<Общие параметры>]
Описание
Командлет Find-Module находит в репозитории модули, которые соответствуют указанным критериям. Find-Module возвращает объект PSRepositoryItemInfo для каждого найденного модуля. Объекты могут быть
отправляется по конвейеру в командлеты, такие как Install-Module .
При первой попытке Find-Module использовать репозиторий вам может быть предложено установить обновления.
Если источник репозитория не зарегистрирован с помощью командлета Register-PSRepository , возникает ошибка
вернулся.
Find-Module возвращает последнюю версию модуля, если не используются параметры, ограничивающие
версия.Чтобы получить список версий модуля в репозитории, используйте параметр AllVersions .
Если указан параметр MinimumVersion , Find-Module возвращает версию модуля, которая
равно или больше минимального. Если в репозитории доступна более новая версия,
возвращается более новая версия.
Если указан параметр MaximumVersion , Find-Module возвращает самую новую версию
модуль, не превышающий указанную версию.
Если указан параметр RequiredVersion , Find-Module возвращает только версию модуля
это точное соответствие указанной версии. Find-Module выполняет поиск по всем доступным
модули, потому что могут возникнуть конфликты имен между источниками.
В следующих примерах галерея PowerShell используется как единственная
зарегистрированный репозиторий. Get-PSRepository отображает зарегистрированные репозитории. Если у вас несколько
для зарегистрированных репозиториев используйте параметр -Repository , чтобы указать имя репозитория.
Примеры
Пример 1. Найти модуль по имени
В этом примере выполняется поиск модуля в репозитории по умолчанию.
Найти модуль-имя PowerShellGet
Название версии Описание репозитория
------- ---- ---------- -----------
2.1.0 PowerShell Получить модуль PowerShell PSGallery с командами для обнаружения ...
Командлет Find-Module использует параметр Name для указания модуля PowerShellGet .
Пример 2: Найти модули с похожими именами
В этом примере используется подстановочный знак звездочка ( * ) для поиска модулей с похожими именами.
Найти-модуль-имя PowerShell *
Название версии Описание репозитория
------- ---- ---------- -----------
0.4.0 powershell-yaml PSGallery Модуль Powershell для сериализации и ...
2.1.0 PowerShell Получить модуль PowerShell PSGallery с командами для...
1.9 Powershell.Helper.Extension PSGallery # Powershell.Helper.Extension ...
3.1 PowerShellHumanizer PSGallery PowerShell Humanizer обертывает Humanizer ...
4.0 PowerShellISEModule PSGallery - модуль, расширяющий возможности ISE
.
Командлет Find-Module использует параметр Name со звездочкой ( * ) для поиска всех
модули, содержащие PowerShell .
Пример 3: Найти модуль с минимальной версией
В этом примере выполняется поиск минимальной версии модуля.Если в репозитории есть более новая версия
модуля возвращается более новая версия.
Find-Module -Name PowerShellGet -MinimumVersion 1.6.5
Название версии Описание репозитория
------- ---- ---------- -----------
2.1.0 PowerShell Получить модуль PowerShell PSGallery с командами для обнаружения ...
Командлет Find-Module использует параметр Name для указания модуля PowerShellGet .В
MinimumVersion указывает версию 1.6.5 . Find-Module возвращает версию PowerShellGet
2.1.0 , потому что она превышает минимальную версию и является самой последней версией.
Пример 4: Найти модуль по конкретной версии
В этом примере возвращается объект, представляющий конкретную версию модуля. Если указанная версия
не найден, возвращается ошибка.
Find-Module -Name PowerShellGet -RequiredVersion 1.6.5
Название версии Описание репозитория
------- ---- ---------- -----------
1.6.5 PowerShell Get PSGallery Модуль PowerShell с командами для обнаружения ...
Командлет Find-Module использует параметр Name для указания модуля PowerShellGet . В
Параметр RequiredVersion указывает версию 1.6.5 .
Пример 5: Найти модуль в определенном репозитории
В этом примере используется параметр Repository для поиска модуля в определенном репозитории.
Find-Module -Name PowerShellGet -Repository PSGallery
Название версии Описание репозитория
------- ---- ---------- -----------
2.1.0 PowerShell Получить модуль PowerShell PSGallery с командами для обнаружения ...
Командлет Find-Module использует параметр Name для указания модуля PowerShellGet . В
Repository Параметр указывает на поиск в репозитории PSGallery .
Пример 6: Найти модуль в нескольких репозиториях
В этом примере для указания репозитория используется Register-PSRepository . Find-Module использует
репозиторий для поиска модуля.
Register-PSRepository -Name MySource -SourceLocation https://www.myget.org/F/powershellgetdemo/
Найти-модуль-имя Contoso * -Repository PSGallery, MySource
Название версии репозитория Описание
---------- ------- ---- -----------
PSGallery 2.0.0.0 Командлеты ContosoServer и ресурсы DSC для управления сервером Contoso ...
MySource 1.2.0.0 Командлеты ContosoClient и ресурсы DSC для управления клиентом Contoso ...
Командлет Register-PSRepository регистрирует новый репозиторий. Параметр Name назначает
имя MySource . Параметр SourceLocation указывает адрес репозитория.
Командлет Find-Module использует параметр Name со звездочкой ( * ), чтобы указать
Модуль Contoso .Параметр Repository указывает на поиск в двух репозиториях, PSGallery
и MySource .
Пример 7: Найдите модуль, содержащий ресурс DSC
Эта команда возвращает модули, содержащие ресурсы DSC. Параметр включает имеет четыре
предопределенные функции, которые используются для поиска в репозитории. Используйте завершение табуляции, чтобы отобразить
четыре функции, поддерживаемые Включает параметр .
Find-Module -Repository PSGallery-Включает DscResource
Название версии Описание репозитория
------- ---- ---------- -----------
2.7.0 Carbon PSGallery Carbon - это модуль PowerShell ...
8.5.0.0 xPSDesiredStateConfiguration PSGallery Модуль xPSDesiredStateConfiguration ...
1.3.1 Управление пакетами PSGallery PackageManagement (a.k.a. OneGet) - это ...
2.7.0.0 Модуль xWindowsUpdate PSGallery с ресурсами DSC ...
3.2.0.0 xCertificate PSGallery Этот модуль включает ресурсы DSC ...
3.1.0.0 xPowerShellExecutionPolicy PSGallery Этот ресурс DSC может изменять пользователя...
Командлет Find-Module использует параметр Repository для поиска в репозитории PSGallery .
Параметр включает указывает DscResource , функциональность, которую параметр
можно искать в репозитории.
Пример 8: Найти модуль с фильтром
В этом примере для поиска модулей используется фильтр для поиска в репозитории.
Для репозитория на основе NuGet параметр Filter выполняет поиск по имени, описанию и
теги для аргумента.
Find-Module -Filter AppDomain
Название версии Описание репозитория
------- ---- ---------- -----------
1.0.0.0 AppDomainConfig PSGallery Управление конфигурацией AppDomain ...
1.1.0 ClassExplorer PSGallery Быстрый поиск классов в домене приложений ...
Командлет Find-Module использует параметр Filter для поиска в репозитории AppDomain .
Параметры
-AllowPrerelease
Включает в результаты модули, помеченные как предварительный выпуск.
Ложный подстановочный знак 908
| Тип: | SwitchParameter |
| Позиция: | Именованный |
| Значение по умолчанию: | Нет |
| Принять ввод конвейера: | Ложный |
-Все версии
Задает включение всех версий модуля в результаты.Вы не можете использовать AllVersions
с параметрами MinimumVersion , MaximumVersion или RequiredVersion .
Ложный подстановочный знак 908
| Тип: | SwitchParameter |
| Позиция: | Именованный |
| Значение по умолчанию: | Нет |
| Принять конвейерный ввод: | Ложный |
-Команда
Задает массив команд для поиска в модулях.Команда может быть функцией или рабочим процессом.
Ложь
| Тип: | Строка [] | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | Ложные символы подстановки |
-Credential
Задает учетную запись пользователя с правами на установку модуля для указанного поставщика пакетов или
источник.
True
| Тип: | PSCredential |
| Позиция: | Именованный |
| Значение по умолчанию: | Нет |
| Принять ввод конвейера: |
-DscResource
Задает имя или часть имени модулей, содержащих ресурсы DSC. На PowerShell
соглашения, выполняет поиск ИЛИ , когда вы указываете несколько аргументов.
Ложь
| Тип: | Строка [] | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | Ложные символы подстановки |
-Фильтр
Задает фильтр на основе синтаксиса поиска PackageManagement , зависящего от поставщика. Для NuGet
модулей, этот параметр эквивалентен поиску с использованием панели поиска в галерее PowerShell.
Веб-сайт.
| Тип: | Строка | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | Ложный | 908 |
-IncludeDependencies
Указывает, что эта операция включает все модули, которые зависят от модуля, указанного в
параметр Name .
Ложный подстановочный знак 908
| Тип: | SwitchParameter |
| Позиция: | Именованный |
| Значение по умолчанию: | Нет |
| Принять ввод конвейера: | Ложный |
-включает
Возвращает только те модули, которые включают определенные виды функций PowerShell. Например, вы
может захотеть найти только модули, которые включают DSCResource .Допустимые значения для этого
параметры следующие:
- Командлет
- DscResource
- Функция
- RoleCapability
Принять ввод конвейера:
| Тип: | String [] |
| Допустимые значения: | DscResource, Cmdlet, Function, RoleCapability |
| Позиция: | Именованное |
| Ложь | |
| Принимать подстановочные знаки: | Ложь |
-MaximumVersion
Задает максимальную или последнюю версию модуля для включения в результаты поиска. MaximumVersion и RequiredVersion нельзя использовать в одной команде.
Подстановочные символы
| Тип: | Строка | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять конвейерный ввод: | Истинные | 17 |
-Минимальная версия
Задает минимальную версию модуля для включения в результаты. Минимальная версия и
Требуемая версия не может использоваться в одной команде.
Подстановочные символы
| Тип: | Строка | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять конвейерный ввод: | Истинный | 17 |
-Имя
Задает имена модулей для поиска в репозитории.Список модулей, разделенных запятыми
имена принимаются. Подстановочные знаки принимаются.
| Тип: | Строка [] | |
| Позиция: | 0 | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | True | 908 Ложь |
-Прокси
Указывает прокси-сервер для запроса, а не подключение напрямую к Интернет-ресурсу.
| Тип: | Uri | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | Истинный | 17 908 |
-ProxyCredential
Задает учетную запись пользователя, имеющую разрешение на использование прокси-сервера, указанного в
Прокси параметр.
True
| Тип: | PSCredential |
| Позиция: | Именованный |
| Значение по умолчанию: | Нет |
| Принять ввод конвейера: |
-Репозиторий
Используйте параметр Repository , чтобы указать, в каком репозитории искать модуль.Используется, когда
зарегистрировано несколько репозиториев. Принимает список репозиториев, разделенных запятыми. Чтобы зарегистрировать
репозиторий, используйте Register-PSRepository . Для отображения зарегистрированных репозиториев используйте Get-PSRepository .
Ложь
| Тип: | Строка [] | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | Ложные символы подстановки |
-Required Версия
Задает точный номер версии модуля для включения в результаты. Обязательно Версия
не может использоваться в той же команде, что и MinimumVersion или MaximumVersion .
Подстановочные символы
| Тип: | Строка | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять конвейерный ввод: | Истинные | 17 |
-RoleCapability
Определяет массив возможностей ролей.
Ложь
| Тип: | Строка [] | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | Ложные символы подстановки |
-Тег
Задает массив тегов. Примеры тегов включают DesiredStateConfiguration , DSC ,
DSCResourceKit или PSModule .
Ложь
| Тип: | Строка [] | |
| Позиция: | Именованный | |
| Значение по умолчанию: | Нет | |
| Принять ввод конвейера: | Ложные символы подстановки |
Входы
Строка []
Строка
Uri
PSCredential
Выходы
PSRepositoryItemInfo
Find-Module создает объектов PSRepositoryItemInfo , которые могут быть отправлены по конвейеру командлетам
например, Install-Module .
Банкноты
Важно
С апреля 2020 года галерея PowerShell больше не поддерживает безопасность транспортного уровня (TLS).
версии 1.0 и 1.1. Если вы не используете TLS 1.2 или выше, вы получите сообщение об ошибке, когда
пытается получить доступ к галерее PowerShell. Используйте следующую команду, чтобы убедиться, что вы используете TLS
1,2:
[Net.ServicePointManager] :: SecurityProtocol = [Net.SecurityProtocolType] :: Tls12
Для получения дополнительной информации см.
объявление в
Блог PowerShell.
Основы модуля: TechWeb: Boston University
Модуль Пакет доступен в общем вычислительном кластере, что позволяет пользователям получать доступ к нестандартным инструментам или альтернативным версиям стандартных пакетов. Это также альтернативный способ настройки вашей среды в соответствии с требованиями определенных пакетов. При необходимости можно загружать и выгружать определенные модули. Команда модуля обеспечивается программным обеспечением Lmod, разработанным в Техасском центре вычислительных технологий.
Версия Python, доступная без загрузки модуля, является более старой версией (2.7.5), которая предназначена только для использования в системе. Загрузите модуль, чтобы использовать Python.
Содержание
Общие команды
| список модулей | Список загруженных в настоящее время модулей. |
| модуль доступен | Список доступных пакетов. |
| паук модуля | Список доступных пакетов в другом формате. |
| справка модуля [ файл модуля ] | Описание указанного модуля. |
| показать модуль [ файл модуля ] | Отображает информацию об указанном модуле, включая изменения среды, зависимости, версию программного обеспечения и путь. |
| загрузка модуля [ файл модуля ] | Загружает модуль или указывает, какие зависимости не были загружены. |
| выгрузка модуля [ файл модуля ] | Выгружает указанный модуль из среды. |
| модуль продувки | Выгружает все загруженные модули |
Дополнительную информацию можно найти на странице руководства модуля.
Примеры команд
список модулей
scc4% список модулей
В настоящее время нет загруженных файлов модулей.
модуль доступен
Список доступных пакетов.
scc4% модуль avail
--------------------------------- /share/module.7/bioinformatics --------- ------------------------
2brad_denovo / 2019-01-22_giteec5016 meshclust2 / 2.1.0
2brad_gatk / 2019-01-22_git1fcc9e8 металл / 08.02.2010
добавка / 1.3.0 металл / 25.03.2011 (D)
angsd / 0.923 metalge / 08.02.2010
annovar / 2018apr minimac2 / 2014-09-15
artemis / 18.0.3 minimac3 / 2.0.1
август / 3.3.2 minimac4 / 1.0.0
bamtools / 2.5.1 mirdeep2 / 0.1.0
bamutil / 1.0.14 mixcr / 3.0.3
basemount / 0.15.103.3011 mmap / 2018-04-07
basespace-cli / 0.8.12.590 morgan / 3.2
basespace-cli / 0.9.17 morgan / 3.4 (D)
basespace-cli / 0.10.8 (D) mosdepth / 0.2.6
байескан / 2,1 месяца / 1,35,0
bbmap / 38.16 multiqc / 1.6
bcbio / 1.1,1 ряженый / 3,23
Вы также можете искать пакеты по имени. Например, чтобы увидеть все версии «тензорного потока», вы можете выполнить поиск по слову «тензорный поток» или подстроке типа «тензор»,
scc4% тензор доступности модуля
--------------------------------- /share/module.7/machine-learning ------- -----------------------------------
тензорный поток / 1.12 тензорный поток / 1.13.1 тензорный поток / 1.15.0 (D) тензорный поток / 2.0.0
Где:
D: модуль по умолчанию
модуль паук
Список доступных пакетов в другом формате.
scc4% модуль паук
-------------------------------------------------- -------------------------------------------------- -------
Ниже приводится список модулей, доступных в настоящее время:
-------------------------------------------------- -------------------------------------------------- -------
2брад_деново: 2брад_деново / 2019-01-22_giteec5016
2brad_gatk: 2brad_gatk / 2019-01-22_git1fcc9e8
3д-лед: 3д-лед / 2.2,6
R: R / 3.0.0, R / 3.5.1, R / 3.6.0_intel-2018, R / 3.6.0, R / 3.6.1_intel-2019
добавка: примесь / 1.3.0
афни: афни / 17.0.18-омп, афни / 19.1.00-омп, афни / 19.1.00, афни / 2011-12-21.1014-xorg, афни / 2011-12-21.1014
янтарь: янтарь / 16
amgx: amgx / 2019-12-13_gitb3101ff
AmgX - это библиотека ядра решателя с ускорением на GPU, которая ускоряет линейный решатель с интенсивными вычислениями.
часть моделирования.
анаконда2: анаконда2 / 5.2.0
анаконда3: анаконда3 / 5.2.0
Вы также можете искать пакеты по имени. Например, чтобы увидеть все версии «тензорного потока», вы можете выполнить поиск по слову «тензорный поток» или подстроке типа «тензор»,
scc4% модуль тензор паука
-------------------------------------------------- -------------------------------------------------- -------
тензорный поток:
-------------------------------------------------- -------------------------------------------------- -------
Версии:
тензорный поток / 1.12
tenorflow / 1.13.1
tenorflow / 1.15.0
tenorflow / 2.0.0
-------------------------------------------------- -------------------------------------------------- -------
Для получения подробной информации о конкретном модуле «тензорного потока» (в том числе о том, как загрузить модули) используйте полное имя модуля.
Например:
$ module spider tensorflow / 2.0.0
-------------------------------------------------- -------------------------------------------------- -------
Справка по модулю
[
файл модуля ]
scc4% справка по модулю gcc
------------------------------------ Справка по конкретному модулю для "gcc / 8.3,0 "-------------------------------------
gcc 8.3.0: Коллекция компиляторов GNU (GCC)
Компиляторы C, C ++ и Fortran.
Для получения дополнительной информации о gcc, пожалуйста, посетите https://gcc.gnu.org/
Для удобства предусмотрены следующие переменные среды:
$ SCC_GCC_DIR - Каталог базового пакета
$ SCC_GCC_BIN - Каталог исполняемых файлов пакета
$ SCC_GCC_LIB - Каталог библиотек пакетов
$ SCC_GCC_LICENSE - Информация о лицензии пакета
Показать модуль
[
файл модуля ]
scc4% модуль показать gcc
-------------------------------------------------- -------------------------------------------------- -------
/ share / module.7 / программирование / gcc / 8.3.0.lua:
-------------------------------------------------- -------------------------------------------------- -------
помощь([[
gcc 8.3.0: Коллекция компиляторов GNU (GCC)
Компиляторы C, C ++ и Fortran.
Для получения дополнительной информации о gcc, пожалуйста, посетите https://gcc.gnu.org/
Для удобства предусмотрены следующие переменные среды:
$ SCC_GCC_DIR - Каталог базового пакета
$ SCC_GCC_BIN - Каталог исполняемых файлов пакета
$ SCC_GCC_LIB - Каталог библиотек пакетов
$ SCC_GCC_LICENSE - Информация о лицензии пакета
]])
whatis ("Имя: gcc")
whatis ("Версия: 8.3,0 ")
whatis ("Описание: Коллекция компиляторов GNU (GCC)")
whatis ("URL: https://gcc.gnu.org/")
whatis ("Категории: программирование")
whatis ("Ключевые слова: centos7, программирование, GNU, компилятор, c, c ++, fortran")
setenv ("SCC_GCC_DIR", "/ share / pkg.7 / gcc / 8.3.0 / install")
setenv ("SCC_GCC_BIN", "/ share / pkg.7 / gcc / 8.3.0 / install / bin")
setenv ("SCC_GCC_LIB", "/ share / pkg.7 / gcc / 8.3.0 / install / lib64")
setenv ("SCC_GCC_LIB32", "/ share / pkg.7 / gcc / 8.3.0 / install / lib")
setenv ("SCC_GCC_LICENSE", "/ share / pkg.7 / gcc / 8.3.0 / install / КОПИРОВАНИЕ ")
prepend_path («ПУТЬ», «/ share / pkg.7 / gcc / 8.3.0 / install / bin»)
prepend_path ("LD_LIBRARY_PATH", "/ share / pkg.7 / gcc / 8.3.0 / install / lib")
prepend_path ("LD_LIBRARY_PATH", "/ share / pkg.7 / gcc / 8.3.0 / install / lib64")
Сценарии и пакетные команды
Чтобы обеспечить правильную загрузку модулей в файле сценария, добавьте параметр -l в первую строку вашего сценария, то есть:
#! / Bin / bash -l
При включении модулей в сценарии и команды пакетной отправки (через qsub ) рекомендуется указывать модули и приложения по номеру версии.Со временем будут установлены новые версии приложений. Указание версий приложений гарантирует, что в будущем задания будут выполняться так же, как и сейчас.
Пример:
модуль нагрузки tophat / tophat-2.0.4_gnu446
вместо
Модуль нагрузки tophat
Автоматическая загрузка модулей
Модули
могут автоматически загружаться при входе в систему путем добавления команды module load к пользовательскому .cshrc (для пользователей tcsh) или .bashrc (для пользователей bash). Эти файлы находятся на верхнем уровне домашнего каталога пользователя. RCS настоятельно не рекомендует подобную практику. Это затрудняет совместное использование сценариев заданий и кода между пользователями проекта и может привести к конфликтам модулей и неожиданному поведению программного обеспечения, поскольку со временем легко забыть, что модули загружаются автоматически.
Как перенаправить вывод модуля
Этот ответ также касается: Как мне использовать команду grep «module avail»? Короткий ответ: перенаправить стандартную ошибку ( stderr ) на стандартный вывод ( stdout ).Если вы используете оболочку bash, это делается с использованием синтаксиса « 2> & 1 ». Например, чтобы найти python в доступных модулях, вы можете ввести:
scc4% module avail -t 2> & 1 | grep -i питон
В [t] csh команда немного сложнее, потому что нет тривиального способа перенаправить stderr . В следующем примере команда модуля вызывается в отдельном процессе, а затем она передает stderr и stdout на grep :
scc4% (доступный модуль -t) | & grep -i python
Примечание : модуль avail уже имеет встроенные возможности поиска, что позволяет избежать большей части необходимости использовать такие инструменты, как grep.
Как найти список установленных модулей и версию Python с помощью pip?
Вы хотите знать все версии Python, установленные в вашей системе?
Я также записал видео с живым демо. Вы можете посмотреть или продолжить чтение.
Основная сила Python в том, что доступен широкий спектр внешних библиотек. Продолжая писать код на Python, мы устанавливаем множество пакетов. Получить список установленных модулей Python в системе легко.Есть несколько способов сделать это.
Ниже приведены два эффективных способа получить этот список…
1. Использование функции help () (без точки):
Самый простой способ — открыть консоль Python и ввести следующую команду…
справка («модули»)
Это даст вам список установленных модулей в системе. Этот список содержит модули и пакеты, которые предустановлены вместе с вашим Python, а также все остальные, которые вы установили явным образом.
Вот пример выполнения функции справки в моей системе (Python версии 2).
ОГРОМНЫЙ список: O
Вам не нужно устанавливать какие-либо внешние модули, чтобы получить этот список с помощью функции help (). Но эта команда не дает вам никакой другой информации о пакете .
Если вы хотите узнать версию каждого установленного модуля, вы можете использовать программу pip.
2. Использование pip для поиска установленных модулей Python и их версий:
Чтобы найти список пакетов Python, установленных в системе, вы можете использовать программу pip.
Для тех, кто не знает о pip, это лучшая программа, которая используется для установки и управления другими пакетами Python в вашей системе. Для большего понимания вы можете ознакомиться с полным руководством по управлению модулями Python с помощью pip.
Если у вас установлена последняя версия Python, pip поставляется с предварительно установленным Python.
Выполните следующие команды в командной строке (не на консоли Python). Вы получите полный список установленных модулей Python с их версиями.
точка замораживания
или
список пунктов
Вот пример перечисления пакета Python, который вы установили в своей системе с помощью инструмента pip.
В отличие от функции справки, она не выводит список предварительно установленных пакетов Python.
Вы можете увидеть все пакеты Python с указанием их версии.
Примечание: Перед запуском этой команды убедитесь, что в вашей системе установлен пакет. Для Python версий 2.7+ и 3.4+ он поставляется с предварительно установленным Python.
Формат списка вывода обеих команд полностью различается. Предположим, вы используете эту команду в сценариях оболочки.Вы можете выбрать любую из команд, которая вам будет проще проанализировать список выходных пакетов и получить информацию.
Если у вас уже есть код синтаксического анализа для любого вывода двух команд, вы можете использовать эту команду.
Связанное чтение: Почему вы должны изучать сценарии оболочки? (Python против сценариев оболочки)
Чтобы получить более подробностей о каком-либо конкретном модуле , запустите команду.
pip показать getopt
Возвращает имя модуля / пакета, версию, автора, адрес электронной почты автора, лицензию, местонахождение установленного модуля и требования.
Вы можете получить электронную почту автора. Вы можете обратиться к автору по любому конкретному запросу, связанному с пакетом Python.
Если вы используете код Python в коммерческих целях, важно знать лицензию на пакет.
Как проверить, установлен ли модуль Python?
Вы можете использовать команды pip с командой grep для поиска любого конкретного модуля, установленного в вашей системе.
список пунктов | grep getopt
Например, вы также можете перечислить все установленные модули с суффиксом «re» в имени модуля.
список пунктов | grep re
Как подсчитать количество модулей Python, установленных в вашей системе?
Вы можете использовать команду wc (количество слов).
список пунктов | туалет -l
Примечание. Команды grep и wc работают только с системами на базе Linux.
Какая польза от этих команд?
- Эти команды можно использовать для вывода списка всех установленных модулей в вашей системе. Позже вы можете использовать этот список для настройки новой идентичной среды.
- Если вы столкнулись с какой-либо проблемой в установленном пакете Python, выполнение этих команд упростит отладку.
- Зная версию модуля Python, вы можете обновить модуль, если доступна новая версия модуля.
Что дальше?
Отметьте эти 39 самых полезных модулей Python, на которые приходится 95% заданий Python.
В следующей статье я расскажу, как можно написать программу Python, чтобы получить список пакетов Python и сохранить их в списке.
Если вы найдете эти команды полезными для списка установленных модулей Python, поделитесь с друзьями.
Модуль числа в Excel. Как найти модуль числа в Эксель с помощью функции ABS, Корень, Знак, инструкция по нахождению модуля нескольких чисел с фото.
Использование функции ABS
В программе Excel для нахождения модуля числа предусмотрена специальная функция ABS, формула которой в общем виде может выглядеть так:
- ABS(число)
- ABS(адрес_ячейки_с_числом)
Допустим, нам нужно найти модуль числа -27. Для этого в любой свободной ячейке пишем выражение: =ABS(-27).
Нажав клавишу Enter получаем результат в выбранной ячейке.
Некоторые пользователи по привычке пишут в ячейке математическое выражение, а именно, |-27|.
В данном случае после нажатия Enter программа выдаст ошибку.
Вместо того, чтобы вручную прописывать формулы, можно использовать Мастер функций.
- Выбрав ячейку, куда мы планируем добавить функцию и провести расчеты, кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
- В открывшемся окне вставки функций выбираем категорию “Математические”, в предложенном списке кликаем по оператору “ABS” и жмем OK.
- На экране отобразится окно для заполнения аргумента функции – “Число”. Адрес ячейки с числовыми значением, модуль которого нужно посчитать, можно указать вручную, либо просто кликнуть по ней в самой таблице. Курсор при этом должен находиться в поле для ввода значения аргумента. По готовности жмем кнопку OK.
- В ячейке с функцией появится результат вычислений.
- Если нужно посчитать модули по всему столбцу, можно растянуть формулу на другие строки. Для этого наводим указатель мыши на ячейку с результатом, когда появится небольшой черный плюсик, зажав левую кнопку мыши тянем его вниз до последней ячейки столбца (или до той ячейки, для которой нужно посчитать аналогичный результат).
- Все готово, мы получили модули всех значений в исходном столбце.
Источник: http://MicroExcel.ru/funkcziya-modul/
Описание
Возвращает модуль (абсолютную величину) числа. Абсолютная величина числа — это число без знака.
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-abs-3420200f-5628-4e8c-99da-c99d7c87713c
Причины применения функции
В математике модуль числа показывает его абсолютное значение, знак величины не учитывается. С помощью формулы определение записывается так: I-aI = IaI = a. Все значения по модулю являются положительными.
Программа Excel оперирует числами, под которыми часто «скрываются» не абстрактные математические действия, а реальные предметы или бухгалтерские расчеты. Поэтому полученные результаты не могут быть отрицательными.
Например, какие-то товары были проданы сверх плана, другие, наоборот, остались на складе. Тогда реализованные изделия будут иметь положительное значения, а не проданные — отрицательные. Если понадобится сложить все отклонения от плана, то результатом может стать отрицательное значение или ноль. Применение модуля покажет абсолютную сумму отклонений.
Оператор также находит применение при подсчете векторных величин, которые могут иметь отрицательное значение, сравнении двух элементов таблицы, расчете процентов по кредиту.
Источник: http://MyComp.su/obzory/modul-v-eksel-kak-pishetsya.html
В результате вычисления формулыФормула уделить пару секунд=СУММ(СУММЕСЛИ(A2:A8, 0″,»=SUMPRODUCT(ABS(A2:A8)) отличий, но этоВ2180Автор: Максим Тютюшев которое вы выбрали. формул. в приложении MicrosoftМарочка
: =R[-1]C/МАКС(ABS(R[-3]C[-2]:R[-2]C[-2])) не работает отрицательное число, какМодуль числа позволяет определить отобранных отрицательных чисел. по модулю определиласьОписание и сообщить, помогла=SUM(SUMIF(A2:A8, 0″,»
Учитывая, что можно использовать
мало относится к, Excel расширил таблицу:Мой коллега однажды спросилЕсли значение расположено вЗапускается окно Мастера функций.
Excel.: есть, только онадобавляю ABS со сделать так что какую-либо физическую величину,
Если отрицательных чисел (расходных проекция отрезка наРезультат ли она вам,Если мы возьмем первый более эффективную функцию теме данной статьи.
Источник: http://MyComp.su/obzory/modul-v-eksel-kak-pishetsya.html
Расчет разницы между наименьшим отрицательным и положительным числом
Пример 2. Найти разность между наименьшим и наименьшим абсолютным значениями элементов массива.
Исходные данные:
Для расчета используем следующую формулу (формула массива CTRL+SHIFT+Enter):
Функция МИН выполняет поиск наименьшего значения в диапазоне. Для поиска наименьшего неотрицательного числа используется выражение МИН(ABS(B3:B12)).
Полученный результат:

Источник: http://exceltable.com/funkcii-excel/primer-funkcii-modul-abs
Функция «Модуль» в Microsoft Excel
Модуль – это абсолютная положительная величина любого числа. Даже у отрицательного числа модуль будет всегда положительным. Давайте выясним, как рассчитать величину модуля в Microsoft Excel.
Источник: http://vkspy.info/pc/kak-poschitat-modul-chisla-v-eksel-formula-funkcziya
Использование ABS
Поставить модуль числа в Excel можно функцией ABS, аббревиатура образовалась от английского слова Absolute, что означает «абсолютный».
Стандартный вариант
Правильное написание выглядит так: «ABS(X)» или «ABS(адрес_ячейки_с_числом)». Здесь «X» — число, модуль которого нужно найти, «адрес ячейки с числом» — элемент таблицы, в котором будет указано абсолютное значение. Вставить формулу можно двумя способами. Простой вариант:
- Вписать в ячейку или в строку формул значение, для которого нужно найти модуль. Пусть это будет -8. Тогда надпись будет такова: «=ABS(-8)».
- Нажать ввод и получить результат.
Второй вариант:
- Выделить необходимую ячейку и кликнуть по опции «Вставить формулу», обозначенной символом fx.
- В появившемся списке найти надпись «ABS», выделить ее и подтвердить.
- Откроется меню «Аргументы функции». Здесь нужно ввести необходимую цифру в функцию модуля. Можно указать адрес ячейки, в которой находится необходимое значение. Для этого нажать на иконку, находящуюся справа от строки «Число».
- Окно аргументов свернется, в рабочей таблице нужно будет кликнуть по нужному элементу и снова нажать на иконку.
- Опять появится меню с аргументами, где в строке значений будет стоять адрес выбранной ячейки. Подтвердить операцию.
- Функция сработает в указанном месте.
- Можно распространить действие формулы на другие ячейки. Для этого в ячейке с примененной функцией ABS нажать на правый нижний угол мышкой и не отпуская кнопку «потянуть» мышку вниз, выделяя нужные элементы. К ним будет применена функция.
Как правильно рассчитать корень или возвести в степень в Экселе
ABS в формулах
Наряду с простым приведением к модулю, функция может использоваться в связке с формулами и решать комплексные задачи. Например, определить на сколько минимальное отрицательное число меньше минимального положительного можно так:
- Имеется массив, в котором нужно решить поставленную задачу.
- В строку формул нужно вписать следующую композицию: {МИН(ABS(B3:B12))}.Здесь фигурные скобки показывают, что расчеты ведутся с массивом данных. Вводятся такие скобки не с клавиатуры, а нажатием клавиш Ctrl+Shift+Enter в конце написания формулы. Программа в этом случае рассчитывает модуль в каждой из ячеек между B3 и B12. Без применения массивов ABS выдала бы сообщение об ошибке при такой записи.
- Результат применения:
Примеры расчетов
Ниже приведены возможные случаи использования функции модуля ABS, как отдельно, так и в составе формулы.
Задача по математике на определение проекции отрезка на ось абсцисс (X) и ось ординат(Y). По условиям задания отрезок имеет координаты начала A(-17; -14) и конца B(-39;-56). Решение в Excel:
- Ввести в таблицу известные данные.
- Рассчитывается проекция на ось X с помощью ABS.
- Аналогично находится проекция на ось ординат. В строке «Число» нужно указать B5-B3.
- Результат появится в таблице.
Подсчет расходов компании — здесь нужно сложить отрицательные значения по модулю.
Имеется набор финансовых операции компании за отчетный период. Нужно определить сумму трат предприятия. По условию расходы указываются со знаком минус:
- Составить массив в Excel.
- Написать формулу: {=СУММ(ЕСЛИ(В3:В12<0;ABS(В3:В12);0))}В конце нажать Ctrl+Shift+Enter для указания того, что используются массивы данных.
- Программа анализирует данные ячеек B3-B12 и если имеются отрицательные числа, то берется их модуль. После проверки всех элементов, отрицательные значения складываются. Положительные данные не учитываются в расчетах. Итоговый результат имеет следующий вид:
Как посчитать среднее арифметическое в Excel – все доступные способы
Источник: http://MyComp.su/obzory/modul-v-eksel-kak-pishetsya.html
Подключение
Запрос можно использовать для подключения к одному источнику данных, такому как база данных Access, или к нескольким файлам, базам данных, веб-каналам OData или веб-сайтам. Затем вы сможете собрать все эти источники, используя собственные уникальные сочетания, и выявить идеи, которые вы, возможно, не видели иначе.
Выбрав “Получить данные” в разделе “& Преобразовать” на вкладке “Данные” (или “Новый запрос”, если вы не видите кнопку “Получить данные”), вы увидите множество источников данных на выбор. в том числе такие файлы, как книги Excel или текстовые/CSV-файлы, базы данных, такие как Access,SQL Server,Oracleи MySQL,службы Azure, такие как HDInsight или хранилище BLOB-файлов,и другие источники, такие как интернет,списки SharePoint,файлы Hadoop,Facebook,Salesforceи т. д.
Примечание: Узнать о том, какие источники данных доступны в версиях Excel, можно здесь: где найти & Преобразования (Power Query).
При подключении к источнику данных в & “Преобразование” отображается области навигации, с которой можно редактировать данные из источника. Когда вы выбираете “Изменить” в окне “Навигатор”, при &-преобразования запускается редактор запросов,который упрощает и отображает подключения к данным и применяет преобразования. В следующем разделе (Преобразование) вы найдете более подробные сведения о редакторе запросов.
Источник: http://vkspy.info/pc/kak-poschitat-modul-chisla-v-eksel-formula-funkcziya
Альтернативные способы расчета
Если вдруг формула ABS вылетела из головы, и Вы забыли как посчитать модуль в Excel с ее помощью, то рассмотрим несколько способов поиска абсолютной величины числа без использования данной формулы.
С помощью функции ЗНАК
Согласно определению, модуль — это неотрицательное значение исходного числа, поэтому умножая число на 1 или -1 в зависимости от знака числа (то есть положительное умножаем на 1, отрицательное умножаем на -1), мы в итоге получим абсолютную величину:
С помощью функции КОРЕНЬ
Чтобы найти модуль мы также можем воспользоваться свойством вычисления квадратного корня в Excel.
Напомним, что в Excel используется понятие арифметического корня для вычисления корней четных степеней.
Другими словами, корень четной степени в Excel всегда принимает неотрицательное значение, поэтому при извлечении квадратного корня от числа возведенного в квадрат, мы опять в результате получим абсолютную величину:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Источник: http://tutorexcel.ru/funktsii/modul-chisla-v-excel/
Пример
Скопируйте таблицу ниже и вставьте ее в ячейку A1 в Excel. Возможно, для работы формул понадобится выбрать все ячейки с ними и нажать клавишу F2, а затем — клавишу ВВОД. Можно также расширить столбцы для более удобного просмотра листа.
|
Данные |
||
|
-4 |
||
|
Формула |
Описание |
Результат |
|
=ABS(2) |
Абсолютное значение числа 2 |
2 |
|
=ABS(-2) |
Абсолютное значение числа -2 |
2 |
|
=ABS(A2) |
Абсолютное значение числа -4 |
4 |
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-abs-3420200f-5628-4e8c-99da-c99d7c87713c
Что такое модуль
Согласно определению, модуль – это математическое действие, возвращающее абсолютное значение числа, то есть само число без его знака. Несмотря на специфику, использование модуля можно встретить не только при решении математических задач, но также и в экономических моделях, физике и многих других точных науках.
Источник: http://vkspy.info/pc/kak-poschitat-modul-chisla-v-eksel-formula-funkcziya
См. также
Вычитание чисел
Умножение и деление чисел в Excel
Расчет процентов
Нужна дополнительная помощь?
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-abs-3420200f-5628-4e8c-99da-c99d7c87713c
Как найти модуль числа в экселе
Microsoft Office Excel позволяет производить математические операции в таблицах с помощью большого набора встроенных функций. Иногда требуется посчитать сумму абсолютных значений, то есть независимо от того отрицательное или положительное число. Сегодня разберемся, как найти модуль в экселе. Математически это выглядит следующим образом: |x|= x, при x>=0 и |x|= -x, при x
Источник: http://vkspy.info/pc/kak-poschitat-modul-chisla-v-eksel-formula-funkcziya
Функция
Для того чтобы найти модуль числа в Microsoft Excel есть отдельная функция – ABS.
На заметку! Условное обозначение abs используется практически во всех языках программирования, в том числе и Visual Basic (VBA), который используется для написания макросов Excel.
Сейчас рассмотрим, как написать формулу поиска абсолютного значения правильно:
- Создаете столбец чисел, который содержит цифры со знаком плюс и минус. Плюс по умолчанию не отображается.
- В соседней ячейке записываете формулу с функцией ABS.
- Чтобы формула посчитала абсолютное значение остальных ячеек, воспользуйтесь маркером автозаполнения.
Важно! Поставить модуль в формулу в виде вертикальной черты, как в математике, не получится. Такая запись приведет к ошибке, поскольку редактор не распознает подобные символы внутри формулы.
Источник: http://vkspy.info/pc/kak-poschitat-modul-chisla-v-eksel-formula-funkcziya
Excel works!
Excel работает за вас
Источник: http://vkspy.info/pc/kak-poschitat-modul-chisla-v-eksel-formula-funkcziya
Как решать уравнения с модулем: основные правила
30 декабря 2016
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft( x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft( x right) right|=a]
Ну и как такое решать? Напомню: $fleft( x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
или:
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left( 2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
[2x+1=5Rightarrow 2x=4Rightarrow x=2]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 \& 2x+1 lt 0 \end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
[2x+1=-5Rightarrow 2x=-6Rightarrow x=-3]
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft( x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft( x right) right|=aRightarrow fleft( x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; \& 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. \end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; \& 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. \end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft( x right)$ и $gleft( x right)$ :
[left| fleft( x right) right|=gleft( x right)Rightarrow left{ begin{align}& fleft( x right)=pm gleft( x right), \& gleft( x right)ge 0. \end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, \& 2xge 0. \end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2xRightarrow 3x-2x=2Rightarrow x=2; \& 3x-2=-2xRightarrow 5x=2Rightarrow x=frac{2}{5}. \end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5};$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft( x right) right|=gleft( x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left( x-{{x}^{3}} right), \& x-{{x}^{3}}ge 0. \end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; \& 2{{x}^{3}}-3{{x}^{2}}=0; \end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left( 2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 \& 2x-3=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left( x-{{x}^{3}} right); \& {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; \& -3{{x}^{2}}+2x=0; \& xleft( -3x+2 right)=0. \end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 \& -3x+2=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
[x-{{x}^{3}}ge 0]
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; \& x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; \& x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; \end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft( x right) right|=gleft( x right)$ или даже более простому $left| fleft( x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft( x right) right|=left| gleft( x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; \& 2x+3=-left( 2x-7 right)Rightarrow 2x+3=-2x+7. \end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft( x right) right|=left| gleft( x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left( x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
[x-1=pm left( {{x}^{2}}-3x+2 right)]
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; \& {{x}^{2}}-3x+2=-left( x-1 right)Rightarrow {{x}^{2}}-2x+1=0. \end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left( x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; \& left| x-1 right|=left| left( x-1 right)left( x-2 right) right|. \end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; \& left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; \& left| x-1 right|cdot left( 1-left| x-2 right| right)=0. \end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, \& left| x-2 right|=1. \end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; \& 0,004+0,0001=0,0041 gt 0; \& 5+0=5 gt 0. \end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, \& left| {{x}^{2}}+x-2 right|=0. \end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[x-{{x}^{3}}=0Rightarrow xleft( 1-{{x}^{2}} right)=0Rightarrow left[ begin{align}& x=0 \& x=pm 1 \end{align} right.]
[{{x}^{2}}+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin{align}& x=-2 \& x=1 \end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft( x right) right|=gleft( x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
[3x-5 gt 0Rightarrow left| 3x-5 right|=3x-5]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
[3x-5=5-3xRightarrow 6x=10Rightarrow x=frac{5}{3}]
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
[x=frac{5}{3}Rightarrow 3x-5=3cdot frac{5}{3}-5=5-5=0]
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
[3x-5 lt 0Rightarrow left| 3x-5 right|=5-3x]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
[5-3x=5-3x]
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
[3x-5 lt 0Rightarrow 3x lt 5Rightarrow x lt frac{5}{3}]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
[xin left( -infty ;frac{5}{3} right)]
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
[3x-5=0Rightarrow left| 3x-5 right|=0]
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
[0=3x-5Rightarrow 3x=5Rightarrow x=frac{5}{3}]
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Итого окончательный ответ: $xin left( -infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
Смотрите также:
- Простейшие уравнения с модулем
- Уравнение с двумя модулями
- Сложные выражения с дробями. Порядок действий
- Сводный тест по задачам B15 (2 вариант)
- Как решать биквадратное уравнение
- B4: счетчики на электричество
План урока:
Модуль числа
Решение уравнений с модулем
Уравнения с параметрами
Модуль числа
Напомним, что такое модуль числа. Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:
|9| = |– 9| = 9
|674| = |– 674| = 674
|2,536| = |– 2,536| = 2,536
Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:
Именно такое определение обычно и применяется в математике.
Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:
Также модуль возникает при извлечении квадратного корня из четной степени числа:
В частности, если n = 1, получим формулу:
Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:
Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:
В результате получилась «галочка».
Пример. Постройте график ф-ции у = |х2 – 4х + 3|
Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х2 – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:
Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х2 – 4х + 3|, надо перевернуть эту часть графика:
Решение уравнений с модулем
Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число. То есть уравнение имеет вид
|у(х)| = b
где b – какое-то число, а у(х) – произвольная ф-ция.
Если b< 0, то ур-ние корней не имеет, ведь модуль не может быть отрицательным.
Пример. Найдите корни ур-ния
|125x10 + 97x4– 12,56х3 + 52х2 + 1001х – 1234| = – 15
Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.
Ответ: корни отсутствуют.
Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.
Пример. Решите ур-ние
|13х – 52| = 0
Решение.
Ясно, что подмодульное выр-ние равно нулю:
13х – 52 = 0
13х = 52
х = 4
Ответ: 4.
Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число. Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:
|b| = b
|– b| = b
То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.
Пример. Решите ур-ние
|х| = 10
Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.
Ответ: 10; (– 10).
Пример. Решите ур-ние
|10х + 5| = 7
Решение. Исходное ур-ние разбивается на два других ур-ния:
10х + 5 = 7 или 10х + 5 = – 7
10х = 2 или 10х = – 12
х = 0,2 или х = – 1,2
Ответ: 0,2; (– 1,2).
Пример. Найдите корни ур-ния
|x2– 2х – 4| = 4
Решение. Снова заменим исходное равенство на два других:
x2– 2х – 4 = 4 или x2– 2х – 4 = – 4
Имеем два квадратных ур-ния. Решим каждое из них:
x2– 2х – 4 = 4
x2– 2х – 8 = 0
D = b2– 4ас = (– 2)2 – 4•1•(– 
х1 = (2 – 6)/2 = – 2
х2 = (2 + 6)/2 = 4
Нашли корни (– 2) и 4. Решаем второе ур-ние:
x2– 2х – 4 = – 4
x2– 2х = 0
х(х – 2) = 0
х = 0 или х – 2 = 0
х = 0 или х = 2
Получили ещё два корня: 0 и 2.
Ответ: – 2, 4, 0, 2
Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:
|у(х)| = |g(x)|
Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.
Пример. Решите ур-ние
|x2 + 2x– 1| = |х + 1|
Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:
x2 + 2x– 1 = х + 1 или x2 + 2x– 1 = – (х + 1)
х2 + х – 2 = 0 или х2 + 3х = 0
Решим 1-ое ур-ние:
х2 + х – 2 = 0
D = b2– 4ас = 12 – 4•1•(– 2) = 1 + 8 = 9
х1 = (1 – 3)/2 = – 1
х2 = (1 + 3)/2 = 2
Теперь переходим ко 2-омуур-нию:
х2 + 3х = 0
х(х + 3) = 0
х = 0 или х + 3 = 0
х = 0 или х = – 3
Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.
Ответ:(– 1), (– 2), 2, 0.
Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.
Пример. Найдите решение уравнения, содержащего модуль:
|х2 + 3,5х – 20| = 4,5х
Решение. Рассмотрим два отдельных равенства:
х2 + 3,5х – 20 = 4,5х илих2 + 3,5х – 20 = – 4,5х
х2 – х – 20 = 0 или х2 + 8х – 20 = 0
Решим каждое из полученных квадратных ур-ний.
х2 – х – 20 = 0
D = b2– 4ас = 12 – 4•1•(– 20) = 1 + 80 = 81
х1 = (1 – 9)/2 = – 4
х2 = (1 + 9)/2 = 5
х2 + 8х – 20 = 0
D = b2– 4ас = 82 – 4•1•(– 20) = 64 + 80 = 144
х3 = (– 8 – 12)/2 = – 10
х4 = (– 8 + 12)/2 = 2
Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:
4,5х ≥ 0
Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.
Ответ: 2 и 5
Мы рассмотрели три случая, когда ур-ние имеет вид:
- у(х) = b (b– это некоторая константа)
- |у(х)| = |g(x)|
- |у(х)| = g(x)
Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.
Пример. Найдите корни ур-ния
|x + 1| + |x– 4| = 6
Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:
Если отметить обе точки на прямой, то они образуют на ней 3 интервала:
Исследуем ур-ние на каждом из полученных промежутков.
Так как при х <– 1 оба подмодульные выр-ния отрицательны, то можно записать, что
|x + 1| = – (х + 1) = – х – 1
|x– 4| = – (х – 4) = – х + 4
Тогда ур-ние примет вид
|x + 1| + |x– 4| = 6
– х – 1 – х + 4 = 6
–2х = 3
х = – 1,5
Это значение удовлетворяет условию х <– 1, поэтому корень верный.
Далее изучим случай, когда х∊[– 1; 4). Здесь отрицательно только выражение x– 4, поэтому модули заменяются так:
|x + 1| = х + 1
|x– 4| = – (х – 4) = – х + 4
Ур-ние примет вид:
|x + 1| + |x– 4| = 6
x + 1 – x+ 4 = 6
5 = 6
Получили неверное тождество. Получается, что на промежутке [– 1; 4) корней нет.
При х ≥4 выр-ния х – 4 и х + 1 положительны, поэтому
|x + 1| = х + 1
|x– 4| = х – 4
Исходное ур-ние будет выглядеть так
|x + 1| + |x– 4| = 6
х + 1 + х – 4 = 6
2х = 9
х = 4,5
Найденный корень удовлетворяет условию х ≥4, поэтому он также должен быть включен в ответ.
Уравнения с параметрами
Изучим ур-ния:
5х = 10
5х = 15
5х = 20
Для решения каждого из них надо число справа поделить на 5 (множитель перед х). В итоге получаем значения х, равные 2, 3 и 4.
Теперь обозначим число в правой части буквой, например, как v. Тогда все эти ур-ния будут выглядеть одинаково:
5х = v
Решением таких ур-ний будет дробь v/5.
Надо понимать разный смысл, который мы вкладываем при этом в буквы х и v. Через х мы обозначили переменную, то есть ту величину, значение которой необходимо найти. Под буквой v подразумевалась заранее известная величина, то есть константа, которая известна заранее в каждом конкретном ур-нии. Такую величину называют параметром, а ур-ние 5х = v называют уравнением с параметром.
Изучая уравнение с параметром, мы рассматриваем не одно конкретное ур-ние, а сразу целую группу, или семейство ур-ний. Например, все ур-ния первой степени можно описать в виде
ах + b= 0
где х – это переменная величина, а числа а, b– это параметры. Для описания квадратного ур-ния в общем виде необходимы уже три параметра (а, b и с):
ах2 + bx + c = 0
Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.
Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.
Пример. Решите ур-ние
х2 – 2ах = 0
и найдите его корни при значении параметра а, равном 3.
Решение. Вынесем множитель х за скобки:
х2 – 2ах = 0
х(х – 2а) = 0
х = 0 или х – 2а = 0
х = 0 или х = 2а
Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:
при а = 3х = 2•3 = 6
Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.
Пример. Решите ур-ние
р2х – 3рх = р2 – 9
Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:
рх(р – 3) = (р – 3)(р + 3)
Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.
Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во
0•х•(0 – 3) = (0 – 3) (3 – 0)
0 = – 9
Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.
Если р – 3 = 0, то есть р = 3, получится следующее
3•х•0 = 0•(3 + 3)
0 = 0
Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.
Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим
В этом случае ур-ние имеет единственный корень.
Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.
Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.
Пример. Сколько корней имеет ур-ние
|х2 – 6х + 5| = b
при различных значениях параметра b.
Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х2 – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:
х2 – 6х + 5 = 0
D = b2– 4ас = (– 6)2 – 4•1•5 = 36 + 20 = 16
х1 = (6 – 4)/2 = 1
х2 = (6 + 4)/2 = 5
Итак, нули ф-ции – это точки 1 и 5. Найдем координату х0 вершины параболы по формуле:
х0 = –b/2a = 6/2 = 3
Подставив х0 в квадратичную ф-цию найдем координату у0 вершины параболы:
32 – 6•3 + 5 = 9 – 18 + 5 = – 4
Теперь построим квадратичную ф-цию:
Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:
Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:
При b< 0 прямая пролегает ниже графика. Общих точек у графиков нет, а потому ур-ние корней не имеет.
При b = 0 прямая у = 0 касается графика в 2 точках: (1; 0) и (5; 0). Получаем 2 корня.
Если 0 <b< 4, то прямая пересекает график в 4 точках.
При b = 4 прямая у = 4 касается перевернутой вершины параболы, а также пересекает ветви ещё в 2 точках. Итого 3 корня.
Наконец, при b>4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.
Ответ: нет корней при b< 0; 2 корня при b = 0 и b> 4; 3 корня при b = 4; 4 корня при 0 <b< 4.
Пример. При каком а ур-ние
х4 – (а + 2)х2 + 3а – 3 = 0
имеет ровно 4 корня?
Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х2:
у2 – (а + 2)у + 3а – 3 = 0 (1)
Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у1 и у2. Тогда, проводя обратную замену х2 = у1 и х2 = у2, мы получим два разных квадратных ур-ния, корни которых будут равны
Если же хоть один из двух корней, например, у1, окажется равным нулю, то величины
Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у1 будет отрицательным числом, то ур-ние
х2 = у1
вовсе не будет иметь решений, и тогда останется не более 2 корней.
Итак, решим ур-ние (1):
у2 – (а + 2)у + 3а – 3 = 0
D = b2– 4ас = (– (а + 2))2 – 4•1•(3а – 3) = (а + 2)2 – 12 а + 12 =
= а2 + 4а + 4 – 12а + 12 = а2 – 8а + 16 = а2 – 2•4•а + 42 = (а – 4)2
Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4)2 положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.
Извлечем корень из дискриминанта:
Корни ур-ния (1) можно вычислить по формулам:
И у1, и у2 должны быть положительными величинами, однако у1 меньше, чем у2 (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:
Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство
|а – 4| = а – 4
Тогда имеем
а + 2 – (а – 4) > 0
6> 0
Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.
Если а < 4, то справедливо соотношение
|а – 4| = – (а – 4)
Тогда получится следующее:
а + 2 – |а – 4|> 0
а + 2 – (– (а – 4)) > 0
а + 2 + а – 4 > 0
2а > 2
а > 1
Итак, при условии, что а< 4, должно выполняться нер-во а > 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение
а > 4
можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).
Ответ: а∊(1; 4)∪(4; + ∞).
Пример. При каких параметрах а у ур-ния
х2 – 2(а + 1)х + а2 + 2а – 3 = 0
существует два корня, которые принадлежат интервалу (– 5; 5)?
Решение. Данное ур-ние является квадратным. Найдем его дискриминант:
D = b2– 4ас = (– 2(а + 1))2 – 4•1•( а2 + 2а – 3) = 4(а2 + 2а + 1) – 4(а2 + 2а – 3) =
= 4(а2 + 2а + 1 – а2– 2а + 3) = 4•4 = 16
Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам
Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х1) был больше – 5, больший (это х2) – меньше – 5:
Значит, должны выполняться два нер-ва
х1>– 5и х2<5
а – 1 >– 5 и а + 3 < 5
а >– 4 и а < 2
Эти два нер-ва выполняются, если а∊(– 4; 2)
Ответ: (– 4; 2)
Модулем комплексного числа z=x+iyz = x+iy называется вещественное число, равное
∣z∣=x2+y2.|z| = sqrt{x^2+y^2}.
Модуль всегда определен (другими словами, модуль есть у любого комплексного числа): в самом деле, какими бы ни были xx и yy, сумма квадратов x2+y2x^2+y^2 есть число неотрицательное, а значит, из него можно извлечь квадратный корень, и он тоже будет неотрицательным числом. Модуль равен нулю в единственном случае: если z=0z=0, то есть x=y=0x=y=0. Если же хотя бы одна из координат x,yx, y отлична от нуля, ее квадрат будет строго положительным, и, следовательно, значение выражения x2+y2sqrt{x^2+y^2} также будет строго положительным. Итак, модуль любого ненулевого числа есть строго положительное число.
Мы знаем, что любое вещественное число можно представить как комплексное число с нулевой мнимой частью:
x=x+0⋅i.x = x + 0 cdot i.
Для такого числа формула модуля дает следующий результат:
∣z∣=x2+02=x2=∣x∣.|z| = sqrt{x^2+0^2} = sqrt{x^2} = |x|.
Таким образом, для вещественных чисел новое (комплексное) определение модуля совпадает со старым. Так и должно быть, если мы расширяем известное понятие.
Говорят, что понятие модуля комплексного числа обобщает понятие модуля вещественного числа.
Как найти модуль комплексного числа
Модуль числа выражает расстояние от этого числа до нуля. В самом деле, на плоскости расстояние между точками с координатами (x,y)(x,y) и (x1,y1)(x_1,y_1) вычисляется по формуле
d=(x−x1)2+(y−y1)2.d = sqrt{(x-x_1)^2+(y-y_1)^2}.
Если в этой формуле положить x1=y1=0x_1=y_1=0, то есть в качестве второй точки взять начало координат, то мы получим
d=x2+y2.d = sqrt{x^2+y^2}.
Эта формула выражает расстояние до начала координат от точки (x,y)(x,y), и это расстояние в точности равно модулю комплексного числа x+yi.x+yi.
Для примера на следующем рисунке изображено комплексное число 4+3i,4+3i, модуль которого равен 42+32=25=5sqrt{4^2+3^2} = sqrt{25} = 5. Отрезок длины 55, соединяющий начало координат с точкой (4,3)(4,3), служит гипотенузой прямоугольного треугольника с катетами 44 и 33.
Все комплексные числа, модуль которых равен определенному положительному числу rr, образуют окружность радиуса rr с центром в нуле. На следующем рисунке изображена окружность радиуса 11, на которой лежат все комплексные числа единичного модуля (среди них числа 1,1, −1,-1, ii и −i-i).
Пример решения задачи
Найти модули комплексных чисел 6+8i, 8−6i, −15, 4i,32+12i.6+8i, 8-6i, -15, 4i, frac{sqrt{3}}{2}+frac{1}{2}i.
Решение
∣6+8i∣=62+82=100=10.|6+8i| = sqrt{6^2+8^2} = sqrt{100} = 10.
∣8−6i∣=82+(−6)2=100=10.|8-6i| = sqrt{8^2+(-6)^2} = sqrt{100} = 10.
∣−15∣=∣−15+0⋅i∣=(−15)2+02=152=15.|-15| = |-15+0 cdot i| = sqrt{(-15)^2+0^2} = sqrt{15^2} = 15.
∣4i∣=∣0+4i∣=02+42=42=4.|4i| = |0+4i| = sqrt{0^2+4^2} = sqrt{4^2} = 4.
∣32+12i∣=(32)2+(12)2=34+14=1=1.|frac{sqrt{3}}{2}+frac{1}{2}i| = sqrt{left(frac{sqrt{3}}{2}right)^2 + left(frac{1}{2}right)^2} = sqrt{frac{3}{4} + frac{1}{4}} = sqrt{1} = 1.




 Курсор при этом должен находиться в поле для ввода значения аргумента. По готовности жмем кнопку OK.
Курсор при этом должен находиться в поле для ввода значения аргумента. По готовности жмем кнопку OK.

 Предположим, это -12.
Предположим, это -12. Соответственно, можно считать, что способ нахождения математического модуля выполнен верно.
Соответственно, можно считать, что способ нахождения математического модуля выполнен верно.
 __файл__
__файл__