Как найти умножение комплексных чисел - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Умножение комплексных чисел в алгебраической форме
Умножение комплексных чисел в геометрической форме

Умножение комплексных чисел в алгебраической форме

Определение

Произведением двух комплексных чисел $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$$z_{2}=a_{2}+b_{2} i$ называется
комплексное число
$z$, равное

$z=z_{1} cdot z_{2}=left(a_{1} a_{2}-b_{1} b_{2}right)+left(a_{1} b_{2}+b_{1} a_{2}right) i$

На практике чаще всего комплексные числа перемножают как алгебраические двучлены
$left(a_{1}+b_{1} iright)left(a_{2}+b_{2} iright)$, просто раскрыв скобки, в
полученном результате надо учесть, что $i^{2}=-1$ .

Пример

Задание. Найти произведение комплексных чисел
$z_{1}=2+3 i$ и
$z_{2}=-1+i$ .

Решение. Перемножим заданные комплексные числа как два двучлена, то есть

$z_{1} cdot z_{2}=(2+3 i)(-1+i)=2 cdot(-1)+2 cdot i+3 i cdot(-1)+3 i cdot i=$

$=-2+2 i-3 i+3 i^{2}=-2-i+3 cdot(-1)=-5-i$

Ответ. $z_{1} cdot z_{2}=-5-i$

Умножение комплексных чисел в геометрической форме

Если комплексные числа $z_{1}$ и
$z_{2}$ заданы в
геометрической форме:
$z_{1}=left|z_{1}right|left(cos phi_{1}+i sin phi_{1}right)$,
$z_{2}=left|z_{2}right|left(cos phi_{2}+i sin phi_{2}right)$, то произведением этих чисел есть число

$z_{1} z_{2}=left|z_{1}right| cdotleft|z_{2}right|left[cos left(phi_{1}+phi_{2}right)+i sin left(phi_{1}+phi_{2}right)right]$

То есть модуль произведения двух комплексных чисел в тригонометрической форме равен произведению
модулей сомножителей, а аргумент равен сумме аргументов сомножителей.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти произведение чисел
$z_{1}=3 cdotleft(cos 10^{circ}+i sin 10^{circ}right)$,
$z_{2}=2 cdotleft(cos 50^{circ}+i sin 50^{circ}right)$ .

Решение. Модуль произведения равен
$|z|=3 cdot 2=6$, а аргумент
$phi=10^{circ}+50^{circ}=60^{circ}$, а тогда искомое число в
тригонометрической форме имеет вид:

$z=|z|(cos phi+i sin phi)=6 cdotleft(cos 60^{circ}+i sin 60^{circ}right)$

Запишем результат в
алгебраической форме, для этого вычислим значения соответствующих тригонометрических
функций, будем в результате иметь:

$z=6 cdotleft(frac{1}{2}+i cdot frac{sqrt{3}}{2}right)=3+3 sqrt{3} i$

Ответ. $z=6 cdotleft(cos 60^{circ}+i sin 60^{circ}right)=3+3 sqrt{3} i$

Читать дальше: деление комплексных чисел.

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно найти произведение двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.

Умножение в алгебраической форме
Произведение в тригонометрической форме

Умножение в алгебраической форме

Произведением двух комплексных чисел x = a₁ + b₁i и y = a₂ + b₂i также является комплексное число z:

z = x ⋅ y = (a₁a₂ – b₁b₂) + (a₁b₂ + b₁a₂) ⋅ i

Формула получается путем перемножения двучленов (a₁ + b₁i)(a₂ + b₂i). При этом не забываем, что i² = -1.

Пример 1
Найдем произведением комплексных чисел: x = 3 + 7i и y = 2 – i.

Решение:
x ⋅ y = (3 + 7i)(2 – i) = 3 ⋅ 2 – 3 ⋅ i + 7i ⋅ 2 – 7i ⋅ i = 6 – 3i + 14i – 7i² = 6 + 11i – 7 ⋅ (-1) = 13 + 11i.

Произведение в тригонометрической форме

Комплексные числа могут быть заданы в тригонометрической форме, например x = |x| ⋅ (cos φ₁ + i ⋅ sin φ₁) и y = |y| ⋅ (cos φ₂ + i ⋅ sin φ₂).

В этом случае формула произведения выглядит следующим образом:

x ⋅ y = |x| ⋅ |y| ⋅ [cos(φ₁ + φ₂) + i ⋅ sin(φ₁ + φ₂)]

Пример 2
Выполним умножение двух комплексных чисел: x = 2 ⋅ (cos 15° + i ⋅ sin 15°) и y = 5 ⋅ (cos 30° + i ⋅ sin 30°).

Решение:
|x| ⋅ |y| = 2 ⋅ 5 = 10
φ₁ + φ₂ = 15° + 30° = 45°
x ⋅ y = 10 ⋅ (cos 45° + i ⋅ sin 45°)

Источник

В этой статье рассмотрим правила умножения комплексных чисел. Если у вас возникают вопросы о том, что же такое комплексные числа, то обратитесь к этой статье. Правила сложения и вычитания комплексных чисел рассмотрены здесь.

Чтобы умножить комплексные числа необходимо:

Действительную часть первого комплексного числа умножить на действительную часть второго комплексного числа.

Мнимую часть первого комплексного числа умножить на
мнимую часть второго комплексного числа.

Или в виде формулы умножения комплексных чисел:

(a + b i ) (c + d i ) = a c + a d i + b c i + b d i ²

Но поскольку i ² = −1 , то получаем:

(a + b i ) (c + d i ) = ac + ad i + b c i — b d

Рассмотрим пример умножения комплексных чисел:

(3 + 2 i ) (1 + 7 i)= 3 · 1 + 3 · 7 i + 2 i · 1 + 2 i · 7 i = = 3 + 21 i + 2 i + 14 i ² = 3 + 21 i + 2 i — 14 = −11 + 23 i

Еще пример:

(1 + i ) ² = (1 + i ) (1 + i )= 1 · 1 + 1 · i + 1 · i + i ² = 1 + 2 i — 1 = 0 + 2 i = 2 i

Но можно умножать быстрее, используя формулу:

(a + b i ) (c + d i ) = (ac − bd) + (ad + bc) i

Пример применения формулы умножения комплексных чисел:

(3 + 2 i ) (1 + 7 i ) = (3 · 1 — 2 · 7) + (3 · 7 + 2 · 1) i = −11 + 23 i

Давайте попробуем i ²

Мы можем написать i с действительной и мнимой частью как 0 + i

i ² = (0 + i) ²= (0 + i) (0 + i) = (0 · 0 — 1 · 1) + (0 · 1 + 1 · 0) i = −1 + 0 i = −1

И это хорошо согласуется с определением, что i ² = -1

Так что все прекрасно работает!

Источник

Александр Мельник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Умножение на число и умножение заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.

Определение 1

Произведением заданного комплексного числа $z=a+bcdot i$ на действительное число $k$ является комплексное число, которое определяется равенством

[kcdot z=kcdot (a+bcdot i)=kcdot a+kcdot bcdot i.]

Пример 1

Выполнить умножение комплексных чисел на число $k=sqrt{3} $:

1) $z_{1} =sqrt{3} +sqrt{3} cdot i$; 2) $z_{2} =5-4cdot i$; 3) $z_{3} =sqrt{3} cdot i$.

Решение:

Для умножения комплексных чисел на число воспользуемся определением и получим:

1) $kcdot z_{1} =sqrt{3} cdot z_{1} =sqrt{3} cdot left(sqrt{3} +sqrt{3} cdot iright)=sqrt{3} cdot sqrt{3} +sqrt{3} cdot sqrt{3} cdot i=3+3cdot i$;

2) $kcdot z_{2} =sqrt{3} cdot z_{2} =sqrt{3} cdot (5-4cdot i)=sqrt{3} cdot 5-sqrt{3} cdot 4cdot i=5sqrt{3} -4sqrt{3} cdot i$;

3) $kcdot z_{3} =sqrt{3} cdot z_{3} =sqrt{3} cdot (0+sqrt{3} cdot i)=sqrt{3} cdot sqrt{3} cdot i=3i$.

Примечание 1

При умножении заданного комплексного числа $z=a+bcdot i$ на число $k, , (|k|>1)$ модуль этого числа увеличивается в $|k|$ раз:

[|kcdot z|=|k|cdot sqrt{a^{2} +b^{2} } .]

Примечание 2

При умножении заданного комплексного числа $z=a+bcdot i$ на число $k, , (|k|

[|kcdot z|=frac{sqrt{a^{2} +b^{2} } }{left|frac{1}{k} right|} .]

Примечание 3

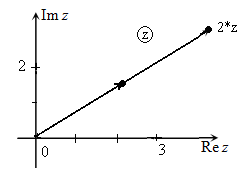
Графическая интерпретация операции умножения заданного комплексного числа $z=a+bcdot i$ на число $k, , (|k|>1)$: длина радиус-вектора, изображающего исходное комплексное число, увеличивается в $|k|$ раз (радиус-вектор становится длиннее в $|k|$ раз).

Примечание 4

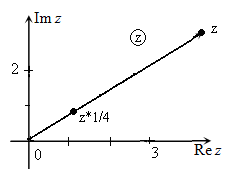
Графическая интерпретация операции умножения заданного комплексного числа $z=a+bcdot i$ на число $k, , (|k|

«Умножение комплексных чисел» 👇

Иллюстрация примера умножения заданного комплексного числа $z=a+bcdot i$ на число $k_{1} =2,, , k_{2} =frac{1}{4} $ с использованием комплексной плоскости приведена на рис.1-2.

Рис. 1

Рис. 2

Определение 2

Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.

Пример 2

Вычислить $i^{k} $ для $k=3..7$.

Решение:

[i^{2} =-1]

[i^{3} =i^{2} cdot i=-1cdot i=-i]

[i^{4} =i^{2} cdot i^{2} =-1cdot (-1)=1]

[i^{5} =i^{2} cdot i^{3} =-1cdot (-i)=i]

[i^{6} =(i^{2} )^{3} =(-1)^{3} =-1]

[i^{7} =(i^{2} )^{3} cdot i=(-1)^{3} cdot i=-1cdot i=-i]

Пример 3

Выполнить умножение комплексных чисел:

1) $z_{1} =1+3i$ и $z_{2} =3-5i$; 2) $z_{1} =sqrt{3} +2i$ и $z_{2} =sqrt{5} cdot i$.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) $z_{1} cdot z_{2} =(1+3i)cdot (3-5i)=1cdot 3+3cdot 3i+1cdot (-5i)+3icdot (-5i)=3+9i-5i-15i^{2} =3+4i+15=18+4i$

2)[begin{array}{l} {z_{1} cdot z_{2} =(sqrt{3} +2i)cdot (0+sqrt{5} cdot i)=sqrt{3} cdot 0+0cdot 2i+sqrt{3} cdot sqrt{5} cdot i+2icdot sqrt{5} cdot i=0+0+sqrt{15} cdot i+2sqrt{5} cdot i^{2} =sqrt{15} cdot i-2sqrt{5} =-2sqrt{5} +sqrt{15} cdot i} end{array}]

Замечание 1

Произведение комплексно-сопряженных чисел $z=a+bcdot i$ и $overline{z}=a-bcdot i$ определяется равенством

[zcdot overline{z}=a^{2} +b^{2} ]

или

[zcdot overline{z}=|z|^{2} =|overline{z}|^{2} .]

Другими словами, произведение комплексно-сопряженных чисел есть квадрат модуля каждого из них.

Пример 4

Выполнить умножение комплексно-сопряженных чисел, используя замечание 1 и определение:

1) $z=1+3i$ и $overline{z}=1-3i$; 2) $z=sqrt{3} +2i$ и $overline{z}=sqrt{3} -2i$.

Решение:

Для умножения комплексных чисел воспользуемся замечанием 1 и получим:

1) $zcdot overline{z}=(1+3i)cdot (1-3i)=1^{2} +3^{2} =1+9=10$

2) [zcdot overline{z}=(sqrt{3} +2i)cdot (sqrt{3} -2i)=(sqrt{3} )^{2} +2^{2} =3+4=7]

Для умножения комплексных чисел воспользуемся определением и получим:

1) $zcdot overline{z}=(1+3i)cdot (1-3i)=1cdot 1+1cdot 3i+1cdot (-3i)+3icdot (-3i)=1+3i-3i-9i^{2} =1+9=10$

2) $begin{array}{l} {zcdot overline{z}=(sqrt{3} +2i)cdot (sqrt{3} -2i)=sqrt{3} cdot sqrt{3} +sqrt{3} cdot 2i-sqrt{3} cdot 2cdot i+2icdot (-2)cdot i=3+2sqrt{3} cdot i-2sqrt{3} cdot i-2^{2} cdot i^{2} =3+4=7} end{array}$

Результаты выполнения операции умножения комплексных чисел совпадают.

Определение 3

Произведением двух заданных комплексных чисел в тригонометрической форме $z_{1} =r_{1} cdot (cos varphi _{1} +isin varphi _{1} )$ и $z_{2} =r_{2} cdot (cos varphi _{2} +isin varphi _{2} )$ является комплексное число, которое определяется равенством

[z_{1} cdot z_{2} =r_{1} cdot r_{2} cdot [cos (varphi _{1} +varphi _{2} )+isin (varphi _{1} +varphi _{2} )].]

Пример 5

Выполнить умножение комплексных чисел:

1) $z_{1} =sqrt{3} cdot (cos frac{pi }{4} +icdot sin frac{pi }{4} )$ и $z_{2} =2cdot (cos frac{2pi }{3} +icdot sin frac{2pi }{3} )$;

2) $z_{1} =4cdot (cos pi +icdot sin pi )$ и $z_{2} =5cdot (cos frac{pi }{2} +icdot sin frac{pi }{2} )$.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) $begin{array}{l} {z_{1} cdot z_{2} =left(sqrt{3} cdot (cos frac{pi }{4} +icdot sin frac{pi }{4} )right)cdot left(2cdot (cos frac{2pi }{3} +icdot sin frac{2pi }{3} )right)=2cdot sqrt{3} cdot [cos (frac{pi }{4} +frac{2pi }{3} )+icdot sin (frac{pi }{4} +frac{2pi }{3} )]=2sqrt{3} cdot (cos frac{11pi }{12} +icdot sin frac{11pi }{12} )} end{array}$

2) [begin{array}{l} {z_{1} cdot z_{2} =left(4cdot (cos pi +icdot sin pi )right)cdot left(5cdot (cos frac{pi }{2} +icdot sin frac{pi }{2} )right)=4cdot 5cdot [cos (pi +frac{pi }{2} )+icdot sin (pi +frac{pi }{2} )]=20cdot (cos frac{3pi }{2} +icdot sin frac{3pi }{2} )} end{array}]

Определение 4

Произведением двух заданных комплексных чисел в показательной форме $z_{1} =r_{1} cdot e^{ivarphi _{1} } $ и $z_{2} =r_{2} cdot e^{ivarphi _{2} } $ является комплексное число, которое определяется равенством

[z_{1} cdot z_{2} =r_{1} cdot e^{ivarphi _{1} } cdot r_{2} cdot e^{ivarphi _{2} } =r_{1} cdot r_{2} cdot e^{i(varphi _{1} +varphi _{2} )} .]

Пример 6

Выполнить умножение комплексных чисел:

1) $z_{1} =sqrt{3} cdot e^{icdot frac{pi }{4} } $ и $z_{2} =2cdot e^{icdot frac{pi }{3} } $; 2) $z_{1} =sqrt{5} cdot e^{icdot frac{2pi }{3} } $ и $z_{2} =2cdot e^{icdot frac{pi }{2} } $.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) [z_{1} cdot z_{2} =left(sqrt{3} cdot e^{icdot frac{pi }{4} } right)cdot left(2cdot e^{icdot frac{pi }{3} } right)=2cdot sqrt{3} cdot e^{icdot (frac{pi }{4} +frac{pi }{3} )} =2sqrt{3} cdot e^{icdot frac{7pi }{12} } ]

2) [z_{1} cdot z_{2} =left(sqrt{5} cdot e^{icdot frac{2pi }{3} } right)cdot left(2cdot e^{icdot frac{pi }{2} } right)=2cdot sqrt{5} cdot e^{icdot (frac{2pi }{3} +frac{pi }{2} )} =2sqrt{3} cdot e^{icdot frac{7pi }{6} } ]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Умножение комплексных чисел

Настал
момент познакомить вас со знаменитым
равенством:

Пример
3

Найти
произведение комплексных чисел
,

Очевидно,
что произведение следует записать
так:

Что
напрашивается? Напрашивается раскрыть
скобки по правилу умножения многочленов.
Так и нужно сделать! Все алгебраические
действия вам знакомы, главное, помнить,
что
и
быть внимательным.

Повторим,
omg, школьное правило умножения многочленов:
Чтобы умножить многочлен на многочлен
нужно каждый член одного многочлена
умножить на каждый член другого
многочлена.

Я
распишу подробно:

Надеюсь,
всем было понятно, что

Внимание,
и еще раз внимание, чаще всего ошибку
допускают в знаках.

Как
и сумма, произведение комплексных чисел
перестановочно, то есть справедливо
равенство:
.

В
учебной литературе и на просторах Сети
легко найти специальную формулу для
вычисления произведения комплексных
чисел. Если хотите, пользуйтесь, но мне
кажется, что подход с умножением
многочленов универсальнее и понятнее.
Формулу приводить не буду, считаю, что
в данном случае – это забивание головы
опилками.

Деление комплексных чисел

Пример
4

Даны
комплексные числа
,
.
Найти частное
.

Составим
частное:

Деление
чисел осуществляется методом
умножения знаменателя и числителя на
сопряженное знаменателю выражение.

Вспоминаем
бородатую формулу
и
смотрим на наш знаменатель:
.
В знаменателе уже есть
,
поэтому сопряженным выражением в данном
случае является
,
то есть

Согласно
правилу, знаменатель нужно умножить
на
,
и, чтобы ничего не изменилось, домножить
числитель на то же самое число
:

Далее
в числителе нужно раскрыть скобки
(перемножить два числа по правилу,
рассмотренному в предыдущем пункте). А
в знаменателе воспользоваться
формулой
(помним,
что
и
не путаемся в знаках!!!).

Распишу
подробно:

Пример
я подобрал «хороший», если взять два
числа «от балды», то в результате деления
почти всегда получатся дроби, что-нибудь
вроде
.

В
ряде случаев перед делением дробь
целесообразно упростить, например,
рассмотрим частное чисел:
.
Перед делением избавляемся от лишних
минусов: в числителе и в знаменателе
выносим минусы за скобки и сокращаем
эти минусы:
.
Для любителей порешать приведу правильный
ответ:

Редко,
но встречается такое задание:

Пример
5

Дано
комплексное число
.
Записать данное число в алгебраической
форме (т.е. в форме
).

Приём
тот же самый – умножаем знаменатель и
числитель на сопряженное знаменателю
выражение. Снова смотрим на формулу
.
В знаменателе уже есть
,
поэтому знаменатель и числитель нужно
домножить на сопряженное выражение
,
то есть на
:

Пример
6

Даны
два комплексных числа
,
.
Найти их сумму, разность, произведение
и частное.

Это
пример для самостоятельного решения.
Полное решение и ответ в конце урока.

Иногда
для решения предлагается навороченный
пример, где нужно выполнить много
действий с комплексными числами. Никакой
паники: будьте
внимательны,
соблюдайте правила алгебры, обычный
алгебраический порядок действий, и
помните, что

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник