Как найти умножение вектора на число

Умножение вектора на число

Навигация по странице:

• Геометрическая интерпретация умножения вектора на число.
• Алгебраическая интерпретация умножения вектора на число.
• Формулы умножения вектора на число
  • для плоских задач
  • для пространственных задач
  • для n -мерного вектора
• Свойства вектора умноженного на число
• Примеры задач на умножение вектора и числа
  • плоская задача
  • пространственных задача

Геометрическая интерпретация.

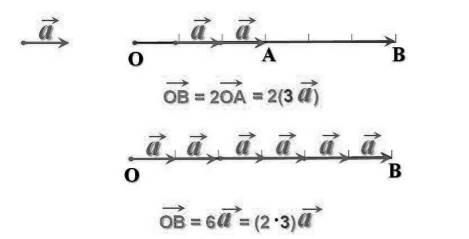
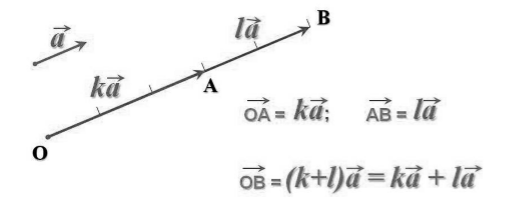
Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; … ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a₁; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2. Найти произведение вектора a = {1; 2; -5} на -2.

Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

В данной публикации мы рассмотрим, каким образом вектор можно умножить на число (геометрическая интерпретация и алгебраическая формула). Также перечислим свойства этого действия и разберем примеры задач.

• Геометрическая интерпретация произведения

• Формула умножения вектора на число

• Свойства произведения вектора и числа

• Примеры задач

Геометрическая интерпретация произведения

Если вектор a умножить на число m, то получится вектор b, при этом:

• b || a
• |b| = |m| · |a|
• b ↑↑ a, если m > 0, b ↑↓ a, если m < 0

Таким образом, произведением ненулевого вектора на число является вектор:

• коллинеарный исходному;
• сонаправленный (если число больше нуля) или имеющий противоположное направление (если число меньше нуля);
• Длина равняется длине иходного вектора, умноженной на модуль числа.

Формула умножения вектора на число

Произведение ненулевого вектора на число – это вектор, координаты которого равняются соответствующим координатам исходного вектора, умноженным на заданное число.

Для плоских задач	a · m = {ax · m; ay · m}
Для трехмерных задач	a · m = {ax · m; ay · m; az · m}
Для n-мерных векторов	a · m = {a1 · m; a2 · m; … an · m}

Свойства произведения вектора и числа

Для любых произвольных векторов и чисел:

• (m ± n) · a = m · a ± n · a
• m · (a ± b) = m · a ± m · b
• m · (n · a) = (m · n) · a = n · (m · a)
• 1 · a = a
• 0 · a = 0

Примеры задач

Задание 1
Найдем произведение вектора a = {5; 11} и числа 4.

Решение:
4 · a = {4 · 5; 4 · 11} = {20; 44}

Задание 2
Умножим вектор b = {2; -4; 7} на число -6.

Решение:
-6 · b = {(-6) · 2; (-6) · (-4); (-6) · 7} = {-12; 24; -42}.

Умножение вектора на число

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Откладывание вектора от данной точки

Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Определение 1

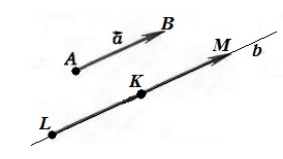
Если точка $A$ начала какого-либо вектора $overrightarrow{a}$, то говорят, что вектор $overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $overrightarrow{a}$ отложенный от точки $A$

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $overrightarrow{a}$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

1. Вектор $overrightarrow{a}$ — нулевой.

   В этом случае, очевидно, что искомый вектор — вектор $overrightarrow{KK}$.

2. Вектор $overrightarrow{a}$ — ненулевой.

   Обозначим точкой $A$ начало вектора $overrightarrow{a}$, а точкой $B$ — конец вектора $overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $overrightarrow{a}$. Отложим на этой прямой отрезки $left|KLright|=|AB|$ и $left|KMright|=|AB|$. Рассмотрим векторы $overrightarrow{KL}$ и $overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $overrightarrow{a}$ (рис. 2)

   

   Рисунок 2. Иллюстрация теоремы 1

   Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

   Теорема доказана.

Умножение вектора на число

Пусть нам дан вектор $overrightarrow{a }$ и действительное число $k$.

Определение 2

Произведением вектора $overrightarrow{a }$ на действительное число $k$ называется вектор $overrightarrow{b }$ удовлетворяющий следующим условиям:

1. Длина вектора $overrightarrow{b }$ равна $left|overrightarrow{b }right|=left|kright||overrightarrow{a }|$;

2. Векторы $overrightarrow{a }$ и $overrightarrow{b }$ сонаправлены, при $kge 0$ и противоположно направлены, если $k

Обозначение: $ overrightarrow{b }=koverrightarrow{a }$.

Замечание 1

Отметим, что в результате произведения вектора на число всегда получается векторная величина.

Свойства произведения вектора на число

1. Произведение любого вектора с числом ноль равняется нулевому вектору.

   Доказательство.

   По определению 2, имеем $left|overrightarrow{b }right|=left|kright|left|overrightarrow{a }right|=0cdot left|overrightarrow{a }right|=0$, следовательно,$overrightarrow{b }=koverrightarrow{a }=overrightarrow{0}$

2. Для любого вектора $overrightarrow{a }$ и любого действительного числа $k$ векторы $overrightarrow{a }$ и $koverrightarrow{a }$ коллинеарны.

   Доказательство.

   Так как по определению 2, векторы $overrightarrow{a }$ и $koverrightarrow{a }$ сонаправлены или противоположно направлены (в зависимости от значения $k$), то они будут коллинеарны.

3. Для любых действительных чисел $m$ и $n$ и вектора $overrightarrow{a }$ справедлив сочетательный закон:

   [left(mnright)overrightarrow{a }=m(noverrightarrow{a })]

   Доказательство этого закона иллюстрирует рисунок 3.

   

   Рисунок 3. Сочетательный закон

4. Для любых действительных чисел $m$ и $n$ и вектора $overrightarrow{a }$ справедлив первый распределительный закон:

   [left(m+nright)overrightarrow{a }=moverrightarrow{a }+noverrightarrow{a }]

   Доказательство этого закона иллюстрирует рисунок 4.

   

   Рисунок 4. Первый распределительный закон

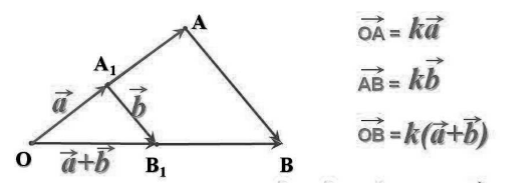
5. Для любого действительного числа $m$ и векторов $overrightarrow{a }$ и $overrightarrow{b }$ справедлив второй распределительный закон:

   [mleft(overrightarrow{a }+overrightarrow{b}right)=moverrightarrow{a }+moverrightarrow{b }]

   Доказательство этого закона иллюстрирует рисунок 5.

   

   Рисунок 5. Второй распределительный закон

«Умножение вектора на число» 👇

Пример задачи на использование понятия произведения вектора на число

Пример 1

Пусть $overrightarrow{x}=overrightarrow{a }+overrightarrow{b}$, $overrightarrow{y}=overrightarrow{a }-overrightarrow{b}$. Найти векторы:

1. $2overrightarrow{x}+2overrightarrow{y}$

2. $overrightarrow{x}+frac{1}{2}overrightarrow{y}$

3. $-overrightarrow{y}-overrightarrow{x}$

Решение.

1. $2overrightarrow{x}+2overrightarrow{y}=2left(overrightarrow{a }+overrightarrow{b}right)+2left(overrightarrow{a }-overrightarrow{b}right)=2overrightarrow{a }+2overrightarrow{b}+2overrightarrow{a }-2overrightarrow{b}=4overrightarrow{a }$

2. $overrightarrow{x}+frac{1}{2}overrightarrow{y}=overrightarrow{a }+overrightarrow{b}+frac{1}{2}left(overrightarrow{a }-overrightarrow{b}right)=overrightarrow{a }+overrightarrow{b}+frac{1}{2}overrightarrow{a }-frac{1}{2}overrightarrow{b}=frac{3}{2}overrightarrow{a }+frac{1}{2}overrightarrow{b}=frac{3overrightarrow{a }+overrightarrow{b}}{2}$

3. $-overrightarrow{y}-overrightarrow{x}=-left(overrightarrow{a }-overrightarrow{b}right)-left(overrightarrow{a }+overrightarrow{b}right)=-overrightarrow{a }+overrightarrow{b}-overrightarrow{a }-overrightarrow{b}=-2overrightarrow{a }$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 01.04.2023

Возможно ли умножение вектора на число

Произведением вектора (bar{a}), не равного нулю, на число (lambda ne 0) является вектор (lambda bar{a},) коллинеарный заданному, то есть он будет сонаправлен данному вектору (bar{a}), если (lambda>0), и противоположно направленным — если (lambda<0), а его модуль равен модулю данного вектора, умноженному на модуль числа:

(lambda >0:lambda bar{a}uparrow uparrow bar{a})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(lambda <0:lambda bar{a}uparrow downarrow bar{a})

(left|lambda bar{a}right|=left|lambda right|cdot left|bar{a}right|)

В том случае, когда вектор (bar{a}ne bar{0}) задают с помощью координат, то произведение этого вектора на число (lambda ne 0) является вектором (lambda bar{a}) с координатами, равными соответствующим координатам заданного вектора (bar{a}), умноженным на число (lambda:)

(bar{a}=left(a_{1} ;; a_{2} ;; a_{3} right)Rightarrow lambda bar{a}=left(lambda a_{1} ;; lambda a_{2} ;; lambda a_{3} right))

Особенность такого действия, как умножение вектора на число заключается в том, что число является простой численной формой величины, для которого отсутствует направление, а вектор определяется в качестве направленного отрезка, обладающего численным измерением и направлением.

Подобная операция, как и вычитание, нередко используется при решении задач в математике, геометрии и физике.

Произведение ненулевого вектора (vec{a}) на число k является таким вектором (vec{b}), длина которого составляет (left| vec{b}right|=left|k right|*left|vec{a} right|). При этом векторы (vec{a}) и (vec{b}) сонаправлены, если k больше или равно нулю, и противоположно направлены, когда k меньше нуля. Произведение нулевого вектора на любое число в результате позволяет получить ненулевой вектор.

Предположим, что существует некий вектор (vec{a}). В таком случае вектор (vec{2a}) является вектором, направленным в ту же сторону, но с длиной, которая в 2 раза превышает длину вектора (vec{a}). Длина его в два раза больше. Вектор (vec{-2a}) является вектором, который направлен противоположно вектору (vec{a}) и длиннее его в 2 раза.

Геометрическая и алгебраическая интерпретация умножения

Алгебраическая интерпретация: произведение ненулевого вектора на число представляет собой вектор с координатами, равными соответствующим координатам данного вектора, умноженным на число.

Яркий пример умножения вектора на число является второй закон Ньютона, который часто применяют при решении задач в физике. Если умножить обе части закона Ньютона на массу тела, то формула примет следующий вид:

(m*vec{a}=vec{F})

После того, как умножили массу данного тела в виде скаляра m на ускорение тела, выраженного вектором (vec{a}), в результате получили вектор (m*vec{a}). Данный вектор можно обозначить, как (vec{F}), который будет называться силой. Таким образом, под действием силы тело приобретает ускорение.

Рассматриваемая формула записана в векторном виде:

(m*vec{a}=vec{F})

В таком случае говорят не только о модулях, то есть длинах векторов. С помощью векторного вида можно определить направление вектора. Согласно рассмотренному ранее определению произведения вектора на число, результат подобной операции не влияет на направление вектора. Его нельзя повернуть на какой-либо угол путем умножения на число. Результат произведения отличается лишь длиной вектора. Таким образом, векторы (vec{a}) и (vec{F}) характеризуются одинаковым направлением, но отличается по длине. В данном случае длина векторов отличается в m раз.

Понятие, основные свойства

В том случае, когда вектор (vec{b}) равен произведению ненулевого числа k и ненулевого вектора (vec{a}), то есть (vec{b}=k*vec{a}), справедливы следующие утверждения:

• (vec{a}parallelvec{b}), то есть рассматриваемые вектора параллельны;
• (vec{a}) и (vec{b}) обладают одинаковым направлением при k больше нуля;
• (vec{a}) и (vec{b}) обладают разными направлениями при k меньше нуля.

Вектор можно умножить на число в виде скалярной величины. При этом в результате получится тоже вектор. После операции умножения длина заданного вектора изменится:

• длина вектора будет увеличена при умножении на число, модуль которого больше 1;
• длина вектора уменьшится в том случае, когда модуль числа меньше 1.

Если вектор умножить на положительное число, полученный вектор будет обладать таким же направлением, что и первоначальный. В том случае, когда предполагается произведение вектора на отрицательное число, полученный в результате вектор будет направлен в противоположную сторону.

В том случае, когда есть информация о координатах вектора, при умножении его на число следует умножить каждую координату рассматриваемого вектора на данное число.

(vec{a}=left{a_{x};a_{y} right})

Данная запись представляет собой координаты вектора (vec{a}.)

(k*vec{a}=left{k*a_{x};k*a_{y} right})

Формулы применяющиеся при перемножении вектора и числа

В случае умножения вектора на число удобно использовать формулу умножения, предназначенную для решения плоских задач. При этом произведение вектора (vec{a}=left{a_{x};a_{y} right}) и какого-то числа k вычисляют по формуле:

(k*vec{a}=left{k*a_{x};k*a_{y} right})

Если предполагается решить задачу пространственного типа на произведение вектора (vec{a}=left{a_{x};a_{y}; a_{z} right}) и числа, то целесообразно воспользоваться следующей закономерностью:

(k*vec{a}=left{k*a_{x};k*a_{y}; k*a_{z} right})

Предусмотрена формула умножения n-мерного вектора. Когда n-мерный вектор (vec{a}=left{a_{1};a_{2};…; a_{n} right}) умножают на число k, целесообразно воспользоваться формулой:

(k*vec{a}=left{k*a_{1};k*a_{2};…; k*a_{n} right})

Примеры задач с решением 

Задача 1

Дан вектор (vec{a}=left{1;2 right}). Необходимо найти произведение этого вектора на 3.

Решение

В данном случае целесообразно воспользоваться формулой для решения плоских задач:

(k*vec{a}=left{k*a_{x};k*a_{y} right})

Таким образом:

(3*vec{a}=left{3*1;3*2 right}=left{3;6 right})

Ответ: (left{3;6 right})

Задача 2

Задан пространственный вектор (vec{a}=left{1;2;-5 right}). Данный вектор необходимо умножить на число -2.

Решение

В случае пространственной задачи следует воспользоваться следующей формулой:

(k*vec{a}=left{k*a_{x};k*a_{y}; k*a_{z} right})

Подставив числовые значения, получим:

((-2)*vec{a}=left{(-2)*1;(-2)*2; (-2)*(-5) right}=left{-2;-4;10 right})

Ответ: (left{-2;-4;10 right})

Задача 3

Существует некий вектор (bar{a}=left(-1;; 2;; 3right)). Требуется найти произведение этого вектора на число 2.

Решение

Исходя из определения, для умножения заданного вектора на число (lambda =2) требуется каждую координату вектора (bar{a}) умножить на это число. Таким образом:

(2bar{a}=2cdot left(-1;; 2;; 3right)=left(2cdot left(-1right);; 2cdot 2;; 2cdot 3right)=left(-2;; 4;; 6right))

Ответ: (2cdot bar{a}=left(-2;; 4;; 6right))

Задача 4

Задан вектор (bar{a}=left(-2;; 4right)). Необходимо определить вектор (-3bar{a}).

Решение

В том случае, когда требуется найти искомое произведение, следует умножить каждую координату заданного вектора (bar{a}) на число (lambda =-3). В результате умножения вектора на число получим:

(-3bar{a}=-3cdot left(-2;; 4right)=left(-3cdot left(-2right);; -3cdot 4right)=left(6;; -12right))

Ответ: (-3bar{a}=left(6;; -12right))

Задача 5

Согласно анализу рассмотренных закономерностей, действия с векторами аналогичны действиям с алгебраическими выражениями. По этому принципу требуется упростить следующую запись:

(vec{p}=2(vec{a}-vec{b})+(vec{c}+vec{a})-3(vec{b}-vec{c}+vec{a}))

Решение

В первую очередь следует раскрыть скобки:

(vec{p}=2vec{a}-2vec{b}+vec{c}+vec{a}-3vec{b}+3vec{c}-3vec{a})

Далее необходимо привести подобные:

(vec{p}=2vec{a}+vec{a}-3vec{a}-2vec{b}-3vec{b}+vec{c}+3vec{c}=-5vec{b}+4vec{c})

Ответ: (-5vec{b}+4vec{c})

Задача 6

Имеется некий отрезок АВ. Точка С является серединой данного отрезка, точка О представляет собой произвольную точку плоскости. Также (vec{OA}=vec{a}) и (vec{OB}=vec{b}.) Требуется доказать, что:

(vec{OC}=1/2(vec{a}+vec{b}))

Решение 1

Используя правило треугольника, можно выразить вектор (vec{OC}) в виде суммы двух векторов:

(vec{OC}=vec{a}+vec{AC})

Кроме того, следует отметить, что:

(vec{OC}=vec{b}+vec{BC})

В результате получилась система двух уравнений:

(vec{OC}=vec{a}+vec{AC})

(vec{OC}=vec{b}+vec{BC})

Далее необходимо сложить уравнения системы:

(2vec{OC}=vec{a}+vec{AC}+vec{b}+vec{BC}=vec{a}+vec{b}+vec{AC}+vec{BC})

(vec{AC}+vec{BC}=vec{0})

Исходя из того, что С является серединой АВ, следует вывод: модули данных векторов равны, но они обладают разными направлениями. Таким образом, сумма векторов является нулевым вектором. В результате:

(2vec{OC}=vec{a}+vec{b})

При делении обеих частей уравнения на 2 получим:

(vec{OC}=1/2(vec{a}+vec{b}))

Уравнение доказано.

Решение 2

(vec{OC}=vec{a}+vec{AC}=vec{a}+1/2vec{AB}=vec{a}+1/2(vec{b}-vec{a}))

Следует раскрыть скобки и привести подобные:

(vec{OC}=vec{a}+1/2vec{b}-1/2vec{a}=vec{a}-1/2vec{a}+1/2vec{b}=1/2(vec{a}+vec{b}))

Уравнение доказано.

Задача 7

Требуется доказать, что средняя линия трапеции и ее основания параллельны друг другу, а также средняя линия трапеции равна половине суммы оснований.

Решение

Известно, что средней линией трапеции соединены ее боковые стороны. Основания трапеции параллельны друг другу. Согласно правилу многоугольника, можно выразить вектор vec{MN} как сумму векторов:

(vec{MN}=vec{MB}+vec{BC}+vec{CN})

С другой стороны:

(vec{MN}=vec{MA}+vec{AD}+vec{DN})

В результате получена система уравнений:

(vec{MN}=vec{MB}+vec{BC}+vec{CN})

(vec{MN}=vec{MA}+vec{AD}+vec{DN})

Следует сложить уравнения системы:

(2vec{MN}=vec{MB}+vec{BC}+vec{CN}+vec{MA}+vec{AD}+vec{DN}=vec{MB}+vec{MA}+vec{BC}+ vec{AD}+vec{CN}+vec{DN})

Векторы (vec{MB}) и (vec{MA}) обладают противоположными направлениями и в сумме дают нулевой вектор, так как М — середина АВ, то есть модули данных векторов равны, кроме того, они противонаправлены. Аналогично векторы (vec{CN}) и (vec{DN}) дают в сумме нулевой вектор. Таким образом, получаем:

(2vec{MN}=vec{BC}+vec{AD})

Затем можно поделить обе части уравнения на 2:

(vec{MN}=1/2(vec{BC}+vec{AD}))

В результате получено доказательство того, что средняя линия равна половине суммы оснований. Кроме того, прямая MN параллельна основаниям трапеции.

Кроме складывания и вычитания векторов существует ещё одна, последняя линейная операция над векторами. Это умножение векторов на числа. Числа мы будем здесь рассматривать только действительные. При умножении вектора на число, в общем случае может изменится как длина, так и направление исходного вектора. Общее правило такое:

Правило умножения вектора на число

При умножении вектора a⃗vec{a} на число λlambda получаем вектор λa⃗lambda vec{a}. Длина этого вектора ∣λa⃗∣=∣λ∣∣a⃗∣|lambdavec{a}|=|lambda||vec{a}|. Направление вектора λa⃗lambda vec{a} совпадает с направлением вектора a⃗vec{a} при λ>0lambda>0, и противоположно вектору a⃗vec{a} если λ<0lambda<0.

Рассмотрим пару примеров.

Пример 1

λ=0lambda=0.
Тогда λa⃗=0⋅a⃗=0⃗lambda vec{a}=0cdot vec{a}=vec{0}. То есть, умножение любого вектора a⃗vec{a} на число ноль дает нулевой вектор (о том, что это за вектор речь шла в статье Понятие вектора). Часто стрелочку над нулем не пишут и обозначают просто: 0⋅a⃗=00cdot vec{a}=0.

Пример 2

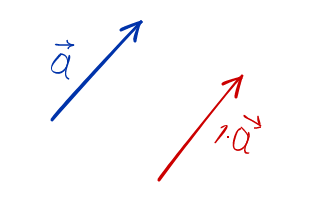
λ=1lambda=1.
Тогда λa⃗=1⋅a⃗=a⃗lambda vec{a}=1cdot vec{a}=vec{a}. Умножение любого вектора a⃗vec{a} на единицу никак не изменяет вектор a⃗vec{a}.

Пример 3

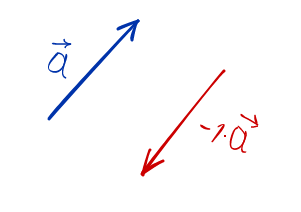
λ=−1lambda=-1.
Тогда λa⃗=−1⋅a⃗=−a⃗lambda vec{a}=-1cdot vec{a}=-vec{a}. Умножение любого вектора a⃗vec{a} на минус единицу меняет направление вектора a⃗vec{a} на противоположное, но никак не влияет на длину вектора aa. То есть, эта операция ставит вектору a⃗vec{a} в соответствие вектор −a⃗-vec{a}.

Пример 4

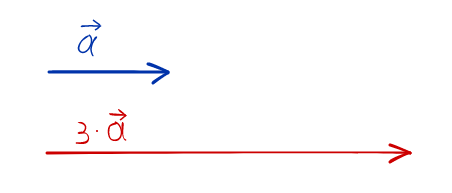
λ=3lambda=3.
Получаем: λa⃗=3⋅a⃗lambda vec{a}=3cdot vec{a}. Получим вектор, длина которого в три раза больше исходного. Так как 3>03>0, то направление вектора 3⋅a⃗3cdot vec{a} совпадает с направлением вектора a⃗vec{a}.

Пример 5

λ=−110lambda=-frac{1}{10}.
Получаем λa⃗=−110⋅a⃗lambda vec{a}=-frac{1}{10}cdot vec{a}. В результате, получим вектор, длина которого в десять раз меньше вектора a⃗vec{a}. Поскольку −110<0-frac{1}{10}<0, то направление вектора −110⋅a⃗-frac{1}{10}cdot vec{a} противоположно направлению вектора a⃗vec{a}.

Рисунок здесь попробуйте нарисовать сами.

Для умножения векторов на числа имеют место следующие свойства:

Свойства умножения векторов на числа

Ассоциативность умножения вектора на число:
λ(μa⃗)=(λμ)a⃗lambda(mu vec{a})=(lambdamu)vec{a}
Дистрибутивность умножения вектора на число относительно сложения чисел:
(λ+μ)a⃗=λa⃗+μa⃗(lambda+mu)vec{a}=lambdavec{a}+muvec{a}
Дистрибутивность умножения вектора на число относительно сложения векторов:
λ(a⃗+b⃗)=λa⃗+λb⃗lambda(vec{a}+vec{b})=lambdavec{a}+lambdavec{b}

Может возникнуть вопрос, для чего нам вообще нужно умножать векторы на числа. Дело в том, что эта операция, вместе с двумя другими линейными операциями над векторами (сложение и вычитание) представляет собой возможность получать новые векторы из уже данных нам. Например, во втором законе Ньютона в векторной форме:

2-й закон Ньютона

ma⃗=F⃗mvec{a}=vec{F},

где

mm — масса тела;
a⃗vec{a} — вектор ускорения тела;
F⃗vec{F} — приложенный вектор силы к телу.

масса mm тела умножается на его ускорение a⃗vec{a}. Вот вам и пример умножения вектора на число.

Тест по теме «Умножение вектора на число»