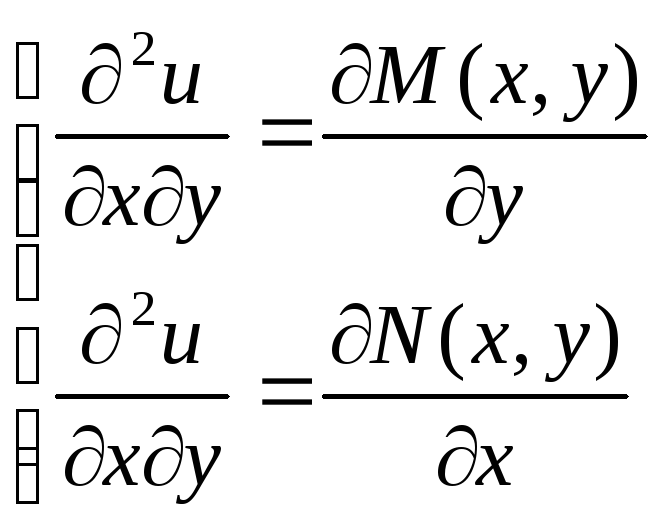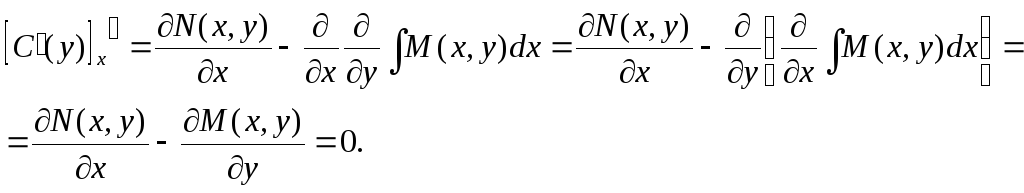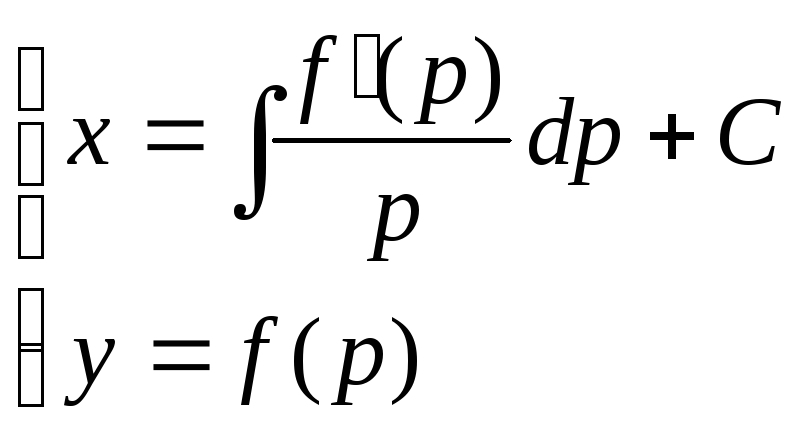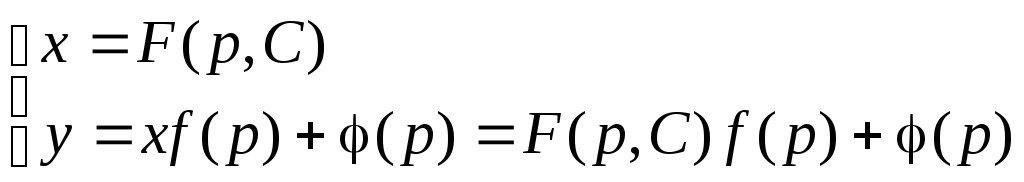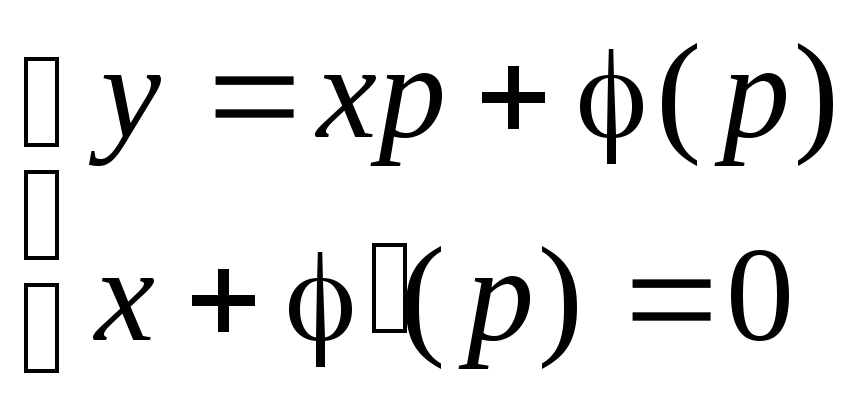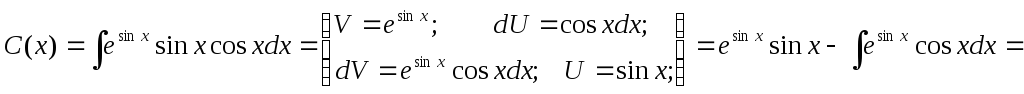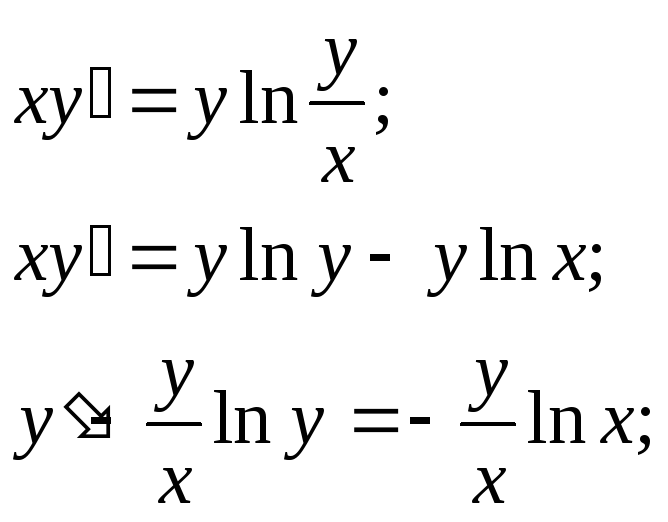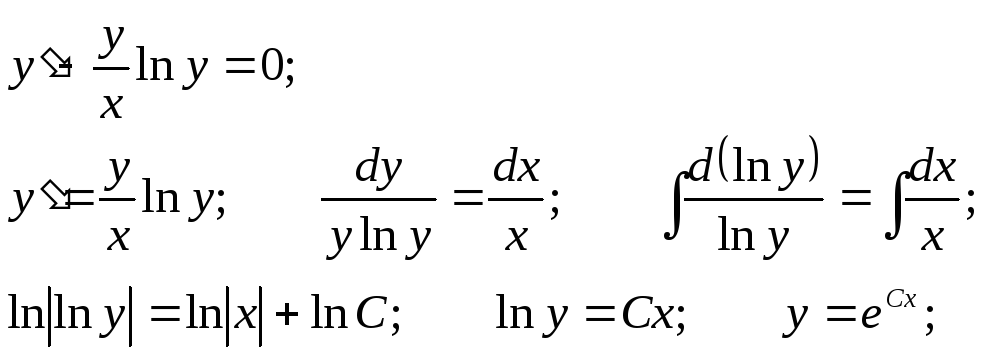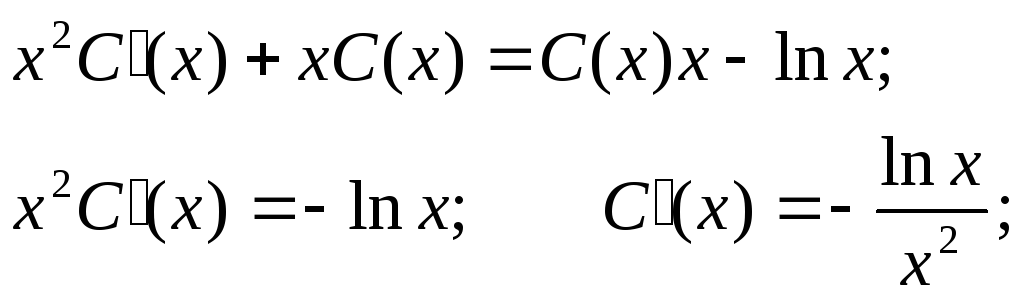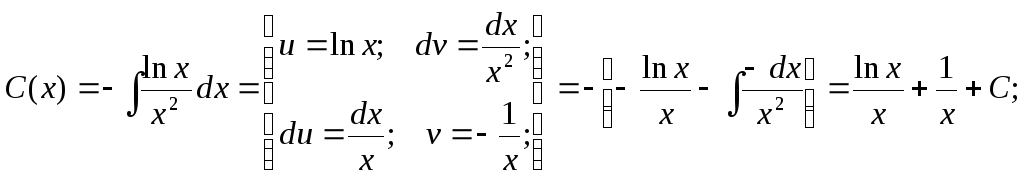Как найти уравнение бернулли

Уравнение Бернулли.

Определение.
Уравнением Бернулли называется уравнение
вида

где
P
и Q
– функции от х
или постоянные числа, а n
– постоянное число, не равное 1.

Для
решения уравнения Бернулли применяют
подстановку
,
с помощью которой, уравнение Бернулли
приводится к линейному.

Для
этого разделим исходное уравнение на
yn.

Применим
подстановку, учтя, что
.

Т.е.
получилось линейное уравнение относительно
неизвестной функции z.

Решение
этого уравнения будем искать в виде:

Пример.
Решить
уравнение

Разделим
уравнение на xy2:

Полагаем

.

Полагаем

Произведя
обратную подстановку, получаем:

Пример.
Решить уравнение

Разделим
обе части уравнения на

Полагаем

Получили
линейное неоднородное дифференциальное
уравнение. Рассмотрим соответствующее
ему линейное однородное уравнение:

Полагаем
C
= C(x)
и подставляем полученный результат в
линейное неоднородное уравнение, с
учетом того, что:

Получаем:

Применяя
обратную подстановку, получаем
окончательный ответ:

Уравнения
в полных дифференциалах
(тотальные).

Определение.
Дифференциальное уравнение первого
порядка вида:

называется
уравнением в полных дифференциалах,
если левая часть этого уравнения
представляет собой полный дифференциал
некоторой функции

Интегрирование
такого уравнения сводится к нахождению
функции u,
после чего решение легко находится в
виде:

Таким
образом, для решения надо определить:

1) В каком случае левая часть уравнения представляет собой полный дифференциал функции u;

2) Как найти эту функцию.

Если
дифференциальная форма
является
полным дифференциалом некоторой функции
u,
то можно записать:

Т.е.
.

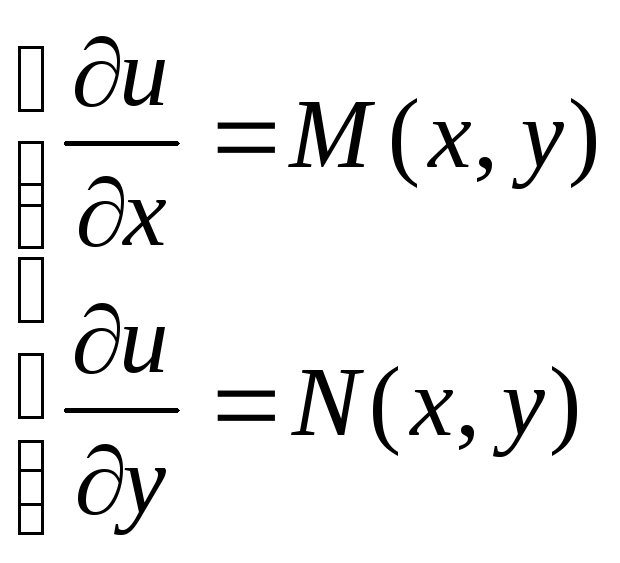
Найдем
смешанные производные второго порядка,
продифференцировав первое уравнение
по у,
а второе – по х:

Приравнивая
левые части уравнений, получаем
необходимое
и достаточное условие
того, что левая часть дифференциального
уравнения является полным дифференциалом.
Это условие также называется условием
тотальности.

Теперь
рассмотрим вопрос о нахождении собственно
функции u.

Проинтегрируем
равенство
:

Вследствие
интегрирования получаем не постоянную
величину С, а некоторую функцию С(у),
т.к. при интегрировании переменная у
полагается постоянным параметром.

Определим
функцию С(у).

Продифференцируем
полученное равенство по у.

Откуда
получаем:

Для
нахождения функции С(у) необходимо
проинтегрировать приведенное выше
равенство. Однако, перед интегрированием
надо доказать, что функция С(у) не зависит
от х.
Это условие будет выполнено, если
производная этой функции по х
равна нулю.

Теперь
определяем функцию С(у):

Подставляя
этот результат в выражение для функции
u,
получаем:

Тогда
общий интеграл исходного дифференциального
уравнения будет иметь вид:

Следует
отметить, что при решении уравнений в
полных дифференциалах не обязательно
использовать полученную формулу. Решение
может получиться более компактным, если
просто следовать методу, которым формула
была получена.

Пример.
Решить уравнение

Проверим
условие тотальности:

Условие
тотальности выполняется, следовательно,
исходное дифференциальное уравнение
является уравнением в полных дифференциалах.

Определим
функцию u.

;

Итого,

Находим
общий интеграл исходного дифференциального
уравнения:

Уравнения
вида y
= f(y’)
и
x
= f(y’).

Решение
уравнений, не содержащих в одном случае
аргумента х,
а в другом – функции у,
ищем в параметрической форме, принимая
за параметр производную неизвестной
функции.

Для
уравнения первого типа получаем:

Делая
замену, получаем:

В
результате этих преобразований имеем
дифференциальное уравнение с разделяющимися
переменными.

Общий
интеграл в параметрической форме
представляется системой уравнений:

Исключив
из этой системы параметр р,
получим общий интеграл и не в параметрической
форме.

Для
дифференциального
уравнения вида x
= f(y’)
с помощью той же самой подстановки и
аналогичных рассуждений получаем
результат:

Уравнения Лагранжа
и Клеро.

(
Алекси Клод Клеро (1713 – 1765) французский
математик

ин.
поч. член Петерб. АН )

Определение.
Уравнением
Лагранжа называется
дифференциальное уравнение, линейное
относительно х
и у,
коэффициенты которого являются функциями
от y’.

Для
нахождения общего решение применяется
подстановка p
= y’.

Дифференцируя
это уравнение,c
учетом того, что
,
получаем:

Если
решение этого (линейного относительно
х)
уравнения есть
то
общее решение уравнения Лагранжа может
быть записано в виде:

Определение.
Уравнением Клеро называется
уравнение первой степени (т.е. линейное)
относительно функции и аргумента вида:

Вообще
говоря, уравнение Клеро является частным
случаем уравнения Лагранжа.

С
учетом замены
,
уравнение принимает вид:

Это
уравнение имеет два возможных решения:

или

Впервом случае:

Видно,
что общий интеграл уравнения Клеро
представляет собой семейство прямых
линий.

Во
втором случае решение в параметрической
форме выражается системой уравнений:

Исключая
параметр р,
получаем второе решение F(x,
y)
= 0. Это решение не содержит произвольной
постоянной и не получено из общего
решения, следовательно, не является
частным решением.

Это
решение будет являться особым интегралом.
( См. Особое
решение.
)

Далее рассмотрим
примеры решения различных типов
дифференциальных уравнений первого
порядка.

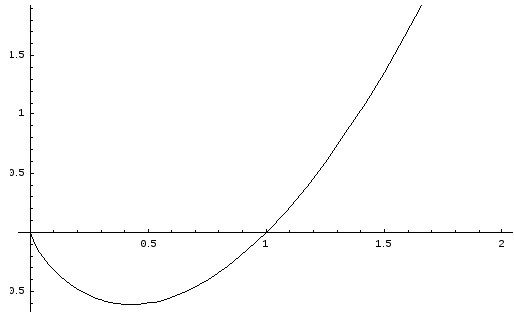
Пример.
Решить уравнение с заданными начальными
условиями.

Это
линейное неоднородное дифференциальное
уравнение первого порядка.

Решим
соответствующее ему однородное уравнение.

Для
неоднородного уравнения общее решение
имеет вид:

Дифференцируя,
получаем:

Для
нахождения функции С(х) подставляем
полученное значение в исходное
дифференциальное уравнение:

Итого,
общее решение:

C
учетом начального условия
определяем
постоянный коэффициентC.

Окончательно
получаем:

Для
проверки подставим полученный результат
в исходное дифференциальное уравнение:


верно

Ниже показан график
интегральной кривой уравнения.

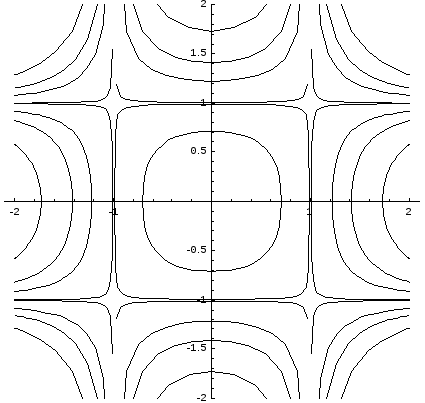
Пример.
Найти общий интеграл уравнения
.

Это
уравнение с разделяющимися переменными.

Общий
интеграл имеет вид:

Построим интегральные
кривые дифференциального уравнения
при различных значениях С.

С
= — 0,5 С = -0,02 С = -1 С = -2

С
= 0,02 С = 0,5 С = 1 С = 2

Пример.
Найти решение дифференциального
уравнения, удовлетворяющее заданным
начальным условиям.

Это
уравнение с разделяющимися переменными.

Общее
решение имеет вид:

Найдем
частное решение при заданном начальном
условии у(0)
= 0.

Окончательно
получаем:

Пример.
Решить предыдущий пример другим
способом.

Действительно,
уравнение
может быть рассмотрено как линейное
неоднородное дифференциальное уравнение.

Решим
соответствующее ему линейное однородное
уравнение.

Решение
неоднородного уравнения будет иметь
вид:

Тогда

Подставляя
в исходное уравнение, получаем:

Итого

С
учетом начального условия у(0) = 0 получаем

Как видно результаты,
полученные при решении данного
дифференциального уравнения различными
способами, совпадают.

При решении
дифференциальных уравнений бывает
возможно выбирать метод решения, исходя
из сложности преобразований.

Пример.
Решить уравнение
с
начальным условием у(0) = 0.

Это
линейное неоднородное уравнение. Решим
соответствующее ему однородное уравнение.

Для
линейного неоднородного уравнения
общее решение будет иметь вид:

Для
определения функции С(х) найдем производную
функции у
и подставим ее в исходное дифференциальное
уравнение.

Итого

Проверим полученное
общее решение подстановкой в исходное
дифференциальное уравнение.

(верно)

Найдем
частное решение при у(0) = 0.

Окончательно

Пример.
Найти решение дифференциального
уравнения

с
начальным условием у(1) = 1.

Это
уравнение может быть преобразовано и
представлено как уравнение с разделенными
переменными.

С
учетом начального условия:

Окончательно

Пример.
Решить дифференциальное уравнение
с начальным условием у(1) = 0.

Это
линейное неоднородное уравнение.

Решим
соответствующее ему однородное уравнение.

Решение
неоднородного уравнения будет иметь
вид:

Подставим
в исходное уравнение:

Общее
решение будет иметь вид:

C
учетом начального условия у(1) = 0:

Частное
решение:

Пример.
Найти решение дифференциального
уравнения
с начальным условием у(1) = е.

Это уравнение
может быть приведено к виду уравнения
с разделяющимися переменными с помощью
замены переменных.

Обозначим:

Уравнение
принимает вид:

Получили уравнение с
разделяющимися переменными.

Сделаем
обратную замену:

Общее
решение:

C
учетом начального условия у(1) = е:

Частное
решение:

Второй
способ решения.

Получили
линейное неоднородное дифференциальное
уравнение. Соответствующее однородное:

Решение
исходного уравнения ищем в виде:

Тогда

Подставим
полученные результаты в исходное
уравнение:

Получаем
общее решение:

Пример.
Решить дифференциальное уравнение
с начальным условием у(1)=0.

В
этом уравнении также удобно применить
замену переменных.

Уравнение
принимает вид:

Делаем
обратную подстановку:

Общее
решение:

C
учетом начального условия у(1) = 0:

Частное
решение:

Второй
способ решения.

Замена
переменной:

Общее
решение:

Источник
Автор статьи

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Характеристика уравнения Бернулли

Определение 1

Дифференциальное уравнение первого порядка, имеющее стандартный вид $y’+Pleft(xright)cdot y=Qleft(xright)cdot y^{n}$, где $Pleft(xright)$ и $Qleft(xright)$ — непрерывные функции, а $n$ — некоторое число, называется дифференциальным уравнением Якоба Бернулли.

При этом на число $n$ накладываются ограничения:

  • $nne 0$, так как при $n = 0$ дифференциальное уравнение представляет собой линейное неоднородное, и какой-то иной специальный метод решения в этом случае не нужен;
  • $nne 1$, так как если мы имеем в качестве $n$ единицу, дифференциальное уравнение представляет собой линейное однородное, метод решения которого также известен.

Кроме того, не рассматривается специально тривиальное решение дифференциального уравнения Бернулли $y=0$.

Не следует путать дифференциальное уравнение математика Якоба Бернулли с законом Бернулли, названным в честь дяди его племянника, известного как Даниил Бернулли.

Замечание 1

Даниил Бернулли — физик, наиболее известная найденная им закономерность состоит в описании взаимосвязи скорости потока жидкости и давления. Закон Бернулли также применим и для ламинарных течений газа. В целом он применяется в гидравлике и гидродинамике.

Решение уравнения Бернулли сведением к линейному неоднородному

Основной метод решения дифференциального уравнения Бернулли состоит в том, что посредством преобразований оно приводится к линейному неоднородному. Эти преобразования следующие:

  1. Умножаем уравнение на число $y^{-n} $ и получаем $y^{-n} cdot y’+Pleft(xright)cdot y^{1-n} =Qleft(xright)$.
  2. Применяем замену $z=y^{1-n} $ и дифференцируем это равенство как сложную степенную функцию; получаем $z’=left(1-nright)cdot y^{-n} cdot y’$, откуда $frac{z’}{1-n} =y^{-n} cdot y’$.
  3. Подставляем значения $y^{1-n} $ и $y^{-n} cdot y’$ в данное дифференциальное уравнение и получаем $frac{z’}{1-n} +Pleft(xright)cdot z=Qleft(xright)$ или $z’+left(1-nright)cdot Pleft(xright)cdot z=left(1-nright)cdot Qleft(xright)$.

«Уравнение Бернулли» 👇

Полученное дифференциальное уравнение является линейным неоднородным относительно функции $z$, которое решаем следующим образом:

  1. Вычисляем интеграл $I_{1} =int left(1-nright)cdot Pleft(xright)cdot dx $, записываем частное решение в виде $vleft(xright)=e^{-I_{1} } $, выполняем упрощающие преобразования и выбираем для $vleft(xright)$ простейший ненулевой вариант.
  2. Вычисляем интеграл $I_{2} =int frac{left(1-nright)cdot Qleft(xright)}{vleft(xright)} cdot dx $, посля чего записываем выражение в виде $uleft(x,Cright)=I_{2} +C$.
  3. Записываем общее решение линейного неоднородного дифференциального уравнения в виде $z=uleft(x,Cright)cdot vleft(xright)$.
  4. Возвращаемся к функции $y$, заменяя $z$ на $y^{1-n} $, и при необходимости выполняем упрощающие преобразования.

Пример:

Найти общее решение дифференциального уравнения $frac{dy}{dx} +frac{y}{x} =y^{2} cdot left(4-x^{2} right)$. Записать частное решение, удовлетворяющее начальному условию $y=1$ при $x=1$.

В данном случае имеем дифференциальное уравнение Бернулли, представленное в стандартном виде.

При этом $n=2$, $Pleft(xright)=frac{1}{x} $, $Qleft(xright)=4-x^{2} $.

Представляем его в форме относительно замены $z$:

$z’+left(1-2right)cdot frac{1}{x} cdot z=left(1-2right)cdot left(4-x^{2} right)$ или $z’-frac{1}{x} cdot z=-left(4-x^{2} right)$.

Полученное дифференциальное уравнение является линейным неоднородным относительно функции $z$, которое решаем описанным выше методом.

Вычисляем интеграл $I_{1} =int left(1-nright)cdot Pleft(xright)cdot dx $.

Имеем $I_{1} =int left(1-2right)cdot frac{1}{x} cdot dx =-ln left|xright|$.

Записываем частное решение в виде $vleft(xright)=e^{-I_{1} } $ и выполняем упрощающие преобразования: $vleft(xright)=e^{ln left|xright|} $; $ln vleft(xright)=ln left|xright|$; $vleft(xright)=left|xright|$.

Выбираем для $vleft(xright)$ простейший ненулевой вариант: $vleft(xright)=x$.

Вычисляем интеграл $I_{2} =int frac{left(1-nright)cdot Qleft(xright)}{vleft(xright)} cdot dx $.

Имеем:

Записываем выражение в виде $uleft(x,Cright)=I_{2} +C$, то есть $uleft(x,Cright)=frac{x^{2} }{2} -4cdot ln left|xright|+C$.

Окончательно записываем общее решение линейного неоднородного дифференциального уравнения относительно функции $z$ в виде $z=uleft(x,Cright)cdot vleft(xright)$, то есть $z=frac{x^{3} }{2} -4cdot xcdot ln left|xright|+Ccdot x$.

Теперь возвращаемся к функции $y$, заменяя $z$ на $y^{1-n} $:

$y^{1-2} =frac{x^{3} }{2} -4cdot xcdot ln left|xright|+Ccdot x$ или $frac{1}{y} =frac{x^{3} }{2} -4cdot xcdot ln left|xright|+Ccdot x$.

Это и есть общее решение данного дифференциального уравнения Бернулли, записанное в неявной форме.

Для поиска частного решения используем данное начальное условие $y=1$ при $x=1$:

Следовательно, частное решение имеет вид: $frac{1}{y} =frac{x^{3} }{2} -4cdot xcdot ln left|xright|+frac{x}{2} $.

Решение дифференциального уравнения Бернулли методом подстановки

Второе возможное решение уравнения Бернулли состоит в методе подстановки.

Пример:

Найти общее решение дифференциального уравнения $y’+frac{y}{x} =y^{2} cdot left(4-x^{2} right)$ методом подстановки.

Применяем подстановку $y=ucdot v$.

После дифференцирования получаем:

Функцию $vleft(xright)$ находим из уравнения $v’+frac{v}{x} =0$, для этого переносим второе слагаемое в правую часть.

Получаем:

$frac{dv}{dx} =-frac{v}{x} $;

разделяем переменные $frac{dv}{v} =-frac{dx}{x} $;

интегрируем $ln left|vright|=-ln left|xright|$, откуда $v=frac{1}{x} $.

Функцию $uleft(xright)$ находим из уравнения $u’cdot frac{1}{x} =u^{2} cdot frac{1}{x^{2} } cdot left(4-x^{2} right)$, в котором учтено $v=frac{1}{x} $ и $v’+frac{v}{x} =0$.

После простых преобразований получаем: $u’=u^{2} cdot frac{1}{x} cdot left(4-x^{2} right)$.

Разделяем переменные: $frac{du}{u^{2} } =frac{1}{x} cdot left(4-x^{2} right)cdot dx$.

Интегрируем: $-frac{1}{u} =4cdot ln left|xright|-frac{x^{2} }{2} +C$ или $frac{1}{u} =frac{x^{2} }{2} -4cdot ln left|xright|+C$.

Возвращаемся к старой переменной. Учитываем, что $y=ucdot v$ или $y=ucdot frac{1}{x} $, откуда $u=xcdot y$.

Получаем общее решение данного дифференциального уравнения: $frac{1}{y} =frac{x^{3} }{2} -4cdot xcdot ln left|xright|+Ccdot x$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Линейные дифференциальные уравнения 1-го порядка
и уравнение Бернулли

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Оно имеет вид

frac{dy}{dx}+p(x)y=q(x),

(1)

где p(x) и q(x) — заданные функции от x, непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если q(x)equiv0, то уравнение (1) называется линейным однородным. Оно является уравнением с разделяющимися переменными и имеет общее решение

y=Cexp!left(-int{p(x)},dxright)!,

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной, который состоит в том, что решение уравнения (1) ищется в виде

y=C(x)exp!left(-int{p(x)},dxright), где C(x) — новая неизвестная функция от x.

Пример 1. Решить уравнение y'+2xy=2xe^{-x^2}.

Решение. Применим метод вариации постоянной. Рассмотрим однородное уравнение y'+2xy=0, соответствующее данному неоднородному уравнению. Это уравнение с разделяющимися переменными. Его общее решение имеет вид y=Ce^{-x^2}.

Общее решение неоднородного уравнения ищем в виде y=C(x)e^{-x^2}, где C(x) — неизвестная функция от x. Подставляя, получаем C'(x)=2x, откуда C(x)=x^2+C. Итак, общее решение неоднородного уравнения будет y=(x^2+C)e^{-x^2}, где C — постоянная интегрирования.

Замечание. Может оказаться, что дифференциальное уравнение линейно относительно x как функция от y. Нормальный вид такого уравнения

frac{dx}{dy}+r(y)x=varphi(y).

Пример 2. Решить уравнение frac{dy}{dx}=frac{1}{xcos{y}+sin2y}.

Решение. Данное уравнение является линейным, если рассматривать x как функцию от y:

frac{dx}{dy}-xcos{y}=sin{2y}.

Применяем метод вариации произвольной постоянной. Сначала решаем соответствующее однородное уравнение

frac{dx}{dy}-xcos{y}=0,

которое является уравнением с разделяющимися переменными. Его общее решение имеет вид x=Ce^{sin{y}},~C=text{const}.

Общее решение уравнения ищем в виде x=C(y)e^{sin{y}}, где C(y) — неизвестная функция от y. Подставляя, получаем

C'(y)e^{sin{y}}=sin2y или C'(y)=e^{-sin{y}}sin2y.

Отсюда, интегрируя по частям, будем иметь

begin{aligned}C(y)&=int{e^{-sin{y}}sin2y},dy=2int{e^{-sin{y}}cos{y}sin{y}},dy=2intsin{y},d(-e^{-sin{y}})=\ &=-2sin{y},e^{-sin{y}}+2int{e^{-sin{y}}cos{y}},dy=C-2(sin{y}+1)e^{-sin{y}},end{aligned}

итак,

C(y)=-2e^{-sin{y}}(1+sin{y})+C.

(6)

Подставляя это уравнение в x=C(y)e^{sin{y}}, получаем общее решение исходного уравнения, а значит, и данного уравнения:

x=Ce^{sin{y}}-2(1+sin{y})

Исходное уравнение может быть проинтегрировано также следующим образом. Полагаем

y=u(x)v(x),

(7)

где u(x) и v(x) — неизвестные функции от x, одна из которых, например v(x), может быть выбрана произвольно.

Подставляя y=u(x)v(x) в frac{dy}{dx}+p(x)y=q(x), после преобразования получаем

vu'+(pv+v')u=q(x).

(8)

Определяя v(x) из условия v'+pv=0, найдем затем из vu'+(pv+v')u=q(x) функцию u(x), а следовательно, и решение y=uv уравнения frac{dy}{dx}+p(x)y=q(x). В качестве v(x) можно взять любое частое решение уравнения v'+pv=0,~vnotequiv0.

Пример 3. Решить задачу Коши: x(x-1)y'+y=x^2(2x-1),~y|_{x=2}=4.

Решение. Ищем общее решение уравнения в виде y=u(x)v(x); имеем y'=u'v+uv'. Подставляя выражение для y и y' в исходное уравнение, будем иметь

x(x-1)(u'v+uv')+uv=x^2(2x-1) или x(x-1)vu'+[x(x-1)v'+v]u=x^2(2x-1)

Функцию v=v(x) находим из условия x(x-1)v'+v=0. Беря любое частное решение последнего уравнения, например v=frac{x}{x-1}, и подставляя его, получаем уравнение u'=2x-1, из которого находим функцию u(x)=x^2-x+C. Следовательно, общее решение уравнения x(x-1)y'+y=x^2(2x-1) будет

y=uv=(x^2-x+C)frac{x}{x-1}, или y=frac{Cx}{x-1}+x^2.

Используя начальное условие y|_{x=2}=4, получаем для нахождения C уравнение 4=frac{2C}{2-1}+2^2, откуда C=0; так что решением поставленной задачи Коши будет функция y=x^2.

Пример 4. Известно, что между силой тока i и электродвижущей силой E в цепи, имеющей сопротивление R и самоиндукцию L, существует зависимость E=Ri+Lfrac{di}{dt}, где R и L — постоянные. Если считать E функцией времени t, то получим линейное неоднородное уравнение для силы тока i:

frac{di}{dt}+frac{R}{L}i(t)=frac{E(t)}{L}.

Найти силу тока i(t) для случая, когда E=E_0=text{const} и i(0)=I_0.

Решение. Имеем frac{di}{dt}+frac{R}{L}i(t)=frac{E_0}{L},~i(0)=I_0. Общее решение этого уравнения имеем вид i(t)=frac{E_0}{R}+Ce^{-(R/L)t}. Используя начальное условие (13), получаем из C=I_0-frac{E_0}{R}, так что искомое решение будет

i(t)=frac{E_0}{R}+left(I_0-frac{E_0}{R}right)!e^{-(R/L)t}.

Отсюда видно, что при tto+infty сила тока i(t) стремится к постоянному значению frac{E_0}{R}.

Пример 5. Дано семейство C_alpha интегральных кривых линейного неоднородного уравнения y'+p(x)y=q(x).

Показать, что касательные в соответственных точках к кривым C_alpha, определяемым линейным уравнением, пересекаются в одной точке (рис. 13).

Касательные к кривым, определяемым линейным дифференциальным уравнением

Решение. Рассмотрим касательную к какой-либо кривой C_alpha в точке M(x,y).Уравнение касательной в точке M(x,y) имеет вид

eta-q(x)(xi-x)=y[1-p(x)(xi-x)], где xi,eta — текущие координаты точки касательной.

По определению, в соответственных точках x является постоянным, а y переменным. Беря любые две касательные к линиям C_alpha в соответственных точках, для координат точки S их пересечения, получаем

xi=x+frac{1}{p(x)}, quad eta=x+frac{q(x)}{p(x)}.

Отсюда видно, что все касательные к кривым C_alpha в соответственных точках (x фиксировано) пересекаются в одной и той же точке

S!left(x+frac{1}{p(x)};,x+frac{q(x)}{p(x)}right).

Исключая в системе аргумент x, получаем уравнение геометрического места точек S colon f(xi,eta)=0.

Пример 6. Найти решение уравнения y'-y=cos{x}-sin{x}, удовлетворяющее условию: y ограничено при yto+infty.

Решение. Общее решение данного уравнения y=Ce^x+sin{x}. Любое решение уравнения, получаемое из общего решения при Cne0, будет неограниченно, так как при xto+infty функция sin{x} ограничена, а e^xto+infty. Отсюда следует, что данное уравнение имеет единственное решение y=sin{x}, ограниченное при xto+infty, которое получается из общего решения при C=0.

Уравнение Бернулли

Дифференциальное уравнение Бернулли имеет вид

frac{dy}{dx}+p(x)y=q(x)y^n, где nne0;1 (при n=0 и n=1 это уравнение является линейным).

С помощью замены переменной z=frac{1}{y^{n-1}} уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.

Пример 7. Решить уравнение Бернулли y'-xy=-xy^3.

Решение. Делим обе части уравнения на y^3:

frac{y'}{y^3}-frac{x}{y^2}=-x

Делаем замену переменной frac{1}{y^2}=zRightarrow-frac{2y'}{y^3}=z', откуда frac{y'}{y^3}=-frac{z'}{2}. После подстановки последнее уравнение обратится в линейное уравнение

-frac{z'}{2}-xz=-x или z'+2xz=2x, общее решение которого z=1+Ce^{-x^2}.

Отсюда получаем общий интеграл данного уравнения

frac{1}{y^2}=1+Ce^{-x^2} или y^2(1+Ce^{-x^2})=1.

Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как и линейное уравнение, и с помощью подстановки y(x)=u(x)v(x).

Пример 8. Решить уравнение Бернулли xy'+y=y^2ln{x}..

Решение. Применим метод вариации произвольной постоянной. Общее решение соответствующего однородного уравнения xy'+y=0 имеет вид y=frac{C}{x}. Общее решение уравнения ищем в виде y=frac{C(x)}{x}, где C(x) — новая неизвестная функция. Подставляя в исходное уравнение, будем иметь

C'(x)=C^2(x)frac{ln{x}}{x^2}.

Для нахождения функции C(x) получим уравнение с разделяющимися переменными, из которого, разделяя переменные и интегрируя, найдем

frac{1}{C(x)}=frac{ln{x}}{x}+frac{1}{x}+C~Rightarrow~C(x)=frac{x}{1+Cx+ln{x}}.

Итак, общее решение исходного уравнения y=frac{1}{1+Cx+ln{x}}.

Некоторые нелинейные уравнения первого порядка с помощью удачно найденной замены переменных сводятся к линейным уравнениям или к уравнениям Бернулли.

Пример 9. Решить уравнение y'+sin{y}+xcos{y}+x=0.

Решение. Запишем данное уравнение в виде y'+2sinfrac{y}{2}cosfrac{y}{2}+2xcos^2frac{y}{2}=0..

Деля обе части уравнения на 2cos^2frac{y}{2}, получаем frac{y'}{2cos^2dfrac{y}{2}}+operatorname{tg}frac{y}{2}+x=0.

Замена operatorname{tg}frac{y}{2}=zRightarrowfrac{dz}{dx}=frac{y'}{cos^2dfrac{y}{2}} приводит это уравнение к линейному frac{dz}{dx}+z=-x, общее решение которого z=1-x+Ce^{-x}.

Заменяя z его выражением через y, получаем общий интеграл данного уравнения operatorname{tg}frac{y}{2}=1-x+Ce^{-x}.

В некоторых уравнениях искомая функция y(x) может находиться под знаком интеграла. В этих случаях иногда удается путем дифференцирования свести данное уравнение к дифференциальному.

Пример 10. Решить уравнение xintlimits_{x}^{0}y(t),dt=(x+1)intlimits_{0}^{x}ty(t),dt,~x>0.

Решение. Дифференцируя обе части этого уравнения по x, получаем

intlimits_{0}^{x}y(t),dt+xy(x)=intlimits_{0}^{x}ty(t),dt+x(x+1)y(x) или intlimits_{0}^{x}y(t),dx=intlimits_{0}^{x}ty(t),dt+x^2y(x).

Дифференцируя еще раз по x, будем иметь линейное однородное уравнение относительно y(x)colon

y(x)=xy(x)+x^2y'(x)+2xy(x) или x^2y'(x)+(3x-1)y(x)=0.

Разделяя переменные и интегрируя, найдем y=frac{C}{x^3}e^{-1/x}. Это решение, как легко проверить, удовлетворяет исходному уравнению.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти скорость по формуле силы лоренца
  • Как исправить вальгус стопы у взрослого
  • Песня такую как ты не найти родная
  • Как найти косинус если известно число
  • Как найти общий язык по гороскопу