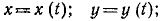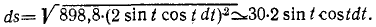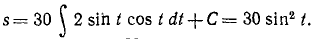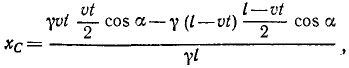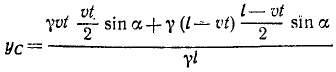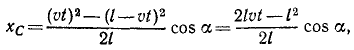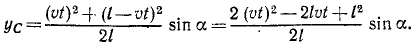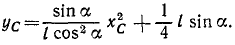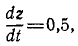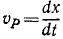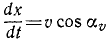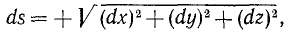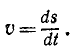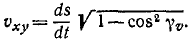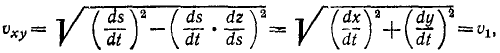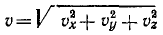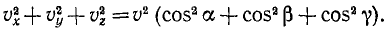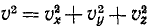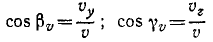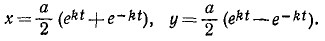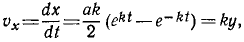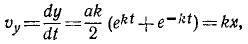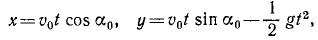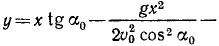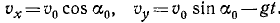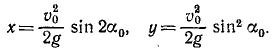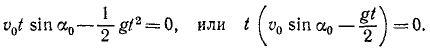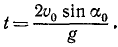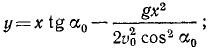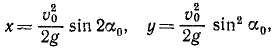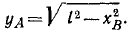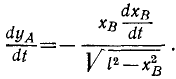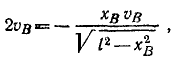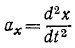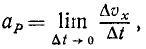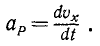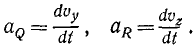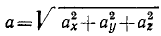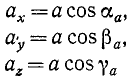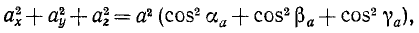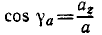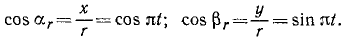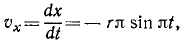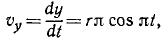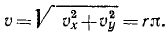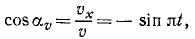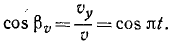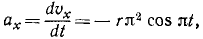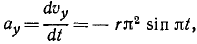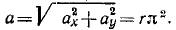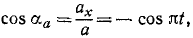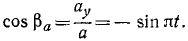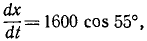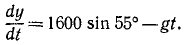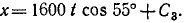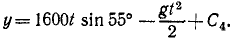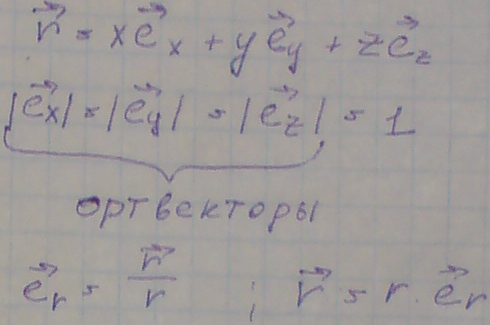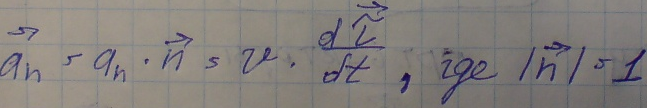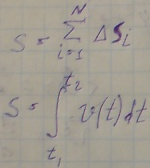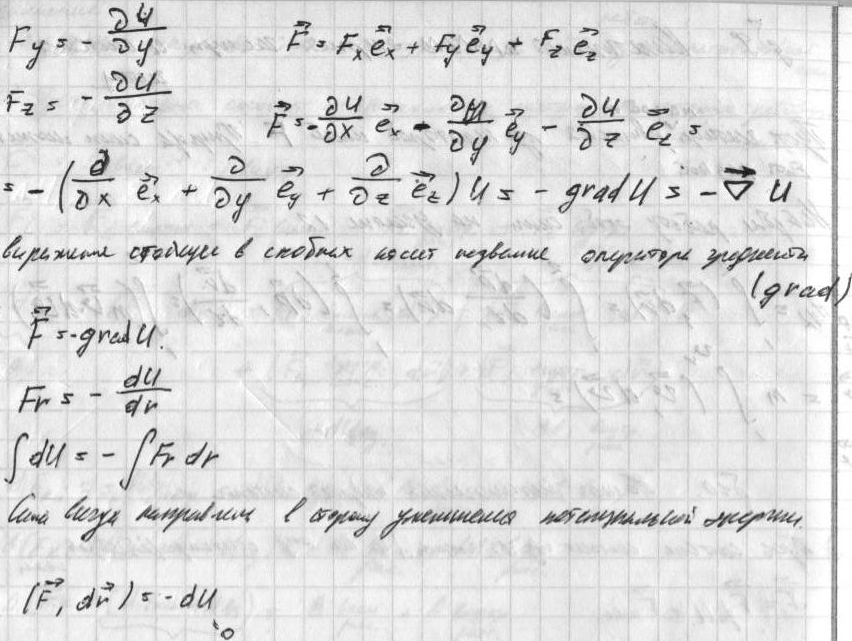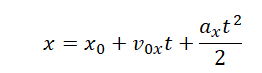Как найти уравнение движения зная ускорение

Механическое движение

О чем эта статья:

Механическое движение

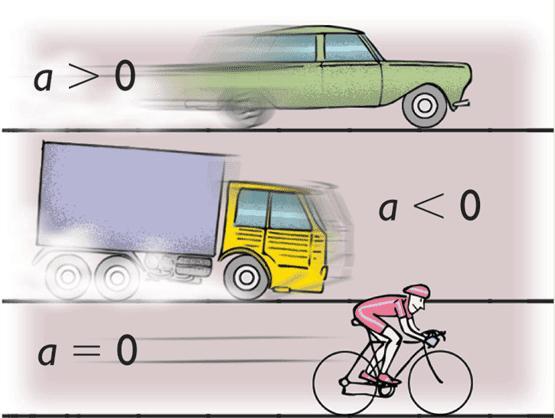
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

• тело отсчета
• система координат
• часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

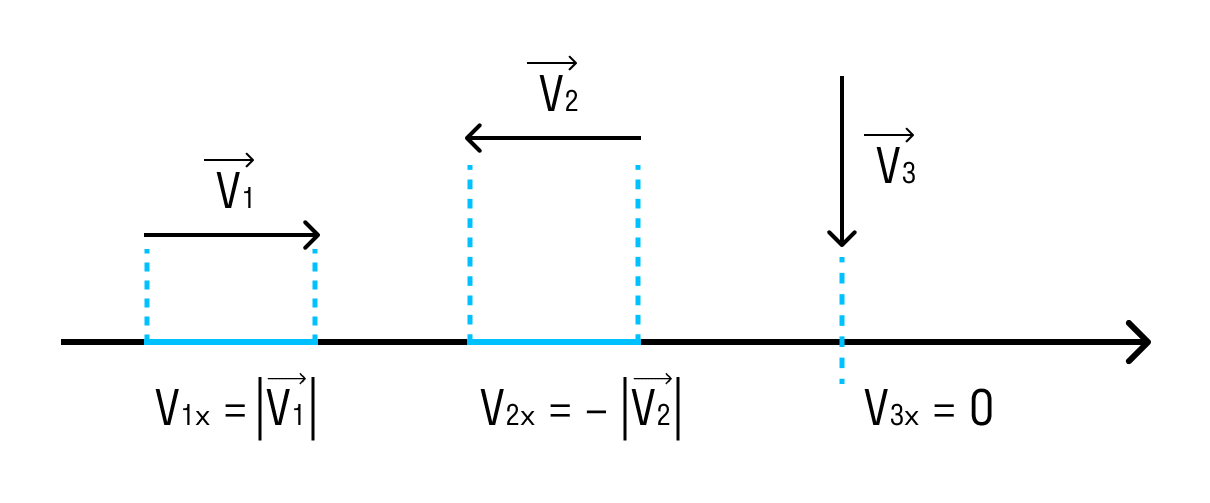
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Прямолинейное равноускоренное движение. Формулы и решение задач

Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.

Кинематические характеристики движения

Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.

Вам будет интересно: Методика ШТУР: расшифровка аббревиатуры, особенности проведения теста, итоговый анализ и результаты

В первую очередь это пройденный путь. Будем его обозначать буквой S. Согласно определению, путь — это расстояние, которое тело прошло вдоль траектории перемещения. В случае прямолинейного движения траектория представляет собой прямую линию. Соответственно, путь S — это длина прямого отрезка на этой линии. Он в системе физических единиц СИ измеряется в метрах (м).

Вам будет интересно: «Рубаха-парень»: значение в прошлом и сейчас

Скорость или как часто ее называют линейная скорость — это быстрота изменения положения тела в пространстве вдоль его траектории перемещения. Обозначим скорость буквой v. Измеряется она в метрах в секунду (м/с).

Ускорение — третья важная величина для описания прямолинейного равноускоренного движения. Она показывает, как быстро во времени изменяется скорость тела. Обозначают ускорение символом a и определяют его в метрах в квадратную секунду (м/с2).

Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.

Связь скорости и ускорения

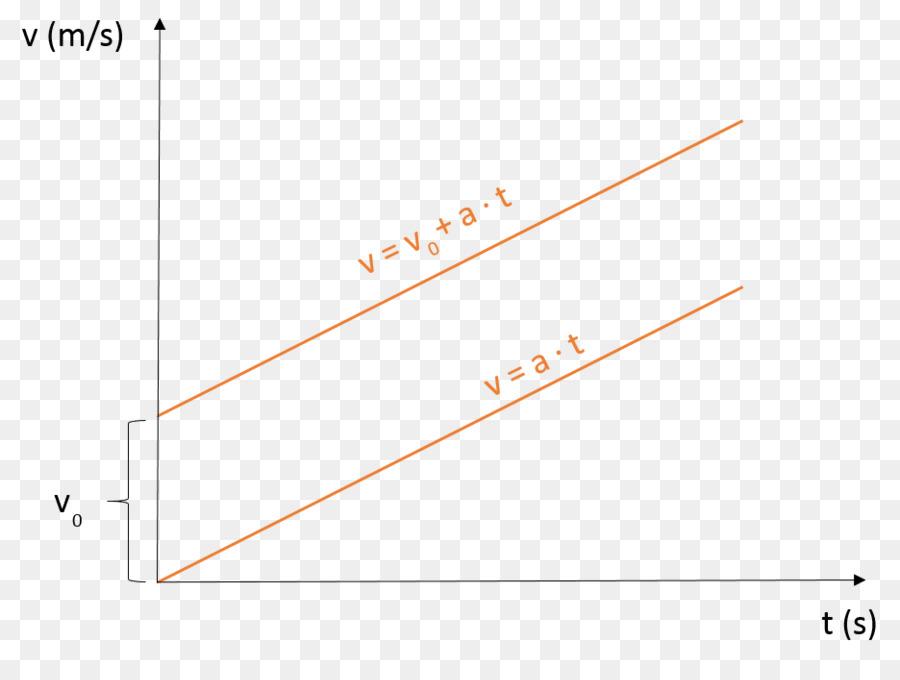
Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v0. Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:

Здесь второе слагаемое описывает прирост скорости за каждый промежуток времени. Поскольку v0 и a являются постоянными величинами, а v и t — это переменные параметры, то графиком функции v будет прямая, пересекающая ось ординат в точке (0; v0), и имеющая некоторый угол наклона к оси абсцисс (тангенс этого угла равен величине ускорения a).

На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v0, а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:

Этот вид движения называется прямолинейным равнозамедленным.

Формулы пройденного пути

На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:

S = v0 * t + a * t2 / 2.

Первый член соответствует равномерному движению без ускорения. Второй член — это вклад в пройденный путь чистого ускоренного движения.

В случае торможения движущегося объекта выражение для пути примет вид:

S = v0 * t — a * t2 / 2.

В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.

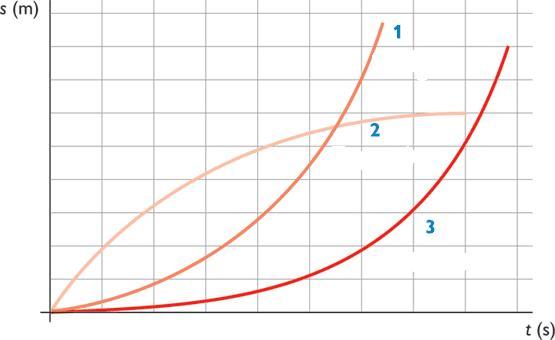
Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.

Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.

Далее в статье решим три разные задачи на использование приведенных формул.

Задача на определение времени движения

Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с2. Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?

Расстояние, которое авто за 20 секунд пройдет, будет равно:

При этом скорость, которую он наберет за 20 секунд, равна:

Тогда искомое время движения t можно вычислить по следующей формуле:

t = (S — S1) / v + t1 = (S — a * t12 / 2) / (a * t1) + t1.

Здесь S — расстояние между A и B.

Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.

Задача на расчет пути торможения

Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.

Тормозной путь S можно рассчитать по следующей формуле:

S = v0 * t — a * t2 / 2.

Время торможения t и начальную скорость v0 мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:

Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:

S = v0 * t — v0 * t / 2 = v0 * t / 2.

Подставляем значения из условия и записываем ответ: S = 145,8 метра.

Задача на определение скорости при свободном падении

Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?

Искомую скорость можно рассчитать по формуле:

Время падения тела определим из соответствующего выражения для пути S:

Подставляем время t в формулу для v, получаем:

v = g * √(2 * S / g) = √(2 * S * g).

Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.

Уравнения кинематики прямолинейного движения тела с ускорением свободного падения

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема сегодняшнего урока: «Уравнения кинематики прямолинейного движения тела с ускорением свободного падения». Мы рассмотрим методы решения задач по заданной теме и применение основных формул для движения тела с ускорением свободного падения.

Содержание:

Координатный способ определения движения точки:

При координатном способе определения движения точки должны быть даны уравнения движения, т. е. заданы координаты точки как функции времени:

Задание движения точки в прямоугольных координатах

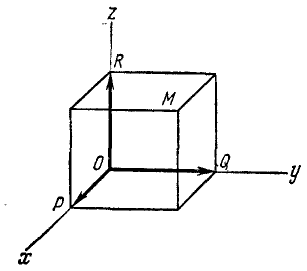
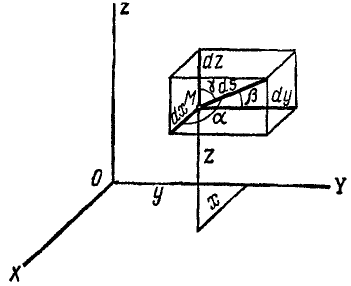
Как известно из курса аналитической геометрии, положение точки M в пространстве может быть определено положением ее проекций P, Q и R на три взаимно перпендикулярные оси (рис. 84), называемые осями координат.

Рис. 84

Положение точки P на оси Ox вполне определяют абсциссой х. Совершенно так же положение точек Q и R определяют ординатой у и аппликатой z.

Если точка M движется относительно осей xOyz, то проекции Р, Q и R перемещаются по осям и координаты точки M изменяются.

Для определения движения точки M нужно знать ее координаты для каждого мгновения, выразить их в функциях времени.

x = x(t),    (58′)
y = y(t),    (58″)
z = z(t), (58″‘)

Эти функции непрерывны, так как точка не может из одного положения перейти в другое, минуя промежуточные. Они должны быть однозначны, так как точка занимает в пространстве в каждое мгновение только одно положение.

Соотношения (58) называют кинематическими уравнениями движения точки в прямоугольных координатах, а способ определения движения точки посредством соотношений (58) называют координатным способом определения движения точки. Это название неточно, потому что, кроме прямолинейных прямоугольных координат, существует множество других координатных систем.

Если траектория точки лежит в одной плоскости, то движение точки определяют двумя уравнениями в системе координат xОy: x=x(t), y=y(t).

Следовательно, при координатном способе задания движения точки в пространстве нужно задать ее три координаты, а на плоскости—две координаты как функции времени. Если точка движется прямолинейно, то, приняв прямую, по которой она движется, за ось абсцисс, мы определим движение точки одним уравнением

x = x(t).

Если движение точки задано в координатной форме, то для определения ее траектории надо из уравнений движения исключить время

Уравнение траектории

Можно определить траекторию точки, если в уравнениях движения (58) давать аргументу t различные значения и, вычислив соответствующие значения функций, отмечать положения точки по ее координатам. Следовательно. кинематические уравнения движения точки (58) можно
рассматривать как уравнения ее траектории в параметрической форме, а время — как независимый переменный параметр.

Однако более удобно получить уравнение траектории, исключив время из уравнений (58). В самом деле, траекторией называют геометрическое место всех положений движущейся точки, но в геометрии нет понятия времени, а поэтому для получения уравнения траектории нужно из кинематических уравнений движения (58) исключить время t. Если точка движется в плоскости, то, исключив время из уравнений (58′) и (58″), мы получим соотношение, связывающее х и у:

f(x, у) = 0.    (59)

Это уравнение плоской кривой—траектории точки. Если же движение задано тремя уравнениями (58), то, исключив время, получим два уравнения между тремя координатами:
    (59^/)

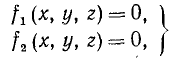
выражающие, как известно из аналитической геометрии, кривую (траекторию) в пространстве. Точнее говоря, уравнения (59) или (59′) выражают кривую, которая полностью или в некоторой своей части является геометрическим местом всех положений движущейся точки.

Иногда бывает нужно выразить в естественной форме движение точки, заданное в прямоугольных координатах уравнениями (58), и, кроме уравнения траектории, дать также уравнение (51) движения точки по траектории. Чтобы его получить, надо продифференцировать уравнения (58) и полученные дифференциалы координат точки подставить в известную из курса высшей математики формулу, выражающую абсолютную величину элемента дуги:

    (60)

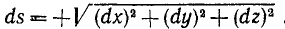
Проинтегрировав (60), мы получим уравнение (51), выражающее длину дуги s как функцию времени, или, что то же, закон движения точки по траектории.

Задача №1

По заданным уравнениям движения точки в координатной форме найти уравнение траектории и уравнение движения по траектории:

1)    х = 5 cos 2t,       y = 3+5sin 2t;
2)    x=21,2 sin² t,    у = 21,2 cos 2t.

В обоих примерах за единицу длины принят сантиметр, за единицу времени — секунда.

Решение. Чтобы определить уравнение траектории по уравнениям движения, перенесем во втором из заданных уравнений 3 влево, возведем оба уравнения в квадрат и, сложив, получим

x² + (y-3)² = 25.

Это уравнение окружности с центром в точке: x = 0, y = +3.

Чтобы получить закон движения, продифференцируем заданные уравнения: dx=—10 sin 2t dt, dy = 10 cos 2t dt.

Возводя в квадрат, складывая, извлекая квадратный корень и интегрируя, находим закон движения по траектории:
s=10t + C, где C = s₀.

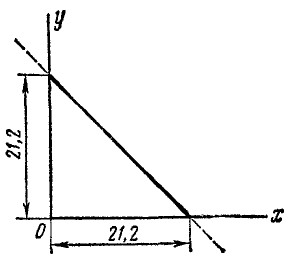
2) Исключим время из уравнений движения во втором примере:

x+y = 21,2.

Это уравнение первого порядка относительно х и у, следовательно, траектория-прямая линия. Прямая отсекает на положительных направлениях осей координат отрезки по 21,2 см. Однако не вся прямая служит траекторией точки: из заданных уравнений видно, что х и у должны быть всегда положительны и не могут быть больше 21,2 см каждый, поэтому траекторией точки является лишь отрезок прямой x+y = 21,2, лежащей в первом квадранте (рис. 85).

Рис. 85

На этом примере мы видим, что траекторией точки иногда является лишь часть линии, выражаемой уравнением траектории.

Продифференцируем уравнения движения:

dx = 21,2 ∙ 2 sin t cos t dt,
dy = 21,2 ∙ 2 sin t cos t dt.

Теперь no формуле (60) нетрудно найти элемент дуги траектории:

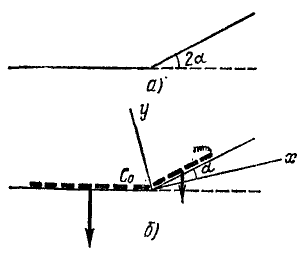
ля получения уравнения (51) движения точки по траектории остается лишь проинтегрировать найденное выражение. Интегрируем и подставляем начальные условия (при t= 0, s₀ = 0):

Ответ. Уравнения траекторий x²+(y-3)²= 25 и x+y=21,2; уравнения движения по траектории s=10t+s₀ и s = 30 sin ²t.

Задача №2

Движение точки задано уравнениями:
х = x’ cos φ (t)—y’ sin φ (t),
y = x’ sin φ (t) + y’ cos φ (t),

где х’ и у’ — некоторые постоянные величины, a φ(t)— любая функция времени. Определить траекторию точки.

Решение. Возведем каждое из уравнений в квадрат, а затем сложим их:

x² + y² = χ^‘2 + y^‘2.

По условию, х’ и у’ — постоянные. Обозначая сумму их квадратов через r², получим

x² + y² = r².

Ответ. Окружность с центром в начале координат радиуса .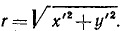

Задача №3

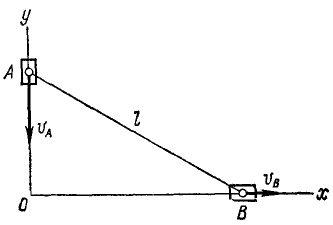
Поезд длиной l м сначала идет по горизонтальному пути (рис. 86, а), а потом поднимается в гору под углом 2α к горизонту. Считая поезд однородной лентой, найти траекторию его центра тяжести.

Рис. 86

Решение. Для решения задачи нужно определить координаты центра тяжести поезда, найти уравнения движения центра тяжести и исключить из них время.

Направим оси координат по внутренней и внешней равиоделяшнм угла 2α (рис. 86, б). Траектория центра тяжести поезда не зависит от скорости поезда. Для простоты подсчетов предположим, что он идет равномерно со скоростью υ м/сек и в начальное мгновение t=0 подошел к горе.

Тогда за время t сек на гору поднимется υt м состава поезда и останется на горизонтальном пути l — υt м. Будем считать, что единица длины поезда весит γ. 

Применяя формулы (48), найдем координаты центра тяжести поезда:

Координаты центра тяжести представлены здесь как функции времени, следовательно, полученные соотношения являются уравнениями движения центра тяжести поезда. Определяя t (или υt) из первого уравнения и подставляя во второе, найдем уравнение траектории:

Ответ. Парабола.

Задача №4

Мостовой кран движется вдоль цеха согласно уравнению х = t; по крану катится в поперечном направлении тележка согласно уравнению у = 1,5t (х и у—в м, t — в сек). Цепь укорачивается со скоростью t>=0,5. Определить траекторию центра тяжести груза (в начальном положении центр тяжести груза находился в горизонтальной плоскости хОу, ось Oz направлена вертикально вверх).

Решение. В условии задачи даны лишь два уравнения движения и вертикальная скорость груза:

откуда dz = 0,5dt, и легко получаем третье уравнение:

z = 0,5t

Определив t из первого уравнения, подставим во второе и в третье:

y= 1,5x, z = 0,5x

Координаты груза должны удовлетворять одновременно обоим уравнениям, т. е. траектория лежит одновременно в обеих плоскостях и является линией их пересечения.
Ответ. Прямая.

Алгебраическая величина скорости проекции точки на координатную ось равна первой производной от текущей координаты по времени:

Алгебраическая величина скорости проекции точки на ось

Пусть движение точки M определяется тремя уравнениями:
x =x(t),    (58′)
y = y(t),   (58″)
z = z(t).    (58″‘)

По мере движения точки M в пространстве ее проекции P, Q и R движутся по своим прямолинейным траекториям, т. е. по осям координат, и их движения вполне соответствуют движению точки М.

Так, координата (абсцисса) точки P всегда равна абсциссе точки М, а координаты точек QnR всегда равны ординате и аппликате точки М. Следовательно, при движении точки M в пространстве согласно уравнениям (58) точка P движется по оси Ox согласно уравнению (58′), а точки Q и R— соответственно по осям Oy и Oz согласно уравнениям (58″) и (58″‘).

Таким образом, движение точки M в пространстве можно разложить на три прямолинейных движения ее проекций P, Q и R.

Определим скорость υ_p точки P при движении этой точки по ее прямолинейной траектории Ох, иными словами, определим скорость проекции точки M на ось Ох.

Алгебраическая величина скорости выражается по формуле (53), причем дифференциалом расстояния точки P является дифференциал абсциссы х, а поэтому

    (61)

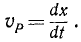
Следовательно, алгебраическая величина скорости проекции P точки M на координатную ось равна первой производной от текущей координаты х по времени t. Она положительна, если точка P движется в положительном направлении оси Ох, и отрицательна, если точка P движется в отрицательном направлении.
Аналогично получаем алгебраические скорости проекций Q и R на ось Oy и на ось Oz:

    (61″)

     (61″‘)   

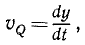
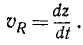
Чтобы получить векторы скоростей проекций, надо умножить величины (61) на единичные векторы:
     (61)   

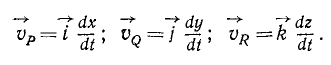
Алгебраическая величина скорости проекции точки на ось равна проекции скорости той же точки на туже ось:

Скорость проекции и проекция скорости

Пусть точка М за бесконечно малый отрезок времени dt передвинулась по своей траектории на элемент дуги ds, абсолютную величину которого выразим формулой (60):

где dx, dy и dz — проекции элемента дуги на оси координат, или, Что то же, элементарные приращения координат точки М.

На рис. 87 эти элементы условно изображены конечными отрезками. Как видно из чертежа, косинусы углов, составляемых элементарным перемещением (а следовательно, и скоростью точки), с осями х, у и z соответственно равны

     (62)   

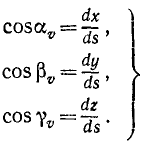
Величина скорости точки M может быть определена по (53):

Чтобы определить проекцию скорости на какую-либо ось, надо умножить абсолютную величину скорости на косинус угла между  направлением скорости и направлением этой оси. Таким образом, для проекций скорости точки M на оси координат имеем:

   (63′)

   (63″)

    (63″‘)

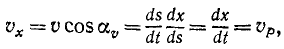
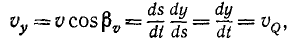
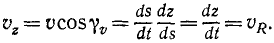
Рис. 87

Равенства (63) словами нужно читать так: проекция скорости точки на ось равна алгебраической скорости проекции точки на ту же ось.

Задача №5

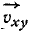
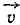
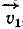
Доказать, что проекция скорости точки M (х, у, z) иа плоскость хОу равняется скорости , с которой движется по плоскости проекция M₁ (х, у, О) точки M на ту же плоскость.

Решение. Скорость 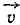точки M составляет с осью Oz угол γ_υ, следовательно, угол, составляемый ею с плоскостью хОу, равен 90° — yυ п косинус этого угла равен sinγ_υ. Поэтому модуль проекции скорости точки M на плоскость хОу

Подводя 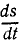под радикал и выражая cosγ_υ, по формуле (62), мы убедимся, что проекция скорости на плоскость равна по величине скорости проекции:

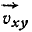
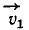
Направления векторов и тоже совпадают, так как направляющие косинусы их одинаковы. Теорема доказана.

Модуль скорости точки равен квадратному корню из суммы квадратов проекций скорости на оси координат:

Модуль скорости. Возведем в квадрат каждое из равенств:
   (63)

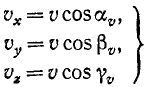
и сложим их:

Сумма квадратов направляющих косинусов равна единице и

или

   (64)

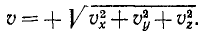
Перед радикалом взят положительный знак, так как величина скорости (ее модуль) всегда положительна. В этом ее существенное отличие от алгебраической величины скорости (53), характеризующей скорость точки при движении по заданной траектории и имеющей знак « + » или «—» в зависимости от направления движения. Величину (64) иногда называют полной скоростью.

Направление скорости можно определить по направляющим косинусам скорости:
 

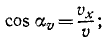
Направляющие косинусы скорости

Равенство (64) позволяет определить модуль скорости точки, движение которой задано уравнениями (58). Направление скорости определяется по косинусам углов, составляемых положительными направлениями осей координат с направлением скорости. Значения этих косинусов, называемых направляющими косинусами скорости, мы получим из уравнений (63):

   (62′)

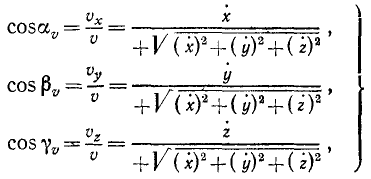
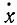
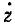
где , и — производные от х, у и z по t.

Если точка движется в плоскости хОу, то γ_υ = 90^o, cosγ_υ = 0 и cos α_υ = sin β_υ.

Задача №6

Уравнения движения суть

 

Определить траекторию и скорость.

Решение. Из уравнений движения следует, что х и у всегда больше нуля.
Для определения уравнения траектории возведем каждое из уравнений движения в квадрат и составим разность

x² — у² = a²

Для определения скорости найдем сначала ее проекции:

а затем уже и полную скорость.

Ответ. Траектория — ветвь гиперболы x² — у² = a² — расположена в области положительных значений х; скорость .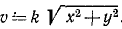

Задача №7

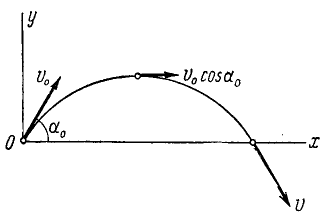
Движение точки задано уравнениями

причем ось Ox горизонтальна, ось Oy направлена по вертикали вверх, υ₀, g и 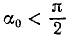—величины постоянные. Найти траекторию точки, координаты наивысшего ее положения, проекции скорости на координатные оси в тот момент, когда точка находится на оси Ох.

Решение. Уравнения описывают движение тела, брошенного со скоростью υ₀ под углом α₀ к горизонту (к оси Ох).
Чтобы найти уравнение траектории, определим время из первого уравнения и подставим найденное значение во второе; получим

уравнение параболы, проходящей через начало координат (рис. 88).

Рис. 88

Чтобы определить координаты наивысшего положения, мы можем применить известные из дифференциального исчисления правила нахождения максимума функции, т. е. взять производную , приравняв ее нулю, определить значение х и, подставив его в уравнение траектории, определить соответствующее значение у, убедившись при этом, что вторая производная . Однако мы найдем координаты наивысшего положения точки другим методом, для чего, продифференцировав по времени уравнения движения точки, найдем проекции ее скорости:

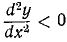
Первое из этих уравнений показывает, что проекция скорости на горизонтальную ось постоянна и равна проекции начальной скорости.

Исследование второго уравнения убеждает, что проекция скорости на вертикальную ось в начальное мгновение положительна и равна υ₀ sin α₀; затем, по мере увеличения t, проекция υ_y уменьшается, оставаясь положительной до мгновения 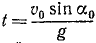, когда υ_y обращается в нуль, после чего υ_y становится отрицательной, возрастая по абсолютной величине с течением времени t.

Таким образом, точка движется вправо, сначала поднимаясь, затем опускаясь. Мгновение , при котором точка кончила подниматься, но еще не начала опускаться, соответствует максимальному подъему точки. В это мгновение скорость горизонтальна и . Подставляя найденное значение t в уравнения движения, найдем координаты наивысшей точки траектории:

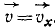
Определим проекции скорости в мгновение, когда точка находится на оси Ох. В это мгновение ордината точки равна нулю. Приравняем пулю второе из уравнений движения:

Точка находится на оси Ox два раза: при t=0 при 

Первое значение t соответствует началу движения, второе —падению точки на ось Ох. Второе значение равно времени всего полета, и оно вдвое больше полученного нами ранее времени наивысшего подъема: время падения равно времени подъема.

Подставляя значение t=0 в уравнения, определяющие проекции скорости, найдем проекции скорости в начальное мгновение:

υ_x = + υ₀ cos α₀, υ_y = + υ₀ sin α₀.

Подставляя второе из найденных значений t, найдем скорости в момент падения:

υ_x = + υ₀ cos α₀, υ_y = — υ₀ sin α₀.

Ответ: 1) Парабола 

2) 

3) υ_x = υ₀ cos α₀, υ_y = 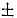υ₀ sin α₀.

причем верхний знак соответствует началу движения, а нижний—концу.

Задача №8

По осям координат (рис. 89) скользят две муфты A и B, соединенные стержнем AB длиной l. Скорость В равна υ_B.

При каком положении муфт скорость муфты А вдвое больше υ_B?

Рис. 89

Решение. Координата точки А связана с координатой точки В соотношением

Считая х и у функциями времени и продифференцировав это равенство по времени, найдем зависимость между скоростями обеих точек:

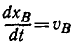
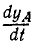
Но и по условию надо, чтобы величина  была равна 2υ_B, т. е.

откуда после алгебраических преобразований получаем ответ.

Ответ: 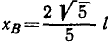 (см. задачи № 57 и 89, где даны другие решения).

Проекция ускорения точки на координатную ось равна первой производной по времени от проекции скорости на ту же ось или второй производной от текущей координаты по времени:

Ускорение проекции и проекция ускорения

Ускорение характеризует изменение скорости точки в данное мгновение. Оно выражается пределом отношения изменения вектора скорости к соответствующему промежутку времени при стремлении этого промежутка времени к нулю.

Для того чтобы определить ускорение точки M при ее движении в пространстве, рассмотрим сначала движение по оси Ox точки Р, являющейся проекцией точки M на эту ось.

Пусть в некоторое мгновение t алгебраическая величина скорости точки P была υ_х, а в мгновение t_l = t + Δt стала υ_x+∆υ_x. Тогда ускорение точки P по величине и по знаку выразится пределом

Если знаки υ_x и a_p одинаковы, то движение точки P ускоренное, а если различны, то замедленное.

Аналогично выразятся ускорения проекций Q и R точки M на другие координатные оси:

Проекции υ_x, υ_y и υ_z сами являются производными по времени от координат точки, поэтому ускорения проекций можно выразить вторыми производными по времени от координат точки. Эти равенства характеризуют не только величины, но и знаки ускорений проекций. Иными словами, они выражают изменение алгебраических скоростей проекций P, Q и R в мгновение t.

Только что доказанная теорема о равенстве алгебраической скорости проекции точки на ось и проекции скорости той же точки на ту же ось справедлива для любого момента времени. Следовательно, эта теорема относится не только к скорости, но и к ее изменению в любое мгновение, т. е. к ускорению. Это значит, что написанные выше равенства выражают также проекции a_x, а_у и а_z ускорения а точки M на оси координат O_x, O_y и O_z:

   (65)

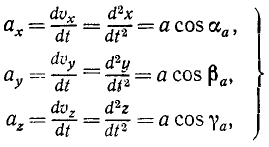
где cosα_a, cosβ_a и cosγ_a—направляющие косинусы ускорения.

Можно рассматривать эти величины (65) как векторы, направленные по осям координат:

   (65′)

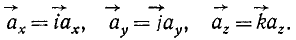
Модуль ускорения точки равен квадратному корню из суммы квадратов проекций ускорения на оси координат:

Величина ускорения при координатном способе задания движения точки

Возведем в квадрат каждое из равенств:

и затем сложим их:

откуда 

   (66)

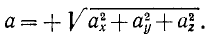
Перед радикалом взят знак плюс, так как модуль вектора—величина положительная. Ускорение точки в отличие от проекций ускорения на оси координат или на другие направления обычно называют полным ускорением. Поэтому равенство (66) можно прочитать так: величина полного ускорения точки равна квадратному корню из суммы квадратов его проекций на оси координат.

Направление ускорения можно определить по направляющим косинусам ускорения:
, 

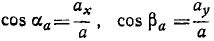
Направляющие косинусы ускорения

Направление ускорения определяют по косинусам углов, составляемых положительными направлениями осей координат с вектором ускорения. Формулы направляющих косинусов получаем из уравнений (65):
   (67′)

   (67»)

   (67»’)

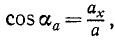
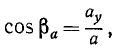
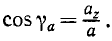
Для определения направления ускорения в каждом конкретном случае надо сначала найти ускорение проекций по (65), для чего необходимо дважды продифференцировать уравнения движения (58), затем найти величину ускорения по (66), а потом определить направляющие косинусы ускорения по (67).

Направление ускорения обычно не совпадает с направлением скорости, и направляющие косинусы (67) ускорения только при прямолинейном ускоренном движении точки постоянно равны направляющим косинусам (62) скорости.

Если точка движется в плоскости хОу, то γ_a = 90^o, cosγ_a = 0, cosα₀ = sin βa.

Задача №9

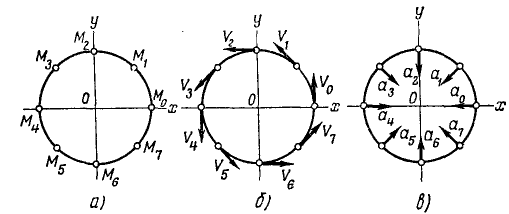
Точка M движется в системе координат хОу согласно уравнениям х= r cos πt, y=r sinπt, где х и у—в см, a t — в сек. Найти уравнение траектории точки М, ее скорость, направляющие косинусы скорости, ускорение, направляющие косинусы ускорения. Для значений времени t=0; 0,25; 0,5; 0,75, …. 2 сек дать чертежи положений точки M, вектора скорости и вектора ускорения.

Решение. Из уравнения движения видно, что координаты точки M являются проекциями на соответствующие оси радиуса-вектора r, составляющего с осью абсцисс угол πt:

Для определения траектории точки исключаем время из уравнений движения. Получаем уравнение окружности

x² + y² = r²

Найдем теперь проекции скорости на оси координат, для чего продифференцируем по времени уравнения движения:

откуда по (64) получаем модуль скорости

Величина скорости точки M постоянна.

Направляющие косинусы скорости определим по формуле (62′):

Эти соотношения показывают, что направление скорости непрерывно меняется и что скорость перпендикулярна радиусу-вектору, проведенному из центра О в точку М.

Ускорение точки M найдем по его проекциям, для чего продифференцируем выражения, полученные для проекций скорости:

откуда по (66) получаем величину ускорения

Ускорение характеризует быстроту изменения вектора скорости не только по величине, но и по направлению, поэтому, несмотря на постоянство модуля скорости точки М, ускорение этой точки не равно нулю. Как видно из полученного

Рис. 90

равенства, величина полного ускорения постоянна. Направление ускорения определим по направляющим косинусам согласно (67):

Направление ускорения точки M противоположно направлению радиуса-вектора.
Положения точки M в различные мгновения показаны на рис. 90, а, векторы скорости — на рис. 90,6 и векторы ускорения — на рис. 90, в.

Ответ. Точка M движется по окружности радиуса r против часовой стрелки с постоянной по величине скоростью υ = rπ и с постоянным по величине ускорением a = rπ².

Задача №10

Снаряд выбрасывается из орудия с начальной скоростью υ=1600 м/сек под утлом α₀ = 55^o к горизонту. Определить теоретическую дальность и высоту обстрела, учитывая, что ускорение свободно падающих тел g = 9,81 м/сек².

Решение. Сначала составим уравнения движения снаряда в координатной форме, направив оси, как показано на чертеже (см. рис. 88), для этого определим проекции ускорения:

Разделив переменные, интегрируем:
υ_х= С₁, υ_y = — gt + С2

Подставляя вместо переменных величин их начальные значения, увидим, что C₁ и C₂ равны проекциям начальной скорости:

1600 cos 55^o = C_1, 1600 sin 55^o = — gt + C_2.

Подставим их в уравнения, полученные для проекций скорости:

Разделяя переменные и интегрируя, найдем

При t = 0 координаты снаряда были: х =0, у = 0. Подставляя эти данные, найдем, что C₃ = O и C₄ = O. Значения cos 55° и sin 55° найдем в тригонометрических таблицах. Уравнения движения снаряда примут вид:

Далее поступим, как при решении задачи № 42: приравняв вертикальную скорость нулю, найдем время подъема снаряда (t= 133,7 сек); подставляя это значение t в уравнение движения по оси Оу, найдем теоретическую высоту обстрела (h = 87 636 м); удваивая время /, найдем время полета снаряда (t = 267,4 сек); подставляя это значение- в уравнение движения по оси Ох, найдем теоретическую дальность обстрела (l = 245 393 м).
Ответ. l = 245 км; h = 87,5κм.

Уравнение
движения

Уравнение
движения можно записать 3-мя способами:

1)Векторный
способ

При
перемещении точки изменяются, как по
величине, так и по направлению.

2)Координатный
способ

Декартова
система координат x
_|_ y _|_ z

Любой
вектор можно представить как его модуль
умноженный на его ортвектор.

3)Параметрический
способ

Если
заранее известна траектория по которой
движется точка.

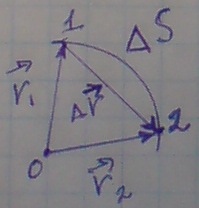
Перемещение

Пусть
точка А движется и за времяtиз положения 1 в положение 2.

Перемещение-
это векторная физическая величина,
которая характеризует перемещение
точки из начального положения в конечное.

Путь-это(величина
скалярная) расстояния, которое проходит
точка по траектории.

Скорость

Пусть
точка движется по некоторой траектории,
при этом она движется либо быстрее, либо
медленнее.

Скорость-это
векторная физическая величина, которая
характеризует перемещение точки.

1)Векторный
способ

Средний
вектор скорости

Модуль
вектора скорости

Средняя
скорость

Модуль
скорости

2)Координатный
способ

3)Параметрический
способ

Скорость
всегда направлена по касательной к
траектории.

Касательная
траектории – это

Ускорение

Ускорение
– это векторная физическая величина,
которая характеризует скорость
перемещения тела.

1)Векторный
способ

2)Координатный
способ

3)Параметрический
способ

(это
тангенциальное и нормальное
ускорение(следующий вопрос))

2. Нормальное и тангенциальное
ускорение и радиус кривизны.

Тангенциальное
ускорение – отвечает за изменение
величины скорости по траектории.

Нормальное
ускорение – характеризует изменение
направления скорости в пространстве и

при
движении точки по траектории может
изменить её модуль и ускорение.

R(в
формулах)- это радиус кривизны.

3. Формула пути для движения
с переменной скоростью. Средняя скорость…

Средняя
скорость

Средняя
скорость – это скорость, с которой точка
проходит тот же путь, за то же время,
двигаясь равномерно.

— среднее
значение модуля скорости

4,Вращательное движение.
Векторы углового перемещения, угловой
скорости, углового ускорения.

Движение,
траекторией которого является окружность,
называется – вращательным движением.

Вращательное
движение – это частный случай
криволинейного движения.

Если
точка движения на окружности, то её
движение удобно высчитывать не с помощью
линейных, а с помощью угловых коэффициентов.

Если
точка вращается по окружности равномерно,
т.е. с постоянной скоростью, то ωимеет название – круговой частоты.

T– это время, за которое частица совершает
1 оборот, вращаясь с постоянной скоростью.

Мы не учитываем в предыдущем параграфе,
что при движении точки на окружности:

а) может
изменяться положение, плоскости в
пространстве.

б) точка
может двигаться, как по часовой, так и
против часовой.

Учтём
эти обстоятельства, для этого рассмотрим
рисунок.

В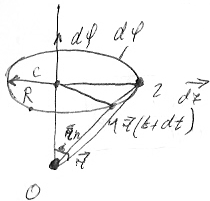екторdφ
характеризует угловое перемещение
точки, направлен по оси и его направление
определяется по правилу правого винта.

Вектор,
определённый таким образом называется
псевдовектором или аксиальным вектором.

Поворот тела на некоторый угол φ (угловое
перемещение) можно задать в виде отрезка,
длина которого равна абсолютной
величине φ (в радианах), а направление
совпадает с осью вращения. Обычно это
направление связывают с правилом правого
винта (рис. 2.4).

Рис. 2.4

Таким образом, повороту (угловому
перемещению) j можно задать численное
значение и направление.

Однако этого еще недостаточно, чтобы
угловое перемещение считать вектором.
Необходимо, чтобы изображаемые таким
образом повороты складывались по правилу
сложения векторов, т.е. геометрически,
что характерно для точных векторов.

Если поворот dφ бесконечно мал
(dφ << 2π), то операция геометрического
сложения угловых перемещений выполняется.

Следовательно, малые повороты (угловые
перемещения) можно рассматривать как
векторы  , у которых абсолютное
значение равно углу поворота в радианах.

Векторы типа ,
направление которых связывается с
направлением оси вращения,
называют аксиальными или псевдовекторами,
в отличие от векторов,
которые называют полярными. Их направление
вытекает естественным образом из природы
самих величин.

Угловая
скорость — векторная физическая
величина, характеризующая скорость
вращения тела. Вектор угловой скорости
по величине равен углу поворота
тела в единицу времени:

,

Угловое
перемещение:

Обозначение	Описание
	Время, размерность в СИ — с
	Угловая скорость (начальная), размерность в СИ — рад с
	Угловое ускорение, размерность в СИ — рад с2
	Угол, размерность в СИ — рад
	Угол (начальный), размерность в СИ — рад

5, Законы Ньютона и их
физическое содержание. Масса, сила,
импульс. Закон сохранения импульса.

Динамика-это
раздел механики, который изучает движение
тел под действием приложенных к ним
сил.

В основе
динамики лежат 3 закона Ньютона.

Первый
закон Ньютона.

Всякое
тело сохраняет состояние покоя или
прямолинейного равномерного движения
до тех пор, пока действие на него со
стороны других тел не изменит его
состояние.

Инертность
– это способность тела сохранять своё
состояние.

Инерциальные
системы отсчёта – это такие системы
отсчёта, в которых выполняется первый
закон Ньютона, т.е. это такие системы
отсчёта, в которых тело либо покоится,
либо движется равномерно и прямолинейно.

Физический
закон первого закона Ньютона заключается
в том, что он утверждает, что инерциальные
системы отчёта существуют.

А)Масса – мера инертности тела, т.е. она
характеризует степень неподатливости
тела к изменению её скорости.

Масса
величина скалярная и в системе Си
измеряется в кг.

Масса
есть величина постоянная и не изменяется
в процессе движения с течением времени.

Масса
величина аддитивная. Если масса состоит
из отдельных частей, то общая масса
равна сумме масс отдельных её частей.

Б)Импульс тела – это векторная величина,
которая численно равна произведению
массы тела на её скорость.

Если
механическая система состоит не из
одной части, а из нескольких частиц, или
тел, то вектор импульса будет равен
сумме импульсов этих тел.

В)Сила – характеризует меру воздействия
на данное тело со стороны других тел
или полей.

Сила
векторная величина. Если на тело действует
несколько сил, то результирующая сила,
будет равна геометрической сумме всех
действующих сил на тело.

Если
размерами тела можно пренебречь в
условии данной задачи, то точку приложения
всех сил на тело можно сместить в центр
масс.

Если
размерами тела нельзя пренебречь, то
всегда надо смотреть точку приложения
всех

сил и
если она создаёт вращение тела, то её
нельзя переносить.

Существует
4 вида фундаментального взаимодействия:

-гравитационное
– между массами тел

-электромагнитное
– взаимодействие обуславливаются
наличием заряда у тел и движением этих
тел

-сильное(ядерная
сила) действует на расстоянии 10 ^-15
метра

-слабое
(ответственная за распределение элем.
часть) проявляется на расст. 10 ^-17 метра

Слабые
и сильные –это коротко действующие
силы (на малых расстояниях)

Все
остальные силы не являются
фундаментальными(сила трения, упругости
и т.д.)

Все
силы подразделяются на:

1. Консервативные
   – это такие силы, работа которых не
   зависит от формы пути и определяются
   лишь начальным и конечным положением
   частицы(отн: гравитационные, кулоновские,
   сила упругости, тяжести)

2. Сторонние
   силы: диссипативные, гироскопические.

Диссипативные — это силы, действия
которых приводят к потере энергии
системы.(Сила трения, сопротивления)

Гироскопические – это силы, которые
всегда зависят от скорости, не совершают
работы и направлены перпендикулярно к
скорости частиц.(Сила Лоренса, Кориолиса)

Второй
закон Ньютона.

Ускорение
тела, в инерциальной системе отсчёта,
прямопропорционально действующей силе
и обратнопропорционально массе.

Физический
смысл этого закона заключается в том,
что он является уравнением движения.

Замечание:
Два закона существенно отличаются друг
от друга.

Третий
закон Ньютона.

Сила с
которой действуют друг на друга
взаимодействующие тела, равна по величине
и противоположна по направлению, причём
они не уравновешивают друг друга, т.к.
не приложены к одному и тому же телу, а
к разным.

Физический
смысл этого закона заключается в том,
что по изменению состояния одного из
взаимодействующих тел, можно определить
состояние второго.

Замечание:

Когда
Ньютон формулировал свои законы, он
думал, что взаимодействие распространяется
мгновенно. Однако по истечению некоторого
времени выяснили, что взаимодействие
распространяется со скоростью не
превышающую скорость света. Поэтому
законы Ньютона применяются только в
классической физике.

Закон сохранения импульса.

Закон
сохранения импульса – это фундаментальный
закон природы, который следует из
однородности пространства. Однородность
пространства означает, что если система,
как целое, взять и перенести из одной
точки пространства в другую, то все
процедуры будут проходить в ней точно
так же, как и в предыдущей точке. Получим
этот закон из основного уравнения
динамики.

6. Работа и мощность.

Работа
– это величина скалярная. Зависит от
величины силы начального перемещения.
Т.к. cosзнакопеременная
величина, то А может быть =,>,< 0. Если
сила перпендикулярно направлена
перемещению, то работа = 0. В системе СИ
работа измеряется в Джоулях [А]=H*M=Дж.

Работа
величина аддитивная.

Мощность
– это физическая величина, которая
характеризует интенсивность совершения
работы, т.е. работа, совершённая в единицу
времени

Мощность
в системе СИ измеряется в Вт.

7. Силовое поле. Консервативные
силы. Диссипативные силы. Гироскопические
силы. Потенциальная энергия. Связь между
потенциальной энергией и консервативной
силой.

Силовым
полем называется область в пространстве,
в каждой точке которого, на помещенную
туда частицу действует сила, закономерно
изменяющаяся от точки к точке.

Т.о.
характер силового поля определяется
характером сил действующих в этом поле.

Если
на частицу действуют силы направленные
к одному и тому же центру и величина
зависит от расстояния от этой точки до
силового центра, то такие силы называются
центральными и само поле называется
центральным.

Если
силы в некотором силовом поле на частицу
действуют всё время одинаковые по
величине и направлению, то такое поле
называется однородным.

Если
силы действуют на частицу, не изменяясь,
в течение определ. времени, то такое
поле называется стационарным.

Если
величина и направление действующих сил
изменяется в течении времени, то такое
поле нестационарное т.е. зависит от
времени.

Стационарное
силовое поле, в котором работа по
перемещению частицы из точки 1 в точку
2 не зависит от формы пути, а определяется
лишь начальным и конечным положением
частицы называется потенциальным, а
силы, которые действуют в этом потенциальном
поле, называются консервативными.

Чтобы
определить является ли эта сила
консервативной, а поле потенциальным,
необходимо сосчитать работу этой силы
по перемещению частицы из точки 1, в
точку 2.

И если
работа не зависит от формы пути, а
определяется лишь начальным и конечным
положением частицы, то тогда эта сила
является консервативной, а поле, в
котором они действуют потенциальным.

Работа
в потенциальном поле по замкнутому
контуру равна 0.

Неконсервативные
силы подразделяются на: диссипативные
и гироскопические.

Диссипативные
силы – это силы, которые приводят к
рассеиванию энергии, т.е. уменьшению
энергии системы (силы трения, силы
вязкости).

Диссипативные
силы – это силы, полная работа которых
всегда отрицательна. Такие силы всегда
зависят от скорости (пропорциональны
скорости) и направлены всегда в сторону
противоположную скорости.

Гироскопические
силы – это силы, которые всегда зависят
от скорости и направлены перпендикулярно
к скорости работы этих сил, всегда равны
0 (в том числе и по замкнутому контуру).
От консервативных сил отличаются тем,
что определяются не только положительными
частицами, но и скоростью (сила Лоренса
и сила Ньютона)

Потенциальная энергия
частицы.

Пусть
имеется потенциальное поле, то работа
по перемещению этой частицы из точек в
точку О будет функцией радиуса вектора
определяющее положение этих точек.

Эту
функцию называют потенциальной энергией
частицы. Потенциальная энергия – функция
состояния частицы. Потенциальная энергия
является скалярной функцией.

Таким
образом мы показали, что работа в
потенциальном поле равна убыли
потенциальной энергии частицы в этом
поле.

Потенциальная энергия
системы частиц (невзаимодействующая и
взаимодействующая).

1) Пусть
эта система находится во внешнем
потенциальном поле.

2)Потенциальная
энергия системы взаимодействующих
частиц, они взаимодействуют, но находятся
во внешнем потенциальном поле.

Если
имеется система взаимодействия частиц,
то система обладает собственной
потенциальной энергией взаимодействия,
которая определяется взаимным
расположением этих частиц.

Если
происходит изменение конфигурации
системы, то работа всех внутренних
центральных сил равна убыли собственной
потенциальной энергии системы.

Если
при движении системы её конфигурация
не изменяется, то энергия (внутренняя)
не изменяется и внутренние силы работы
не совершают.

3)Система
взаимодействия частиц находящихся во
внешнем силовом поле.

не является аддитивной.

Связь
между потенциальной энергией и
консервативной силой.

Определение и формулы

Уравнение координаты — зависимость координаты тела от времени:

x = x(t)

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с². Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с² без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с² и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с², достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Алиса Никитина | Просмотров: 14.8k