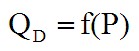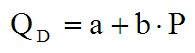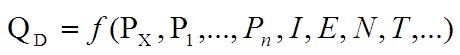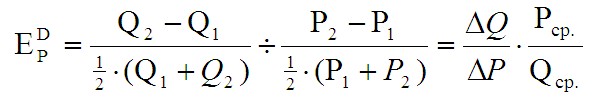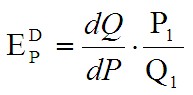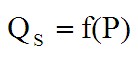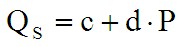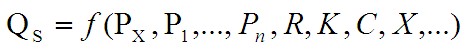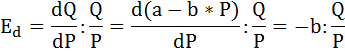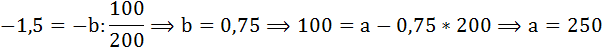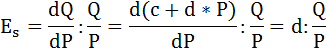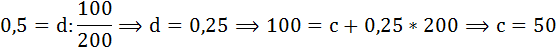Как найти уравнение функции рыночного спроса - Исправление недочетов и поиск решений вместе с Examum.ru

5.3. От индивидуального спроса к рыночному спросу

Мы вывели
кривую индивидуального спроса и
объяснили с помощью эффектов дохода и замещения её отрицательный наклон. Но в
большинстве исследований используется кривая рыночного спроса.

Мы видели также как поведение
отдельного потребителя определяет кривую спроса, то есть связь между ценой, по
которой он мог бы купить товар, и количеством, которое он решает купить. На
большинстве рынков все потребители покупают товар по одной цене, поэтому можно
говорить о единой рыночной цене и единой кривой спроса, представляющей общий
спрос всех потребителей на данный товар как функцию его цены. Так как общее
количество, на которое предъявляется спрос при любом уровне цены это количество
которое хочет купить первый потребитель по данной цене плюс количество, которое
хочет купить второй потребитель по данной цене плюс … то кривая рыночного спроса представляет
собой горизонтальную сумму всех индивидуальных кривых спроса, как показано
на рис. 5-6.

Предположим на рынке действуют три покупателя,
спрос каждого из которых представлен на
графике линейной кривой спроса d₁, d₂ и d₃.

Покажем сначала, как
можно сложить кривые индивидуального спроса геометрически. Затем рассмотрим
алгебраическое решение задачи.

Поскольку все
функции индивидуального спроса линейны, постольку сложение их даёт тоже
линейную функцию рыночного спроса. Но полученная линия будет ломаной, состоящей
из нескольких отрезков, каждый из которых
соответствует определённому диапазону изменения цены. Найдём критические
точки, соединив которые мы получим эту ломаную кривую.

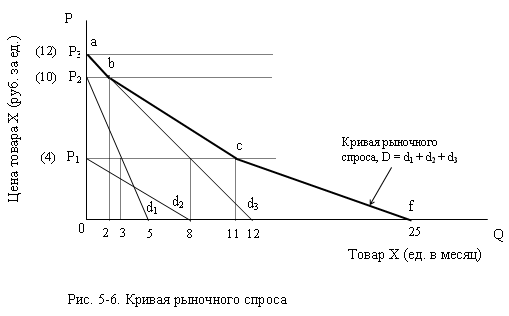
При рыночной цене Р₃ величина спроса на рынке равна 0, так как ни один из
потребителей не готов покупать по этой цене даже единицу товара Х (D = d₁+d₂+d₃= 0+0+0 = 0). Мы получили первую точку на кривой
рыночного спроса, а с координатами (0,Р₃).

В диапазоне цены между Р₃ и Р₂ единственным покупателем товара является 3-й
потребитель. Рыночный спрос при цене Р₂ равен: D = d₁+d₂+d₃= 0+0+2 = 3. Координаты второй точки кривой
рыночного спроса, b – (2,P₂). Поэтому в этом ценовом
диапазоне рыночная кривая спроса совпадает с d₃ на участке ab.

В ценовом диапазоне Р₂ – Р₁ спрос
предъявят 1-й и 3-й потребители. При цене Р₁
величина рыночного спроса составит D = d₁+d₂+d₃= 3+0+8 = 11.
Координаты с — следующей точки кривой
рыночного спроса – (11,Р₁).
Соединив прямой линией точки b и c, получим участок кривой рыночного
спроса bc.

Наконец,
при Р=0 все три потребителя предъявят спрос: D = d₁+d₂+d₃= 5+8+12=25. Соединив прямой линией точку f (25,0) с точкой с,
получим последний участок кривой рыночного спроса сf.

Как
получить уравнение функции рыночного спроса, если известны уравнения функций индивидуального спроса?

Изображённые
на рис. 5-6 функции индивидуального спроса, описываются уравнениями:

Спрос
1-го потребителя: Q₁ = 5 – 0,5P;
(1)

Спрос
2-го потребителя: Q₂ = 8 – 2P; (2)

Спрос
3-го потребителя: Q₃= 12 – P
(3)

Для того, чтобы
определить какой будет величина совокупного спроса при любом уровне цены на
рынке, нужно алгебраически сложить уравнения индивидуального спроса: Q^d_рын. = Q₁+ Q₂ +Q₃.

Однако простое
решение: Q^d_рын = 25 – 3,5Р, было бы ошибочным, поскольку оно не учитывает того, что в
некоторых ценовых диапазонах рыночный спрос состоит из спроса не всех, а только
отдельных потребителей. Поэтому при суммировании приходится эти диапазоны
учитывать. Определим их.

Из уравнения (3)
найдем, что при Р ≥ 12 спрос 3-го потребителя будет равен нулю (на рис. 5-6 Р₃=12). Из уравнения (2)
следует, что если Р≥ 10, то спрос 2-го потребителя равен 0 ( на рис. 5-6 этому
уровню цены соответствует Р₂.
Из уравнения (1) находим, что при Р≥ 4 спрос 1-го потребителя тоже равен 0.

Следовательно, если
10 ≤
Р
≤ 12, то рыночный спрос состоит
только из спроса 3-го потребителя. В этом ценовом диапазоне уравнение функции
рыночного спроса представлено только
уравнением (3): Q^d_рын =Q₃= 12 – P.

В диапазоне 4 ≤ Р ≤ 10 спрос на рынке предъявляют 3-й и 1-й потребители. Поэтому на этом
участке рыночный спрос: Q^d_рын. = Q₁+ Q₃ = (5 –
0,5Р) + (12 – Р) = 17 – 1,5Р.

Наконец, если 0 ≤ Р ≤ 4, то Q^d_рын. = Q₁+ Q₂ +Q₃ = (5 – 0,5Р) + (8 –
2Р) + (12 – Р) = 25 –3,5Р.

Понятно, что кривая рыночного спроса, являясь
горизонтальной суммой нисходящих индивидуальных кривых спроса, также имеет
отрицательный наклон. Даже, если некоторые потребители имеют восходящую кривую
спроса, то они не делают погоды на данном рынке, так как подавляющее
большинство покупателей имеют нормальные, нисходящие кривые спроса. Это ещё
одна причина, по которой мы можем не беспокоиться о товаре Гиффена в дальнейшем
анализе.

Есть несколько
интересных случаев, когда рыночный спрос
формируется не как простая сумма спроса отдельных покупателей. Эти случаи – так
называемый «эффект повального увлечения» (bandwagon effect), «эффект сноба» и «эффект Веблена».

Источник

Спрос и предложение

Сегодня практически любой развитой стране мира свойственна рыночная экономика, при которой вмешательство государства минимально или вовсе отсутствует. Цены на товары, их ассортимент, объемы производства и продажи — все это складывается стихийно в результате работы рыночных механизмов, важнейшие из которых это закон спроса и предложения. Поэтому рассмотрим хотя бы сжато основные понятия экономической теории в этой области: спрос и предложение, их эластичность, кривая спроса и кривая предложения, а также факторы их определяющие, рыночное равновесие.

Спрос: понятие, функция, график

Очень часто приходится слышать (видеть), что такие понятия как спрос и величина спроса смешивают, считая их синонимами. Это неправильно — спрос и его величина (объем) совершенно разные понятия! Рассмотрим их по отдельности.

Спрос (англ. «Demand») — платежеспособная потребность покупателей в определенном товаре при определенном уровне цен на него.

Величина спроса (объем спроса) — количество товаров, которое покупатели желают и могут приобрести по данной цене.

Итак, спрос — это потребность покупателей в некотором товаре, обеспеченная их платежеспособностью (то есть у них есть деньги, чтобы удовлетворить свою потребность). А величина спроса — конкретное количество товаров, которое покупатели хотят и могут (у них есть на это деньги) купить.

Пример: Даша хочет яблок и у нее есть деньги на их покупку — это спрос. Даша идет в магазин и покупает 3 яблока, потому что она хочет купить именно 3 яблока и у нее достаточно денег на эту покупку — это величина (объем) спроса.

Различают следующие виды спроса:

индивидуальный спрос — отдельного конкретного покупателя;
общий (совокупный) спрос — всех покупателей имеющихся на рынке.

Спрос, зависимость между его величиной и ценой (а также другими факторами) можно выразить математически, в виде функции спроса и кривой спроса (графическая интерпретация).

Функция спроса — закон зависимости величины спроса от различных факторов оказывающих на него влияние.

Кривая спроса — графическое выражение зависимости величины спроса на некоторый товар от цены на него.

В простейшем случае функция спроса представляет собой зависимость его величины от одного ценового фактора:

где: Q_D — величина спроса на данный товар;

P — цена на данный товар.

Графическое выражение этой функции (кривая спроса) — прямая линия с отрицательным углом наклона. Описывает такую кривую спроса обычное линейное уравнение:

где: Q_D — величина спроса на данный товар;

P — цена на данный товар;

a — коэффициент задающий смещение начала линии по оси абсцисс (X);

b — коэффициент задающий угол наклона линии (отрицательное число).

Но, в реальности, конечно все намного сложнее и на величину спроса влияет не только цена, но и многие неценовые факторы. В этом случае функция спроса приобретает следующий вид:

где: Q_D — величина спроса на данный товар;

P_X — цена на данный товар;

P₁..P_n — цена на другие взаимосвязанные товары (заменители, дополнители);

I — доход покупателей;

E — ожидания покупателей относительно роста цен в будущем;

N — количество возможных покупателей в данном регионе;

T — вкусы и предпочтения покупателей (привычки, следование моде, традициям и пр.);

Графически такую кривую спроса можно представить в виде дуги, но это опять же упрощение — в реальности график спроса может иметь любую самую причудливую форму.

Таким образом, факторы влияющие на спрос:

Ценовой фактор спроса — цена на данный товар;
Неценовые факторы спроса:
- наличие взаимосвязанных товаров (заменителей, дополнителей);
- уровень доходов покупателей (их платежеспособность);
- количество покупателей в данном регионе;
- вкусы и предпочтения покупателей;
- ожидания покупателей (относительно роста цен, будущих потребностей и пр.);
- иные факторы.

Закон спроса

Для понимания рыночных механизмов очень важно знать базовые законы рынка, к числу которых относится закон спроса и предложения.

Закон спроса — при росте цены на товар, спрос на него снижается, при прочих неизменных факторах, и наоборот.

Математически закон спроса означает наличие между величиной спроса и ценой обратной зависимости.

С обывательской точки зрения закон спроса полностью логичен — чем ниже цена на товар, тем привлекательнее его покупка и тем большее количество единиц товара будет куплено.

Но, как это ни странно, бывают парадоксальные ситуации, при которых закон спроса дает сбой и действует в обратную сторону. Это проявляется в том, что величина спроса растет по мере роста цены! Примерами могут служить эффект Веблена или товары Гиффена.

Закон спроса имеет теоретическое обоснование. В его основе лежат следующие механизмы:

1. Эффект дохода — стремление покупателя приобрести большее количество данного товара при снижении цены на него, при этом не уменьшая объема потребления других товаров.

2. Эффект замещения — готовность покупателя при снижении цены на данный товар отдать предпочтение именно ему, отказавшись от других более дорогостоящих товаров.

3. Закон убывающей предельной полезности — по мере потребления данного товара каждая его дополнительная единица будет приносить все меньшее удовлетворение (продукт «приедается»). Поэтому потребитель будет готов продолжать покупать данный товар только при снижении его цены.

Таким образом, изменение цены (ценового фактора) приводит к изменению величины спроса. Графически это выражается в перемещении по кривой спроса.

Воздействие иных (неценовых) факторов приводит к сдвигу кривой спроса — изменению спроса. При росте спроса график смещается вправо и вверх, при снижении спроса — влево и вниз. Рост называется — расширение спроса, снижение — сужение спроса.

Эластичность спроса

При росте цены на товар, величина спроса на него уменьшается. При снижении цены — увеличивается. Но это происходит по-разному: в одних случаях незначительное колебание уровня цен может вызвать резкий рост (падение) спроса, в других изменение цены в очень широких пределах практически никак не повлияет на спрос. Степень такой зависимости, чувствительности величины спроса к изменению цены или других факторов называется эластичностью спроса.

Эластичность спроса — степень изменения величины спроса при изменении цены (или другого фактора) в ответ на изменение цены или другого фактора.

Числовой показатель, отражающий степень подобного изменения — коэффициент эластичности спроса.

Соответственно, эластичность спроса по цене показывает насколько изменится объем спроса при изменении цены на 1%.

Дуговая эластичность спроса по цене — применяется, когда нужно вычислить примерную эластичность спроса между двумя точками на дуговой кривой спроса. Чем более выпуклой будет дуга спроса, тем выше будет погрешность определения эластичности.

где: E_P D — эластичность спроса по цене;

P₁ — первоначальная цена на товар;

Q₁ — первоначальная величина спроса на товар;

P₂ — новая цена;

Q₂ — новая величина спроса;

ΔP — приращение цены;

ΔQ — приращение величины спроса;

P_ср. — средняя цены;

Q_ср. — средняя величина спроса.

Точечная эластичность спроса по цене — применяется тогда, когда задана функция спроса и есть значения исходной величины спроса и уровня цены. Характеризует относительное изменение величины спроса при бесконечно малом изменении цены.

где: dQ — дифференциал величины спроса;

dP — дифференциал цены;

P₁, Q₁ — значение цены и величины спроса в анализируемой точке.

Эластичность спроса можно рассчитать не только по цене, но например, по доходу покупателей, а также по другим факторам. Существует и перекрестная эластичность спроса. Но мы не будем здесь настолько глубоко рассматривать эту тему, ей будет посвящена отдельная статья.

В зависимости от абсолютного значения коэффициента эластичности различают следующие виды спроса (виды эластичности спроса):

Совершенно неэластичный спрос или абсолютная неэластичность (|E| = 0). При изменении цены величина спроса практически не меняется. Близкими примерами могут служить товары первой необходимости (хлеб, соль, лекарства). Но в реальности нет товаров с совершенно неэластичным спросом на них;
Неэластичный спрос (0 ГРАФИК

Предложение: понятие, функция, график

Теперь поговорим о другом рыночном явлении, без которого невозможен спрос, его неразлучном спутнике и противоборствующей силе — предложении. Здесь также следует различать само предложение и его величину (объем).

Предложение (англ. «Supply») — способность и готовность продавцов продать товар по данной цене.

Величина предложения (объем предложения) — количество товаров, которое продавцы желают и могут продать по данной цене.

Различают следующие виды предложения:

индивидуальное предложение — конкретного отдельного продавца;
общее (совокупное) предложение — всех продавцов присутствующих на рынке.

Функция предложения — закон зависимости величины предложения от различных факторов оказывающих на него влияние.

Кривая предложения — графическое выражение зависимости величины предложения на некоторый товар от цены на него.

Упрощенно функция предложения представляет собой зависимость его величины от цены (ценового фактора):

где: Q_S — величина предложения на данный товар;

P — цена на данный товар.

Кривая предложения в этом случае — прямая линия с положительным углом наклона. Описывает эту кривую предложения следующее линейное уравнение:

где: Q_S — величина предложения на данный товар;

P — цена на данный товар;

c — коэффициент задающий смещение начала линии по оси абсцисс (X);

d — коэффициент задающий угол наклона линии.

Функция предложения, в ее более сложной форме учитывающей влияние и неценовых факторов, представлена ниже:

где: Q_S — величина предложения;

P_X — цена данного товара;

P₁..P_n — цены других взаимосвязанных товаров (заменителей, дополнителей);

R — наличие и характер производственных ресурсов;

K — применяемые технологии;

C — налоги и дотации;

X — природно-климатические условия;

В этом случае кривая предложения будет иметь форму дуги (хотя это опять же упрощение).

Таким образом, факторы влияющие на предложение:

Ценовой фактор — цена на данный товар;
Неценовые факторы:
- наличие товаров-дополнителей и товаров-заменителей;
- уровень развития технологий;
- количество и доступность необходимых ресурсов;
- природные условия;
- ожидания продавцов (производителей): социальные, политические, инфляционные;
- налоги и дотации;
- тип рынка и его емкость;
- прочие факторы.

Закон предложения

Закон предложения — при росте цены на товар, предложение на него увеличивается, при прочих неизменных факторах, и наоборот.

Математически закон предложения означает, что между величиной предложения и ценой существует прямая зависимость.

Закон предложения, также как и закон спроса, очень логичен. Естественно, что любой продавец (производитель) стремится подать свой товар по более высокой цене. Если уровень цен на рынке повышается — продавцам выгодно продавать больше, если снижается — нет.

Изменение цены на товар приводит к изменению величины предложения. На графике это проявляется движением по кривой предложения.

Изменение неценовых факторов приводит к сдвигу кривой предложения (изменению самого предложения). Расширение предложения — сдвиг кривой предложения вправо и вниз. Сужение предложения — сдвиг влево и вверх.

Эластичность предложения

Предложении, как и спрос, может находиться в различной степени зависимости от изменения цены и других факторов. В этом случае говорят об эластичности предложения.

Эластичность предложения — степень изменения величины предложения (количества предлагаемых товаров) в ответ на изменение цены или другого фактора.

Числовой показатель, отражающий степень такого изменения — коэффициент эластичности предложения.

Соответственно, эластичность предложения по цене показывает насколько изменится величина предложения при изменении цены на 1%.

Формулы для расчета дуговой и точечной эластичности предложения по цене (Eps) полностью аналогичны формулам для спроса.

Виды эластичности предложения по цене:

абсолютно неэластичное предложение (|E| = 0). Изменение цены совершенно не влияет на величину предложения. Это возможно в краткосрочном периоде;
неэластичное предложение (0 Рыночное равновесие графически выражается пересечением графиков спроса (D) и предложения (S) в одной точке. Этой точке рыночного равновесия соответствуют: P_E — равновесная цена, и Q_E — равновесный объем.

Есть разные теории и подходы объясняющие как именно устанавливается рыночное равновесие. Самые известные — подход Л. Вальраса и А. Маршалла. Но это, также как паутинообразная модель равновесия рынка продавца и рынка покупателя — тема для отдельной статьи.

Если очень кратко и упрощенно, то механизм рыночного равновесия можно объяснить следующим образом. В точке равновесия все (и покупатели, и продавцы) довольны. Если одна из сторон получает преимущество (отклонение рынка от точки равновесия в ту или другую сторону), другая сторона будет недовольна и первой из сторон придется пойти на уступки.

Например: цена выше равновесной. Продавцам выгодно продавать товар по более высокой цене и предложение повышается, возникает избыток товаров. А покупатели будут недовольны ростом цены на товар. Вдобавок конкуренция высокая, предложение избыточно и продавцам, чтобы реализовать товар придется снизить цену, пока она не придет к равновесному значению. При этом снизится и объем предложения до равновесного объема.

Или другой пример: объем предлагаемых на рынке товаров меньше равновесного объема. То есть на рынке дефицит товаров. В таких условиях покупатели готовы заплатить большую цену за товар, чем та по которой он продается в данный момент. Это побудит продавцов увеличивать объемы предложения с одновременным повышением цены. В итоге цена и объем спроса/предложения придут к равновесному значению.

По сути это была иллюстрация к теориям рыночного равновесия Вальраса и Маршалла, но как уже говорилось, более подробно рассмотрим их в другой статье.

Галяутдинов Р. Р. Обзорные лекции для подготовки к госэкзаменам по специальности «Экономика и управление на предприятии». 2012.

Задача №169. Нахождение уравнений кривых спроса и предложения

Спрос и предложение на рынке на товар задаются линейными уравнениями. Известно, что равновесная цена равна 200 руб. за упаковку товара, а равновесное количество — 100 упаковок в день. В точке равновесия однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5% и повышение величины предложения на 0,5%.

Определите уравнения кривых спроса и предложения, считая их линейными.

Решение:

Общая точка двух прямых спроса и предложения имеет координаты:

Общий вид линейной функции спроса:

Так как однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5%, следовательно, коэффициент эластичности спроса равен:

Запишем формулу точечной эластичности спроса по цене:

Подставим имеющиеся по условию данные:

Тогда функция спроса на данный товар имеет вид:

Общий вид линейной функции предложения:

Так как однопроцентное повышение цены на данный товар влечет повышение величины предложения на 0,5%., следовательно, коэффициент эластичности предложения равен:

Формула эластичности предложения будет иметь вид:

Подставим имеющиеся по условию данные:

Тогда функция предложения на данный товар имеет вид:

Функция спроса (прямая и обратная) с примерами и графиками движения и сдвига

Функция спроса — это математическое уравнение, которое выражает спрос на продукт или услугу в зависимости от его цены и других факторов, таких как цены на заменители и дополнительные товары, доход и так далее.

Функция спроса создает связь между спросом (требуемым количеством) на продукт (который является зависимой переменной) и факторами, влияющими на спрос, такими как цена продукта, цена замещающих и дополняющих товаров, средний доход и прочие (которые являются независимыми переменными).

Давайте рассмотрим рынок приложений для найма автомобиля с водителем и выясним факторы, которые могут повлиять на ежедневный пробег таксистов, предлагающих данный вид услуги.

Множественный регрессионный анализ

Самым важным фактором является стоимость проезда (цена, взимаемая за километр пути).

Другие потенциальные факторы являются детерминантами спроса, включая цену заменителей, то есть цену общественного транспорта или конкурирующих услуг такси независимо от того, рабочий или выходной день, ясная или дождливая погода и так далее.

Один из методов создания функции спроса заключается в использовании множественного регрессионного анализа для выяснения взаимосвязи между требуемым количеством, ценой продукта и всеми другими факторами.

Множественный регрессионный анализ присваивает различные коэффициенты каждому из факторов, влияющих на спрос. Знак коэффициента — положительный или отрицательный — говорит нам, связаны ли спрос и фактор положительно или отрицательно.

Предположим для упрощения, что вы использовали только две переменные — (1) цену самого продукта и (2) рост цены конкурирующего общественного транспорта — и пришли к следующему уравнению:

Q = 1,200,000 – 150,000 × P + 200,000 × P_PT, где

Q — это потребляемые километры,

P — цена за километр услуги по вызову пассажиров,

P_PT — увеличение цены за поездку в системе общественного транспорта.

Параметр Р имеет отрицательный знак, который показывает, что с каждым долларовым увеличением стоимости проезда за километр требуемое количество будет уменьшаться на 150 000 километров в день.

С другой стороны, параметр P_PT имеет положительный знак, а это означает, что увеличение платы за проезд в общественном транспорте на один доллар приведет к увеличению спроса на 200 000 километров.

Поскольку приведенное выше уравнение создает связь не только между требуемыми километрами и взимаемой ценой, но и с ценой заменителя, оно представляет собой как сдвиг кривой спроса, так и движение вдоль кривой спроса.

До тех пор, пока цены на общественный транспорт не изменятся, мы можем упростить функцию спроса до соотношения между Q и P:

Q = 1,200,000 – 150,000 × P

Мы можем разработать график спроса, используя приведенное выше уравнение, просто подключив различные цены за километр.

Обратная функция спроса

График спроса и предложения обычно строится таким образом, что количество находится на оси X, а цена — на оси Y, но функция спроса, которую мы определили выше, имеет цену (P) как независимую переменную и количество (Q) как независимую переменную.

Функция спроса иногда определяется ценой P как независимой переменной. Такая функция спроса называется обратной функцией спроса.

С помощью всего лишь нескольких математических манипуляций мы можем преобразовать функцию спроса, определенную выше, в обратную функцию спроса:

150,000 × P = 1,200,000 – Q

P = (1,200,000 – Q) / 150,000

P = 8 – Q / 150,000

Обратная функция спроса полезна, когда мы заинтересованы в поиске предельного дохода, дополнительного дохода, полученного от одной проданной дополнительной единицы.

Функция предельного дохода является первой производной от обратной функции спроса. Для обратной функции спроса вида P = a — bQ функция предельного дохода равна MR = a — 2bQ. Функция предельного дохода в данном случае выглядит следующим образом:

P = 8 – 2 × Q / 150,000 = 8 – Q / 75,000

Примеры и графики

Давайте выясним, каков объем перевозок в километрах будет востребован при следующих сценариях: (A) средняя цена за километр (Р) составляет $ 1.5 и $ 1.75; и (B) средняя цена за километр (Р) составляет $ 1.5, а рост цен на общественный транспорт (Р_РТ) — $ 0.25

Сценарий А

Следующее уравнение показывает требуемое количество, соответствующее каждой цене:

Q_1.50 = 1,200,000 – 150,000 × $ 1.50 = 975,000

Q_1.75 = 1,200,000 – 150,000 × $ 1.75 = 937,500

Сценарий В

В этом случае происходит изменение цены заменителя, поэтому она представляет собой сдвиг кривой:

Q_1.50;0.25 = 1,200,000 – 150,000 × $ 1.50 + 200,000 × $ 0.25 = 1,025,000

В нашем примере Q_1.50;0.25 выше, чем Q_1.50, потому что рост цен на общественный транспорт вызвал внешний сдвиг кривой спроса.

На следующей диаграмме показано движение вдоль начальной кривой спроса в сценарии А и сдвиг в случае сценария B:

источники:

http://ecson.ru/economics/demand-and-supply/zadacha-169.nahozhdenie-uravneny-krivyh-sprosa-i-predlozheniya.html

http://sprintinvest.ru/funkciya-sprosa-pryamaya-i-obratnaya-s-primerami-i-grafikami-dvizheniya-i-sdviga

Источник

Потребительский
излишек, как площадь под кривой спроса,
лежащую выше линии цены, можно определить
с помощью интегрального исчисления.
Особенно этот метод полезен в случае
нелинейной функции спроса.

Продемонстрируем
возможности метода на простом примере.
На рис. 5-1 изображена функция спроса
P
= f(Q),
уравнение которой:

Обозначим
цену, по которой потребитель покупает
товар Х (руб. за единицу) какР^*,
а количество товара, которое он покупает
(единиц в неделю) как Q^*.
Тогда потребительский излишек, как
площадь заштрихованного треугольника,
на рис. 5-1 будет:

Поскольку
в нашем примереР^*=15,
а Q^*=6,
то:

Так
как здесь мы имели дело с линейной
функцией, то этот результат, конечно,
легче было получить геометрическим
способом (см. пояснения к рис. 5-1). В случае
же нелинейной функции спроса рассчитать
CS
без методов интегрального исчисления
невозможно.

—————————————————————————————————

Подход
Хикса. Компенсирующая и эквивалентная
вариации дохода

Все
же положение о том, что сумма, которую
действительно платят за товар потребители,
ниже удовлетворения, которое они от
этого товара получают, оказалось слишком
важным, чтобы отбросить его из-за проблемы
измерения. Дж. Хикс, продолжил исследование
и предложил несколько способов измерения
потребительского излишка, позволяющих
избавиться от искажающего эффекта
дохода.

Первый
способ измерения получил название
компенсирующей
вариации дохода
(CV
– compensating
variation).
Компенсирующая вариация дохода показывает
сколько денег следует дать потребителю
после
изменения цены, чтобы его благосостояние
осталось точно таким же, каким оно было
до изменения цены. Предположим, цена
товара повысилась. Естественно, что
это, при прочих равных условиях, ухудшает
положение потребителя. Насколько?
Размеры потери в благосостоянии можно
определить, если спросить у потребителя,
при какой минимальной сумме компенсации
он согласился бы покупать по новым
ценам. Ответ (разумеется, честный) на
этот вопрос и даст величину компенсирующей
вариации дохода.

На
языке геометрии CV
– это ответ на вопрос, как сильно мы
должны сдвинуть новую бюджетную линию
АС (наклон
линии равен новой, более высокой цене)
вверх, чтобы она стала касательной к
кривой безразличия U₁
(см. рис. 5-3). Исходное равновесие
потребителя в точке Е₁лежит на
бюджетной линии АВ.
Повышение цены товара Х
поворачивает бюджетную линию в положение
АС.
Благосостояние потребителя падает –
он переходит на более низкую кривую
безразличия U₀.
Чтобы восстановить благосостояние
потребителя при новой цене (вернуть его
на кривую безразличия U₁)
нужно увеличить его денежный доход на
величину CV (сдвинуть
линию АС
вверх в
положение пунктирной линии так, чтобы
она коснулась U₁).
Тогда потребитель, получивший компенсацию
CV
будет иметь доход достаточный для того,
чтобы купить новый оптимальный набор
Е′,
равноценный
набору Е₁.
Какова же потеря потребительского
излишка от повышения цены? Она точно
равна величине компенсирующей добавки
CV.

Второй
способ измерения потребительского
излишка – эквивалентная
вариация дохода,
EV
(equivalent variation). В этом случае об изменении
потребительского излишка, судят по
тому, сколько денег следовало бы забрать
у потребителя до
изменения
цены, чтобы
его благосостояние было точно таким
же, каким оно стало после изменения
цены. Эта мера называется эквивалентной
вариацией дохода, потому что она
представляет собой изменение дохода,
которое с точки зрения полезности,
эквивалентно последствиям изменения
цены. Чтобы определить EV
нужно
спросить у потребителя, какую максимальную
сумму он согласился бы отдать за то,
чтобы избежать изменения цены, то есть
отдать за возможность покупать товар
по старым ценам.

Геометрически
найти EV
значит определить, насколько мы должны
сдвинуть исходную бюджетную линию вниз
(при повышении цены), чтобы она коснулась
той кривой безразличия, на которой
окажется потребитель после изменения
цены.

На
рис. 5-4 первоначально потребитель
находится в равновесии в точкеЕ₁.
Повышение цены товара Х,
меняет бюджетное ограничение для
потребителя с АВ
на АС и
побуждает
его выбрать новый оптимальный набор
Е₂,
находящийся на более низкой кривой
безразличия U₀.
Потеря в благосостоянии для потребителя
эквивалентна той денежной сумме, которую
он максимально готов отдать за возможность
покупать товар по старой цене. Если бы
его доход уменьшился на величину AF
при сохранении
старой цены (графически – это сдвиг
бюджетной линии АВ
вниз в положение пунктирной линии), то
он выбрал бы набор Е′,
полезность которого для него точно
равнялась бы полезности набора Е₂.
Таким образом потребителю было бы всё
равно – покупать ли по новой, более
высокой цене и прежнем доходе ОА
набор Е₂,
или покупать по старой, более низкой
цене и уменьшенном доходе ОF
набор Е′.
Следовательно за возможность покупать
товар по старой цене потребитель готов
отдать сумму не превышающую
AF. Эта сумма
и представляет собой эквивалентное
изменение (вариацию) дохода,
EV.

Обе
версии измерения потребительского
излишка теоретически правомерны и
могут использоваться в решении проблем
социально-экономической политики. Если
речь идёт о том, чтобы компенсировать
потерю благосостояния потребителям в
связи с возросшими ценами на какие-либо
товары, целесообразно использовать
концепцию компенсирующей вариации
дохода. Если решается вопрос о том, на
какие товары повышать косвенный налог,
и правительство желает сделать это с
меньшими потерями для благосостояния
потребителей, тогда более уместна
концепция эквивалентной вариации
дохода.

Впрочем,
существует одно серьёзное препятствие
– информация, необходимая для расчёта
EV и
CV, практически
недоступна. Кривые безразличия являются
полезными аналитическими инструментами,
помогающими нам понять человеческое
поведение, но было бы серьёзной ошибкой
думать о них как о вещах, которые можно
обнаружить и измерить. В действительности
у нас нет точных данных не только о
предпочтениях других людей, но даже и
о собственных предпочтениях. В этом
смысле подход А. Маршалла к определению
потребительского излишка на основе
обычной кривой спроса практически более
приемлем. Но насколько он правомерен?

Современный
потребитель, как правило, распределяет
свой доход среди большого количества
разных товаров, да и изменения относительных
товарных цен обычно незначительны.
Поэтому эффект дохода, возникающий при
изменении цен отдельных товаров часто
столь мал, что им можно пренебречь.
Поэтому величина потребительского
излишка по Маршаллу (как площадь под
обычной кривой спроса) почти не отличается
от потребительского излишка рассчитанного
по Хиксу (EV
,СV
и как площадь под кривой спроса с
компенсированным доходом). Вот почему
современные экономисты в подавляющем
большинстве случаев отдают предпочтение
подходу Маршалла.

От
индивидуального спроса к рыночному
спросу

Мы
вывели кривую индивидуального
спроса и объяснили с помощью эффектов
дохода и замещения её отрицательный
наклон. Но в большинстве исследований
используется кривая рыночного
спроса.

Мы
видели также как поведение отдельного
потребителя определяет кривую спроса,
то есть связь между ценой, по которой
он мог бы купить товар, и количеством,
которое он решает купить. На большинстве
рынков все потребители покупают товар
по одной цене, поэтому можно говорить
о единой рыночной цене и единой кривой
спроса, представляющей общий спрос всех
потребителей на данный товар как функцию
его цены. Так как общее количество, на
которое предъявляется спрос при любом
уровне цены это количество которое
хочет купить первый потребитель по
данной цене плюс количество, которое
хочет купить второй потребитель по
данной цене плюс … то кривая
рыночного спроса представляет
собой горизонтальную сумму всех
индивидуальных кривых спроса,
как показано на рис. 5-6.

Предположим
на рынке действуют три покупателя, спрос
каждого из которых представлен на
графике линейной кривой спроса d₁,
d₂
и d₃.

Покажем
сначала, как можно сложить кривые
индивидуального спроса геометрически.
Затем рассмотрим алгебраическое решение
задачи.

Поскольку
все функции индивидуального спроса
линейны, постольку сложение их даёт
тоже линейную функцию рыночного спроса.
Но полученная линия будет ломаной,
состоящей из нескольких отрезков, каждый
из которых соответствует определённому
диапазону изменения цены. Найдём
критические точки, соединив которые мы
получим эту ломаную кривую.

При
рыночной цене Р₃
величина спроса на рынке равна 0, так
как ни один из потребителей не готов
покупать по этой цене даже единицу
товара Х (D
= d₁+d₂+d₃= 0+0+0 =
0). Мы получили
первую точку на кривой рыночного спроса,
а
с координатами (0,Р₃).

В
диапазоне цены между Р₃
и Р₂
единственным
покупателем товара является 3-й
потребитель. Рыночный спрос при цене
Р₂
равен: D
= d₁+d₂+d₃= 0+0+2 =
3.
Координаты
второй точки кривой рыночного спроса,
b –
(2,P₂).
Поэтому в этом ценовом диапазоне рыночная
кривая спроса совпадает с d₃
на участке
ab.

В
ценовом диапазоне Р₂
– Р₁
спрос предъявят 1-й и 3-й потребители.
При цене Р₁
величина рыночного спроса составит
D
= d₁+d₂+d₃= 3+0+8 =
11. Координаты
с
— следующей точки кривой рыночного
спроса – (11,Р₁).
Соединив прямой линией точки b
и c,
получим участок кривой рыночного спроса
bc.

Наконец,
при Р=0 все три потребителя предъявят
спрос: D
= d₁+d₂+d₃=
5+8+12=25. Соединив
прямой линией точку f
(25,0)
с точкой с,
получим последний участок кривой
рыночного спроса сf.

Как
получить уравнение функции рыночного
спроса, если известны уравнения функций
индивидуального спроса?

Изображённые
на рис. 5-6 функции индивидуального
спроса, описываются уравнениями:

Спрос
1-го потребителя: Q₁
= 5 – 0,5P;
(1)

Спрос
2-го потребителя: Q₂
= 8 – 2P;
(2)

Спрос
3-го потребителя: Q₃=
12 – P

(3)

Для
того, чтобы определить какой будет
величина совокупного спроса при любом
уровне цены на рынке, нужно алгебраически
сложить уравнения индивидуального
спроса: Q^d_рын.
= Q₁+
Q₂
+Q₃.

Однако
простое решение: Q^d_рын
= 25 – 3,5Р,
было бы ошибочным, поскольку оно не
учитывает того, что в некоторых ценовых
диапазонах рыночный спрос состоит из
спроса не всех, а только отдельных
потребителей. Поэтому при суммировании
приходится эти диапазоны учитывать.
Определим их.

Из
уравнения (3) найдем, что при Р ≥
12 спрос 3-го потребителя будет равен
нулю (на рис. 5-6 Р₃=12).
Из уравнения (2) следует, что если Р≥
10,
то спрос 2-го потребителя равен 0 ( на
рис. 5-6 этому уровню цены соответствует
Р₂.
Из уравнения
(1)
находим, что при Р≥
4 спрос 1-го потребителя тоже равен 0.

Следовательно,
если 10 ≤

Р
≤ 12,
то рыночный спрос состоит только из
спроса 3-го потребителя. В этом ценовом
диапазоне уравнение функции рыночного
спроса
представлено только уравнением (3): Q^d_рын
=Q₃=
12 – P.

В
диапазоне 4 ≤ Р ≤ 10
спрос
на рынке предъявляют
3-й
и 1-й потребители. Поэтому на этом участке
рыночный спрос: Q^d_рын.
= Q₁+
Q₃
=
(5
– 0,5Р) + (12 – Р) = 17 – 1,5Р.

Наконец,
если
0 ≤ Р ≤ 4, то
Q^d_рын.
= Q₁+
Q₂
+Q₃
= (5 – 0,5Р) + (8 – 2Р) + (12 – Р) = 25 –3,5Р.

Понятно,
что кривая рыночного спроса, являясь
горизонтальной суммой нисходящих
индивидуальных кривых спроса, также
имеет отрицательный наклон. Даже, если
некоторые потребители имеют восходящую
кривую спроса, то они не делают погоды
на данном рынке, так как подавляющее
большинство покупателей имеют нормальные,
нисходящие кривые спроса. Это ещё одна
причина, по которой мы можем не беспокоиться
о товаре Гиффена в дальнейшем анализе.

Есть
несколько интересных случаев, когда
рыночный спрос формируется не как
простая сумма спроса отдельных
покупателей. Эти случаи – так называемый
«эффект повального увлечения» (bandwagon
effect),
«эффект сноба» и «эффект Веблена».

Эффект
повального увлечения
состоит в том, что когда цена товара
падает и спрос на него возрастает,
отдельные покупатели, желая «быть не
хуже других», или не «отстать от моды»,
также
увеличивают свой спрос. Примерами могут
служить спрос на гротескно тупоносую
обувь, спрос на мобильные телефоны,
спрос молодых людей на пиво, которое
можно распивать идя по улице, и т.п. В
результате спрос расширяется в большей,
чем прогнозировалось степени за счёт
дополнительных покупателей. Это означает,
что рыночная кривая спроса не может
быть просто суммой индивидуальных
кривых спроса. Она будет иметь более
пологий уклон, чем тот который имел бы
место без описанного эффекта. На рис.
5-7 линия D₁
– это кривая рыночного спроса как
горизонтальная сумма спроса всех
потребителей, каждый из которых считает,
что на рынке будет продано Q₁
единиц (точка а).
Если цена упадёт до Р₂,
то эффекты дохода и замещения, как
предсказывает линия D₁,
приведут к росту величины спроса до Q₂
(точка b).
Q₂больше,
чем Q₁.
Люди увидят, что рыночные продажи больше,
чем они ожидали. Они «присоединятся к
толпе». Линия Dначнёт
сдвигаться вправо. Если цена будет
оставаться на уровне Р₂,
этот
сдвиг прекратится, когда линия спроса
достигнет положения D₂.
Точка с
показывает, какими действительно будут
продажи (Q₃
по
цене
Р₂₎.
Соединив точки а и с, получим кривую
рыночного спроса, учитывающую эффект
повального увлечения. Эта кривая будет
более пологой, чем обычная кривая спроса.

Э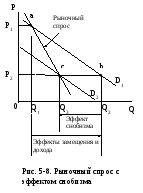ффект
сноба
заключается в том, что при снижении цены
на товар, когда некоторые группы общества
расширяют потребление этого товара,
другие группы снижают его, чтобы
«выделиться из толпы». Этот эффект
противоположен эффекту повального
увлечения. Рыночная кривая спроса в
этом случае может демонстрировать
больший наклон, чем тот который может
быть предсказан при прямолинейном
агрегировании индивидуальных кривых
спроса.

На
рис. 5-8 прогнозируемый потребителями
спрос (в соответствие с агрегированной
кривой рыночного спроса D₁)
составляет Q₁.
При снижении цены до Р₂
спрос Q₂
оказывается
большим, чем ожидаемый Q₁.
Некоторые потребители, чтобы «не быть
как все» сокращают свой спрос ( кривая
D₁
сдвигается влево). Если цена на рынке
остаётся на уровне Р₂,
то кривая спроса будет сдвигаться до
положения D₂,
и объём спроса составит Q₃.
Соединив прямой линией две точки – а
и с,
получим рыночную кривую спроса, более
крутую, чем кривые, не учитывающие эффект
снобизма.

Если
бы эффект снобизма по своей величине
превосходил эффекты дохода и замещения,
то величина рыночного спроса с понижением
цены стала бы меньше Q₁
(на графике точка с
находилась бы левее и ниже точки а
как
на рис. 5-9). Тогда кривая рыночного спроса
приобрела бы положительный наклон. Но
это невозможно, так как низкий рыночный
спрос побудил бы снобов покупать больше.

Э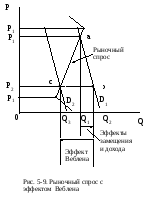ффект
Веблена
(эффект престижного потребления)
названный по имени открывшего его
американского экономиста и социолога
Торстейна Веблена (1857-1929) возникает
тогда, когда в результате падения цены
товара некоторые потребители решают,
что это произошло из-за ухудшения его
качества или утери им «исключительности»
в глазах общества, и сокращают потребление
этого товара. И наоборот, рост цены
товара ведёт к увеличению покупок.
Вследствие этого рыночная кривая спроса
приобретает более крутой наклон, чем
прогнозируемый (как на рис. 5-8). Она может
даже стать восходящей(то есть иметь
положительный наклон), что противоречит
закону спроса.

Предположим,
что цена товара падает с Р₁
до Р₂
(рис. 5-9). В отсутствие эффекта Веблена,
это привело бы к движению вниз вдоль
агрегированной кривой спроса D₁
из точки а
в точку b.
Под действием эффекта дохода и замещения
величина спроса увеличилась бы с Q₁
до Q₂.
Однако потребители, ожидавшие, что цена
товара будет Р₁,
снижение цены могут воспринять как
свидетельство того, что данный товар
перестал быть престижным, и они захотят
сократить его потребление (сдвиг кривой
D
в
положение D₂).
Величина спроса поэтому при цене Р₂
понизится до Q₃.
В результате кривая рыночного спроса,
проведённая через точки a
и с,
будет иметь необычный положительный
наклон.

Но
эффект Веблена возможен только в
ограниченном ценовом диапазоне. При
достаточно высокой цене (выше p₁)
потребители столкнутся с бюджетными
ограничениями и не смогут позволить
себе «демонстративное потребление.
Тогда кривая рыночного спроса приобретёт
нормальный отрицательный наклон.

При
достаточно низкой цене (ниже р₁)
каждый может себе позволить покупать
данный товар и этот товар станет
малоподходящим объектом для престижного
потребления. Эффект Веблена в отношении
такого товара вообще не возникнет.
Поэтому кривая рыночного спроса с
эффектом Веблена напоминает букву Z.

Обратная
функция спроса

В
микроэкономическом анализе часто
используется обратная
функция спроса.
В этом случае цена представляется как
функция величины спроса: Р
= g(Q).
Преобразовать обычную, прямую функцию
спроса в обратную очень просто. Предположим
дана функция : Q
= 13 – 2Р.
Обратная функция спроса тогда будет:
Р
= 6,5 – 0,5Q.
На графике обратная функции спроса
выглядит точно так же как прямая функция
(рис. 5-10). Обратная функция спроса
показывает какой должна быть рыночная
цена товара Р,
для того чтобы спрос на него составил
Q
единиц.
В то же время было бы ошибкой считать,
что это функция говорит о том, что
величина спроса определяет рыночную
цену. Каков же тогда экономический смысл
обратной функции спроса?

М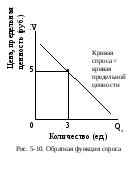ы
уже доказывали, что кривая индивидуального
спроса совпадает с кривой предельной
ценности. Потребитель будет увеличивать
потребление блага до тех пор, пока не
достигнет точки в которой предельная
ценность единицы блага равна его цене.
Так на рис. 5-10, если рыночная цена блага
Х равна 5 рублям, и предельная ценность
для потребителя 1-й, 2-й и 3-й единиц блага
составляют соответственно 6, 5,5 и 5 руб.,
то он приобретёт три единицы. Так как
он будет делать это при любой заданной
цене, то график того, сколько он будет
покупать при любой цене – то же самое,
что график предельной ценности (MV).
Но предельная ценность единицы блага
зависит от количества потребляемого
блага. Следовательно, обратная
функция спроса – это, по сути, функция
предельной ценности. Она
отражает то обстоятельство, что с
увеличением количества потребляемого
блага предельная полезность, а
следовательно и предельная ценность
блага для потребителя падает. Ранее мы
установили также, что высота кривой
спроса в любой её точке равна предельной
норме замещения. Следовательно, обратная
функция спроса показывает предельную
норму замещения, или предельную готовность
потребителя платить за товар, или
предельную ценность товара для
потребителя. Всё это суть одно и то же.

Суммирование
обратных функций индивидуального спроса
отличается от суммирования прямых
функций спроса и по смыслу и технически.
Агрегированная обратная функция спроса
показывает какова общая для всех
потребителей (суммарная) ценность каждой
единицы блага. Здесь уже складываются
не количества блага, а предельные
ценности. Поэтому сложение обратных
функций индивидуального спроса нужно
производить по вертикали, а не по
горизонтали. Эта операция будет иметь
экономический смысл в том случае, если
благо потребляется индивидами совместно.
Такие экономические блага существуют
и называются общественными благами.
Обратная функция спроса нам очень
пригодится в теории общественных благ,
которую мы рассмотрим в конце курса.

Эластичность
спроса по цене: углубление анализа

Анализируя
поведение потребителя, мы обосновали
закон спроса. Если цена на товар растёт,
то, ceteris
paribus
(при прочих равных условиях), величина
спроса на этот товар на рынке уменьшается,
и наоборот. Но вот на сколько? Это зависит
от чувствительности спроса к изменению
цены, то есть от ценовой
эластичности спроса.
Знание эластичности спроса по цене
имеет большое практическое значение.
В правильной оценке эластичности спроса
заинтересованы и фирмы, и правительство.

Напомним,
что для измерения эластичности
используетсякоэффициент
эластичности спроса (E^D),
который в самом общем виде представляет
собой отношение процентного изменение
величины спроса к процентному изменению
цены:

Коэффициент
эластичности показывает, на сколько
процентов изменится спрос, если цена
изменится на 1 %. Поскольку цена и величина
спроса изменяются (по закону спроса) в
противоположном друг другу направлении,
постольку коэффициент эластичности
имеет знак «минус» , который, впрочем,
экономисты по молчаливому соглашению
часто опускают. К примеру, |
Е^d|
для
электроэнергии равняется 0,13 – это
значит, что если тариф на электроэнергию
повысится на 1 % , то спрос на неё понизится
на 0,13 %. Если тариф повысится на 10 %, то
спрос понизится на 1,3 % и т.д.

Напомним
также, что в зависимости от степени
чувствительности спроса к изменению
цены можно выделить пять видов
эластичности:

Эластичный
спрос.
Покупатели чувствительны к изменению
цены. Спрос в процентном отношении
изменяется больше, чем цена, то есть
для эластичного спроса |
Е^d|
> 1,0;
Неэластичный
спрос.
Покупатели нечувствительны к изменению
цены. Спрос в процентном отношении
изменяется меньше, чем цена, то есть
для эластичного спроса |
Е^d|
< 1,0;
Единичная
эластичность спроса.
Спрос в процентном отношении изменяется
так же как цена, то есть для этого вида
спроса |
Е^d|
=1,0;
Совершенно
эластичный спрос.
Покупатели гиперчувствительны к
изменению цены. Например, при ничтожно
малом повышении цены спрос стремится
к бесконечно малой величине. Для этого
вида спроса|
Е^d|
= ∞. На графике кривая спроса
представляет собой прямую линию
параллельную абсциссе;
Совершенно
неэластичный спрос.
Покупатели абсолютно нечувствительны
к изменению цены. При любом процентном
изменении цены величина спроса остаётся
неизменной. Для этого вида спроса |
Е^d|
=0. На
графике кривая спроса представляет
собой прямую линию параллельную
ординате.

Существуют
два способа точного измерения эластичности.
Ценовую эластичность спроса можно
определить: (1) в некотором диапазоне
изменения цены – на отрезке (дуге) кривой
спроса. Этот способ измерения называется
дуговой
эластичностью;
(2) для определённого уровня цены, то
есть в некоторой точке кривой спроса.
Этот способ называется точечной
эластичностью.

Например,
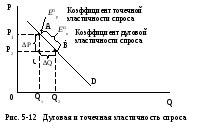
на рис. 5-12 дуговая эластичность измеряется
в ценовом диапазоне Р₁
– Р₂на отрезке
АВ кривой
спроса, а точечная – для уровня цены
Р₁
в точке А.

Выведем
формулу для дуговой эластичности спроса.

Поскольку
в приведенной выше формуле не ясно,
какое значениеQ:
Q₁
или Q₂,
берётся за базу, а это может сильно
повлиять на результат измерения,
экономисты договорились брать среднее
арифметическое значение. То есть, Q
= (Q₁
+ Q₂
/2. То же
самое делается по отношению к цене,
выступающей в качестве базы: Р
= (Р₁
+ Р₂)/2.
Тогда формула
коэффициента дуговой эластичности
спроса по цене примет окончательный
вид:

Д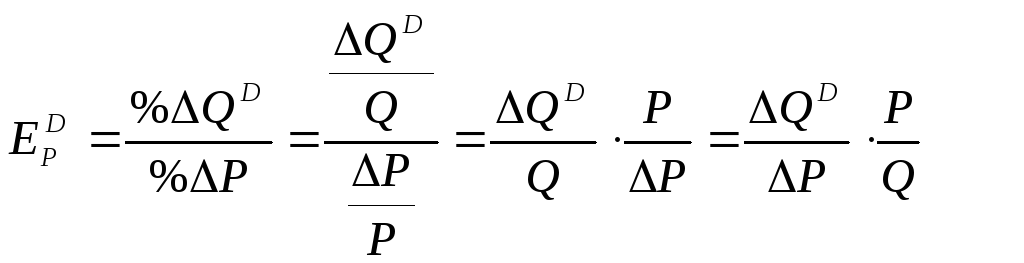уговая
эластичность спроса используется в
случае значительного изменения цены.
Если же это изменение незначительно,
то целесообразно использовать точечную
эластичность спроса. Коэффициент
точечной эластичности спроса легко
выводится из формулы (2):

Посмотрим
на рис. 5-12 и представим, что∆P
сжимается так, что точка С
приближается вплотную к точке А.
Тогда ∆Q
также сжимается и точка В
стремится к точке А
как к своему
пределу. Если мы примем ∆P
и, следовательно,
∆Q
за бесконечно малые величины, то получим
измерение ценовой эластичности в точке
А:

————————————————————————————————

Источник

Содержание

Множественный регрессионный анализ
Обратная функция спроса
Примеры и графики

Функция спроса – это математическое уравнение, которое выражает спрос на продукт или услугу в зависимости от его цены и других факторов, таких как цены на заменители и дополнительные товары, доход и так далее.

Множественный регрессионный анализ

Самым важным фактором является стоимость проезда (цена, взимаемая за километр пути).

Один из методов создания функции спроса заключается в использовании множественного регрессионного анализа для выяснения взаимосвязи между требуемым количеством, ценой продукта и всеми другими факторами.

Множественный регрессионный анализ присваивает различные коэффициенты каждому из факторов, влияющих на спрос. Знак коэффициента – положительный или отрицательный – говорит нам, связаны ли спрос и фактор положительно или отрицательно.

Предположим для упрощения, что вы использовали только две переменные – (1) цену самого продукта и (2) рост цены конкурирующего общественного транспорта – и пришли к следующему уравнению:

Q = 1,200,000 – 150,000 × P + 200,000 × P_PT, где

Q – это потребляемые километры,

P – цена за километр услуги по вызову пассажиров,

P_PT – увеличение цены за поездку в системе общественного транспорта.

С другой стороны, параметр P_PTимеет положительный знак, а это означает, что увеличение платы за проезд в общественном транспорте на один доллар приведет к увеличению спроса на 200 000 километров.

Поскольку приведенное выше уравнение создает связь не только между требуемыми километрами и взимаемой ценой, но и с ценой заменителя, оно представляет собой как сдвиг кривой спроса, так и движение вдоль кривой спроса.

Q = 1,200,000 – 150,000 × P

Обратная функция спроса

График спроса и предложения обычно строится таким образом, что количество находится на оси X, а цена – на оси Y, но функция спроса, которую мы определили выше, имеет цену (P) как независимую переменную и количество (Q) как независимую переменную.

150,000 × P = 1,200,000 – Q

P = (1,200,000 – Q) / 150,000

P = 8 – Q / 150,000

Функция предельного дохода является первой производной от обратной функции спроса. Для обратной функции спроса вида P = a – bQ функция предельного дохода равна MR = a – 2bQ. Функция предельного дохода в данном случае выглядит следующим образом:

P = 8 – 2 × Q / 150,000 = 8 – Q / 75,000

Примеры и графики

Сценарий А

Следующее уравнение показывает требуемое количество, соответствующее каждой цене:

Q_1.50 = 1,200,000 – 150,000 × $ 1.50 = 975,000

Q_1.75 = 1,200,000 – 150,000 × $ 1.75 = 937,500

Сценарий В

В этом случае происходит изменение цены заменителя, поэтому она представляет собой сдвиг кривой:

Q_1.50;0.25 = 1,200,000 – 150,000 × $ 1.50 + 200,000 × $ 0.25 = 1,025,000

Функция спроса и функция предложения могут быть использованы для решения задач рыночного равновесия и рыночной клиринговой цены.

Источник

Задача №36. Определение функции спроса

Известно, что еженедельно на рынке продается 120 ед. товара по цене Р = 12 долл./ед. При условии равновесия на рынке снижение цены на 1% повышает объем спроса на товар на 0,6%. Определите функцию спроса на данный товар, предполагая, что она линейная.

Решение:

Общий вид линейной функции спроса:

При

По определению эластичность спроса по цене показывает, на сколько процентов изменяется величина спроса при изменении цены на 1%.
Так как снижение цены на 1% повышает объем спроса на товар на 0,6%, следовательно,

(Так как зависимость между объёмом спроса и ценой обратная, эластичность спроса по цене — величина отрицательная).

Подставим имеющиеся по условию данные:

Тогда функция спроса на данный товар имеет вид:

Функция спроса (прямая и обратная) с примерами и графиками движения и сдвига

Множественный регрессионный анализ

Самым важным фактором является стоимость проезда (цена, взимаемая за километр пути).

Один из методов создания функции спроса заключается в использовании множественного регрессионного анализа для выяснения взаимосвязи между требуемым количеством, ценой продукта и всеми другими факторами.

Q = 1,200,000 – 150,000 × P + 200,000 × P_PT, где

Q — это потребляемые километры,

P — цена за километр услуги по вызову пассажиров,

P_PT — увеличение цены за поездку в системе общественного транспорта.

Поскольку приведенное выше уравнение создает связь не только между требуемыми километрами и взимаемой ценой, но и с ценой заменителя, оно представляет собой как сдвиг кривой спроса, так и движение вдоль кривой спроса.

Q = 1,200,000 – 150,000 × P

Обратная функция спроса

150,000 × P = 1,200,000 – Q

P = (1,200,000 – Q) / 150,000

P = 8 – Q / 150,000

P = 8 – 2 × Q / 150,000 = 8 – Q / 75,000

Примеры и графики

Сценарий А

Следующее уравнение показывает требуемое количество, соответствующее каждой цене:

Q_1.50 = 1,200,000 – 150,000 × $ 1.50 = 975,000

Q_1.75 = 1,200,000 – 150,000 × $ 1.75 = 937,500

Сценарий В

В этом случае происходит изменение цены заменителя, поэтому она представляет собой сдвиг кривой:

Q_1.50;0.25 = 1,200,000 – 150,000 × $ 1.50 + 200,000 × $ 0.25 = 1,025,000

Спрос и предложение

Спрос: понятие, функция, график

Пример: Даша хочет яблок и у нее есть деньги на их покупку — это спрос. Даша идет в магазин и покупает 3 яблока, потому что она хочет купить именно 3 яблока и у нее достаточно денег на эту покупку — это величина (объем) спроса.

Различают следующие виды спроса:

индивидуальный спрос — отдельного конкретного покупателя;
общий (совокупный) спрос — всех покупателей имеющихся на рынке.

Функция спроса — закон зависимости величины спроса от различных факторов оказывающих на него влияние.

Кривая спроса — графическое выражение зависимости величины спроса на некоторый товар от цены на него.

В простейшем случае функция спроса представляет собой зависимость его величины от одного ценового фактора:

где: Q_D — величина спроса на данный товар;

P — цена на данный товар.

где: Q_D — величина спроса на данный товар;

P — цена на данный товар;

a — коэффициент задающий смещение начала линии по оси абсцисс (X);

b — коэффициент задающий угол наклона линии (отрицательное число).

где: Q_D — величина спроса на данный товар;

P_X — цена на данный товар;

P₁..P_n — цена на другие взаимосвязанные товары (заменители, дополнители);

I — доход покупателей;

E — ожидания покупателей относительно роста цен в будущем;

N — количество возможных покупателей в данном регионе;

T — вкусы и предпочтения покупателей (привычки, следование моде, традициям и пр.);

Таким образом, факторы влияющие на спрос:

Ценовой фактор спроса — цена на данный товар;
Неценовые факторы спроса:
- наличие взаимосвязанных товаров (заменителей, дополнителей);
- уровень доходов покупателей (их платежеспособность);
- количество покупателей в данном регионе;
- вкусы и предпочтения покупателей;
- ожидания покупателей (относительно роста цен, будущих потребностей и пр.);
- иные факторы.

Закон спроса

Закон спроса — при росте цены на товар, спрос на него снижается, при прочих неизменных факторах, и наоборот.

Математически закон спроса означает наличие между величиной спроса и ценой обратной зависимости.

С обывательской точки зрения закон спроса полностью логичен — чем ниже цена на товар, тем привлекательнее его покупка и тем большее количество единиц товара будет куплено.

Закон спроса имеет теоретическое обоснование. В его основе лежат следующие механизмы:

Эластичность спроса

Числовой показатель, отражающий степень подобного изменения — коэффициент эластичности спроса.

где: E_P D — эластичность спроса по цене;

P₁ — первоначальная цена на товар;

Q₁ — первоначальная величина спроса на товар;

P₂ — новая цена;

Q₂ — новая величина спроса;

ΔP — приращение цены;

ΔQ — приращение величины спроса;

P_ср. — средняя цены;

Q_ср. — средняя величина спроса.

где: dQ — дифференциал величины спроса;

dP — дифференциал цены;

P₁, Q₁ — значение цены и величины спроса в анализируемой точке.

Совершенно неэластичный спрос или абсолютная неэластичность (|E| = 0). При изменении цены величина спроса практически не меняется. Близкими примерами могут служить товары первой необходимости (хлеб, соль, лекарства). Но в реальности нет товаров с совершенно неэластичным спросом на них;
Неэластичный спрос (0 ГРАФИК

Предложение: понятие, функция, график

Предложение (англ. «Supply») — способность и готовность продавцов продать товар по данной цене.

Различают следующие виды предложения:

индивидуальное предложение — конкретного отдельного продавца;
общее (совокупное) предложение — всех продавцов присутствующих на рынке.

Упрощенно функция предложения представляет собой зависимость его величины от цены (ценового фактора):

где: Q_S — величина предложения на данный товар;

P — цена на данный товар.

где: Q_S — величина предложения на данный товар;

P — цена на данный товар;

c — коэффициент задающий смещение начала линии по оси абсцисс (X);

d — коэффициент задающий угол наклона линии.

Функция предложения, в ее более сложной форме учитывающей влияние и неценовых факторов, представлена ниже:

где: Q_S — величина предложения;

P_X — цена данного товара;

P₁..P_n — цены других взаимосвязанных товаров (заменителей, дополнителей);

R — наличие и характер производственных ресурсов;

K — применяемые технологии;

C — налоги и дотации;

X — природно-климатические условия;

В этом случае кривая предложения будет иметь форму дуги (хотя это опять же упрощение).

Таким образом, факторы влияющие на предложение:

Ценовой фактор — цена на данный товар;
Неценовые факторы:
- наличие товаров-дополнителей и товаров-заменителей;
- уровень развития технологий;
- количество и доступность необходимых ресурсов;
- природные условия;
- ожидания продавцов (производителей): социальные, политические, инфляционные;
- налоги и дотации;
- тип рынка и его емкость;
- прочие факторы.

Закон предложения

Закон предложения, также как и закон спроса, очень логичен. Естественно, что любой продавец (производитель) стремится подать свой товар по более высокой цене. Если уровень цен на рынке повышается — продавцам выгодно продавать больше, если снижается — нет.

Эластичность предложения

Числовой показатель, отражающий степень такого изменения — коэффициент эластичности предложения.

Виды эластичности предложения по цене:

абсолютно неэластичное предложение (|E| = 0). Изменение цены совершенно не влияет на величину предложения. Это возможно в краткосрочном периоде;
неэластичное предложение (0 Рыночное равновесие графически выражается пересечением графиков спроса (D) и предложения (S) в одной точке. Этой точке рыночного равновесия соответствуют: P_E — равновесная цена, и Q_E — равновесный объем.

Например: цена выше равновесной. Продавцам выгодно продавать товар по более высокой цене и предложение повышается, возникает избыток товаров. А покупатели будут недовольны ростом цены на товар. Вдобавок конкуренция высокая, предложение избыточно и продавцам, чтобы реализовать товар придется снизить цену, пока она не придет к равновесному значению. При этом снизится и объем предложения до равновесного объема.

Галяутдинов Р. Р. Обзорные лекции для подготовки к госэкзаменам по специальности «Экономика и управление на предприятии». 2012.

источники:

http://sprintinvest.ru/funkciya-sprosa-pryamaya-i-obratnaya-s-primerami-i-grafikami-dvizheniya-i-sdviga

http://galyautdinov.ru/post/spros-i-predlozhenie

Источник