Пусть
зависимость между аргументом х и функцией
у задана параметрически в виде двух
уравнений
где
t — вспомогательная переменная, называемая
параметром.
Найдем
производную у’х,
считая, что функции (21.1) имеют производные
и что функция х=x(t) имеет обратную t=φ(х).
По правилу дифференцирования обратной
функции
Функцию
у=ƒ(х), определяемую параметрическими
уравнениями (21.1), можно рассматривать
как сложную функцию у=y(t), где t=φ(х). По
правилу дифференцирования сложной
функции имеем: у’х=y’t•t’x.
С учетом равенства (21.2) получаем
Полученная
формула позволяет находить производную
у’х от
функции заданной параметрически, не
находя непосредственной зависимости
у от х.
<<
Пример 21.2
Пусть
Найти
у’х.
Решение:
Имеем x’t=3t2,
y’t=2t.
Следовательно, у’х=2t/t2,
т. е.
В
этом можно убедиться, найдя непосредственно
зависимость у от х.
Действительно,
Тогда
Отсюда
т.
е.
22. Логарифмическое дифференцирование
В
ряде случаев для нахождения производной
целесообразно заданную функцию сначала
прологарифмировать. А затем результат
продифференцировать. Такую операцию
называют логарифмическим
дифференцированием.
<<
Пример 22.1
Найти
производную функции
Решение:
Пользуясь формулой (22.1), получаем:
Отметим,
что запоминать формулу (22.1) необязательно,
легче запомнить суть логарифмического
дифференцирования.
Существуют
функции, производные которых находят
лишь логарифмическим дифференцированием.
К их числу относится так
называемая степенно-показательная
функция у=uv,
где u=u(x) и ν=ν(х) — заданные дифференцируемые
функции от х. Найдем производную этой
функции:

Сформулируем
правило запоминания формулы (22.1):
производная степенно-показательной
функции равна сумме производной
показательной функции, при условии
u=const, и производной степенной функции,
при условии ν=const.
§23. Производные высших порядков
|
Додати |
Математика |
23. Производные высших порядков
23.1. Производные высших порядков явно заданной функции
Производная
у’=ƒ'(х) функции у=ƒ(х) есть также функция
от х и называется производной
первого порядка.
Если
функция ƒ'(х) дифференцируема, то ее
производная называется производной
второго порядка и обозначается у»
Итак,
у»=(у’)’.
Производная
от производной второго порядка, если
она существует, называется производной
третьего порядка и
обозначается у'» (или ƒ'»(х)). Итак,
у'»=(y»)’
Производной
n-го порядка (или n-й производной) называется
производная от производной (n-1)
порядка:
y(n)=(y(n-1))¢ .
Производные
порядка выше первого называются
производными высших порядков.
Начиная
с производной четвертого порядка,
производные обозначают римскими цифрами
или числами в скобках (уν или
у(5)—
производная пятого порядка).
<<
Пример 23.1
Найти
производную 13-го порядка функции у=sinx.
Решение:
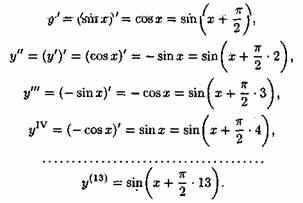
23.2. Механический смысл производной второго порядка
Пусть
материальная точка М движется прямолинейно
по закону S=f(t). Как уже известно, производная
S¢ t равна
скорости точки в данный момент времени:
S’t=V.
Покажем, что
вторая производная от пути по времени
есть величина, ускорения прямолинейного
движения точки, т.
е. S»=α.
Пусть
в момент времени t скорость точки равна
V, а в момент t+∆t — скорость равна V+∆V,
т. е. за промежуток времени ∆t скорость
изменилась на величину ∆V.
Отношение
∆V/∆t выражает среднее ускорение движения
точки за время ∆t. Предел этого отношения
при ∆t→0 называется ускорением точки
М в данный момент t и обозначается буквой
α:
Но
V=S’t.
Поэтому α=(S’t)’,
т. е. α=S’t‘
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Производная функции, заданной параметрически
4 января 2022
Сегодня мы научимся считать производную параметрической функции. Для этого разберём основную формулу, несколько примеров, но главное — одну из самых частых и глупых ошибок, которые допускают начинающие студенты.
План такой:
- Параметрическое задание функции — основные понятия
- Производная функции, заданной параметрически
- Типичные ошибки на примере второй производной
- Третья производная — разминка для мозгов
Начнём с ключевых определений и соображений.
1. Функция, заданная параметрически
Считая производные, мы привыкли работать с функциями, заданными аналитически, т.е. формулой $y=fleft( x right)$. Подставляя в эту формулу разные значения $x$, мы легко находим значение $y$.
Несколько примеров таких функций:
- Квадратичная функция: $y={{x}^{2}}$. График — парабола.
- Показательная функция: $y={{text{e}}^{x}}$. Она же «экспонента».
- Тригонометрическая функция: $y=sin x$. График — синусоида.
Но что если величины $y$ и $x$ зависят не друг от друга, а от некой третьей переменной? Скажем, от параметра $t$?
Пример 1. Функция, заданная параметрически:
[left{ begin{align} & x=cos t \ & y=sin t \ end{align} right.]
Перебирая разные $tin mathbb{R}$, мы будем получать точки с координатами $left( x;y right)$, которые в итоге превратятся в график:
Да это же тригонометрическая окружность! Она задаётся уравнением ${{x}^{2}}+{{y}^{2}}=1$.
График такого уравнения не является функцией (если забыли почему, гляньте урок про графики уравнений с двумя переменными). Но его можно «составить» из графиков двух функций:
[begin{align} & {{y}_{1}}=sqrt{1-{{x}^{2}}} \ & {{y}_{2}}=-sqrt{1-{{x}^{2}}} \ end{align}]
А вот это уже привычные нам аналитические функции, и для них можно посчитать производную!
К сожалению, далеко не всегда параметрическое уравнение вида
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
можно свести к привычными выражениям вида $y=fleft( x right)$. Но это ни в коем случае не означает, что для таких параметрических функций нельзя посчитать производную. Можно и даже нужно. И поможет нам в этом следующая формула.
2. Производная функции, заданной параметрически
Итак, основная теорема.
Теорема 1. Пусть функция $y=fleft( x right)$ задана параметрически:
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
Тогда производная этой функции считается по формуле
[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
Эту теорему очень легко доказать. В самом деле, если функция $x=varphi left( t right)$ рассматривается на интервале $tin left( a;b right)$ таком, что существует обратная функция $t={{varphi }^{-1}}left( x right)$, то можно определить сложную функцию
[yleft( x right)=psi left( {{varphi }^{-1}}left( x right) right)]
По теореме о производной сложной функции:
[{{{y}’}_{x}}left( x right)={{{psi }’}_{x}}left( {{varphi }^{-1}}left( x right) right)={{{psi }’}_{x}}left( t right)={{{psi }’}_{t}}left( t right)cdot {{{t}’}_{x}}left( x right)]
[begin{align} {{{{y}’}}_{x}}left( x right) & ={{{{psi }’}}_{x}}left( {{varphi }^{-1}}left( x right) right)= \ & ={{{{psi }’}}_{x}}left( t right)= \ & ={{{{psi }’}}_{t}}left( t right)cdot {{{{t}’}}_{x}}left( x right) end{align}]
Но по теореме об обратной функции ${{{t}’}_{x}}={1}/{{{{{x}’}}_{t}}};$, поэтому
[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
Что и требовалось доказать.
Замечание. Когда выражение дифференцируется по разным переменным, целесообразно указывать в нижним индексе ту переменную, по которой выполняется дифференцирование: ${{{y}’}_{x}}$, ${{{y}’}_{t}}$, ${{{x}’}_{t}}$ и т.д.
Это поможет избежать недоразумений и глупых вычислительных ошибок. Кроме того, подобные обозначения активно используются в дифференциальном исчислении функций нескольких переменных.
Детальное руководство по работе с нижними индексами и переменными дифференцирования — см. урок «Производная сложной функции». Сейчас просто отметим, что мы привыкли считать производную по переменной $x$. Но с тем же успехом можно считать производную и по $t$, и по какому-нибудь $varphi $, и вообще по любой переменной, которую мы увидим в функции.
2.1. Примеры
Приведённые выше формулы могут показаться сложными и страшными. Но на деле это одна из самых лёгких тем в производных. Взгляните:
Пример 1. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x=2t \ & y=3{{t}^{2}}-5t \ end{align} right.]
Считаем производные ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( 2t right)}^{prime }}_{t}=2 \ & {{{{y}’}}_{t}}={{left( 3{{t}^{2}}-5t right)}^{prime }}_{t}=6t-5 end{align}]
Теперь считаем ${{{y}’}_{x}}$ по формуле производной параметрической функции:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{6t-5}{2}]
Вот и всё! Готовое выражение можно разбить на две дроби, а можно оставить и так.
Пример 2. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x={{2}^{-t}} \ & y={{2}^{2t}} \ end{align} right.]
Вместо многочленов видим показательные функции. Это ничего не меняет, снова считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( {{2}^{-t}} right)}^{prime }}_{t}={{2}^{-t}}cdot left( -ln 2 right) \ & {{{{y}’}}_{t}}={{left( {{2}^{2t}} right)}^{prime }}_{t}={{2}^{2t}}cdot 2ln 2 end{align}]
Теперь находим ${{{y}’}_{x}}$ по формуле:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{2}^{2t}}cdot 2ln 2}{{{2}^{-t}}cdot left( -ln 2 right)}=-{{2}^{3t+1}}]
Для решения этого задания пришлось вспомнить производную показательной функции и некоторые свойства степеней.:)
Пример 3. Найдите ${{{y}’}_{x}}$, если
[left{ begin{align} & x=acos varphi \ & y=bsin varphi \ end{align} right.]
Здесь переменной-параметром является $varphi $, а буквы $a$ и $b$ — просто числа, которые будут частью ответа. Считаем ${{{x}’}_{varphi }}$ и ${{{y}’}_{varphi }}$ — производные тригонометрических функций:
[begin{align} & {{{{x}’}}_{varphi }}={{left( acos varphi right)}^{prime }}_{varphi }=-asin varphi\ & {{{{y}’}}_{varphi }}={{left( bsin varphi right)}^{prime }}_{varphi }=bcos varphiend{align}]
Находим ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{varphi }}}{{{{{x}’}}_{varphi }}}=frac{bcos varphi }{-asin varphi }=-frac{b}{a}operatorname{ctg}varphi ]
2.2. Производная в точке
Понятно, что это были совсем простые задачи. Буквально через минуту мы рассмотрим примеры посерьёзнее, но сначала важное дополнение.
Часто нам требуется посчитать не производную функции вообще, а лишь в конкретной точке. Например, чтобы провести касательную или нормаль к кривой, заданной параметрически, в некой точке ${{M}_{0}}left( {{x}_{0}};{{y}_{0}} right)$, лежащей на этой кривой.
В этом случае задача ещё более упрощается.
Пример 4. Найдите ${{{y}’}_{x}}$ при $t={pi }/{4};$, если
[begin{align} & xleft( t right)=tcdot left( tcos t-2sin t right) \ & yleft( t right)=tcdot left( tsin t+2cos t right) \ end{align}]
Задача явно серьёзнее, чем все предыдущие. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}=-left( {{t}^{2}}+2 right)cdot sin t \ & {{{{y}’}}_{t}}={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}=left( {{t}^{2}}+2 right)cdot cos t end{align}]
[begin{align} {{{{x}’}}_{t}} & ={{left( tcdot left( tcos t-2sin t right) right)}^{prime }}_{t}= \ & =-left( {{t}^{2}}+2 right)cdot sin t \ {{{{y}’}}_{t}} & ={{left( tcdot left( tsin t+2cos t right) right)}^{prime }}_{t}= \ & =left( {{t}^{2}}+2 right)cdot cos tend{align}]
И сразу подставляем $t={pi }/{4};$:
[begin{align} & {{{{x}’}}_{t}}left( frac{pi }{4} right)=-left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} \ & {{{{y}’}}_{t}}left( frac{pi }{4} right)=left( frac{{{pi }^{2}}}{16}+2 right)cdot frac{sqrt{2}}{2} end{align}]
Осталось найти ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=-frac{32+{{pi }^{2}}}{32+{{pi }^{2}}}=-1]
Разумеется, можно было сначала найти общую формулу для ${{{y}’}_{x}}$, а уже затем подставить в неё $t={pi }/{4};$ — результат получится точно такой же.
3. Типичные ошибки при вычислении производных
А теперь, пожалуй, ключевой момент, связанный с дифференцированием параметрических функций. Ошибка, которую я сам допустил много лет назад.
Давайте ещё раз взглянем на функцию, заданную параметрически:
[left{ begin{align} & x=varphi left( t right) \ & y=psi left( t right) \ end{align} right.]
И на производную этой функции:
[{{{y}’}_{x}}left( x right)=frac{{{{{y}’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
А теперь представьте, что надо посчитать вторую производную: ${{{y}»}_{xx}}$. И тут у многих проскакивает мысль: а что если взять формулу для первой производной и просто увеличить в ней количество «штрихов»?
Получится что-то типа вот этого:
[{{{y}»}_{xx}}left( x right)=frac{{{{{y}»}}_{tt}}left( t right)}{{{{{x}»}}_{tt}}left( t right)}]
Так вот: эта формула не верна!
Чтобы правильно найти вторую производную функции, заданной параметрически, достаточно вспомнить, что вторая производная — это просто производная от производной:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}]
Проще говоря, сначала мы находим ${{{y}’}_{x}}$ — это будет какая-то функция от $t$. Затем уже от этой функции вновь считаем производную — всё по той же формуле, которую мы сегодня уже много раз использовали. Получится так:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}]
Тут нас ждёт две новости:
- Хорошая: мы уже знаем ${{{x}’}_{t}}$. Это значит, что каждая последующая производная будет считаться чуть проще и быстрее;
- Плохая: можно легко запутаться во всех этих штрихах и переменных.
Чтобы разобраться с плохой новостью, достаточно просто небольшой практики. Поэтому сейчас мы разберём три примера. А точнее, три задачи из контрольных работ МГТУ им. Баумана. А там знают толк в производных.:)
Пример 5. Найдите ${{{y}»}_{xx}}$, если
[left{ begin{align} & x=cos 2t \ & y=sin t \ end{align} right.]
1. Сначала находим первую производную. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}=-2sin 2t=-4sin tcos t \ & {{{{y}’}}_{t}}=cos t end{align}]
Откуда находим саму производную ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{cos t}{-4sin tcos t}=-frac{1}{4sin t}]
2. Теперь находим вторую производную. Для этого считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -frac{1}{4sin t} right)}^{prime }}_{t}=frac{cos t}{4{{sin }^{2}}t}]
Кроме того, мы уже знаем ${{{x}’}_{t}}$. Поэтому находим вторую производную ${{{y}»}_{xx}}$:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}=-frac{1}{16}cdot frac{1}{{{sin }^{3}}t}]
[begin{align} {{{{y}»}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{cos t}{4{{sin }^{2}}t}cdot frac{1}{-4sin tcos t}= \ & =-frac{1}{16}cdot frac{1}{{{sin }^{3}}t} end{align}]
Вторая производная найдена.
Для сравнения посчитаем «производную» по неправильной формуле:
[frac{{{{{y}»}}_{tt}}}{{{{{x}»}}_{tt}}}=frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}=frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t}]
[begin{align} frac{{{{{y}»}}_{tt}}}{{{{{x}»}}_{tt}}} & =frac{{{left( {{{{y}’}}_{t}} right)}^{prime }}_{t}}{{{left( {{{{x}’}}_{t}} right)}^{prime }}_{t}}=frac{{{left( cos t right)}^{prime }}_{t}}{{{left( -2sin 2t right)}^{prime }}_{t}}= \ & =frac{-sin t}{-4cos 2t}=frac{1}{4}cdot frac{sin t}{cos 2t} end{align}]
Получили совершенно другое выражение, которое не является второй производной.
Итак, вторая производная считается из первой ровно по той же формуле, по какой первая производная считается из исходной функции.
Пример 6. Найдите ${{{y}»}_{xx}}$, если
[left{ begin{align} & x={{text{e}}^{t}}+1 \ & y=left( {{t}^{2}}-2t+2 right)cdot {{text{e}}^{t}} \ end{align} right.]
Первая производная ${{{y}’}_{x}}$ через ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{text{e}}^{t}} \ & {{{{y}’}}_{t}}={{t}^{2}}cdot {{text{e}}^{t}} \ & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ end{align}]
Вторая производная ${{{y}»}_{xx}}$ через ${{{x}’}_{t}}$ и ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[begin{align} & {{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=2t \ & {{{{y}»}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]
Замечание. Когда освоитесь с основной формулой, выкладки можно сократить буквально до двух строк:
[begin{align} & {{{{y}’}}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{{{t}^{2}}cdot {{text{e}}^{t}}}{{{text{e}}^{t}}}={{t}^{2}} \ & {{{{y}»}}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{2t}{{{text{e}}^{t}}} \ end{align}]
Впрочем, не стоит увлекаться сокращением выкладок, если у вас есть хоть малейшее сомнение или недопонимание на любом этапе вычислений.
Пара дополнительных минут — сомнительная экономия по сравнению с парой баллов на контрольной. И уж тем более по сравнению с недопониманием материала.
Пример 7. Найдите ${{{y}»}_{xx}}$, если
[left{ begin{align} & x={1}/{left( 1+{{t}^{2}} right)}; \ & y=2operatorname{arctg}t \ end{align} right.]
Дифференцирование арктангенса дробно-рациональной функции — довольно громоздкие действия. Тут в пару строк не уложиться.
1. Считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} & {{{{x}’}}_{t}}={{left( frac{1}{1+{{t}^{2}}} right)}^{prime }}_{t}=frac{-2t}{{{left( 1+{{t}^{2}} right)}^{2}}} \ & {{{{y}’}}_{t}}={{left( 2operatorname{arctg}t right)}^{prime }}_{t}=frac{2}{1+{{t}^{2}}} \ end{align}]
Первая производная ${{{y}’}_{x}}$:
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{2}{1+{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=-frac{1+{{t}^{2}}}{t}]
2. Считаем ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}=-frac{2tcdot t-left( 1+{{t}^{2}} right)}{{{t}^{2}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}]
Вторая производная ${{{y}»}_{xx}}$:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}=frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}}]
[begin{align} {{{{y}»}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =frac{1-{{t}^{2}}}{{{t}^{2}}}cdot frac{{{left( 1+{{t}^{2}} right)}^{2}}}{-2t}= \ & =frac{{{left( 1+{{t}^{2}} right)}^{2}}left( {{t}^{2}}-1 right)}{2{{t}^{3}}} end{align}]
Замечание. При делении дробных выражений полезно заменять их умножением на обратное:
[frac{Aleft( x right)}{Bleft( x right)}:frac{Pleft( x right)}{Qleft( x right)}=frac{Aleft( x right)}{Bleft( x right)}cdot frac{Qleft( x right)}{Pleft( x right)}]
Именно так мы и поступили при вычислении ${{{y}’}_{x}}$ и ${{{y}»}_{xx}}$ в последнем примере. И не только в последнем.:)
4. Третья производная
Пример 8. Найдите производную третьего порядка ${{{y}»’}_{xxx}}$ для функции, заданной параметрически:
[left{ begin{align} & xleft( t right)={{text{e}}^{t}}left( cos t+sin t right) \ & yleft( t right)={{text{e}}^{t}}left( cos t-sin t right) \ end{align} right.]
Решение будет состоять из трёх шагов.
1. Найдём первую производную ${{{y}’}_{x}}$. Для этого считаем ${{{x}’}_{t}}$ и ${{{y}’}_{t}}$:
[begin{align} {{{{x}’}}_{t}} & =2cos tcdot {{text{e}}^{t}} \ {{{{y}’}}_{t}} & =-2sin tcdot {{text{e}}^{t}} \ end{align}]
Первая производная ${{{y}’}_{t}}$ равна
[{{{y}’}_{x}}=frac{{{{{y}’}}_{t}}}{{{{{x}’}}_{t}}}=frac{-2sin tcdot {{text{e}}^{t}}}{2cos tcdot {{text{e}}^{t}}}=-operatorname{tg}t]
2. Считаем вторую производную. При этом ${{{x}’}_{t}}$ уже посчитано, осталось найти ${{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}$:
[{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}={{left( -operatorname{tg}t right)}^{prime }}_{t}=-frac{1}{{{cos }^{2}}t}]
Находим вторую производную по всё той же формуле:
[{{{y}»}_{xx}}={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}=-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t}]
[begin{align} {{{{y}»}}_{xx}} & ={{left( {{{{y}’}}_{x}} right)}^{prime }}_{x}=frac{{{left( {{{{y}’}}_{x}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}= \ & =-frac{1}{{{cos }^{2}}t}cdot frac{1}{2cos tcdot {{text{e}}^{t}}}= \ & =-frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} end{align}]
3. Считаем третью производную. Вновь нужно лишь найти ${{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}$:
[{{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}=frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t}]
[begin{align} {{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t} & ={{left( -frac{1}{2{{text{e}}^{t}}{{cos }^{3}}t} right)}^{prime }}_{t}= \ & =frac{cos t-3sin t}{2{{text{e}}^{t}}{{cos }^{4}}t} end{align}]
Для сокращения вычислений я сразу записал готовую формулу ${{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}$ — проверьте её самостоятельно. А дальше вновь используем формулу производной для параметрической функции:
[{{{y}»’}_{xxx}}=frac{{{left( {{{{y}»}}_{xx}} right)}^{prime }}_{t}}{{{{{x}’}}_{t}}}=frac{cos t-3sin t}{4{{text{e}}^{2t}}cdot {{cos }^{5}}t}]
Задача решена. Хотя вычислений получилось довольно много.
В любом случае помните главную формулу:
[{{{y}’}_{x}}left( x right)=frac{{{{{psi }’}}_{t}}left( t right)}{{{{{x}’}}_{t}}left( t right)}]
И помните, что вторая производная не равна частному вторых производных:
[{{{y}»}_{xx}}left( x right)ne frac{{{{{psi }»}}_{tt}}left( t right)}{{{{{x}»}}_{tt}}left( t right)}]
Попытка использовать эту формулу для нахождения производных высших порядков будет считаться грубой ошибкой.
Вот и вся теория. Теперь — за практику!:)
Смотрите также:
- Частные производные для функции нескольких переменных
- Формула полной вероятности
- Тест по теории вероятностей (1 вариант)
- Видеоурок по задачам C2: уравнение плоскости через определитель
- Процент: неизвестно начальное значение (метод пропорции)
- Производительность совместного труда
Параметрическое задание функции
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Параметрический способ задания функций
Пусть даны два уравнения
$x=phi (t)$ и $y=psi (t)$
В которых $t$ принимает значения с отрезка [n1; n2]. Каждому значению t соответствуют значения x и y — координаты точки на плоскости Оxy.
Когда $t$ изменяет свое значение на промежутке от $n1$ до $n2$, точка описывает некоторую кривую. Уравнения $x=phi (t)$ и $y=psi (t)$ получили название параметрических для кривой, а $t$ — параметра.
Предположим, что функция $x=phi (t)$ имеет обратную функцию $t= (x)$. Тогда справедливо равенство:
Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:
Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 1
Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.
Решение.
Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:
$x = v_0 t$
А вертикальное перемещение:
[s=frac{gt^{2} }{2} ]
Следовательно, расстояние от груза до земли в произвольный момент падения:
[y=y_{0} -frac{gt^{2} }{2} ]
Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.
[t=frac{x}{v_{0} } ]
Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:
[y=y_{0} -frac{g}{2v_{0}^{2} } x^{2} ]
Откуда:
[x=v_{0} sqrt{frac{2y_{0} }{g} } ]
«Параметрическое задание функции» 👇
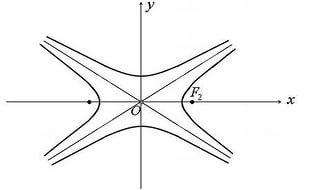
Уравнения некоторых кривых в параметрической форме:
- Окружность
- Гипербола
Уравнение окружности имеет вид:
[x^{2} +y^{2} =r^{2} ]
Параметрические кривые окружности:
[begin{array}{l} {x=rcos t} \ {y=rsin t} end{array}]
Рисунок 1. Окружность и ее параметрические кривые
Уравнение гиперболы имеет вид:
[frac{x^{2} }{a^{2} } -frac{y^{2} }{b^{2} } =1]
Параметрические кривые гиперболы:
[begin{array}{l} {left|xright|=acdot cht} \ {y=bcdot cht} end{array}]
Рисунок 2. Гипербола и ее параметрические кривые
Пример 2
Записать уравнение окружности в параметрическом виде.
[x^{2} +y^{2} =36]
Решение.
- Представим уравнение окружности в виде:
- Параметрические кривые окружности:
[x^{2} +y^{2} =r^{2} ]
[x^{2} +y^{2} =6^{2} ]
Значит, радиус $r$ равен 6.
[begin{array}{l} {x=rcos t} \ {y=rsin t} end{array}]
[begin{array}{l} {x=6cos t} \ {y=6sin t} end{array}]
Пример 3
Записать уравнение гиперболы в параметрическом виде.
[frac{x^{2} }{25} -frac{y^{2} }{9} =1]
Решение.
- Представим уравнение гиперболы в виде:
- Параметрические кривые гиперболы:
[frac{x^{2} }{5^{2} } -frac{y^{2} }{3^{2} } =1]
[begin{array}{l} {left|xright|=5cdot cht} \ {y=3cdot cht} end{array}]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 11.12.2022
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
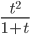
cos2(t) ≡ cos(t)^2
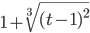
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
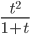
cos2(t) ≡ cos(t)^2
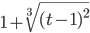
Пример 1. Найти производную функции y по x, заданной параметрически:
Решение.


Пример 2. Найти y’’xx функции
Решение. Найдем y’x по формуле (*): 
Производную y’x запишем в параметрической форме
К этой функции снова применим формулу (*):

Пример 3. Для функции 
Решение. 




Рассмотрим вопрос о дифференцировании функций, заданных параметрическим путем. До этого мы имели дело с функциями вида y=f(x)y=f(x) (то есть с явной зависимостью) и неявными функциями F(x,y)=0F(x, y)=0. Однако это не единственные способы представления функциональной зависимости между двумя величинами yy и xx.
Речь идет о функциях, которые задаются неким параметром tt. Идея состоит в том, что мы рассматриваем две «обычные» функции x=φ(t)x=varphi (t) и y=ψ(t)y=psi (t). Здесь видно, что каждому значению аргумента (параметра) tt будут отвечать какие-то частные значения функций φ(t)varphi (t) и ψ(t)psi (t). То есть для каждого значения tt мы получим два значения: xx и yy. А теперь смотрите: мы можем забыть, что у нас есть параметр tt, а довольствоваться только парой величин xx и yy.
Можно увидеть здесь функциональную зависимость между xx и yy и даже попытаться представить эту зависимость в привычном нам виде y=f(x)y=f(x). Следующие примеры помогут уяснить эту идею.
Примеры параметрически заданных функций
x=φ(t)=tx=varphi (t)=t,
y=ψ(t)=t2y=psi (t)=t^2
Это элементарный пример. Функция φ(t)varphi (t) имеет обратную, и мы легко можем выразить tt через xx. Здесь эти функции попросту совпадают и t=xt=x. Подставим теперь это выражение в функцию y=ψ(t)y=psi (t):
y=ψ(t)=t2=x2y=psi (t)=t^2=x^2
Вот мы и получили обычную функцию y=f(x)=x2y=f(x)=x^2. Дифференцировать такие функции мы, конечно, умеем. Здесь это просто f′(x)=2xf'(x)=2x.
x=φ(t)=t4x=varphi (t)=t^4,
y=ψ(t)=sinty=psi (t)=sin t
Чтобы представить данную функцию в обычном виде, нам нужно избавится от tt. То есть выразить его из одной функции и подставить в другую. В нашем случае tt проще выразить из первой функции. Получаем t=x14t=x^{frac{1}{4}}. Теперь подставим это в функцию для yy:
y=sint=sin(x14)y=sin t=sin big({x^{frac{1}{4}}}big)
x=φ(t)=a(t−sint)x=varphi (t)=a(t-sin t),
y=ψ(t)=a(1−cost)y=psi (t)=a(1-cos t),
−∞<t<∞-infty<t<infty
Если мы начертим кривую, задаваемую этими уравнениями (функциями), то получим удивительное изображение циклоиды. Ранее мы имели дело с такими параметрически заданными функциями, где без труда можно было избавиться от tt. Но бывают случаи, когда это сделать довольно непросто, а порой даже невозможно. В таком случае мы не сможем записать нашу функцию в виде y=f(x)y=f(x) и взять производную по тем правилам, которые мы уже знаем. Этот пример, впрочем, позволяет исключить tt. Можно пытаться выразить tt через yy из второго уравнения. Получается что-то вроде арккосинуса. Подставив tt в первое уравнение, мы получим функцию зависимости xx от yy. Но, возможно, нам захочется получить функцию yy от аргумента xx, а с этим могут возникнуть проблемы. А потом нужно будет это еще продифференцировать.
Так что все выглядит не очень просто. К счастью, математики на этот счет придумали способ, как можно вычислить производную от yy по xx, не получая предварительно функциональной зависимости вида y=f(x)y=f(x). Этим мы сейчас и займемся.
Дифференцирование параметрически заданной функции
Итак, представим себе, что xx и yy заданы как функции некого параметра tt:
x=φ(t)x=varphi (t),
y=ψ(t)y=psi (t).
Предположим также, что функции φ(t)varphi (t) и ψ(t)psi (t) нужное число раз дифференцируемые, то есть имеют нужное число производных по аргументу (параметру) tt. Наложим еще одно условие: чтобы у функции x=φ(t)x=varphi (t) существовала обратная функция t=φ−1(x)t=varphi^{-1}(x). Это значит, что первая производная φ′(t)varphi ‘(t) отлична от нуля.
Найдем теперь первую производную от yy по xx. Как вы помните, из определения производной следует, что:
yx′=dydx.y’_x=frac{dy}{dx}.
Запишем теперь аналогично первые производные от функций φ(t)varphi (t) и ψ(t)psi (t) по tt:
x′(t)=φ′(t)=dxdt,x'(t)=varphi ‘(t)=frac{dx}{dt},
y′(t)=ψ′(t)=dydt.y'(t)=psi ‘(t)=frac{dy}{dt}.
Теперь выразим дифференциалы dxdx и dydy: dx=φ′(t)dtdx=varphi ‘(t)dt и dy=ψ′(t)dtdy=psi ‘(t)dt. Наконец, подставим их в определение первой производной функции y(x)y(x):
yx′=dydx=ψ′(t)dtφ′(t)dt=ψ′(t)φ′(t).y’_x=frac{dy}{dx}=frac{psi ‘(t)dt}{varphi ‘(t)dt}=frac{psi ‘(t)}{varphi ‘(t)}.
Вот это и есть главное правило дифференцирования параметрически заданных функций. Сформулируем его так:
Если нам даны функции x=φ(t)x=varphi (t) и y=ψ(t)y=psi (t) параметра tt, то производная от функции yy по аргументу xx представляется выше приведенной формулой. Нужно просто производную ψ′(t)psi ‘(t) разделить на производную φ′(t)varphi ‘(t).
Теперь, кстати, понятно, почему мы потребовали, чтобы первая производная φ′(t)varphi ‘(t) была отлична от нуля. В противном случае у нас в знаменателе оказался бы нуль, а на нуль, как известно, делить очень трудно. Аналогичным образом можно подойти и к определению формул для производных функции y=f(x)y=f(x) высших порядков.
Теперь, вооружившись этой главной формулой, мы можем приступить к тем примерам, которые мы приводили раньше. Для двух первых случаев мы вычислим производные yx′y’_x двумя способами и сравним их. То есть сначала мы используем правило дифференцирования параметрически заданных функций, а потом воспользуемся явным видом функции y=f(x)y=f(x) там, где это возможно сделать.
x=φ(t)=tx=varphi (t)=t,
y=ψ(t)=t2y=psi (t)=t^2
x′(t)=φ′(t)=1x'(t)=varphi ‘(t)=1
y′(t)=ψ′(t)=2ty'(t)=psi’ (t)=2t
yx′=ψ′(t)φ′(t)=2ty’_x=frac{psi’ (t)}{varphi ‘(t)}=2t
Для того чтобы получить эту производную как функцию xx, а не tt, нам нужно выразить tt через xx и подставить в формулу для производной. Вы можете сказать, зачем нам нужен этот новый способ дифференцирования параметрически заданных функций, если нам все равно приходится выражать tt через xx. Но здесь это нужно сделать только для того, чтобы получить результат дифференцирования, то есть производную, как функцию xx. Саму же производную (пусть даже параметра tt) мы получили без какого бы то ни было выражения tt через xx. И уж точно мы не пытались записать функцию вида y=f(x)y=f(x). Так что разница все-таки есть.
Хорошо, tt легко выражается через xx: t=xt=x. Значит: yx′=2t=2xy’_x=2t=2x.
Вычислим теперь эту производную, воспользовавшись явной функцией f(x)f(x). Раннее мы установили, что y=x2y=x^2 и f′(x)=2xf'(x)=2x. Это совпадение и доказывает, что мы все делаем правильно.
x=φ(t)=t4x=varphi (t)=t^4,
y=ψ(t)=sinty=psi (t)=sin t
t=x14t=x^{frac{1}{4}}
y=sint=sin(x14)y=sin t=sin big({x^{frac{1}{4}}}big)
x′(t)=φ′(t)=4t3x'(t)=varphi ‘(t)=4t^3
y′(t)=ψ′(t)=costy'(t)=psi’ (t)=cos t
yx′=ψ′(t)φ′(t)=14costt3y’_x=frac{psi’ (t)}{varphi ‘(t)}=frac{1}{4}frac{cos t}{t^3}
Подставим теперь сюда tt как функцию xx:
yx′=14cos(x14)x34y’_x=frac{1}{4}frac{cos big(x^{frac{1}{4}}big)}{x^frac{3}{4}}
Теперь вычислим производную y′(x)y'(x) прямо:
y′(x)=ddxsin(x14)=cos(x14)ddxx14=14cos(x14)x34y'(x)=frac{d}{dx}sin big({x^{frac{1}{4}}}big)=cos (x^frac{1}{4})frac{d}{dx}x^{frac{1}{4}}=frac{1}{4}frac{cos big(x^frac{1}{4}big)}{x^frac{3}{4}}
Отлично, опять совпадение.
x=φ(t)=a(t−sint)x=varphi (t)=a(t-sin t),
y=ψ(t)=a(1−cost)y=psi (t)=a(1-cos t),
−∞<t<∞-infty<t<infty
Здесь мы вычислим производную только первым способом.
x′(t)=φ′(t)=a(1−cost)x'(t)=varphi ‘(t)=a(1-cos t)
y′(t)=ψ′(t)=asinty'(t)=psi’ (t)=asin t
yx′=asinta(1−cost)=ctgt2, t≠2πk, k∈Zy’_x=frac{asin t}{a(1-cos t)}=ctg frac{t}{2}, tneq 2pi k, k in Z