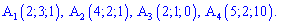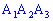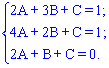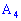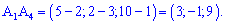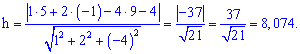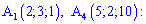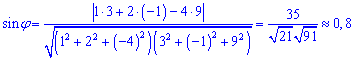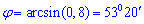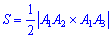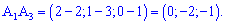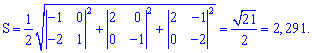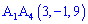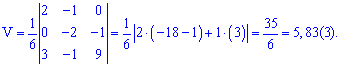Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
|
|
 |
|
||||
| Теги: уравнение плоскости через данную точку перпендикулярно данному вектору, векторное произведение |
Лучший ответ
|
|
 |
|
Другие ответы
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
Пример 1:
Решение от преподавателя:
3) Для нахождения уравнения плоскости, содержащей грань SPN используем уравнение плоскости, проходящей через три точки:
-4x -8y — z + 21 = 0 — уравнение грани А1А2А3
4) Площадь треугольника, построенного на векторах и
находится по формуле:
где

Грань SPN образована векторами .
Находим координаты векторов :
и площадь грани SPN:
5) Находим нормальный вектор плоскости PMN:
Высота (SН), опущенная из вершины S на грань PMN, перпендикулярна плоскости PMN, а значит направляющий вектор прямой SН параллелен вектору-нормали плоскости PMN, поэтому в качестве направляющего вектора прямой SН можно взять вектор-нормаль плоскости . Высота SН проходит через вершину S, поэтому можно записать каноническое уравнение высоты:
6) Плоскость PMN имеет нормальный вектор и проходит через точку М(0,0,2), поэтому уравнение этой плоскости имеет вид:
Длину высоты SH находим как расстояние от точки S для плоскости PMN:
7) Находим угол между ребрами SP и SN:

(см. п.6):
9) Объем пирамиды, построенной на векторах и
находится по формуле:
где

Пирамида SPMN образована векторами .
Находим координаты векторов
и объем пирамиды:
Ответ:
Пример 2:
Решение от преподавателя:
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Аналитическая геометрия — задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Задача 1.
Тетраэдр в пространстве задано вершинами
Необходимо найти:
1) уравнение грани 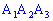
2) уравнение высоты пирамиды, которая проходит через вершину 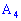
3) длину этой высоты;
4) угол между ребром 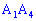
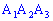
5) площадь грани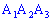
6) Объем пирамиды.
Решение.
1) Уравнение грани
Запишем уравнение плоскости в виде.
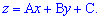
Поскольку все три точки принадлежат этой плоскости, то, подставляя их по очереди получим систему уравнений
Решая ее получим.
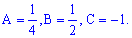
Подставляя в исходное уравнение получим
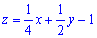
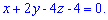
2) Уравнение высоты пирамиды, проходящей через вершину
Запишем уравнение высоты пирамиды, проходящей через вершину
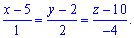
3) Высота с вершины
Найдем высоту, для этого найдем
Высоту найдем учитывая уравнение грани 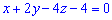
4)Угол между ребром 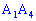
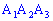
Найдем угол между ребром 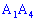
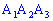
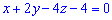
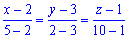
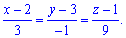
Найдем синус угла по формуле
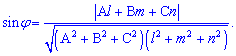
Подставим значения
Найдем значение угла
5) Площадь грани
Площадь грани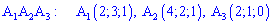
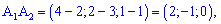
6) Объем пирамиды
Найдем объем пирамиды пирамиды по формуле
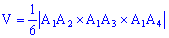
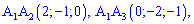
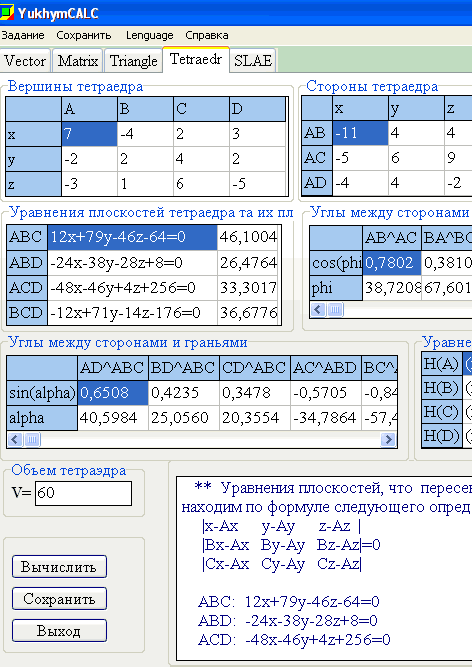
Математический калькулятор YukhymCalc решает эту задачу и немало типичных для студенческой практики математических задач. Фрагмент работы калькулятора приведены ниже.
——————————
Посмотреть материалы:
- Длина вектора. Угол между векторами
- Разложение вектора по базису
- Проекция вектора на вектор
- Смешанное произведение векторов
- Деление отрезка в заданном отношении