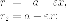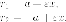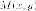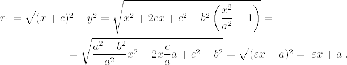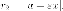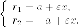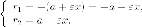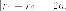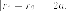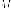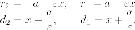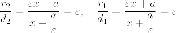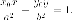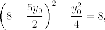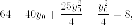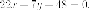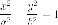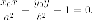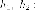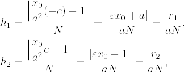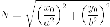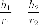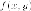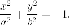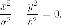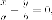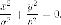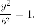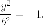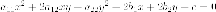-
Гипербола и её форма.
Начать изучение
-
Фокусы, эксцентриситет и директрисы гиперболы.
Начать изучение
-
Точки гиперболы и их свойства.
Начать изучение
-
Уравнение касательной к гиперболе.
Начать изучение
Гипербола и её форма.
Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9}
$$
Из этого уравнения видно, что для всех точек гиперболы (|x| geq a), то есть все точки гиперболы лежат вне вертикальной полосы ширины (2a) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами ((a, 0)) и ((-a, 0)), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа (a) и (b) называются соответственно вещественной и мнимой полуосями гиперболы.
Утверждение.
Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.
Доказательство.
Доказательство аналогично доказательству соответствующего утверждения для эллипса.
Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде (y=kx), поскольку мы уже знаем, что прямая (x=0) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1.
$$
Поэтому, если (b^{2}-a^{2}k^{2} > 0), то
$$
x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}}.
$$
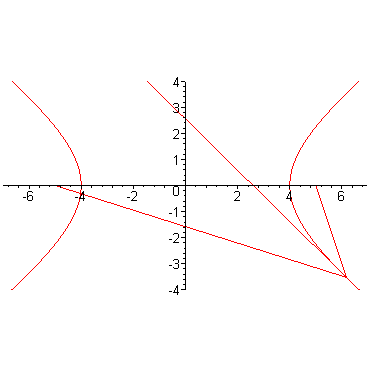
Это позволяет указать координаты точек пересечения ((ab/v, abk/v)) и ((-ab/v, -abk/v)), где обозначено (v=(b^{2}-a^{2}k^{2})^{1/2}). В силу симметрии достаточно проследить за движением первой из точек при изменении (k) (рис. 8.7).
Числитель дроби (ab/v) постоянен, а знаменатель принимает наибольшее значение при (k=0). Следовательно, наименьшую абсциссу имеет вершина ((a, 0)). С ростом (k) знаменатель убывает, и (x) растет, стремясь к бесконечности, когда (k) приближается к числу (b/a). Прямая (y=bx/a) с угловым коэффициентом (b/a) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.
Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то (k) будет убывать, (k^{2}) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом (-b/a).
К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.
Определение.
Прямые с уравнениями (y=bx/a) и (y=-bx/a) в канонической системе координат называются асимптотами гиперболы.
Запишем уравнения асимптот в виде (bx-ay=0) и (bx+ay=0). Расстояния от точки (M(x, y)) до асимптот равны соответственно
$$
h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}}, h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}}.nonumber
$$
Если точка (M) находится на гиперболе, то (b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}), и
$$
h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}}.nonumber
$$
Утверждение.
Произведение расстояний от точки гиперболы до асимптот постоянно и равно (a^{2}b^{2}/(a^{2}+b^{2})).
Отсюда следует важное свойство асимптот.
Свойство.
Если точка движется по гиперболе так, что ее абсцисса по абсолютной величине неограниченно возрастает, то расстояние от точки до одной из асимптот стремится к нулю.
Доказательство.
Действительно, хотя бы одно из расстояний (h_{1}) или (h_{2}) при этих условиях должно неограниченно возрастать, и, если бы предложение было неверно, произведение не было бы постоянно.
Фокусы, эксцентриситет и директрисы гиперболы.
Определение.
Введем число (c), положив
$$
c^{2}=a^{2}+b^{2}label{ref10}
$$
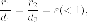
и (c > 0). Фокусами гиперболы называются точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.
Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).
Утверждение 9.
Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов следующим образом зависят от ее абсциссы (x):
$$
r_{1}=|F_{1}M|=|a-varepsilon x|, r_{2}=|F_{2}M|=|a+varepsilon x|.label{ref11}
$$
Доказательство.
Доказательство этого утверждения почти дословно совпадает с доказательством аналогичного утверждения для эллипса.
Заметим, что равенства eqref{ref11} можно подробнее записать так:
- для правой ветви гиперболы ((x geq a))
$$
r_{1}=varepsilon x-a, r_{2}=varepsilon x+a;nonumber
$$ - для левой ветви гиперболы ((x leq -a))
$$
r_{1}= a-varepsilon x, r_{2}=-varepsilon x-a;nonumber
$$
Итак, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях
$$
|r_{2}-r_{1}|=2a.label{ref12}
$$
Директрисами гиперболы называются прямые, задаваемые в канонической системе координат уравнениями
$$
x=frac{a}{varepsilon}, x=-frac{a}{varepsilon}.label{ref13}
$$
Директрисы лежат ближе к центру, чем вершины, и, следовательно, не пересекают гиперболу. Директриса и фокус, лежащие по одну сторону от центра, считаются соответствующими друг другу.
Точки гиперболы и их свойства.
Утверждение 10.
Для того чтобы точка (M) лежала на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы (2a).
Доказательство.
Необходимость условия уже доказана. Для доказательства достаточности условия его нужно представить в виде
$$
sqrt{(x-c)^{2}+y^{2}}=pm 2a+sqrt{(x+c)^{2}+y^{2}}nonumber
$$
Дальнейшее отличается от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством (c^{2}=a^{2}+b^{2}), а не (c^{2}=a^{2}-b^{2}).
Утверждение 11.
Для того чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету (varepsilon) (рис. 8.10).
Доказательство.
Доказательство повторяет доказательство предложения 4. Докажем, например, необходимость условия для фокуса (F_{2}(-c, 0)). Пусть (M'(x, y)) — точка гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) по формуле (9) § 3 гл. II равно
$$
d’=left|x+frac{a}{varepsilon}right|=frac{1}{varepsilon}|varepsilon x+a|.nonumber
$$
Из формулы eqref{ref11} мы видим теперь, что (r’/d’=varepsilon).
Уравнение касательной к гиперболе.
Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), лежащей на ней, выводится так же, как соответствующее уравнение касательной для эллипса. Оно имеет вид
$$
frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1.label{ref14}
$$
Утверждение 12.
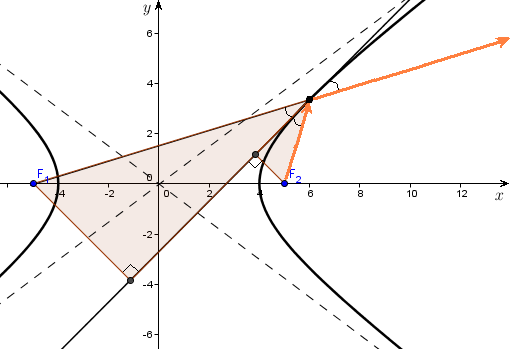
Касательная к гиперболе в точке (M_{0}(x_{0}, y_{0})) есть биссектриса угла между отрезками, соединяющими эту точку с фокусами.
Доказательство.
Доказательство почти не отличается от доказательства соответствующего утверждения для эллипса.
math-public:krivye-vtorogo-poryadka-giperbola
Содержание
Гипербола
Определение
Гипербола – это геометрическое место точек, модуль разности расстояний от которых до двух данных точек $F_1$ и $F_2$ постоянен и при этом меньше, чем $|F_1F_2|$.
Теорема
Каноническое уравнение гиперболы имеет вид $frac{x^2}{a^2}-frac{y^2}{b^2}=1$, число $a$ называется
вещественной полуосью гиперболы, $b$ – мнимой полуосью.
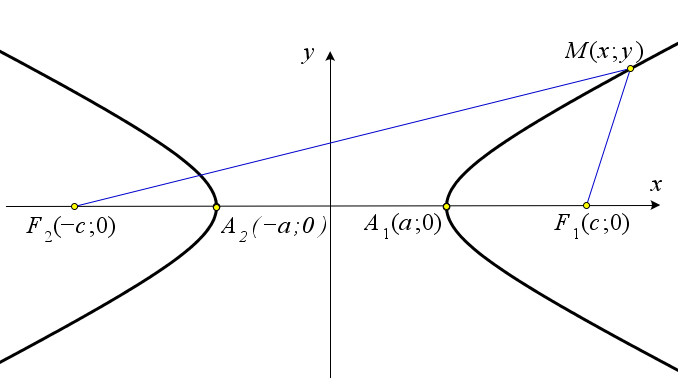
Доказательство
Пусть $M(x,y)$ – это произвольная точка, принадлежащая данной
гиперболе, а точки $F_1(c;0)$ и $F_2(-c;0)$ – это её фокусы (рис.
ref{pic159}).
Тогда по определению гиперболы $|MF_1-MF_2|$ постоянен.
Пусть этот модуль равен $2a$, то есть $|MF_1-MF_2|=2a$.
Распишем это равенство с помощью формулы расстояния между двумя точками:
$$|sqrt{(x-c)^2+y^2}-sqrt{(x+c)^2+y^2}|=2a$$
Возведём это равенство в квадрат, раскроем скобки и приведём подобные слагаемые:
$$2x^2+2c^2+2y^2-2sqrt{(x-c)^2+y^2}sqrt{(x+c)^2+y^2}=4a^2$$
или
$$sqrt{(x-c)^2+y^2}sqrt{(x+c)^2+y^2}=x^2+y^2+c^2-2a^2.$$
При условии, что $x^2+y^2+c^2-2a^2geqslant0$, данное уравнение можно
возвести в квадрат:
$$((x-c)^2+y^2)((x+c)^2+y^2)=4a^4-4a^2(x^2+y^2+c^2)+(x^2+y^2+c^2)^2$$
или
$$(x^2+c^2+y^2-2xc)(x^2+c^2+y^2+2xc)=4a^4-4a^2x^2-4a^2y^2-4a^2c^2+(x^2+y^2+c^2)^2.$$
В левой части раскроем скобки, используя формулу разности квадратов:
$$(x^2+y^2+c^2)^2-4x^2c^2=4a^4-2a^2x^2-2a^2y^2-2a^2c^2+(x^2+y^2+c^2)^2.$$
Сократив подобные слагаемые, перенеся все слагаемые в одну часть, и сократив на $4$, получим:
$$a^4-a^2x^2-a^2y^2-a^2c^2+x^2c^2=0.$$
Перегруппируем слагаемые:
$$(a^4-a^2c^2)+(x^2c^2-x^2a^2)-a^2y^2=0,$$
$$x^2(a^2-c^2)+a^2y^2=a^2(a^2-c^2).$$
Так как $a<c$, то можно разделить последнее равенство на $a^2(a^2-c^2)$:
$$frac{x^2}{a^2}+frac{y^2}{a^2-c^2}=1.$$
Обозначив $b^2=c^2-a^2$, получим
begin{equation}label{eq011}
frac{x^2}{a^2}-frac{y^2}{b^2}=1.
end{equation}
Теперь докажем, что любая пара чисел $(x,y)$, удовлетворяющая последнему равенству, удовлетворяет условию
$(x^2+y^2+c^2)-2a^2geqslant0$.
Преобразуем левую часть:
$$x^2+y^2+c^2-2a^2=x^2+y^2-a^2+(c^2-a^2)=x^2+y^2-a^2+b^2.$$
Из равенства ref{eq011} следует, что $x^2=a^2left(1+frac{y^2}{b^2}right)geqslant a^2$, так как
$1+frac{y^2}{b^2}geqslant 1$.
Следовательно, $x^2geqslant a^2$, а значит,
$$x^2+y^2-a^2+b^2geqslant y^2+b^2geqslant0$$
или
$$x^2+y^2-a^2+b^2geqslant 0.$$
Следовательно,
$$x^2+y^2+c^2-2a^2geqslant0.$$
Свойства канонической гиперболы
-
Вершины гиперболы имеют координаты $A_{1,2}(pm a;0)$.
-
Каноническая гипербола имеет две асимптоты с уравнениями $y=pmfrac{b}{a}x$.
-
Фокусы канонической гиперболы имеют координаты $F_1(c;0)$ и $F_2(-c;0)$, при этом $b^2=c^2-a^2$ и $c>a$.
-
Эксцентриситетом гиперболы называется число $e=frac{c}{a}$.
Теорема о касательной к гиперболе
Пусть точка $M(x_0;y_0)$ – произвольная точка гиперболы
$frac{x^2}{a^2}-frac{y^2}{b^2}=1$. Тогда уравнение касательной к
гиперболе, проведенной в этой точке имеет вид
$frac{xx_0}{a^2}-frac{yy_0}{b^2}=1$.
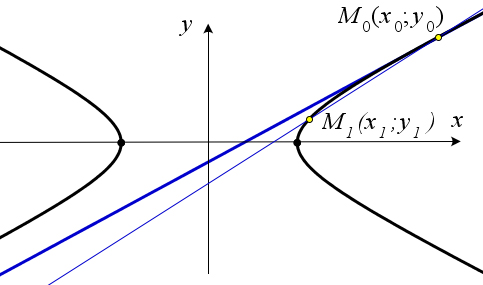
Доказательство
По определению касательной к кривой в данной токе $M$ называется предельное положение секущей $M_0M_1$ при условии, что точка $M_1$ стремится к точке $M_0$ по данной кривой.
Рассмотрим уравнение секущей к эллипсу, проходящей через точку $M_0(x_0;y_0)$ и не совпадающую с ней точку $M_1(x_1;y_1)$.
Поскольку точка $M_1$ стремится к точке $M_0$, знаки их абсцисс совпадают.
Рассмотрим случай, когда абсциссы точек $M_0$ и $M_1$ положительны.
Так как обе точки лежат на гиперболе $frac{x^2}{a^2}+frac{y^2}{b^2}=1$, то их координаты можно записать
в виде $M_0(frac{a}{b}sqrt{b^2+y_0^2};y_0), M_1(frac{a}{b}sqrt{b^2+y_1^2};y_1)$.
Запишем уравнение прямой $M_0M_1$:
$$frac{x-x_0}{x_0-x_1}=frac{y-y_0}{y_0-y_1},$$
$$frac{x-frac{a}{b}sqrt{b^2+y_0^2}}{frac{a}{b}sqrt{b^2+y_0^2}-frac{a}{b}sqrt{b^2+y_1^2}}=frac{y-y_0}{y_0-y_1},$$
$$frac{(frac{b}{a}x-sqrt{b^2+y_0^2})(sqrt{b^2+y_0^2}+sqrt{b^2+y_1^2})}{y_0^2-y_1^2}=frac{y-y_0}{y_0-y_1},$$
$$(frac{b}{a}x-sqrt{b^2+y_0^2})(sqrt{b^2-y_0^2}+sqrt{b^2-y_1^2})=(y-y_0)(y_0+y_1).$$
Если точка $M_1$ стремиться к точке $M_0$ по гиперболе, то $y_1$ стремиться к $y_0$.
Тогда последнее равенство можно записать в виде
$$(frac{b}{a}x-sqrt{b^2+y_0^2})cdot2sqrt{b^2+y_0^2}=(y-y_0)cdot2y_0,$$
$$frac{b}{a}xsqrt{b^2+y_0^2}-b^2-y_0^2=yy_0-y_0^2,$$
$$frac{b}{a}xsqrt{b^2+y_0^2}-yy_0=b^2.$$
Разделим это равенство на $b^2$:
$$frac{1}{ab}xsqrt{b^2+y_0^2}-frac{yy_0}{b^2}=1.$$
Учитывая, что $x_0=frac{a}{b}sqrt{b^2+y_0^2}$, получаем:
$$frac{x}{a^2}cdotfrac{a}{b}sqrt{b^2+y_0^2}-frac{yy_0}{b^2}=1,$$
$$frac{xx_0}{a^2}-frac{yy_0}{b^2}=1.$$
Случай, когда абсциссы точек $M_0$ и $M_1$ отрицательны рассматривается аналогично, с той лишь разницей, что теперь
координаты этих точек будут иметь вид $M_0(-frac{a}{b}sqrt{b^2+y_0^2};y_0), M_1(-frac{a}{b}sqrt{b^2+y_1^2};y_1)$.
Лемма
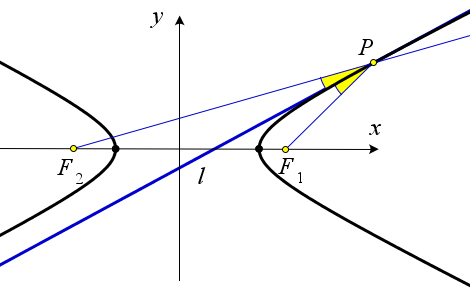
Максимум модуля разности расстояний от точки данной прямой $l$ до точек $F_1$ и $F_2$, лежащих по разные стороны от данной прямой достигается в такой точке $P$, для которой лучи $PF_1$ и $PF_2$ образуют равные углы с прямой $l$.
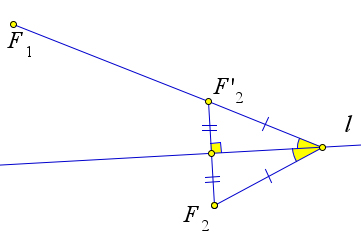
Доказательство
Обозначим через $F_2’$ точку, симметричную $F_2$ относительно прямой $l$.
Очевидно, что $F_2X=F_2’X$ для любой точки $X$ на прямой $l$.
Нам достаточно найти такую точку $P$, что разность расстояний от $P$ до $F_1$ и $F_2’$ будет как можно больше.
Из неравенства треугольника следует, что $|F_1P-F_2’P|<F_1F_2’$.
И достигается этот максимум тогда и только тогда, когда точки $F_1, F_2, P$ лежат на одной прямой.
Поскольку точки $F_2$ и $F_2’$ симметричны, углы, которые образуют прямые $F_1P$ и $F_2P$ с прямой
$l$, равны.
Оптическое свойство гиперболы
Луч света, вышедший из фокуса $F_2$, отразившись от какой-либо точки $M$ гиперболы, распространяется далее вдоль луча $F_1M$, то есть так, как если бы луч света исходил из фокуса $F_1$ и распространялся бы без помех.
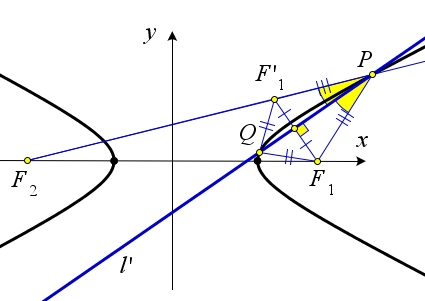
Доказательство
Переформулируем утверждение: если прямая $l$ касается гиперболы в точке $P$, то $l$ является биссектрисой угла $F_1PF_2$, где $F_1$ и $F_2$ – фокусы гиперболы.
Предположим, что биссектриса $l’$ угла $F_1PF_2$ пересекает гиперболу ещё в какой-нибудь точке $Q$ (лежащей на той же дуге, что и $P$).
Для удобства будем считать, что точка $P$ лежит на дуге, которая ближе к фокусу $F_1$.
Обозначим через $F_1’$ точку, симметричную $F_1$ относительно $l’$. Тогда $F_1Q=QF_1’$, $F_1P=PF_1’$;
кроме того, точки $F_2, F_1’$ и $P$ лежат на одной прямой.
Итак, $F_2P-PF_1=F_2Q-F_1Q$. В силу вышеуказанных равенств получаем $F_2F_1’=F_2P-PF_1’=F_2Q-QF_1’$.
Но по неравенству треугольника $F_2F_1′>F_2Q-QF_1’$.
Таким образом получено противоречие, что и доказывает утверждение теоремы.
· Последнее изменение: 2017/04/20 19:21 —
labreslav
Гипербола и её свойства
Гипербола и её форма.
Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac>>-frac>>=1.label
$$
Из этого уравнения видно, что для всех точек гиперболы (|x| geq a), то есть все точки гиперболы лежат вне вертикальной полосы ширины (2a) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами ((a, 0)) и ((-a, 0)), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа (a) и (b) называются соответственно вещественной и мнимой полуосями гиперболы.
Рис. 8.6. Гипербола.
Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.
Доказательство аналогично доказательству соответствующего утверждения для эллипса.
Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде (y=kx), поскольку мы уже знаем, что прямая (x=0) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
frac>>-fracx^<2>>>=1.
$$
Поэтому, если (b^<2>-a^<2>k^ <2>> 0), то
$$
x=pm frac<sqrt-a^<2>k^<2>>>.
$$
Это позволяет указать координаты точек пересечения ((ab/v, abk/v)) и ((-ab/v, -abk/v)), где обозначено (v=(b^<2>-a^<2>k^<2>)^<1/2>). В силу симметрии достаточно проследить за движением первой из точек при изменении (k) (рис. 8.7).
Рис. 8.7. Пересечение прямой и гиперболы.
Числитель дроби (ab/v) постоянен, а знаменатель принимает наибольшее значение при (k=0). Следовательно, наименьшую абсциссу имеет вершина ((a, 0)). С ростом (k) знаменатель убывает, и (x) растет, стремясь к бесконечности, когда (k) приближается к числу (b/a). Прямая (y=bx/a) с угловым коэффициентом (b/a) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.
Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то (k) будет убывать, (k^<2>) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом (-b/a).
К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.
Прямые с уравнениями (y=bx/a) и (y=-bx/a) в канонической системе координат называются асимптотами гиперболы.
Задача 36959 найти уравнение касательных к гиперболе.
Условие
найти уравнение касательных к гиперболе x^2/5-y^2/4=1 параллельных прямой x+y-4=0
Решение
x + y — 4 = 0 ⇒ y= — x + 4
Значит, касательные || прямой имеют вид
Прямая y=-x+b и гипербола y^2=(4/5)x^2 — 4
имеют одну общую точку, т. е
(4/5)x^2-4=(-x+b)^2 имеет единственное решение
Квадратное уравнение имеет один корень, если D=0
Оптическое свойство кривых второго порядка. Касательные к эллипсу и гиперболе
По этой ссылке вы найдёте полный курс лекций по математике:
Предположим для определенности, что точка М0 лежит в первой четверти, т. е. х0 > О, Уо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо а так как точка (я0, уо) лежит на эллипсе, то Пусть mq(xо, уо) — точка эллипса и, значит, Полученное соотношение после несложных преобразований можно записать так: Отсюда с учетом тождества приходим к уравнению.
Оптическое свойство кривых второго порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка (рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (я0, Уо), и в обшем случае ее произвольного расположения, т.е. прилюбыхзнаках яо и у0. .
Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид Подчеркнем, что точка (xq, Уо) лежит на гиперболе. Если кривая задана уравнением то уравнение касательной к ней, проходящей через точку (х0,у0), где уо = f(xо), можно записать в следующем виде Касательные к параболе Если кривая задана уравнением то уравнение касательной к ней, проходящей через точку (хо,2/о)> ГДе х0 = д(уо), можно записать в следующем виде Пусть Л/о(х0, уо) — точка параболы.
Пользуясь формулой (I), получаем уравнение касательной к параболе Отсюда в силу равенства yl = 2рх0 приходим к уравнению касательной вида Замечание. Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, чтодля получения последних не требуется специальных вычислений.
В самом деле, заменяя у2 на 3/3/0» а х2 на xxq (в случае параболы 2х нужно заменить на х + хо). приходим к уравнению соответствующей касательной. Еше раз отметим, что сказанное справедливо лишь в том случае, когда точка (го. Уо) лежит на кривой. 6.3. Оптическое свойство эллипса Пусть Мо — произвольная точка эллипса Как уже отмечалось, расстояния от нее до фокусов F„ и Fn — фокальные радиусы — равны соответственно.
Проведем через точку А/0 касательную к эллипсу, и вычислим, на каком расстоянии от этой касательной лежат фокусы Fn(
c, 0) и Fn(c, 0) (напомним, что для этого следует воспользоваться формулой (10) из §11.1). Имеем соответственно или — нормирующий м ножитель (рис. 29). Нетрудно проверить,что В самом деле, Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания.
Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания. Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник Рис.29 света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).
Оптическое свойство гиперболы Устанавливается аналогичными выкладками и заключается в следующем. Если поместить водин из фокусов гиперболы точечный источниксвета,то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31). Оптическое свойство параболы Если в фокус параболы помешен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис.32).
Многочлены второй степени на плоскости Теорема. Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть Оптическое свойство кривых второго порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка — многочлен второй степени от переменных х и у.
Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X uY исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов: шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль. Пусть 6^0 (при этот шаг не нужен).
Возможно вам будут полезны данные страницы:
Повернем оси координат вокругточки О. Эта операция описывается следующими формулами Рис.33 При этом координатные оси исходной системы Оху поворачиваются на угол ^ (рис.33). Заменим переменные х и у в формуле (I) их выражениями (2) через и вычислим коэффициент 2b при произведении Он равен и обращается в нуль, если Так как полученное уравнение разрешимо относительно , то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.
Приступая ко второму этапу преобразования, будем считать, что исходный многочлен /(я, у) уже имеет вид где а2 + с2 >0.
Для определенности положим с Ф 0 (это не ограничивает общности наших рассуждений, так как заменой я и у в случае необходимости этого всегда можно добиться). 2-й шаг. Переносом начала координат можно достичьдальнейшего упрощения вида м ногочле-на f(x, у). Эта операция описывается следующими формулами: координатные оси новой системы получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, -р) (рис.34). Укажем конкретные значения а и р. Возможны три случая Тогда, полагая Рис. 34 О) е получаем глс .
Домножснием обеих частей уравнения из п. I на -1 и заменой X на У, а У на в случае необходимости) всегда можно добиться того, чтобы Полагая получим гиперболу Полагая получим — пару пересекающихся прямых: Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса. Название можно объяснить некоторым сходством этого уравнения с уравнением лары пересекающихся прямых.
Всегда можно добиться того, чтобы В D (заменив, в случае необходимости, X на -X). Полагая получим параболу . Можно считать, что В 0. 1. Е Полагая получим — пару параллельных прямых. 2. Е > 0. Полагая получим На действительной плоскости нет ни одной точки, координаты которой обращали бы это уравнение (пары мнимых пара>1лелыыхпрямых) в тождество. 3. Е = 0. Тогда — пара совпадающих прямых. Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.
Оптическое свойство кривых второго
порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка уравнение линии второго порядка. Введем следующие обозначения Числа D и Д не зависят от выбора системы координат на плоскости и называются инвариантами.
Из приводимой таблицы видно, какому сочетанию знаков определителей D и Д соответствует та или иная линия второго порядка. Задача. Убедитесь в том, что d и Д при рассмотренных преобразованиях системы координат действительно остаются неизменными. ^ Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных Эллипс Мнимый эллипс Пара мнимых пересекающихся прямых Гипербола Пара пересекающихся прямых Парабола Пара параллельных прямых Пара мнимых параллельных прямых Парасовпадаюших прямых
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://reshimvse.com/zadacha.php?id=36959
http://natalibrilenova.ru/opticheskoe-svojstvo-krivyih-vtorogo-poryadka-kasatelnyie-k-ellipsu-i-giperbole/
Фокусное свойство гиперболы
Отрезок,
соединяющий фокус с точкой на гиперболе
называется фокальным
радиусом .
Утверждение. Пусть 
радиус с левого фокуса 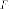
а 
радиус с правого фокуса 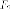
одной и той же точки 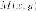
на гиперболе.
Тогда
для точек левой ветви
гиперболы
а
для точек правой ветви
Доказательство. Пусть — расстояние от
точки на
гиперболе к левому фокуса. Вычислим
ее:
Аналогично
находим
Рассмотрим правую ветвь. Для
точек правой ветви имеем 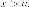
как 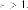
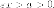
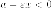
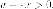
модули, находим
Рассмотрим левую ветвь. Для
точек левой ветви имеем 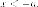
как 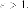

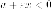
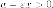
модули, находим
Как
следствие получаем фокусное
свойство гиперболы.
Для
любой точки на гиперболе
Доведння. Если
точка находится на правой ветке,
то 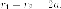
же точка на левой ветке,
тогда 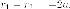
Фокусное
свойство полностью Характеризуя
гиперболу.
Упражнение. Доказать,
что геометрическое место точек, разность
расстояний от которых до двух
различных заданных
точек 
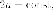
гиперболой с фокусами 
действительной полуосью
Директориальна свойство гиперболы
Утверждение. Для
биде точку 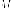
гиперболе
где — расстояния
от точки до
соответствующих директрис.
Доказательство. Рассмотрим
правую ветвь, тогда
Итак,
Для
левой ветви доведите самостоятельно.
Директориальна
свойство полностью Характеризуя
гиперболу.
Упражнение. Пусть — фиксированная
прямая, — фиксированная
точка, не лежит на этой
прямой. 

место точек 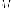
плоскости, отношение расстояний от
которых до 
расстояний от 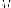

величина постоянная 
гиперболой с
эксцентриситетом 

директрисой
Уравнение касательной к гиперболе.
Утверждение. Если
точка 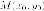
гиперболе, то уравнение касательной к
гиперболе в этой точке имеет вид:
Доказательство аналогичное
доказательству для касательной к
эллипсу, проведите его самостоятельно.
Упражнение. Докажите,
что фокусы гиперболы расположены по
разные стороны от касательной в любой
точке гиперболы.
Пример. С
точки 
касаются гиперболы
Точка 
принадлежит гиперболе. Записываем
уравнение касательной к гиперболе в
неизвестной точке 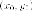
принадлежащей гиперболе:
Эта
касательная должна проходить через
точку 
Поскольку
точка 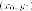
гиперболе, то 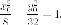
Есть
два корня этого уравнения 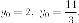
имеем две точки
соприкосновения 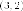
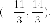
искомых касательных

Оптическая свойство гиперболы.
Утверждение. Касательная
к гиперболы образует равные углы с
локальными радиусами.
Доказательство. Пусть — касающаяся
гиперболы в
точке ее
уравнение
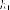
касательной от левого
фокуса 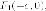
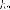
касательной от правого
фокуса 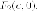
где — модуль
вектора нормали касательной. Очевидно,
что и
так как оба угла острые, то с равенства
синусов следует равенство самых
углов.
Если
представить гиперболу как зеркальную
кривую, то по законам оптики луч света,
выпущенный с одной фокуса, после отражения
от гиперболы идет так, будто его выпустили
из второго фокуса.
Другие
виды уравнений второго порядка.
Множество
точек 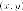
плоскости, удовлетворяющих
уравнению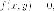
второго порядка от двух переменных,
называется кривой второго порядка.
Эллипс,
гипербола и парабола не
исчерпывают весь класс кривых второго
порядка. Рассмотрим другие виды уравнений
и соответствующих кривых.
Воображаемый
эллипс.
Эта
«кривая» задает пустую множество точек
на плоскости, но это множество задается
многочленом 2-го порядка. Эта «кривая»
имеет две «оси симметрии» и один
«центр симметрии».
Пара
прямых, которые пересекаются.
Действительно,
разложение левой части на множители
приводит к паре прямых
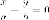
которые
пересекаются в точке 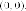
один центр симметрии.
Пара
мнимых прямых, которые пересекаются.
Единственной
точкой на плоскости, удовлетворяет
этому уравнению является точка 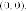
говорят о паре мнимых прямых, пересекающихся
в действительной точке. Эта «кривая»
имеет две «оси симметрии» и «центр
симметрии».
Пара
параллельных прямых.
Это
уравнение задает пару прямых

которые
очевидно параллельны. Эта «кривая»
имеет бесконечно много осей симметрии
(перпендикулярных этим прямым) и линию
центров симметрии – ось
Пара
параллельных воображаемых прямых.
Это
уравнение задает пустую множество точек
на плоскости, но по аналогии с предыдущим
случаем эту «кривую» называют парой
параллельных воображаемых прямых. Эта
«кривая» имеет бесконечно много «осей
симметрии» и «линию центров
симметрии», — ось
Пара
прямых, совпадают.
Это
уравнение задает одну прямую — ось 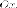
так как эта прямая является предельной
для пары прямых

говорят о паре прямых, совпадают. Эта
кривая так же имеет бесконечно много
осей симметрии, перпендикулярных
оси
линию центров симметрии- ось
Классификационная
теорема для кривых второго порядка.
Сущность
классификационной теоремы состоит в
том, что выбором прямоугольной декартовой
системы координат уравнения любой
кривой 2-го порядка может быть приведено
к уравнению эллипса, гиперболы, параболы,
воображаемого эллипса и перечисленным
5 типам уравнений пар прямых.
Эллипс
(действительный и мнимый), гипербола
и парабола образуют
класс кривых 2-го порядка, которые
не распадаются. Остальные
кривых 2-го порядка — это
кривые, которые
распадаются (по
парам прямых).
По
количеству центров симметрии кривые
2-го порядка делят на центральные,
имеющих единый центр симметрии,
и нецентральные,
не имеющих центра симметрии или имеющих
более одного центра симметрии. К типу
центральных относятся эллипсы
(действительный и мнимый), гипербола,
пары прямых, пересекающихся (действительных
и мнимых). К нецентральных
относятся парабола,
пары параллельных прямых (действительных
и мнимых) и пара прямых, совпадают.
Заметим,
что в пересечении этих классов
лежит парабола,
она является единственной нецентральной
кривой 2-го порядка, не
распадается.
Теорема . Пусть
уравнение
кривой второго порядка. Тогда
существует декартова прямоугольная
система координат, в которой уравнение
данной кривой приводится к одному
из 
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #