Как найти уравнение касательной линии - Исправление недочетов и поиск решений вместе с Examum.ru

Download Article

Unlike a straight line, a curve’s slope constantly changes as you move along the graph. Calculus introduces students to the idea that each point on this graph could be described with a slope, or an «instantaneous rate of change.» The tangent line is a straight line with that slope, passing through that exact point on the graph. To find the equation for the tangent, you’ll need to know how to take the derivative of the original equation.

1
Sketch the function and tangent line (recommended). A graph makes it easier to follow the problem and check whether the answer makes sense. Sketch the function on a piece of graph paper, using a graphing calculator as a reference if necessary. Sketch the tangent line going through the given point. (Remember, the tangent line runs through that point and has the same slope as the graph at that point.)
- Example 1: Sketch the graph of the parabola $f(x)=0.5x^{2}+3x-1$ . Draw the tangent going through point (-6, -1).
  You don’t know the tangent’s equation yet, but you can already tell that its slope is negative, and that its y-intercept is negative (well below the parabola vertex with y value -5.5). If your final answer doesn’t match these details, you’ll know to check your work for mistakes.
2

Take the first derivative to find the equation for the slope of the tangent line.^[1] For function f(x), the first derivative f'(x) represents the equation for the slope of the tangent line at any point on f(x). There are many ways to take derivatives. Here’s a simple example using the power rule:^[2]

Advertisement
3
Enter the x value of the point you’re investigating.^[3] Read the problem to discover the coordinates of the point for which you’re finding the tangent line. Enter the x-coordinate of this point into f'(x). The output is the slope of the tangent line at this point.
- Example 1 (cont.): The point mentioned in the problem is (-6, -1). Use the x-coordinate -6 as the input for f'(x):
  f'(-6) = -6 + 3 = -3
  The slope of the tangent line is -3.
4

Write the tangent line equation in point-slope form. The point-slope form of a linear equation is $y-y_{1}=m(x-x_{1})$ , where m is the slope and $(x_{1},y_{1})$ is a point on the line.^[4] You now have all the information you need to write the tangent line’s equation in this form.
5
Confirm the equation on your graph. If you have a graphing calculator, graph the original function and the tangent line to check that you have the correct answer. If working on paper, refer to your earlier graph to make sure there are no glaring mistakes in your answer.
- Example 1 (cont.): The initial sketch showed that the slope of the tangent line was negative, and the y-intercept was well below -5.5. The tangent line equation we found is y = -3x — 19 in slope-intercept form, meaning -3 is the slope and -19 is the y-intercept. Both of these attributes match the initial predictions.
6

Try a more difficult problem. Here’s a run-through of the whole process again. This time, the goal is to find the line tangent to $f(x)=x^{3}+2x^{2}+5x+1$ at x = 2:

1
Find the extreme points on a graph. These are points where the graph reaches a local maximum (a point higher than the points on either side), or local minimum (lower than the points on either side). The tangent line always has a slope of 0 at these points (a horizontal line), but a zero slope alone does not guarantee an extreme point. Here’s how to find them:^[5]
- Take the first derivative of the function to get f'(x), the equation for the tangent’s slope.
- Solve for f'(x) = 0 to find possible extreme points.
- Take the second derivative to get f»(x), the equation that tells you how quickly the tangent’s slope is changing.
- For each possible extreme point, plug the x-coordinate a into f»(x). If f»(a) is positive, there is a local minimum at a. If f»(a) is negative, there is a local maximum. If f»(a) is 0, there is an inflection point, not an extreme point.
- If there is a maximum or minimum at a, find f(a) to get the y-coordinate.
2
Find the equation of the normal. The «normal» to a curve at a particular point passes through that point, but has a slope perpendicular to a tangent. To find the equation for the normal, take advantage of the fact that (slope of tangent)(slope of normal) = -1, when they both pass through the same point on the graph.^[6] In other words:
- Find f'(x), the slope of the tangent line.
- If the point is at x = a, find f'(a) to find the slope of the tangent at that point.
- Calculate ${frac {-1}{f'(a)}}$ to find the slope of the normal.
- Write the normal equation in slope-point form.

Add New Question

Question

How do you calculate the slope of a tangent line?

Jake Adams

Academic Tutor & Test Prep Specialist

Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.

Academic Tutor & Test Prep Specialist

Expert Answer
Question

How do I find the equations of 2 lines that are tangent to a graph given the slope?

The equation for a line is, in general, y=mx+c. To find the equations for lines, you need to find m and c. m is the slope. For example, if your line goes up two units in the y direction, for every three units across in the x direction, then m=2/3. If you have the slope, m, then all you need now is c. To find c in any line, you can use any (x,y) points you know. In the case of a line that is tangent to a graph, you can use the point (x,y) where the line touches the graph. If you use that x and that y and the slope m, you can use algebra to find c. y=mx+c, so, c=y-mx. Once you have c, you have the equation of the line! Done.
Question

How do I find the equation of the line that is tangent to the graph of f(x) and parallel to the line y = 2x + 3?

Parallel lines always have the same slope, so since y = 2x + 3 has a slope of 2 (since it’s in slope-intercept form), the tangent also has a slope of 2. Now you also know that f'(x) will equal 2 at the point the tangent line passes through. Differentiate to get the equation for f'(x), then set it equal to 2. Now you can solve for x to find your x-coordinate, plug that into f(x) to find the y-coordinate, and use all the information you’ve found to write the tangent line equation in point-slope form.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

If necessary, start by rewriting the initial equation in standard form: f(x) = … or y = …

Video

About This Article

Article SummaryX

To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope. Enter the x value of the point you’re investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. For examples of tangent line equations, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,185,129 times.

Did this article help you?

Источник

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin{gather*} (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end{gather*}

Уравнение касательной к кривой (y=f(x)) в точке (x_0) имеет вид: $$ y=f'(x_0)(x-x_0)+f(x_0) $$ при условии, что производная (f'(x_0)=aneinfty) — существует и конечна.

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace{f'(x_0)}_{=k}x+underbrace{f(x_0)-f'(x_0)cdot x_0}_{=b} $$

Уравнение касательной с угловым коэффициентом: begin{gather*} y=kx+b\ k=f'(x_0), b=f(x_0)-f'(x_0)cdot x_0 end{gather*}

п.2. Алгоритм построения касательной

На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)

Например:

Пусть (f(x)=x^2+3).
Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

В случае, если производная (f'(x_0)=pminfty) — существует, но бесконечна, в точке (x_0) проходит вертикальная касательная (x=x_0).

Внимание!

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]{x}).

Например:

Пусть (f(x)=sqrt[5]{x-1}+1).
Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]{1-1}+1=1)
(f'(x)=frac15(x-1)^{frac15-1}+0=frac15(x-1)^{-frac45}=frac{1}{5(x-1)^{frac45}} )
(f'(x_0)=frac{1}{5(1-1)^{frac45}}=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin{array}{l} x=0\ x=-2 end{array} right. $$ Две точки на оси: (0;0) и (-2;0).
Касательная в точке (x_0=0): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end{gather*} Касательная в точке (x_0=-2): begin{gather*} f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end{gather*}

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: (f'(x)=4x+4)
По условию (f'(x_0)=tgalpha=tg45^circ=1)
Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin{gather*} f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac{15}{8} end{gather*} Уравнение касательной: begin{gather*} y=1cdotleft(x+frac34right)-frac{15}{8}=x-frac98 end{gather*}

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2).
Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin{gather*} f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end{gather*} Точка касания (x_0=-frac32) begin{gather*} f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end{gather*} Уравнение касательной: begin{gather*} y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end{gather*} Или, в каноническом виде: begin{gather*} 2x+y+frac92=0 end{gather*}

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0).
Получаем уравнение: (f'(x_0)=0). begin{gather*} 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end{gather*} Точка касания (x_0=-1) begin{gather*} f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end{gather*} Уравнение касательной: begin{gather*} y=0cdot(x+1)-2=-2 end{gather*}

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 2. Напишите уравнение касательной к графику функции в заданной точке:
a) ( f(x)=frac5x+frac x5, x_0=4 ) begin{gather*} f(x_0)=frac54+frac45=frac{25+16}{20}=frac{41}{20}\ f'(x)=left(frac5xright)’+left(frac x5right)’=-frac{5}{x^2}+frac15=frac{-25+x^2}{5x^2}=frac{x^2-25}{5x^2}\ f'(x_0)=frac{4^2-25}{5cdot 4^2}=-frac{9}{80} end{gather*} Уравнение касательной: $$ y=-frac{9}{80}(x-4)+frac{41}{20}=-frac{9}{80}x+frac{9}{20}+frac{41}{20}=-frac{9}{80}x+2,5 $$
б) ( f(x)=frac{x^2+5}{3-x}, x_0=2 ) begin{gather*} f(x_0)=frac{2^2+5}{3-2}=frac91=9\ f'(x)=frac{(x^2+5)'(3-x)-(x^2+5)(3-x)’}{(3-x)^2}=frac{2x(3-x)+(x^2+5)}{(3-x)^2}=\ =frac{6x-2x^2+x^2+5}{(3-x)^2}=frac{-x^2+6x+5}{(3-x)^2}\ f'(x_0)=frac{-2^2+6cdot 2+5}{(3-2)^2}=13 end{gather*} Уравнение касательной: $$ y=13(x-2)+9=13x-26+9=13x-17 $$

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac{x^2+2}{x+3}-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac{1}{k_1}=-frac{1}{11}) begin{gather*} f'(x)=left(frac{x^2+2}{x+3}right)’-x’=frac{2x(x+3)-(x^2+2)cdot 1}{(x+3)^2}-1=frac{2x^2+6x-x^2-2-(x+3)^2}{(x+3)^2}=\ =frac{x^2+6x-2-x^2-6x-9}{(x+3)^2}=- frac{11}{(x+3)^2} end{gather*} В точке касания: begin{gather*} f'(x_0)=k_2Rightarrow=-frac{11}{(x+3)^2}=-frac{1}{11}Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin{array}{l} x=-14\ x=8 end{array} right. end{gather*}
Уравнение касательной при (x_0=-14) begin{gather*} f(x_0)=frac{(-14)^2+2}{-14+3}+14=frac{198}{-11}+14=-18+14=-4\ y=-frac{1}{11}(x+14)-4=-frac{x+58}{11} end{gather*} Уравнение касательной при (x_0=8) begin{gather*} f(x_0)=frac{8^2+2}{8+3}-8=frac{66}{11}-8=-2\ y=-frac{1}{11}(x-8)-2=-frac{x+14}{11} end{gather*}
Ответ: точка касания (-14;-4), уравнение (y=-frac{x+58}{11})
и точка касания (8;-2), уравнение (-frac{x+14}{11})

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin{gather*} f_1′(x)=2x-5, f_2′(x)=2x+1 end{gather*} Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin{gather*} g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end{gather*} Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin{gather*} begin{cases} 2a-5=2b+1\ 6-a^2=1-b^2 end{cases} Rightarrow begin{cases} 2(a-b)=6\ a^2-b^2=5 end{cases} Rightarrow begin{cases} a-b=3\ (a-b)(a+b)=5 end{cases} Rightarrow begin{cases} a-b=3\ a+b=frac53 end{cases} Rightarrow \ Rightarrow begin{cases} 2a=3+frac53\ 2b=frac53-3 end{cases} Rightarrow begin{cases} a=frac73\ b=-frac23 end{cases} end{gather*} Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac{49}{9}=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin{gather*} a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac{49}{9}-frac{35}{3}+6=frac{49-105+54}{9}=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac{4-6+9}{9}=frac79 end{gather*}
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.

Решим уравнение: (x^4+3x^2+2x=2x-1) begin{gather*} x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac{-3pmsqrt{5}}{2} end{gather*} Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin{gather*} 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin{array}{l} x=0\ 2x^2+3=0 end{array} right. Rightarrow left[ begin{array}{l} x=0\ x^2=-frac32 end{array} right. Rightarrow left[ begin{array}{l} x=0\ xinvarnothing end{array} right. Rightarrow x=0 end{gather*} Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Ищем расстояние между двумя параллельными прямыми:
(y=2x) и (y=2x-1).
Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0).

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin{gather*} 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac{0,4}{2}=-0,2 end{gather*} Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt{0,4^2+(-0,2)^2}=0,2sqrt{2^2+1^2}=frac{sqrt{5}}{5})
Ответ: (frac{sqrt{5}}{5})

Источник

Уравнение касательной к графику функции

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace_<=k>x+underbrace_ <=b>$$

п.2. Алгоритм построения касательной

Пусть (f(x)=x^2+3).
Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]).

Пусть (f(x)=sqrt[5]+1).
Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]<1-1>+1=1)
(f'(x)=frac15(x-1)^<frac15-1>+0=frac15(x-1)^<-frac45>=frac<1><5(x-1)^<frac45>> )
(f'(x_0)=frac<1><5(1-1)^<frac45>>=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin x=0\ x=-2 end right. $$ Две точки на оси: (0;0) и (-2;0).
Касательная в точке (x_0=0): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end Касательная в точке (x_0=-2): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end

Общее уравнение касательной: (f'(x)=4x+4)
По условию (f'(x_0)=tgalpha=tg45^circ=1)
Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac<15> <8>end Уравнение касательной: begin y=1cdotleft(x+frac34right)-frac<15><8>=x-frac98 end

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2).
Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end Точка касания (x_0=-frac32) begin f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end Уравнение касательной: begin y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end Или, в каноническом виде: begin 2x+y+frac92=0 end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0).
Получаем уравнение: (f'(x_0)=0). begin 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end Точка касания (x_0=-1) begin f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end Уравнение касательной: begin y=0cdot(x+1)-2=-2 end

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac<1>=-frac<1><11>) begin f'(x)=left(fracright)’-x’=frac<2x(x+3)-(x^2+2)cdot 1><(x+3)^2>-1=frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\ =frac<(x+3)^2>=- frac<11> <(x+3)^2>end В точке касания: begin f'(x_0)=k_2Rightarrow=-frac<11><(x+3)^2>=-frac<1><11>Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin x=-14\ x=8 end right. end
Уравнение касательной при (x_0=-14) begin f(x_0)=frac<(-14)^2+2><-14+3>+14=frac<198><-11>+14=-18+14=-4\ y=-frac<1><11>(x+14)-4=-frac <11>end Уравнение касательной при (x_0=8) begin f(x_0)=frac<8^2+2><8+3>-8=frac<66><11>-8=-2\ y=-frac<1><11>(x-8)-2=-frac <11>end
Ответ: точка касания (-14;-4), уравнение (y=-frac<11>)
и точка касания (8;-2), уравнение (-frac<11>)

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin f_1′(x)=2x-5, f_2′(x)=2x+1 end Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin begin 2a-5=2b+1\ 6-a^2=1-b^2 end Rightarrow begin 2(a-b)=6\ a^2-b^2=5 end Rightarrow begin a-b=3\ (a-b)(a+b)=5 end Rightarrow begin a-b=3\ a+b=frac53 end Rightarrow \ Rightarrow begin 2a=3+frac53\ 2b=frac53-3 end Rightarrow begin a=frac73\ b=-frac23 end end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac<49><9>=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac<49><9>-frac<35><3>+6=frac<49-105+54><9>=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac<4-6+9><9>=frac79 end
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Решим уравнение: (x^4+3x^2+2x=2x-1) begin x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac<-3pmsqrt<5>> <2>end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin x=0\ 2x^2+3=0 end right. Rightarrow left[ begin x=0\ x^2=-frac32 end right. Rightarrow left[ begin x=0\ xinvarnothing end right. Rightarrow x=0 end Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac<0,4><2>=-0,2 end Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt<0,4^2+(-0,2)^2>=0,2sqrt<2^2+1^2>=frac<sqrt<5>><5>)
Ответ: (frac<sqrt<5>><5>)

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .

Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .

Необходимо найти производную в точке со значением — 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5

Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где

Касательная не существует;
Касательная располагается параллельно о х ;
Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что

y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )

Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3

Вычисляем значение функции в точке х = — 2 , где получаем, что

y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .

— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3

Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3

Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk

3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z — множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3

y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид

y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3

Ответ: уравнение касательной можно представить как

y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4

Имеем, что точки касания — 23 4 ; — 5 + 3 4 .

Ответ: уравнение касательной принимает вид

Уравнение касательной к графику функции

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

В чем заключается геометрический смысл производной

Одну из главных ролей в записи касательной к графику играет производная, поэтому определим ее геометрический смысл.

Пусть задана произвольная функция y = f(x).

На графике этой функции возьмем точку А с координатами . А теперь выберем точку B с координатами недалеко от точки А.

Проведем через точки A и B прямую.

Угол наклона прямой к оси абсцисс обозначим буквой .

Проведем через точку А прямую, параллельную оси абсцисс, а через точку B — прямую, параллельную оси ординат. Пусть эти две прямые пересекутся в точке C.

Тогда катет , а катет .

Если взять отношения этих значений , то получим отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике ABC, что равно .

Если уменьшать расстояние между точками A и B, то будут уменьшаться длины отрезков и и в какой-то момент точка В совпадет с точкой A, а отношение станет равно производной функции y = f(x) в точке .

Тут может возникнуть вопрос: при чем здесь геометрический смысл производной, если мы начали с касательной?

Касательная — это прямая. Вспомним уравнение прямой: y = kx + b, где k — это коэффициент наклона прямой, и он равен тангенсу угла между прямой и осью абсцисс. А теперь совмещаем все данные и делаем вывод, что .

Это очень важный для нас вывод, попробуем применить его на практике, а именно на задачах формата профильного ЕГЭ по математике.

Решение задач

Задача 1

К графику функции y = f(x) проведена касательная в точке с абсциссой . Нужно найти угловой коэффициент касательной к графику данной функции.

Из теории выше мы узнали, как найти угловой коэффициент касательной — он равен тангенсу угла наклона касательной к графику функции в точке. Значит, через целочисленные точки на прямой построим прямоугольный треугольник и найдем отношение противолежащего катета к прилежащему — получится .

Ответ: 3.

Задача 2

К графику функции y = f(x) проведена касательная в точке с абсциссой . Определите угловой коэффициент касательной в точке .

Действуйте по уже известным правилам. Получился ответ 0,25? А вот и нет! В данном случае нужно обратить внимание на убывание графика касательной. Видите, она слева направо идет вниз? Значит, к ответу нужно добавить минус и записать его — получится −0,25.

Ответ: −0,25.

Задача 3

На рисунке изображен график функции y = f(x), определенной на интервале (−8; 3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 36.

Надеюсь, вы не подумали, что мы будем изображать прямую y = 36 и искать касательные, параллельные ей. 🤯 Достаточно будет рассуждений. Прямая y = 36 — горизонтальная прямая с k = 0, а значит, и у касательных к графику k = 0 или тангенс угла наклона касательной к графику функции также будет равен нулю, что может быть только в точках экстремума функции или, проще говоря, в «бугорках» функции.

В ответе просили указать количество таких точек, значит, ответ — 5.

Ответ: 5.

Задача 4

Прямая y = 4x + 13 параллельна касательной к графику функции . Найдите абсциссу точки касания.

Если прямая параллельна касательной к графику функции, то у них будут равные угловые коэффициенты. Угловой коэффициент прямой y = 4x + 13 равен 4, а угловой коэффициент касательной к графику функции равен производной от этой функции, то есть 2x − 3. Приравняем полученные значения и найдем x:

Ответ: 3,5 — абсцисса точки касания.

Как составить уравнение касательной к графику функции

Но как поступать, если нужно составить уравнение касательной к графику функции?

Уравнение касательной к графику функции y = f(x) в точке находится по формуле .

Для упрощения понимания этой формулы запишем алгоритм составления уравнения касательной к кривой y = f(x) в точке :

Вычислим значение функции в точке касания, для этого подставим в y = f(x) и посчитаем.

Продифференцируем функцию y = f(x).

Вычислим значение функции в точке касания, для этого подставим в и посчитаем.

Составим уравнение касательной и приведем его к виду y = kx + b.

Задача 5

Запишите уравнение касательной к параболе в точке .

Воспользуемся алгоритмом выше:

Вычислим значение функции в точке касания, для этого подставим в и посчитаем: .

Вычислим значение функции в точке касания: .

Все найденные значения подставим в уравнение касательной: .

Приведем полученное выражение к виду y = kx + b: y = −2x + 24.

Ответ: уравнение касательной y = −2x + 24.

По условию задачи нас не просили, но мы можем изобразить график квадратичной функции и касательную к параболе для проверки. Если получилась лишь одна точка касания с правильными координатами, значит, наши расчеты были верны!

Некоторые темы математики, как клубок ниток, содержат в себе понятия и правила из других тем. Не понимая прошлые темы, не удастся разобраться и в новой. На каждом уроке курсов обучения математике в онлайн-школе Skysmart мы актуализируем уже имеющиеся знания, поэтому не разобраться не получится. Приходите на бесплатный вводный урок за подробным разбором сильных и слабых сторон и конкретными рекомендациями, как улучшить оценки и подготовиться к экзаменам!

Уравнение касательной к графику функции

Онлайн калькулятор для вычисления уравнения касательной к графику функции.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0
задано, то переходим к п.2.
Нахождение производной y'(x).
Вычисление значения производной при x0.
Запись уравнения касательной к кривой линии в форме: yk = y0 + y'(y0)(x — x0)

Калькулятор поможет составить и решить уравнение касательной к графику функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.

источники:

http://zaochnik.com/spravochnik/matematika/proizvodnye/kasatelnaja-k-grafiku-funktsii-v-tochke/

http://skysmart.ru/articles/mathematic/uravnenie-kasatelnoj-k-grafiku-funkcii

http://allcalc.ru/node/689

Источник

В этой статье мы разберем все типы задач на нахождение уравнения касательной.

Вспомним геометрический смысл производной: если к графику функции y=f(x) в точке x_0 проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке x_0 .

$k=tg{alpha}=f^{prime}(x_0)$

Возьмем на касательной произвольную точку с координатами ( x;y) :

И рассмотрим прямоугольный треугольник 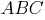ABC :

В этом треугольнике $tg{alpha}={BC}/{AB}={y-f(x_0)}/{x-x_0}=f{prime}(x_0)$

Отсюда ${y-f(x_0)}= f{prime}(x_0)(x-x_0)$

Или

$y=f(x_0)+ f{prime}(x_0)(x-x_0)$

Это и есть уравнение касательной, проведенной к графику функции y=f(x) в точке x_0 .

Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти f(x_0) и $f{prime}(x_0)$ .

Есть три основных типа задач на составление уравнения касательной.

1. Дана точка касания x_0

2. Дан коэффициент наклона касательной, то есть значение производной функции y=f(x) в точке x_0 .

3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.

Рассмотрим каждый тип задач.

1. Написать уравнение касательной к графику функции в точке x_0=1 .

а) Найдем значение функции в точке x_0=1 .

б) Найдем значение производной в точке x_0=1 . Сначала найдем производную функции y=f(x)

$f{prime}(x)=3x^2-4x$

$f{prime}(1)=3*1^2-4*1=-1$

Подставим найденные значения в уравнение касательной:

Раскроем скобки в правой части уравнения. Получим: y=-x+3

Ответ: y=-x+3 .

2. Найти абсциссы точек, в которых касательные к графику функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ параллельны оси абсцисс.

Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ в точках касания равно нулю.

а) Найдем производную функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ .

$y{prime}=x^3-8x^2+15x$

б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :

Приравняем каждый множитель к нулю, получим:

Ответ: 0;3;5

3. Написать уравнения касательных к графику функции , параллельных прямой y=-x+3 .

Касательная параллельна прямой y=-x+3 . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.

Это второй тип задач на нахождение уравнения касательной.

Итак, у нас дана функция и значение производной в точке касания.

а) Найдем точки, в которых производная функции равна -1.

Сначала найдем уравнение производной.

Нам нужно найти производную дроби.

$({u/v})^{prime}={u{prime}v-v{prime}u}/{v^2}$

$y{prime}={(3x-4){prime}(2x-3)-(2x-3){prime}(3x-4)}/{(2x-3)^2}={3(2x-3)-2(3x-4)}/{(2x-3)^2}={-1}/{(2x-3)^2}$

Приравняем производную к числу -1.

${-1}/{(2x-3)^2}=-1$

2x-3=1 или 2x-3=-1

x_0=2 или x_0=1

б) Найдем уравнение касательной к графику функции в точке x_0=2 .

Найдем значение функции в точке x_0=2 .

(по условию)

Подставим эти значения в уравнение касательной:

б) Найдем уравнение касательной к графику функции в точке x_0=1 .

Найдем значение функции в точке x_0=1 .

(по условию).

Подставим эти значения в уравнение касательной:

Ответ:

4. Написать уравнение касательной к кривой $y=sqrt{8-x^2}$ , проходящей через точку A(3,1)

Сначала проверим, не является ли точка A(3,1) точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты точки A(3,1) в уравнение функции.

$1<>sqrt{8-3^2}$ . Мы получили под корнем отрицательное число, равенство не верно, и точка A(3,1) не принадлежит графику функции и не является точкой касания.

Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания.

Найдем значение x_0 .

Пусть x_0 — точка касания. Точка A(3,1) принадлежит касательной к графику функции $y=sqrt{8-x^2}$ . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:

$1=f(x_0)+ f{prime}(x_0)(3-x_0)$ .

Значение функции $y=sqrt{8-x^2}$ в точке x_0 равно $f(x_0)= sqrt{8-{x_0}^2}$ .

Найдем значение производной функции $y=sqrt{8-x^2}$ в точке x_0 .

Сначала найдем производную функции $y=sqrt{8-x^2}$ . Это сложная функция.

$f{prime}(x)={1/{2sqrt{8-x^2}}}*(8-x^2){prime}={{-2x}/{2sqrt{8-x^2}}}$

Производная в точке x_0 равна $f{prime}(x_0)={-2{x_0}}/{2sqrt{8-{x_0}^2}}$ .

Подставим выражения для f(x_0) и $f{prime}(x_0)$ в уравнение касательной. Получим уравнение относительно x_0 :

$1=sqrt{8-{x_0}^2}+{-2{x_0}}/{2sqrt{8-{x_0}^2}}(3-x_0)$

Решим это уравнение.

Сократим числитель и знаменатель дроби на 2:

$1=sqrt{8-{x_0}^2}+{-{x_0}}/{sqrt{8-{x_0}^2}}(3-x_0)$

Приведем правую часть уравнения к общему знаменателю. Получим:

$1={8-{x_0}^2-{x_0}(3-x_0)}/{sqrt{8-{x_0}^2}}$

Упростим числитель дроби и умножим обе части на ${sqrt{8-{x_0}^2}}$ — это выражение строго больше нуля.

Получим уравнение

${8-3x_0}={sqrt{8-{x_0}^2}}$

Это иррациональное уравнение.

Решим его. Для этого возведем обе части в квадрат и перейдем к системе.

$delim{lbrace}{matrix{2}{1}{{64-48{x_0}+9{x_0}^2=8-{x_0}^2} {8-3x_0>=0} }}{ }$

Решим первое уравнение.

$10{x_0}^2-48x_0+56=0$

$5{x_0}^2-24x_0+28=0$

Решим квадратное уравнение, получим

x_0=2 или x_0=2,8

Второй корень не удовлетворяет условию , следовательно, у нас только одна точка касания и её абсцисса равна .

Напишем уравнение касательной к кривой $y=sqrt{8-x^2}$ в точке x_0=2 . Для этого подставим значение x_0=2 в уравнение $y=sqrt{8-{x_0}^2}+{-2{x_0}}/{2sqrt{8-{x_0}^2}}(x-x_0)$ — мы его уже записывали.

Получим:

$y=sqrt{8-{2}^2}-{2*{2}}/{2sqrt{8-{(2)}^2}}(x-2)$

Ответ: y=-x+4
И.В. Фельдман, репетитор по математике.

Источник

Геометрический смысл производной

Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!

Рассмотрим график какой-то функции ( y=fleft( x right)):

Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).

Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).

Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).

Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.

Какие значения может принимать угол ( alpha )?

Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).

Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.

Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:

grafik funktsii nahozhdenie kasatelnoj s pomoshyu proizvodnoj

По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).

Тогда отношение приращений:

( frac{Delta f}{Delta x}=frac{BC}{AC}={tg}alpha )

(так как ( angle C=90{}^circ ), то ( triangle ABC) – прямоугольный).

Давай теперь уменьшать ( Delta x).

Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).

Что же при этом станет с секущей?

Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.

Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).

Говорят, что при этом секущая занимает предельное положение.

Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная

( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),

то есть

Производная равна тангенсу угла наклона касательной к графику функции в данной точке

Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:

( y=kx+b).

За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.

Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!

То есть вот что получается:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k).

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?

Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.

Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).

С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).

Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.

Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).

Итак, сформулируем окончательно полученное правило:

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k)

nahozhdenie kasatelnoj k grafiku funktsii

Это и есть геометрический смысл производной.

Окей, все это интересно, но зачем оно нам? Вот пример:

На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).

Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).

nahozhdenie kasatelnoj k grafiku funktsii 2

Решение.

Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:

( displaystyle f’left( x right)=k= {tg}varphi).

Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.

На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Угол наклона касательной к оси ( displaystyle Ox) – это ( displaystyle angle BAC). Найдем тангенс этого угла:

( displaystyle {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2).

Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).

Ответ: ( displaystyle 1,2).

Теперь попробуй сам.

Уравнение касательной к графику функций

А сейчас сосредоточимся на произвольных касательных.

Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).

Берем линейку, пристраиваем ее к графику и чертим:

Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?

Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении

( y=kx+b).

Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:

( k={f}’left( {{x}_{0}} right)).

В нашем примере будет так:

( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)

( k={f}’left( {{x}_{0}} right)={f}’left( 2 right)=2cdot 2=4.)

Теперь остается найти ( b) . Это проще простого: ведь ( b) – значение ( y) при ( displaystyle x=0).

Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):

Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).

Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?

По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:

( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).

Соединяем все полученные формулы в уравнение прямой:

( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)

( y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right))

Это и есть уравнение касательной к графику функции ( fleft( x right)) в точке ( {{x}_{0}}).

Пример:

Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).

Решение:

На этом примере выработаем простой…

Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике

ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование

На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.

Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.

Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.

P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».

Источник