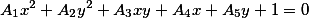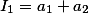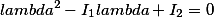Онлайн-сервис для определение вида кривой или поверхности второго порядка по инваринтам, показывается график кривой. Также находятся ортогональных инварианты и семиинваринты.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
С помощью нашего калькулятора вы научитесь строить кривые второго порядка по заданному уравнению. Чтобы вставить выражение из примера в калькулятор кликните по кнопке копирования (справа в примере), а затем нажмите кнопку «Решить».
Пример. Построить эллипс по уравнению: (x^2/2+y^2/4=1).
plot x^2/2+y^2/4=1
Пример. Построить гиперболу по уравнению: (x^2/3-y^2/4=1).
plot x^2/3-y^2/4=1
Пример. Построить параболу по уравнению: (y-x^2/3-1=0).
plot y-x^2/3-1=0
Пример. Построить кривую второго порядка по общему уравнению: (2x^2+3y^2+x*y-2x+5y-1=0). Определить вид кривой.
plot 2x^2+3y^2+x*y-2x+5y-1=0
Похожие публикации: калькулятор
Расчет кривой второго порядка на плоскости по точкам
| Элементы кривой второго порядка или координаты |
| Уравнения Ax^2+By^2+Cxy+Dx+Ey+F=0 |
| A= |
| B= |
| C= |
| D= |
| E= |
| F= |
| Полученная формула |
| Коэффициенты через пробел |
Калькулятор предназначен для расчета и создания уравнения кривых второго порядка на декартовой плоскости по нескольким точкам, от двух до пяти.
Не является секретом то, что уравнение кривой второго порядка может быть представлена формулой
Мы будем использовать чуть измененную формулу, разделив все коэффициенты на a6
отсюда видно, что кривую второго порядка можно однозначно определить по пяти точкам.
Кривая второго порядка при различных коэффициентах может превращатся в следующие «типы»:
— Эллипс
— Окружность
— Парабола
— Гипербола
— пара пересекающихся прямых
— пара паралельных несовпадающих прямых
— пары совпадающих прямых
— линии, вырождающиеся в точку
— «нулевые линии», то есть «линии», вовсе не имеющие точек
Если Вам интересны формулы при которых получаются все эти типы, то пожалуйста
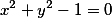
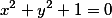
(cfrac{x^2}{a^2}+cfrac{y^2}{b^2}-1=0) — эллипс
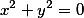
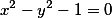
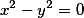
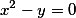
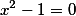
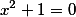
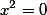
Этот сервис позволяет Вам по заданным точкам определить, какую же кривую второго порядка провести через эти точки. Кроме этого, Вы увидите все основные параметры полученной кривой второго порядка.
От Вас лишь понадобится предоставить боту от двух до пяти декартовых координат, что бы бот мог решить эту задачу.
ИНВАРИАНТЫ И СВОДНАЯ ТАБЛИЦА
Любая кривая второго порядка 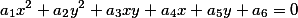
(I_2=begin{pmatrix}a_1&frac{a_3}{2}%20%20frac{a_3}{2}&%20a_2end{pmatrix})
(I_3=K_2=begin{pmatrix}a_1&%20frac{a_3}{2}%20&frac{a_4}{2}frac{a_3}{2}&%20a_2&frac{a_5}{2}frac{a_4}{2}&%20frac{a_5}{2}&a_6end{pmatrix})
https://img.abakbot.ru/cgi-bin/mathtex.cgi?I_3=K_2=begin{pmatrix}a_1&%20frac{a_3}{2}%20&frac{a_4}{2}frac{a_3}{2}&%20a_2&frac{a_5}{2}frac{a_4}{2}&%20frac{a_5}{2}&a_6end{pmatrix}
И одним семиинвариантом
если Вам интересно, откуда они появились, то рекомендуем прочитать книгу «Аналитическая геометрия — Делоне»
Характеристическое уравнение кривой второго порядка:
Таким образом сводная таблица имеет вид
| Признак типа | Признак класса | Название | Приведенное уравнение | Каноническое уравнение |
|---|---|---|---|---|
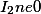 |
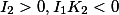 |
Эллипс | 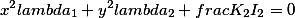 |
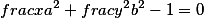 |
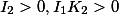 |
Мнимый эллипс | 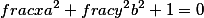 |
||
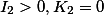 |
Точка | 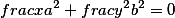 |
||
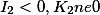 |
Гипербола | 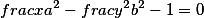 |
||
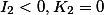 |
Пара пересекающихся прямых | 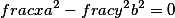 |
||
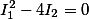 |
Окружность | 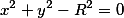 |
||
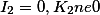 |
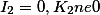 |
Парабола | 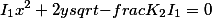 |
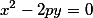 |
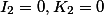 |
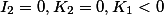 |
Пара паралельных прямых | 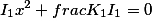 |
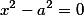 |
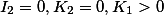 |
Пара мнимых паралельных прямых | 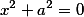 |
||
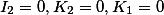 |
Пара совпадающих прямых | 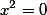 |
Анализируя написанные онлайн калькуляторы по этой теме, нашел интересную «особенность». Попробовав рассчитать по трем точкам кривую второго порядка, зная что эти точки принадлежат окружности, я с завидным постоянством получал ответ, что графиком(формой)полученного уравнения кривой является эллипс.
Нет формально, конечно стоит признать что окружность является частным примером эллипса, но ведь можно пойти дальше и признать что и эллипс и гипербола и парабола, являются лишь частным примером кривой второго порядка общего вида, и в ответах таких калькуляторов выдавать ответ пользователю «вы получили уравнение второго порядка» и всё… не соврали же…
Такое сверхлегкое трактование и смешение определений геометрических фигур, никак не способствует пониманию и сути решаемых задач. Это как в анекдоте «А теперь нарисуем квадрат со сторонами 3 на 4″(с) И не поймешь то ли рисовать квадрат, то ли прямоугольник….
Пример:
Начнем сразу с проверочного примера
Вообще, убедимся правильно ли считает бот?
Итак, есть у нас функция x*x+3x-11=y
определим значения при x=1,2,3,4,5
значения получились такие y=-7,-1,7,17,29
и зададим эти точки в качестве исходных
пишем kp2 1:-7 2:-1 3:7 4:17 5:29
в результате получаем следующее:
На первый взгляд получилось далеко не то, что должно получится.
Но если мы уберем нулевые коэффициенты, и разделим все на 0.09091 то результат будет такой
(-x^2-3*x+y+11=0)
то есть
Что и требовалось доказать в качестве правильности расчетов нашего бота.
Теперь пусть у нас есть всего лишь три точки
С координатами x=1,2,3 и y=-7,-1,7
Логично, что это тоже самое уравнение параболы что мы разбирали в первом примере. НО! при трех точках такое решение не единственное.
Давайте попробуем задать боту всего три координаты и скажем ему какого вида уравнение мы хотим получить.
Например:
Это частное уравнение кривой второго порядка в котором коэффициенты а1 и а5 равны нулю
Скажем об этом боту
kp2 0 1:-7 2:-1 3:7 0 1
где 0- показывает какие коэффициенты нам НЕ надо учитывать, а 1 — это постоянный коэффициент, то есть его находить нет необходимости. Он известен.
Видим что не учитываем 1 и 5 коэффициент.
получим
Кривая второго порядка a1*x*x+a2*y*y+a3*x*y+a4*x+a5*y+a6 = 0
Коэффициент a2 при y*y равен -0.00621100
Коэффициент a3 при x*y равен 0.03312600
Коэффициент a4 при x равен -0.46376800
Коэффициент a6 равен 1
То есть есть еще одна кривая которая проходит через заданные три точки
это
Кто желает может проверить. Но уверяю что все правильно.
|
|||||||||
|
|||||||||
|
|||||||||
|
| Уравнение | Канонический вид | Тип | Измерение |
|---|---|---|---|
| 9x^2+12xy+4y^2-24x-16y+3=0 | x^2=1 | Две параллельные прямые | Линия |
| x^2-2xy+y^2-10x-6y+25=0 | y^2=4*sqrt(2)*x | Парабола | Линия |
| 5x^2+4xy+y^2-6x-2y+2=0 | x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0 | Вырожденный эллипс | Линия |
| 5*x^2+4*x*y+8*y^2+8*x+14*y+5=0 | x^2/(3/4)^2+y^2/(1/2)^2=1 | Эллипс | Линия |
| 2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0 | z^2/(2/sqrt(2)/sqrt(3-sqrt(5)))^2+x^2/(2/sqrt(2)/sqrt(3+sqrt(5)))^2+y^2/(2/sqrt(2))^2=-1 | Мнимый эллипсоид | Поверхность |
| x^2+y^2-z^2-2*x-2*y+2*z+2=0 | x^2/1^2+y^2-z^2=-1 | Двухсторонний гиперболоид | Поверхность |
| x^2+y^2-6*x+6*y-4*z+18=0 | x^2/2+y^2-2*z=0 или x^2/2+y^2+2*z=0 | Эллиптический параболоид | Поверхность |
| x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0 | x^2/=1/14 | Две параллельные плоскости | Поверхность |