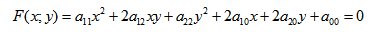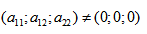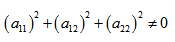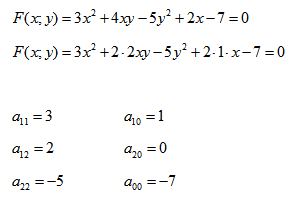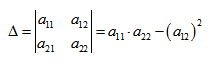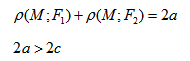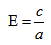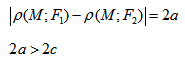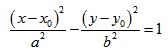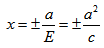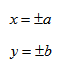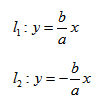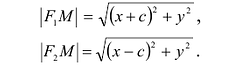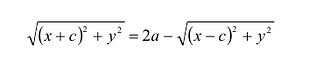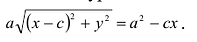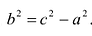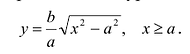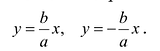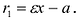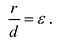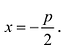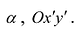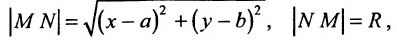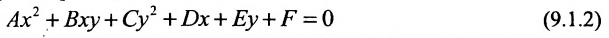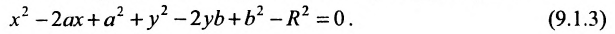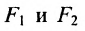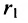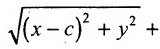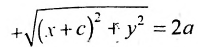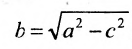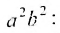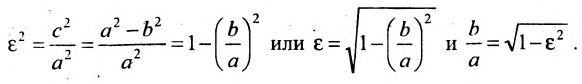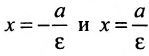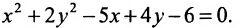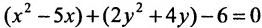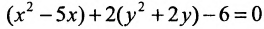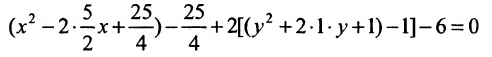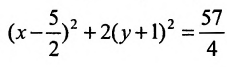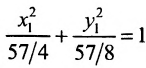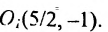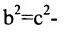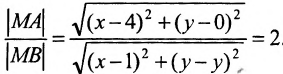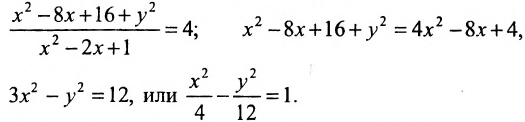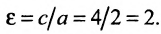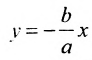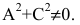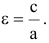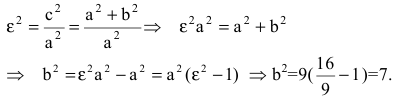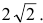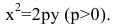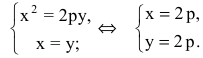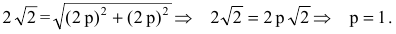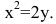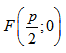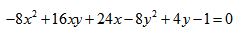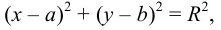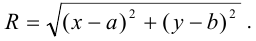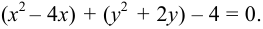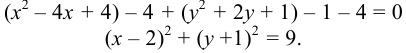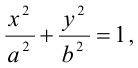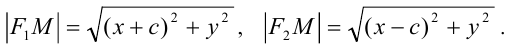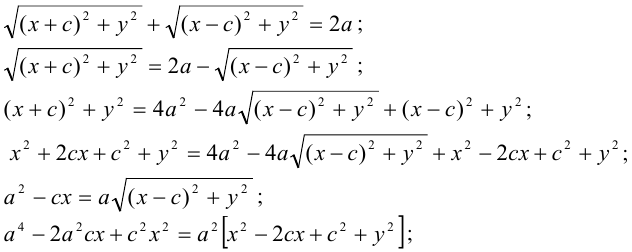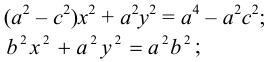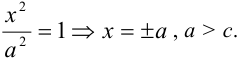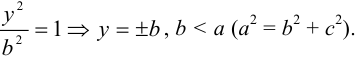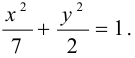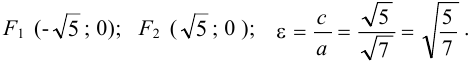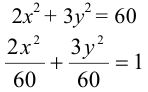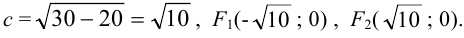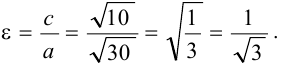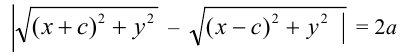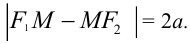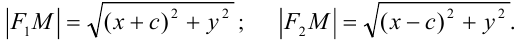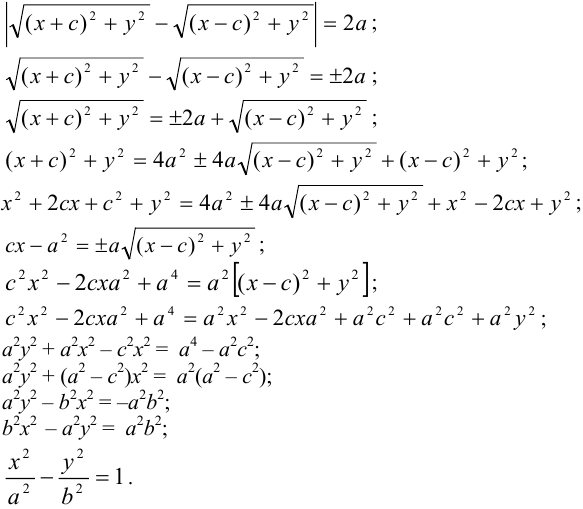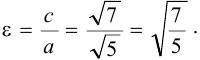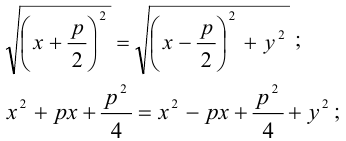Кривые второго порядка
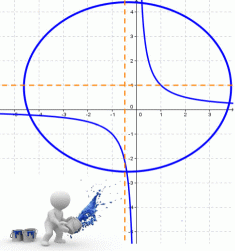
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
или можно встретить следующую форму записи:
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
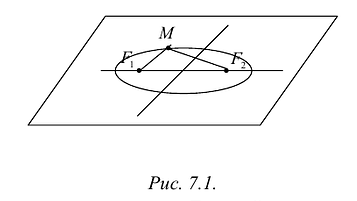
если Δ F1 и F2 — фокусы.
с — фокальное расстояние,
Каноническое уравнение эллипса с центром симметрии в начале координат:
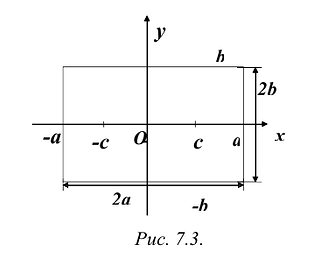
2а — большая ось эллипса, 2b — малая ось эллипса.
а — большая полуось эллипса, b — малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
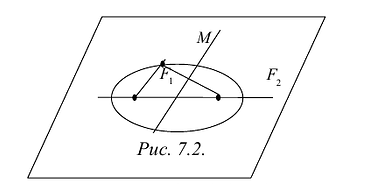
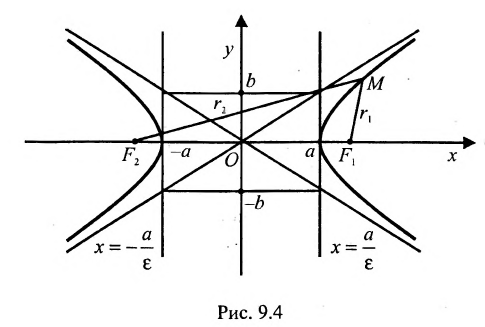
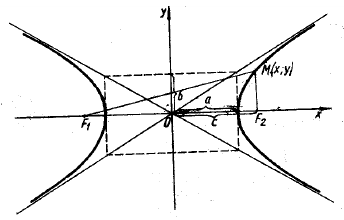
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
с — фокальное расстояние,
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:
x — действительная ось, y — мнимая ось.
а — действительная полуось, b — мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 — правая директриса, f2 — левая директриса.
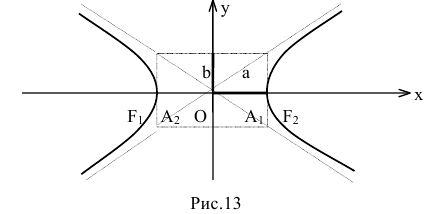
Порядок построения гиперболы :
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А 1 (-а;0), А 2 (а;0).
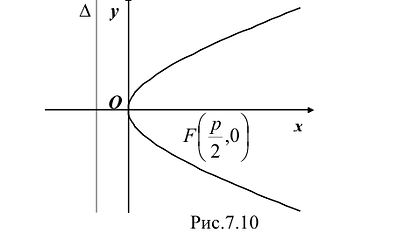
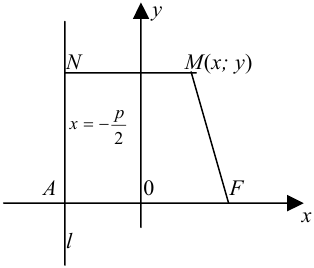
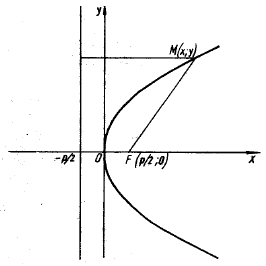
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
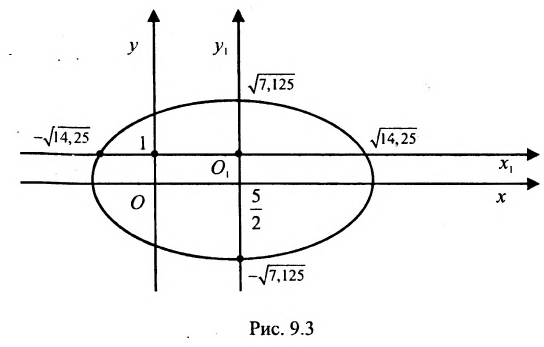
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Примеры решений: кривые второго порядка
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.
Кривые 2-го порядка: решения онлайн
Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.
Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.
Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.
Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.
Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
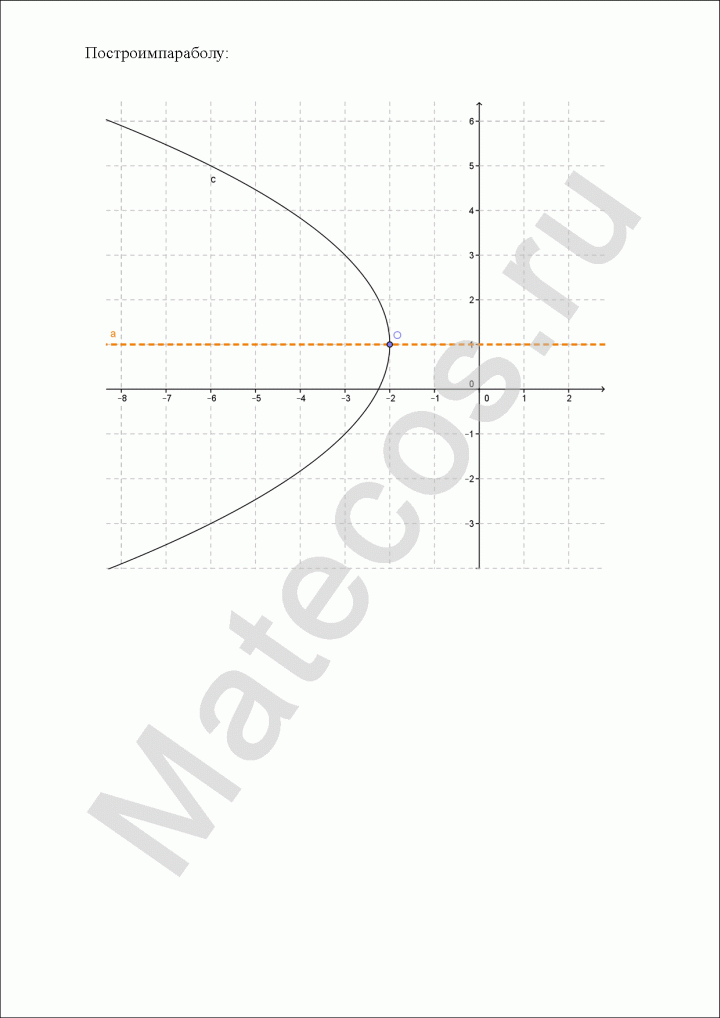
5. Постройте данную параболу.
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
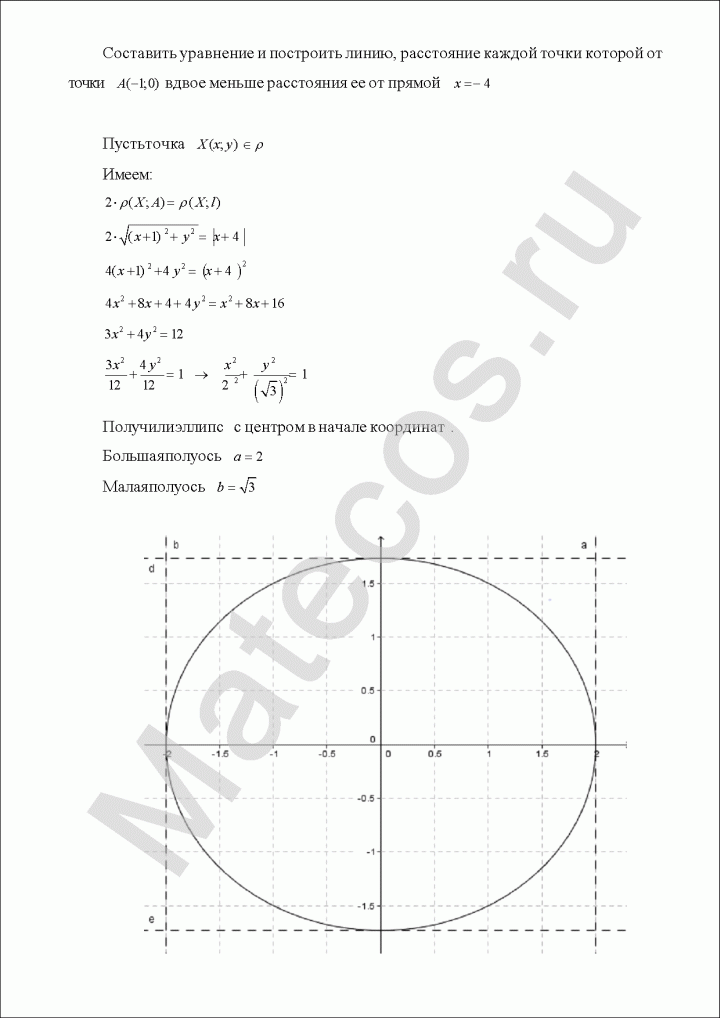
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
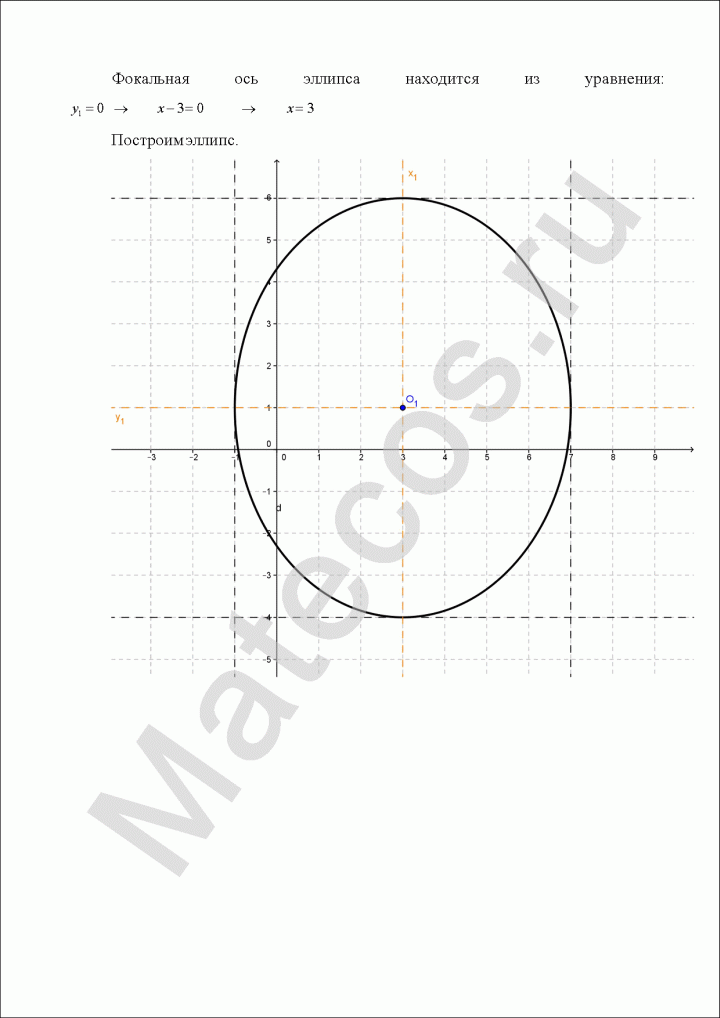
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.
Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.
Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.
Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.
Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.
http://www.evkova.org/krivyie-vtorogo-poryadka
http://www.matburo.ru/ex_ag.php?p1=agk2
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках 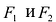
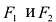
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы 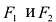
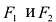
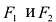
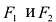
Пусть М(х,у) — произвольная точка эллипса, тогда:
Подставляя сюда значения 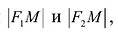
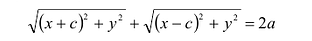
Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим
его:
Возведя обе части уравнения в квадрат и приведя подобные члены, получим:
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 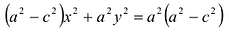
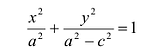
Положительную величину 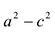
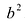
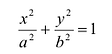
Оно называется каноническим уравнение эллипса.
Координаты точек эллипса ограничены неравенствами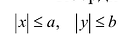
Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки 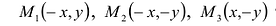
Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:
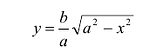
При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.
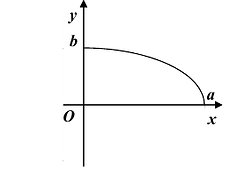
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).
Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии — точка О — центром эллипса. Точки 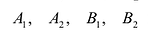
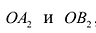
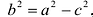
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 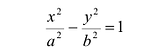
Уравнение (7.6) называется каноническим уравнением гиперболы.
Из уравнения (7.6) видно, что 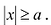
Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
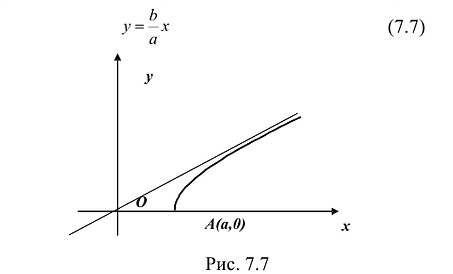
График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты
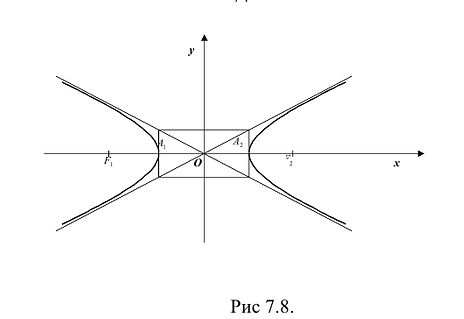
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 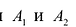
Эксцентриситетом гиперболы называется число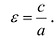
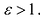
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами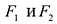
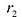
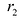
Для правой — ветви 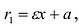
Для левой — ветви
Прямые 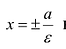
Парабола
Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой 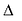
Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе 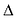
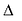
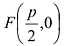
В выбранной системе координат уравнение параболы имеет вид:
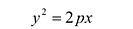
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти 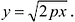
При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10).
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.
Исследование на плоскости уравнения второй степени
Рассмотрим уравнение:
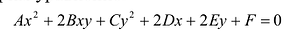
где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) — уравнение второй степени относительно х и у.
Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол
Старые координаты х, у выражаются через новые координаты 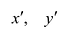
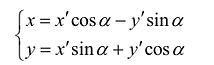
Подставив выражения для х и у в уравнение (8), получим: 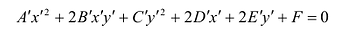
Это уравнение в системе координат 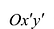
Если в уравнении (7.9) 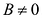
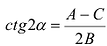
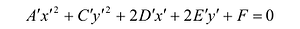
Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:
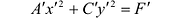
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:
Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.
Кривые второго порядка в высшей математике
Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.
Окружность
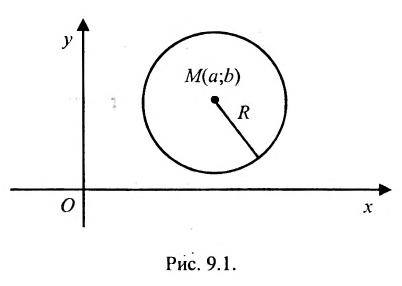
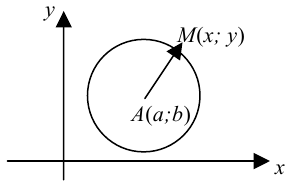
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки — центра окружности.
Если точка 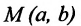
или
Найдём условия, при которых общее уравнение второй степени с двумя переменными
определяет окружность. Раскрыв скобки в (9.1.1), получим
Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,
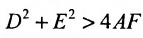
Эллипс
Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.
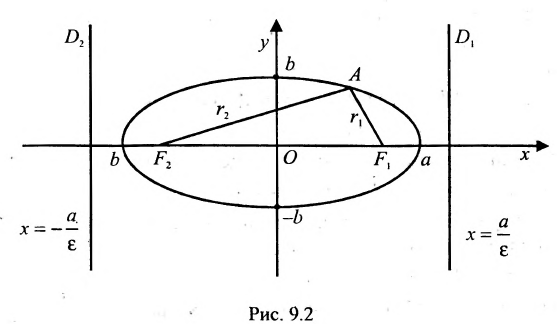
Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами 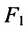
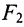
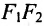
Если точка А — произвольная точка эллипса с координатами (х, у), то
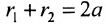
где 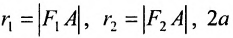
расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 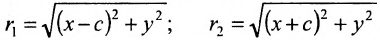
и 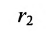
Обе части этого уравнения возведем в квад-Упростив и обозначив
получим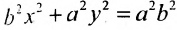
Уравнение (9.2.2) называется каноническим уравнением эллипса, где а — большая полуось, b — малая полуось.
Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет 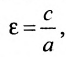
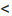
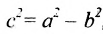
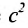
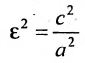
Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше 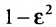
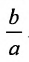
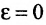
Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 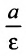
Пример:
Исследовать, какая линия определяется уравнением
Решение:
Сгруппируем члены, содержащие одну и туже переменную, получим
Из второй скобки вынесем коэффициент при 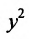
В каждой из скобок выделим полный квадрат
или
Произведём замену: 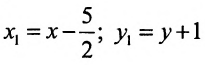
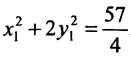
Разделив обе части этого уравнения на 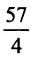
Заданное уравнение определяет эллипс с полуосями 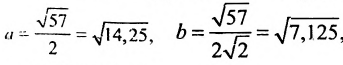
Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку 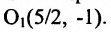
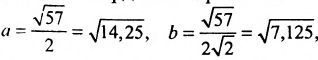
Гипербола
Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению).
Пусть М- произвольная точка гиперболы с фокусами 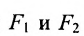
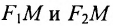
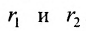
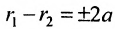
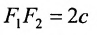
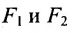
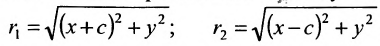
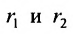
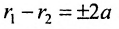
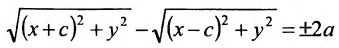
Возведя в квадрат обе части этого уравнения и обозначая 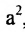
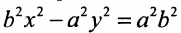
Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 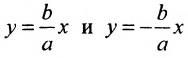
Уравнение вида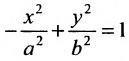
Форму гиперболы характеризует её эксцентриситет 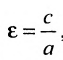
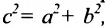
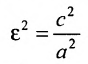
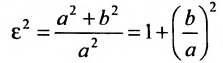
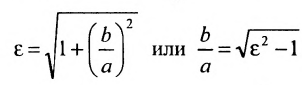
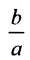
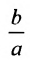
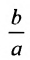
Прямые, заданные уравнениями 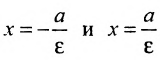
Пример:
Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.
Решение:
В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) — произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи 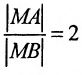
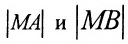
Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:
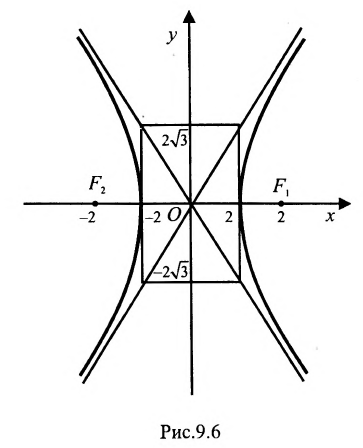
Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая 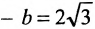
Определим фокусы гиперболы. Для гиперболы выполняется равенство 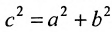
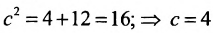
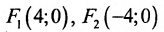
А(4, 0) является правым фокусом гиперболы.
Эксцентриситет полученной гиперболы равен
Подставив значения а и b в уравнения асимптот 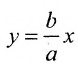
у =—получим уравнения асимптот гиперболы: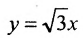
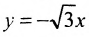
Для построения гиперболы строим основной прямоугольник с полуосями 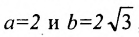
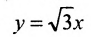
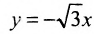
- Заказать решение задач по высшей математике
Парабола
Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).
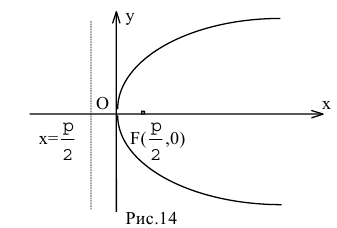
Обозначим фокус параболы — F, расстояние от фокуса до директрисы — р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть 

Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию



Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.
Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и
Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.
Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению
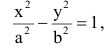
Число а называют действительной полуосью гиперболы, число
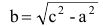
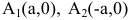
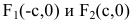
Координатные оси являются осями симметрии гиперболы, а начало координат — ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.
Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 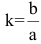
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси:
Эксцентриситет гиперболы изменяется от единицы до бесконечности 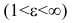
Замечание. Каноническое уравнение 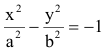
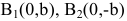
Пример:
Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.
Решение:
Каноническое уравнение гиперболы имеет вид
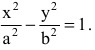
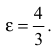
Следовательно, уравнение искомой гиперболы:
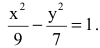
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 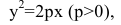
Точка O(0,0) называется вершиной параболы, число р — параметром параболы, 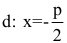
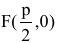
Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид 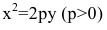
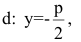
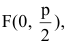
Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:
Пример:
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной
Решение:
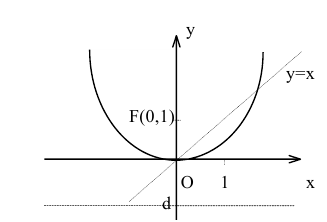
Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:
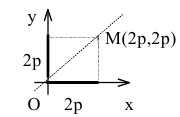
Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений
Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной 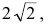
По теореме Пифагора
Тогда искомое уравнение параболы
Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).
Задача решена.
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Числовые множества
- Вектор — определение и основные понятия
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ |
|||||||||||||||||||||
|
Самарский колледж строительства и федерального государственного «Национальный исследовательский |
УЧЕБНО-МЕТОДИЧЕСКОЕ
ПОСОБИЕ
по разделу
Кривые второго порядка
дисциплины
«Математика»
Самара, 2023
|
Одобрена Предметной цикловой Протокол №___ от Председатель ПЦК____________ |
Рассмотрена На заседании Протокол №___ от |
Автор: Буркина Д. Д. преподаватель
высшей квалификационной категории «Самарского колледжа строительства и
предпринимательства (филиал) ФГБОУ ВО «НИ МГСУ».
Учебно-методическое пособие по разделу
«Кривые второго порядка» составлено в соответствии с ФГОС СПО для студентов
второго курса специальностей технического профиля образовательных учреждений
среднего профессионального образования и представляет собой общие рекомендации
по организации лекционных, практических занятий, самостоятельной работы
студентов, проверке качества знаний при изучении раздела «Кривые второго
порядка» в курсе дисциплины «Математика».
Данное пособие содержит теоретические материалы
по разделу «Кривые второго порядка», примеры решения задач по данному разделу,
сборник типовых и дополнительных задач, задание для практической работы в двух
вариантах, контрольный тест, домашнее задание в четырёх вариантах, что является
необходимым для организации аудиторной и внеаудиторной самостоятельной работы
студентов очной и заочной формы обучения.
Материалы предназначены для студентов,
обучающихся по программам среднего профессионального образования, при изучении
раздела «Кривые второго порядка» в курсе высшей математики.
Пособие может быть использовано
преподавателями математики для текущего и рубежного контроля уровня знаний
студентов .
Оглавление
Пояснительная записка
Общее уравнение кривой второго
порадка и его анализ
Кривые второго порядка, их основные
характеристики и параметры
Окружность
Эллипс
Гипербола
Парабола
Построение кривых второго порядка с
помощью циркуля
Построение эллипса
Построение гиперболы
Построение параболы
Примеры решения задач
Сборник задач по кривым второго
порядка
Типовые задачи на приведение
уравнения к каноническому виду и построение кривой
Дополнительные задачи
Практическая работа по разделу
«Кривые второго порядка»
Вариант 1
Вариант 2
Контрольный тест
Домашнее задание
Заключение
Список литературы
Пояснительная записка
Курс геометрии содержит разнообразные
разделы. Если на первом курсе изучались основы стереометрии, векторы в
пространстве, многогранники и круглые тела, то на втором курсе изучается
аналитическая геометрия, кривые и поверхности второго порядка. Понимание теории
и решение задач по геометрии всегда, как в школьном курсе, так и дальше,
вызывают у учащихся затруднения. В данной работе автор представляет своё
видение изложения материала по разделу «Кривые второго порядка» и акцентирует
внимание на практических заданиях, большую часть которых автор разработала
сама.
Учебно-методическое пособие – это один из
видов организационно-инструктивной методической продукции, представляют собой
особым образом структурированную информацию, раскрывающую порядок, логику, акценты
изучения какой-либо темы, раздела или курса, где акцент делается на раскрытии
методики преподавания какой-либо темы или раздела, выработанной на основе
положительного опыта. Задача пособия – рекомендовать наиболее эффективные,
рациональные методы изложения материала, организации аудиторной и
внеаудиторной работы, самостоятельной работы студентов очной и заочной формы
обучения.
Учебно-методическое пособие предназначено
для педагогов и студентов и содержит материалы по методике преподавания и
изучения раздела «Кривые второго порядка» дисциплины «Математика» и методике
выполнения практических работ. Данное пособие может являться
основным учебным пособием по данному разделу дисциплины. Это
средство обучения, предназначенное
для расширения, углубления и лучшего усвоения знаний.
Данное учебно-методическое пособие
содержит три части: теоретическое изложение материала, практикум по решению
задач и материалы для контроля знаний.
Практикум (руководство для проведения
практических занятий) предназначен для закрепления теоретического материала и
проверки знаний. Данный практикум состоит из примеров решения задач по данному
разделу, сборника задач (содержит задачи и методические рекомендации по их
выполнению) и домашних заданий.
Материалы для контроля знаний представлены
в виде заданий для практической работы и контрольного теста.
Актуальность разработки данных
методических рекомендаций состоит в том, что они могут оказать помощь молодым
педагогам и студентам в процессе самостоятельного изучения материала.
Целью составления данного пособия является
оказание методической помощи молодым педагогам, а также помощь студентам в
самостоятельном изучении материала, например, при дистанционном обучении.
Учебно-методическое пособие по разделу
«Кривые второго порядка» разработано в соответствии с ФГОС СПО для студентов
второго курса специальностей технического профиля образовательных учреждений
среднего профессионального образования, содержит как теоретический материал по
разделу «Кривые второго порядка», так и примеры решения типовых задач с
подробным разбором и со всеми сопутствующими математическими выкладками. Практикум
содержит сборник задач для закрепления материала, задания практической работы
по данному разделу в двух вариантах, контрольный тест и домашнее задание.
Лекции содержат все теоретические материалы
по данному разделу и включают определения кривых второго порядка, их
разновидности, канонические уравнения, определения основных параметров и
характеристик, наглядные пояснения, анализ общего уравнения кривой, методы
приведения уравнений к каноническому виду, а также оптические свойства кривых
второго порядка.
В рассмотренных примерах кривая второго
порядка задана общим уравнением. Требуется проанализировать это уравнение,
определив таким образом тип кривой второго порядка и расположение её центра
относительно начала координат. Затем привести уравнение к каноническому виду в
зависимости от типа кривой и построить кривую.
Сборник задач, помогающий студентам лучше
усвоить изложенный материал, кроме задач, в которых нужно привести общее
уравнение к каноническому виду, содержит также другой тип задач, в которых по
каким-то исходным данным (параметрам) нужно составить каноническое уравнение
кривой или найти неизвестную величину (к примеру, расстояние между центрами
двух кривых или расстояние от центра кривой до данной прямой и т.д.). В процессе
решения таких задач студенты учатся понимать не только типичные, но и различные
другие формулировки заданий.
Практическая работа представлена в двух
вариантах и содержит различные задания по данному разделу. Контрольный тест
представлен в одном варианте, домашнее задание – в 4 вариантах.
Задания на построение кривых второго
порядка делятся на две части: математическую, в результате которой уравнение
приводится к каноническому виду и находятся параметры и характеристики кривой,
и чертёжную, в результате которой по найденным параметрам кривая собственно
строится с помощью циркуля и линейки. Интерес студентов вызывает именно
построение кривых второго порядка: эллипса, гиперболы, параболы, за счет чего
осуществляется межпредметная связь с дисциплиной «Инженерная графика».
К. Ф. Гаусс
сказал: «Математика — наука для глаз, а не для ушей», и это действительно так. Студенты
могут проверить своё построение с помощью онлайн-построения графиков, например,
при помощи графического калькулятора Mathway,
задавая онлайн общее уравнение кривой. Также интересным моментом является
демонстрация на занятии анимации построения эллипса; построения эллипса с
помощью нитки, иголок и карандаша; эллипсографа в действии.
К тому же использование
информационных технологий на уроках математики позволяет развивать
межпредметные связи, формировать компьютерную грамотность, развивают
самостоятельность обучающихся во время занятия, облегчает решение задач,
повышает интерес к математике, способствует развитию внимания, памяти,
сообразительности, развивает кругозор.
Настоящее учебное пособие можно
использовать при проведении теоретических, практических занятий, при
самостоятельной работе студентов, при дистанционном обучении, оно будет полезно
для студентов 2 курса СПО при изучении раздела «Кривые второго порядка» в курсе
высшей математики.
Общее уравнение кривой второго порадка и его анализ
Общее уравнение прямой на плоскости – есть
уравнение линейное относительно переменных x
и у
Ах + Ву + С = 0
Общее уравнение кривой 2-го порядка имеет
вид
Ах2 + 2Вху +
Су2 + Dx
+ Ey
+ F
= 0, где
Ах2 + 2Вху + Су2 —
квадратичная часть, Dx
+ Ey
+ F
– линейная часть.
В
дальнейшем будем рассматривать общие уравнения кривых, в которых отсутствует
слагаемое 2Вху, то есть уравнения вида
Ах2 + Су2
+ Dx
+ Ey
+ F
= 0
К
кривым 2-го порядка относятся:
окружность, эллипс,
гипербола, парабола.
Основная задача состоит в умении по общему
уравнению определить тип кривой 2-го порядка, привести уравнение к
каноническому виду и построить кривую в системе координат.
Определение типа кривой 2-го порядка
(анализ общего уравнения):
1.
Если А = С, то уравнение
задаёт окружность.
2.
Если А ≠ С, но А и
С имеют одинаковые знаки, то уравнение задаёт эллипс.
3.
Если А ≠ С, но А и
С имеют разные знаки, то уравнение задаёт гиперболу.
4.
Если А = 0 или С = 0
(то есть отсутствует квадрат одной переменной), то уравнение задаёт параболу.
Если при этом D
= E
= 0 (линейная часть уравнения отсутствует), то
любая кривая будет с центром (вершиной, в случае параболы) в начале координат.
Если же хотя бы один из коэффициентов D
или Е ≠ 0 (наличие линейной части уравнения), то кривая
будет со смещённым центром (вершиной) относительно начала координат.
Приведение уравнения кривой к
каноническому виду и построение
Для построения кривой нужно привести её
общее уравение к каноническому виду, из которого узнать координаты её центра,
основные параметры и вершины.
Чтобы привести уравнение к каноническому
виду в случае, когда центр кривой смещён относительно начала координат, нужно
выделить полные квадраты, используя формулы сокращённого умножения
(a + b)2 = a2 + 2ab
+ b2 и
(a – b)2 = a2 – 2ab + b2
Если в результате получаются выражения
вида (х – х0) и (у – у0), то
центр будет в точке Оꞌ (х0; у0). Для
построения кривой нужно отметить точку Оꞌ и провести
вспомогательную систему координат, о началом в точке Оꞌ. Тогда в
этой новой системе координат кривая будет с центром в начале координат.
Кривые второго порядка, их основные характеристики и
параметры
Окружность
Окружностью
называется множество точек плоскости, равноудаленных от данной точки,
называемой центром окружности, на данном расстоянии, называемом радиусом
окружности.
|
Каноническое уравнение окружности с x2 |
Каноническое уравнение окружности Оꞌ (х0; (x |
Эллипс
Эллипсом
называется множество точек плоскости, сумма расстояний от которых до двух
данных точек, называемых фокусами, есть величина постоянная, равная
длине большей оси.
В общее уравнение эллипса входят квадраты
переменных, при этом коэффициенты перед квадратами разные, но знаки перед ними
одинаковые.
Фокусы эллипса всегда расположены внутри
него и лежат на большой оси.
Эксцентриситетом
эллипса ε называется отношение его фокусного расстояния к длине
большой оси.
Эксцентриситет эллипса можно рассматривать
как меру его вытянутости: чем больше эксцентриситет, тем больше вытянут эллипс.
Директрисы
эллипса – это две прямые d1
и d2,
перпендикулярные к большой оси эллипса, обладающие свойством: отношение
расстояний от любой точки эллипса до фокуса и до соответствующей директрисы
постоянно и равно ε.
1) Каноническое
уравнение эллипса с центром в начале координат О(0; 0) имеет вид

a > b,
то a
– большая полуось, b
– малая полуось
Для любой точки М, лежащей на эллипсе
выполняется условие
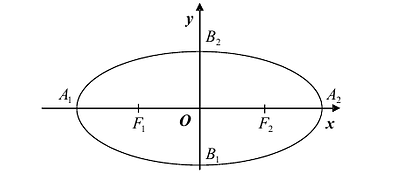
А1 (а; 0), А2
(-а; 0) – вершины на оси Ох, А1
А2 = 2а – большая ось эллипса
В1 (0; b),
В2 (0; —b)
– вершины на оси Оу, B1
B2 = 2b – малая ось эллипса
F1
(c;
0), F2
(-c;
0) – фокусы эллипса на оси Ох,
причем параметр с находится по формуле , F1
F2 = 2c – фокусное расстояние

ε
< 1
, где MF1
— расстояние от точки М эллипса до фокуса, MN
– расстояние от точки М до соответствующей директрисы.
Директрисы d1
и d2
перпендикулярны оси Ох.
Их уравнения d1:
и
d2:
2) Если
a < b,
то a – малая полуось, b
– большая полуось
Для любой точки М, лежащей на эллипсе
выполняется условие

А2 = 2а – малая ось эллипса,
B1
B2 = 2b – большая ось эллипса
F1
(0; с), F2
(0; -с) – фокусы эллипса на оси Оу,
причем параметр с находится по формуле
F1
F2 = 2c – фокусное расстояние
Эксцентриситет ε
< 1
Директрисы d1
и d2
перпендикулярны оси Оy.
Уравнения директрис d1:
и
d2:
3) Каноническое
уравнение эллипса со смещённым центром имеет вид
Точка Оꞌ (х0; у0)
– центр эллипса.
Через точку Оꞌ проводим
вспомогательную систему координат, в которой отмечаем вершины и фокусы эллипса.
4)
Площадь
эллипса вычисляется по формуле , где
a,
b – полуоси эллипса
5)
Оптическое свойство эллипса:
Если в одном из фокусов эллипса расположить источник света, то все лучи,
выходящие из него, после отражения от эллипса концентрируются во втором фокусе.
Гипербола
Гиперболой
называется множество точек плоскости, разность расстояний от которых до двух
данных точек, называемых фокусами,
взятая по абсолютной величине (по модулю), есть величина постоянная, равная
длине действительной оси.
В общее уравнение гиперболы входят
квадраты переменных х и у, при этом коэффициенты
перед квадратами разные и по модулю и по знакам.
Фокусы гиперболы всегда расположены внутри
неё и лежат на действительной оси.
Асимптоты
гиперболы – это прямые, к которым гипебола неограниченно близко приближается,
но никогда их не пересечёт, не коснётся и не разойдётся.
Эксцентриситетом
гиперболы ε называется отношение его фокусного расстояния к длине
действительной оси.
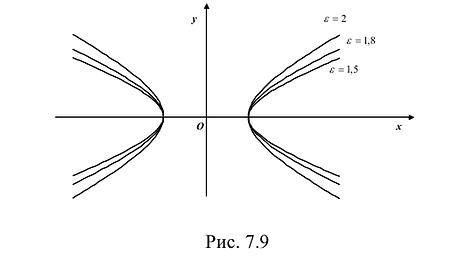
Эксцентриситет гиперболы характеризует
форму гиперболы, степень сжатости её ветвей: чем меньше эксцентриситет, тем
ветви гиперболы более сжаты к действительной оси.
Директрисы
гиперболы – это две прямые d1
и d2,
перпендикулярные к действительной оси гиперболы, обладающие свойством:
отношение расстояний от любой точки гиперболы до фокуса и до соответствующей
директрисы постоянно и равно ε.
Каноническое
уравнение гиперболы с центром в начале координат О(0; 0) имеет
вид
1) Если
перед х2 знак «+», а перед у2
знак «-», то есть уравнение имеет вид

a
– действительная полуось,
b
– мнимая полуось
Для любой точки М, лежащей на гиперболе
выполняется условие
А1 (а; 0), А2
(-а; 0) – действительные вершины гиперболы
на оси Ох, А1 А2 = 2а –
действительная ось
В1 (0; b),
В2 (0; —b)
– мнимые вершины гиперболы на оси Оу, B1
B2 = 2b – мнимая ось
F1
(c;
0), F2
(-c;
0) – фокусы гиперболы на оси
Ох, причем параметр с для любой гиперболы находится по
формуле ,

F2 = 2c – фокусное расстояние
Эксцентриситет ε
> 1
где MF1
— расстояние от точки М эллипса до фокуса,
MN – расстояние от
точки М до соответствующей директрисы.
Директрисы d1
и d2
перпендикулярны оси Ох.
Их уравнения d1:
и
d2:
2)
Построение гиперболы.
Для быстрого построения гиперболы удобно
пользоваться вспомогательными построениями. В системе координат строим
симметричный относительно точки О прямоугольник с размерами 2a×2b
на осях Ох и Оу соответственно. Провести диагонали
этого прямоугольника. Эти диагонали являются асимптотами гиперболы, их
уравнения . На оси Ох отмечаем действительные
вершины А1 и А2 и через них
проводим ветви гиперболы к асимптотам.
Рассмотрим теперь другие виды гипебол.
3) Сопряжённая
гипербола – это гипербола, которая задаётся
уравнением
a
– мнимая полуось, b
– действительная полуось

(а; 0), А2 (-а; 0) – мнимые вершины
на оси Ох, гипербола не пересекается с осью
Ох, расстояние А1 А2 = 2а – мнимая ось гиперболы.
В1 (0; b),
В2 (0; —b)
– действительные вершины на оси Оу, в этих точках
гипербола пересекается с осью Оу, расстояние B1B2
= 2b – действительная ось гиперболы.
F1
(0; с), F2
(0; -с) – фокусы гиперболы на оси Оу,
причем параметр с находится по формуле
с2 = а2 + b2,
F1
F2 = 2c – фокусное расстояние.
Для любой точки М, лежащей на такой гиперболе
выполняется условие
Эксцентриситет ε
> 1
Директрисы d1
и d2
перпендикулярны оси Оy.
Их уравнения d1:
и
d2:
4) 
гипербола – это гипербола, у которой действительная
и мнимая полуоси равны, т.е. a
= b.
Такая гипербола задаётся уравнениями
или
Асимптоты равнобочной гиперболы будут
являться биссектрисами координатных четвертей.

равнобочной гиперболы являются графики функции обратной пропорциональности
5) Каноническое
уравнение гиперболы со смещённым центром имеет вид
или

у0) – центр гиперболы. Через точку Оꞌ проводим
вспомогательную систему координат Оꞌхꞌуꞌ, в которой отмечаем
вершины и фокусы.
Оптическое свойство гиперболы:
лучи, вышедшие из одного фокуса, после
отражения от ближайшей ветви гиперболы, распространяются так, как будто вышли
из другого фокуса.
Парабола
Вспомним, что общее уравнение кривой
второго порядка имеет вид
Ах2 + Су2
+ Dx
+ Ey
+ F
= 0
Если в этом уравнении А
= 0 или С = 0 (то есть
отсутствует квадрат одной переменной), то уравнение задаёт параболу.
Если при этом D
= E
= 0 (линейная часть уравнения отсутствует), то
вершина параболы будет в точке О (в начале координат).
Если же хотя бы один из коэффициентов D
или Е ≠ 0 (наличие линейной части уравнения), то
парабола будет со смещённой вершиной Оꞌ (х0; у0)
относительно начала координат.

плоскости, равноудалённых от данной точки, называемой фокусом
параболы, и от данной прямой, называемой директрисой.
Точка F – фокус, лежит внутри параболы, на
оси симметрии.
Прямая l – директриса, проходит
вне параболы перпендикулярно оси симметрии.
Фокус и директриса лежат по разные стороны
от вершины параболы и отстоят от вершины на расстоянии , где число р –
параметр параболы.
1) Виды
парабол и их канонические уравнения
|
Парабола с вершиной в
фокус директриса |
Парабола с вершиной в
фокус директриса |
|
Парабола с вершиной в
фокус директриса у=- |
Парабола с вершиной в
фокус директриса |
|
Парабола со смещённой вершиной в т. Оꞌ(х0; |
Парабола со смещённой в т. Оꞌ(х0; |
2)
Для
построения параболы нужно знать:
·Координаты её вершины О
(0; 0) или Оꞌ (х0; у0)
·Ось симметрии параболы
(определяется по той переменной, квадрат которой отсутствует в общем уравнении)
·Направление ветвей
(определяется по знаку коффициента 2p в правой части канонического
уравнения: если знак «+», то ветви параболы направлены в положительную сторону,
если знак «–», то в отрицательную)
·Параметр параболы p определяет «ширину» параболы, знание
которой позволяет более качественно построить начальный участок параболы.
3)
Оптическое свойство параболы:
если в фокус параболы
поместить источник света, то все световые лучи после отражения от параболы
будут параллельны оси параболы.
Построение кривых второго порядка с помощью циркуля

кривых второго порядка подсказывают способ их построения с помощью натянутой
нити.
Построение эллипса
Чтобы построить эллипс, нужно сначала его
уравнение привести к каноническому виду, из которого можно найти координаты
вершин эллипса.

дано уравнение эллипса, которое в каноническом виде представляется так:
Построим две концентрические окружности с
центром в начале координат и радиусами a
и b.
Большая из них пересечёт ось абсцисс в вершинах А(-а; 0), В(а; 0),
меньшая пересечёт ось ординат в вершинах С(0; b),
D(0;
—b).
Через точку О проведём пучок прямых,
которые пересекают большую окружность в точках 1, 2, 3, 4,…, а маленькую
окружность в соответствующих точках 1ꞌ, 2ꞌ, 3ꞌ, 4ꞌ,… Через точки 1, 2, 3, 4,…
проводят прямые, параллельные малой оси, а через точки 1ꞌ, 2ꞌ, 3ꞌ, 4ꞌ,… прямые,
параллельные большой оси. Соответствующие пары этих прямых, пересекаясь,
определяют ряд точек. Соединяем эти точки плавной линией, получаем эллипс.
Построение гиперболы
Чтобы построить гиперболу, нужно сначала
её уравнение привести к каноническому виду, из которого можно найти координаты
вершин гиперболы.
Пусть дано уравнение гиперболы, которое в
каноническом виде представляется так:

осях координат строим вершины гиперболы А(-а; 0), В(а; 0), С(0;
b),
D(0;
—b)
и её фокусы F1
(c;
0), F2
(-c;
0). Через вершины А и В
проведём вертикальные прямые, а через вершины С и D
горизонтальные. Эти прямые, пересекаясь, образуют прямоугольник. Проведём
диагонали этого прямоугольника, они будут являться асимптотами гиперболы.

окружности произвольных радиусов r1,
r2,
r3,
… с центром в фокусе F1.
Проведём окружности радиусов r1+2а,
r2+2а,
r3+2а,
… с центром в фокусе F2.
Точки пересечения соответствующих
окружностей принадлежат гиперболе. Соединяя их плавной линией, построим одну
ветвь гиперболы.
Вторую ветвь строим аналогично, поменяв
центры окружностей.
Построение параболы

построить параболу, нужно сначала её уравнение привести к каноническому виду. Пусть
дано уравнение параболы, которое в каноническом виде представляется так:
Отмечаем в системе координат вершину
параболы, фокус и проводим директрису. Вправо от вершины отмечаем ряд произвольных точек 1,
2, 3, 4, 5, 6.
Через
намеченные точки проводим прямые, параллельные директрисе СD, а на них из фокуса F, как из центра радиусом 0-1,
0-2, 0-3, …, 0-6 делаем засечки, пересекающие прямые в
точках I‘=I; II‘=II,
…, VIꞌ=VI. Соединяя полученные точки с вершиной и между
собой плавной линией, получим параболу.
Примеры решения задач

1. Построить кривую x2
+ y2
– 9 = 0
Уравнение кривой второго порядка задано
общим уравнением. При этом коэффициенты А и С
равны. Поэтому это уравнение окружности. Так как линейная часть уравнения
отсутствует, то центр окружности располагается в начале координат – точке О(0;
0). Перенесём 9 в правую часть уравнения
x2
+ y2
= 32
получим сразу каноническое уравнение и строим
окружность с центром О(0; 0) и радиусом R
= 3.

2. Построить кривую
(x
+ 1)2 + (y
– 2)2 = 9
Уравнение уже приведено к каноническому
виду, поэтому определяем, что кривая является окружностью со смещённым центром
в точке Оꞌ(-1; 2) и радиусом R
= 3.
Пример 3.
Построить кривую х2 + у2 – 4x
+ 6y
+ 4 = 0
Уравнение задано в общем виде. Так как А
= С, то это окружность, так как D
≠ 0 и Е ≠ 0 (то
есть в уравнении присутствует линейная часть), то это окружность со смещённым
центром. Приведём уравнение к каноническому виду. Для этого нужно выделить
полные квадраты, используя формулы сокращённого умножения
(a + b)2 = a2 + 2ab
+ b2 и
(a – b)2 = a2 – 2ab + b2
(х2 – 4x)
+ ( у2 + 6y)
+ 4 = 0
(х2 – 4x
+ 4) — 4 + ( у2 + 6y
+ 9) — 9 + 4 = 0
(х – 2)2 – 4 + (у + 3)2
– 9 + 4 = 0
(х – 2)2 + (у + 3)2
= 9 или (х – 2)2 + (у + 3)2
= 32
По каноническому уравнению определяем, что
оно задаёт окружность с центром в т. Оꞌ (2; -3) и радиусом R
= 3.
Пример 4.
Построить кривую 9х2 + 5у2 – 45 = 0
Так как в уравнении коээфициенты при
квадратах переменных х и у разные по модулю и
одинаковых знаков и отсутствует линейная часть, то уравнение задаёт эллипс
с центром в начале координат. Для приведения уравнения к каноническому виду
нужно в правой части уравнения получить 1
9х2 + 5у2
= 45 =˃ =˃
Получили каноническое уравнение эллипса,
из которого находим параметры a
и b
a2 = 5 =˃
a = √5 – малая
полуось
=˃ A1(√5; 0), A2(-√5; 0)
b2
= 9 =˃ b
= 3 — большая полуось =˃ B1(0;
3), B2(0;
-3)

< b
=˃ эллипс
вытянут вдоль оси Оу,
фокусы лежат на оси Оу
c2
= b2
– a2
= 9 – 5 = 4 =˃ c
= 2 =˃
F1(0;
2), F2(0;
-2)
Пример 5.
Построить кривую x2 + 4y2 – 2x + 16y + 1 = 0
Так как в уравнении коээфициенты при
квадратах переменных х и у разные по модулю и
одинаковых знаков и есть линейная часть, то уравнение задаёт эллипс
со смещённым центром относительно начала координат. Для приведения уравнения к
каноническому виду нужно выделить полные квадраты, используя формулы
сокращённого умножения
(a + b)2 = a2 + 2ab
+ b2 и
(a – b)2 = a2 – 2ab + b2
(x2 – 2x) + 4(y2 +
4y) + 1 = 0;
((x2 – 2x + 1) – 1) + 4((y2 +
4y + 4) – 4) + 1 = 0;
(x2 – 2x + 1) – 1 + 4(y2 +
4y + 4) – 16 + 1 = 0;

(x – 1)2 + 4(y + 2)2 =
16,
разделим на 16 обе части уравнения


Получили каноническое уравнение эллипса,
из которого находим центр Оꞌ (1; -2) и параметры a
и b
a2
= 16 =˃ a
= 4 – большая полуось =˃ A1(4;
0), A2(-4;
0)
b2
= 4 =˃ b
= 2 — малая полуось =˃ B1(0;
2), B2(0;
-2)
a
> b
=˃ эллипс
вытянут вдоль оси Ох, фокусы лежат на оси Ох
c2
= a2
– b2
= 16 – 4 = 12 =˃ c
= √12 =˃ F1(√12;
0), F2(-√12;
0)
Пример 6.
Построить кривую 9х2 –
16у2 + 144 = 0
Так как в уравнении коээфициенты при
квадратах переменных х и у разных знаков и
отсутствует линейная часть, то уравнение задаёт гиперболу с
центром в начале координат. Для приведения уравнения к каноническому виду нужно
в правой части уравнения получить 1
9х2 –
16у2 = –
144 =˃
=˃

каноническое уравнение гиперболы, из которого находим параметры a
и b
a2 = 16 =˃
a = 4 – мнимая
полуось
=˃ A1(4; 0), A2(-4; 0)
b2
= 9 =˃ b
= 3 – действ. полуось =˃ B1(0;
3), B2(0;
-3)
фокусы лежат на оси Оу
c2
= a2
+ b2
= 16 + 9 = 25 =˃ c
= 5 =˃ F1(0;
5), F2(0;
-5)
Пример 7.
Построить кривую x2 – y2 + 2x – 4y – 4 = 0
Так как в уравнении коээфициенты при
квадратах переменных х и у имеют разные знаки и
есть линейная часть уравнения, то уравнение задаёт гиперболу со
смещённым центром относительно начала координат. Для приведения уравнения к
каноническому виду нужно выделить полные квадраты, используя формулы
сокращённого умножения
(a + b)2 = a2 + 2ab
+ b2 и
(a – b)2 = a2 – 2ab + b2

– (y2 + 4y) – 4 = 0;
(x2 + 2x + 1 – 1) – (y2 +
4y + 4 – 4) – 4 = 0;
(x2 + 2x + 1) – 1 – (y2 +
4y + 4) + 4 – 4 = 0;
(x + 1)2 – (y + 2)2 – 1 = 0;
(x + 1)2 – (y + 2)2 = 1
Запишем это уравнение в виде

Получили каноническое уравнение гипеболы,
из которого находим центр
Оꞌ (-1; -2) и
параметры a
и b
a2
= 1 =˃ a
= 1 – действительная полуось =˃
A1(1;
0), A2(-1;
0)
b2
= 1 =˃ b
= 1 — мнимая полуось =˃ B1(0;
1), B2(0;
-1)
a
= b
=˃ гипербола
является равнобочной, фокусы лежат на оси Оꞌхꞌ
c2
= a2
+ b2
= 1 + 1 = 2 =˃ c
= √2 =˃ F1(√2;
0), F2(-√2;
0)
Пример 8. Построить кривую y2 – 4x – 4y + 8 = 0
Уравнение кривой задано в общем виде. Так
как отсутствует квадрат переменной х, то уравнение задаёт
параболу с осью симметрии Оꞌхꞌ. Так как в уравнении есть линейная
часть, то вершина параболы будет в точке Оꞌ смещена относительно
начала координат. Найти вершину можно будет после приведения уравнения к
каноническому виду.
Для этого нужно выделить полные квадраты,
используя формулы сокращённого умножения
(a + b)2 = a2 + 2ab
+ b2 и
(a – b)2 = a2 – 2ab + b2

(y2 – 4у) – 4х + 8 = 0
(y2 – 4у + 4) – 4 – 4х + 8 = 0
(у – 2)2 – 4х
+ 4 = 0
(у – 2)2 = 4х
– 4
(у – 2)2 = 4(х
– 1)
Вершина параболы Оꞌ(1;
2)
Ось симметрии Оꞌхꞌ,
ветви направлены в положительную сторону (вправо), 2р = 4 =˃
р = 2 =˃ =˃ фокус
и директриса отстоят от вершины параболы на расстоянии 1.
Сборник задач по кривым второго порядка
Типовые задачи на
приведение уравнения к каноническому виду и построение кривой
Привести
общее уравнение кривой к каноническому виду и построить её.
1) 9х2
– 16у2 – 144 = 0
2) х2
+ 6x
+ 8y
– 31 = 0
3) х2
+ у2 + 10x
– 6y
+ 18
= 0
4) 4х2
+ 9у2 – 36 = 0
5) 4х2
– 5у2 + 80 = 0
6) у2
+ 2х + 8у + 18 = 0
7) 4х2
+ у2 – 9 = 0

– у2 + 4 = 0
9) 4х2
+ 9у2 – 1 = 0
10) х2
– 9у2 + 4 = 0
11) х2
+ у2 – 12х + 35 = 0
12) 4х2
– 3у2 – 12 = 0
13) х2
+ y
– 2 = 0
14) 16х2
+ 7у2 – 64x
+ 42y
+ 15
= 0
15) 5х2
– 3у2 – 10x
– 12y
– 22 = 0
16) 4х2
+ 4у2 – 8x
+ 16y
+ 19
= 0
Дополнительные задачи
1)
Составить уравнение окружности с центром в
точке пересечения прямых 2х + 3у – 13 = 0 и х + у – 5
= 0, если она касается оси ординат.
2)
Составить уравнение прямой, проходящей
через центры двух окружностей х2 + у2 + 4х – 12
= 0 и х2 + у2 – 8у + 7 = 0.
3)
Составить уравнение эллипса с
центром в начале координат, если его большая ось равна 12, фокусы
расположены на оси ординат и фокусное расстояние равно 4√5.
4)
Построить кривые и
5)
Составить уравнение окружности с центром в
точке С (-1; -1), касающейся прямой АВ, если А
(2; -1), В (-1; 3).
6)
Написать уравнение гиперболы и построить
её, если её фокусы находятся в вершинах эллипса 9х2
+ 16у2 – 576 = 0, а вершины в фокусах
этого эллипса.
7) 
определить вид и составить каноническое уравнение кривой второго порядка.

окружности, если известно, что она касается оси абсцисс и прямых х=-1
и х=5.
9) Составить уравнение
окружности, проходящей через точку С(6; 2) с центром в точке Оꞌ(2;
-1).
10) Написать уравнение
окружности, диаметром которой являются две данные точки А(2; 3) и
В(10; 9).
11) Составить уравнение
эллипса с центром в начале координат, если его большая ось по оси Ох равна
10, а эксцентриситет равен 0,6.
12) Составить уравнение
эллипса с центром в начале координат и фокусами, лежащими на оси ординат,
у которого сумма полуосей и фокусное расстояние равно 8.
13) Составить уравнение
гиперболы с центром в начале координат, фокусы которой расположены на
оси абсцисс, если известно, что её действительная ось равна 16, а
эксцентриситет равен 1,25.
14) Составить уравнение
гиперболы с центром в начале координат, фокусы которой расположены на
оси абсцисс, если известно, что мнимая ось равна 12, а фокусное
расстояние раво 16.
15) Составить уравнение
гиперболы с центром в начале координат, фокусы которой расположены на
оси ординат, если известно, что её мнимая ось равна 48, а
уранения асимптот у = ±2,4х.
16) Составить уравнение
гиперболы с центром в начале координат, если известно, что
действительная ось равна 10, а эксцентриситет 1,4.
17) Левая вершина гиперболы с
центром в начале координат находится в точке А(-3; 0), а левый
фокус гиперболы – в точке М(-5; 0). Составить уравнение этой гиперболы,
уравнения её асимптот.
18) Фокусы гиперболы
совпадают с фокусами эллипса 9х2 + 25у2 – 225=0.
Составить уравнение гиперболы, если её эксцентриситет равен 2.
19) Составить уравнение
параболы с вершиной в начале координат, если известно, что она расположена в
левой полуплоскости симметрично относительно оси абсцисс и её параметр равен 5.
20) Составить уравнение
параболы с вершиной в начале координат, если известно, что она симметрична
относительно оси ординат и координаты её фокуса (0; -3).
21) Дан фокус параболы (-3;
-4) и уравнение её директрисы х+1=0. Написать общее
уравнение параболы и найти точки пересечения параболы с осями координат.
Построить параболу.
22) Написать уравнение
параболы, если известно, что вершина параболы находится в точке А(-4; 5),
а её фокус – в точке В(-2; 5). Построить параболу.
Практическая работа по разделу «Кривые второго порядка»
Вариант 1
1.Составьте
уравнение окружности, концы диаметра которой имеют координаты: (0; 3)
и (6; -7).
2.Составьте уравнение окружности, проходящей через начало координат
и имеющей центр в точке с координатами С(-2; 3).
3.Составьте уравнение эллипса, если две его вершины находятся в
точках (0; -8) и (0; 
0) и (5; 0).
4.Составьте уравнение эллипса с фокусами на оси Ох,
если большая ось равна 10, а эксцентриситет равен 0,6.
5.Написать
уравнение гиперболы и ее асимптот, если фокусы гиперболы находятся в
точках F1(4; 0) и
F2(-4;
0), а длина вещественной оси равна 6.
6. 
кривой второго порядка.
7. Привести общее уравнение
кривой второго порядка к каноническому виду и построить её
х2 – у2
+ 16 = 0
9х2 –
16у2 – 576 = 0
х2 + у2
– 8x + 10y + 32 = 0
х2 + у2
+ 2y – 15 = 0
х2 – 4x – 6y – 14 = 0
у2 +
12x – 12 = 0
5х2 +
4у2 – 80 = 0
9х2 + у2
+ 54x – 4y + 67 = 0
Вариант 2
1.
Составьте уравнение
окружности, концы диаметра которой имеют координаты: (-2; 3) и (2;
5).
2.
Составьте уравнение
окружности, проходящей через начало координат и имеющей центр в точке с
координатами С(3; -5).
3.
Составьте уравнение эллипса,
если две его вершины находятся в точках (0; -4) и (0; 4),
а фокусы эллипса в точках (0; -2) и (0; 2).
4.
Составьте уравнение эллипса с
фокусами на оси Ох, если малая ось равна 16, а
эксцентриситет равен 0,6.
5. Написать
уравнение гиперболы и ее асимптот, если фокусы гиперболы находятся в
точках F1(0; 6) и
F2(0;
-6), а длина вещественной оси равна 2√11.
6. 
кривой второго порядка.
7. Привести общее уравнение
кривой второго порядка к каноническому виду и построить её
х2 – у2
– 9 = 0
16х2 –
9у2 + 576 = 0
х2 + у2
+ 6x – 8y = 0
х2 + у2
+ 4х – 5 = 0
у2 – 8x + 2y + 17 = 0
х2 +
6у – 24 = 0
25х2 +
4у2 – 100 = 0
х2 +
4у2 – 8x + 40y + 104 = 0
Контрольный тест
Вопрос
1. Установите соответствия.
|
А) |
1) |
|
Б) |
2) |
|
В) |
3) |
|
Г) Уравнение |
4) |
Правильный
ответ. А – 3, Б – 4, В – 1, Г – 2.
Вопрос
2. Установите соответствия.
|
А) |
1) |
|
Б) |
2) |
|
В) |
3) |
|
Г) |
4) |
Правильный
ответ. А – 4, Б – 1, В – 3, Г – 2.
Вопрос
3. По общему уравнению кривой второго
порядка
Ах2 + Су2 + Dx
+ Ey
+ F
= 0 установите соответствия между значениями
коэффициентов и видом кривой.
|
А) А = |
1) Окружность |
|
Б) А ≠ С, А и С |
2) |
|
В) А = |
3) Эллипс |
|
Г) А ≠ С, А и С |
4) |
Правильный
ответ. А – 1, Б – 3, В – 4, Г – 2.
Вопрос
4. По общему уравнению кривой второго
порядка
Ах2 + Су2 + Dx
+ Ey
+ F
= 0 установите соответствия между значениями
коэффициентов и видом кривой.
|
А) А ≠ С, А и С |
1) |
|
Б) А ≠ С, А и С |
2) |
|
В) А или |
3) |
|
Г) А = 0, Е = 0, |
4) |
Правильный
ответ. А – 2, Б – 4, В – 3, Г – 1.
Вопрос
5. Выберете одну кривую, которая имеет
радиус.
А) Окружность
Б) Эллипс
В) Гипербола
Г) Парабола
Правильный
ответ. А.
Вопрос
6. Выберете одну кривую, которая имеет
асимптоты.
А) Окружность
Б) Эллипс
В) Гипербола
Г) Парабола
Правильный
ответ. В.
Вопрос
7. Выберете одну кривую, которая имеет одну
директрису.
А) Окружность
Б) Эллипс
В) Гипербола
Г) Парабола
Правильный
ответ. Г.
Вопрос
8. Как называется величина р в уравнении
кривой
А) Эксцентриситет
Б) Фокус
В) Параметр
Г) Асимптота
Правильный
ответ. В.
Вопрос
9. Как называется кривая, состоящая из всех
точек плоскости, сумма расстояний от которых до двух данных точек (фокусов)
есть величина постоянная?
А) Окружность
Б) Эллипс
В) Гипербола
Г) Парабола
Правильный
ответ. Б.
Вопрос
10. Как называется кривая, состоящая из всех
точек плоскости, разность расстояний от которых до двух данных точек (фокусов),
взятая по абсолютной величине, есть величина постоянная?
А) Окружность
Б) Эллипс
В) Гипербола
Г) Парабола
Правильный
ответ. В.
Вопрос
11. Как называется кривая, состоящая из всех
точек плоскости, расстояние от которых до данной точки (фокуса) равно
расстоянию до данной прямой (директрисы)?
А) Окружность
Б) Эллипс
В) Гипербола
Г) Парабола
Правильный
ответ. Г.
Вопрос
12. Действительная ось (Оу) и мнимая ось (Ох)
гиперболы равны 8 и 6 соответственно. Каковы
координаты фокусов гиперболы?
А) F1,2
(±5; 0)
Б) F1,2
(0; ±10)
В) F1,2
(0; ±5)
Г) F1,2
(±10; 0)
Правильный
ответ. В.
Вопрос
13. Где находятся фокусы эллипса?
А) На малой оси
внутри эллипса
Б) У эллипса
фокусов нет
В) Снаружи эллипса
на большой оси
Г) Внутри эллипса
на большой оси
Правильный
ответ. Г.
Вопрос
14. Если расстояние от точки, лежащей на
параболе, до фокуса равно 6, то чему равно расстояние от этой
точки до директрисы?
А) 3
Б) 1,5
В) 6
Г) 12
Правильный
ответ. В.
Вопрос
15. По каноническому уравнению кривой
определите её вид
А) Гипербола
Б) Окружность
В) Эллипс
Г) Парабола
Правильный
ответ. Б.
Вопрос
16. По каноническому уравнению кривой
определите её вид
А) Гипербола с
центром в точке Оꞌ(-1; -2)
Б) Гипербола с
центром в точке Оꞌ(1; 2)
В) Эллипс с
центром в точке Оꞌ(1; 2)
Г) Эллипс с
центром в точке Оꞌ(-1; -2)
Правильный
ответ. А.
Вопрос
17. По общему уравнению кривой определите её
вид
х2
– у2 – 9 = 0.
А) Эллипс с
центром в начале координат
Б) Парабола с
вершиной в начале координат
В) Гипербола с
центром в начале координат
Г) Окружность с
центром в начале координат
Правильный
ответ. В.
Вопрос
18. Что нужно поменять в общем уравнении
вопроса №17, чтобы оно задавало окружность?
А) Поменять знак
перед 9 на противоположный
Б) Знак перед у2
поменять на противоположный
В) Все знаки
поменять на противоположные
Г) Все знаки
должны быть положительные
Правильный
ответ. Б.
Вопрос
19. По общему уравнению кривой определите её
вид
х2
+ 6х – у – 4 = 0.
А) Эллипс с
центром в начале координат
Б) Парабола с
вершиной в начале координат
В) Гипербола со
смещённым центром
Г) Парабола со
смещённой вершиной
Правильный
ответ. Г.
Вопрос
20. По общему уравнению кривой определите её
вид
9х2
+ 16у2 – 18х + 64у – 71 = 0.
А) Парабола со
смещённой вершиной
Б) Окружность со
смещённым центром
В) Гипербола со смещённым
центром
Г) Эллипс со
смещённым центром
Правильный
ответ. Г.
Домашнее задание
Домашнее задание №1.
Построить
кривые второго порядка и найти их основные элементы.
А)
Б) В)
Г)
Домашнее задание №2.
Привести
уравнения кривых второго порядка к каноническому виду, построить эти кривые и
найти их основные элементы.
А) х2
+ у2 – 8x + 2y – 23 = 0
Б) 4х2
+ 25у2 – 100 = 0
В)
х2
– 9у2 – 4x – 72y – 149 = 0
Домашнее задание №3.
1. Написать
каноническое и общее уравнение окружности с центром в точке С(2; -3)
и радиусом 6.
2. Привести
уравнение к каноническому виду, построить кривую и найти её основные элементы
х2 + 4у2 + 4x
– 16y
– 4 = 0.
3. Написать уравнение гиперболы, если ее фокусы
находятся в точках F1(4; 0), F2(-4; 0), а длина ее действительной оси равна 6.
Домашнее
задание №4.
1. Найти
центр и радиус окружности
А)
х2 + у2 – 6x
+ 2y
– 26 = 0
Б) 5х2— 10х + 5у2+ 20у — 20 = 0
2. Построить
кривую второго порядка, приведя её уравнение к каноническому виду 4x2 +
9y2 – 144 = 0
3. Построить
кривую второго порядка, приведя её уравнение к каноническому виду x2 –
6x – 10y –
1 = 0
Заключение
Кривые второго порядка были известны еще в
Древней Греции. Тогда они назывались «коническими сечениями», изучению свойств
которых посвящались научные трактаты. Применение изученных греками кривым
нашлось в XVII – XVIII веках в баллистике и астрономии: выяснилось, что
пушечное ядро летит по параболической траектории, а движение планет происходит
по эллиптическим орбитам. Позже в небесной механике были введены понятия
космических скоростей. Оказалось, что тело, запущенное с земной поверхности c
разной начальной скоростью может двигаться в космическом пространстве по
различным траекториям, представляющие собой кривые второго порядка: окружность,
эллипс, параболу, гиперболу. В XX веке многие физические эксперименты показали,
что частицы в этих экспериментах двигаются по траекториям, являющимися кривыми
второго порядка. Например, заряженная частица в однородном электрическом поле
плоского конденсатора движется по параболе, или альфа-частицы в опыте
Резерфорда при рассеивании их ядром атома движутся по гиперболам. В этой связи,
изучение кривых второго порядка в рамках курса высшей математики имеет весьма
важное как теоретическое, так и прикладное значение.
Список литературы
1.
Геометрия. Часть 1. Математика для
техникумов. Под редакцией Г. Н. Яковлева. Издательство «Наука», главная
редакция физико-математической литературы, Москва, 1976
2.
Геометрия. Часть 2. Математика для
техникумов. Под редакцией Г. Н. Яковлева. Издательство «Наука», главная
редакция физико-математической литературы, Москва, 1978
3.
Канатникоа А. Н.: Аналитическая геометрия.
– М.: Академия, 2009
4.
Грешилов А. А.: Аналитическая геометрия.
Векторная алгебра. Кривые второго порядка. – М.: Логос, 2004
Интернет-источники:
5.
https://kvm.gubkin.ru/pub/dlb/metodichka.pdf
6.
https://matecos.ru/mat/matematika/krivye-vtorogo-poryadka.html
7.
https://infourok.ru/prezentaciya-po-matematike-na-temu-krivie-vtorogo-poryadka-501478.html
8.
https://ppt-online.org/284233
9.
https://math.semestr.ru/line/curves-second-order.php
10. https://myslide.ru/presentation/skachat-krivye-i-poverxnosti-vtorogo-poryadka-metodicheskie-materialy
|
|
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.или можно встретить следующую форму записи: К кривым второго порядка относятся окружность, эллипс, гипербола и парабола. |
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ < 0, кривая второго порядка гиперболического типа.
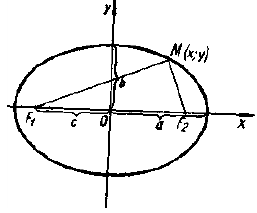
Эллипс — множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 есть величина постоянная, большая расстояния между этими точками.
F1 и F2 — фокусы.
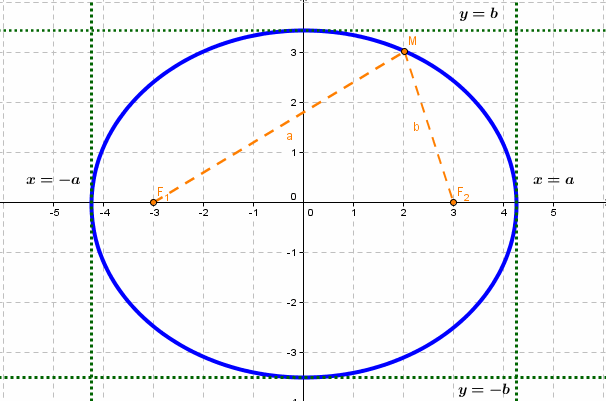 |
с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус. |
Каноническое уравнение эллипса с центром симметрии в начале координат:
2а — большая ось эллипса, 2b — малая ось эллипса.
а — большая полуось эллипса, b — малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
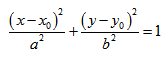
Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
F1 и F2 — фокусы.
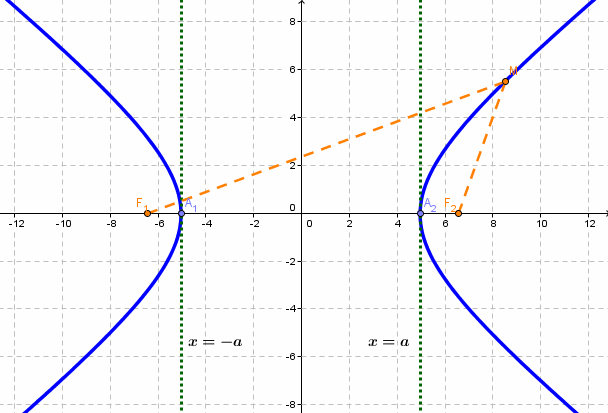 |
с — фокальное расстояние, F1(-c;0) — левый фокус, F2(c;0) — правый фокус. А1(-а;0), А2(а;0) — вершины. |
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:

x — действительная ось, y — мнимая ось.
а — действительная полуось, b — мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 — правая директриса, f2 — левая директриса.
Уравнения директрис:
Порядок построения гиперболы:
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А1(-а;0), А2(а;0).
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
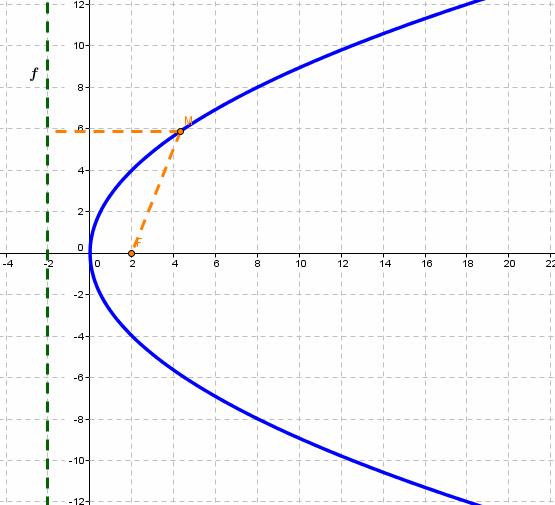 |
р — фокальное расстояние Фокус параболы: Директриса параболы: |
Пример по теме кривые второго порядка №1
Привести к каноническому виду и построить график кривой второго порядка.

Пример по теме кривые второго порядка №2
По виду уравнения определить тип кривой и нарисовать ее в декартовой системе координат:
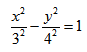
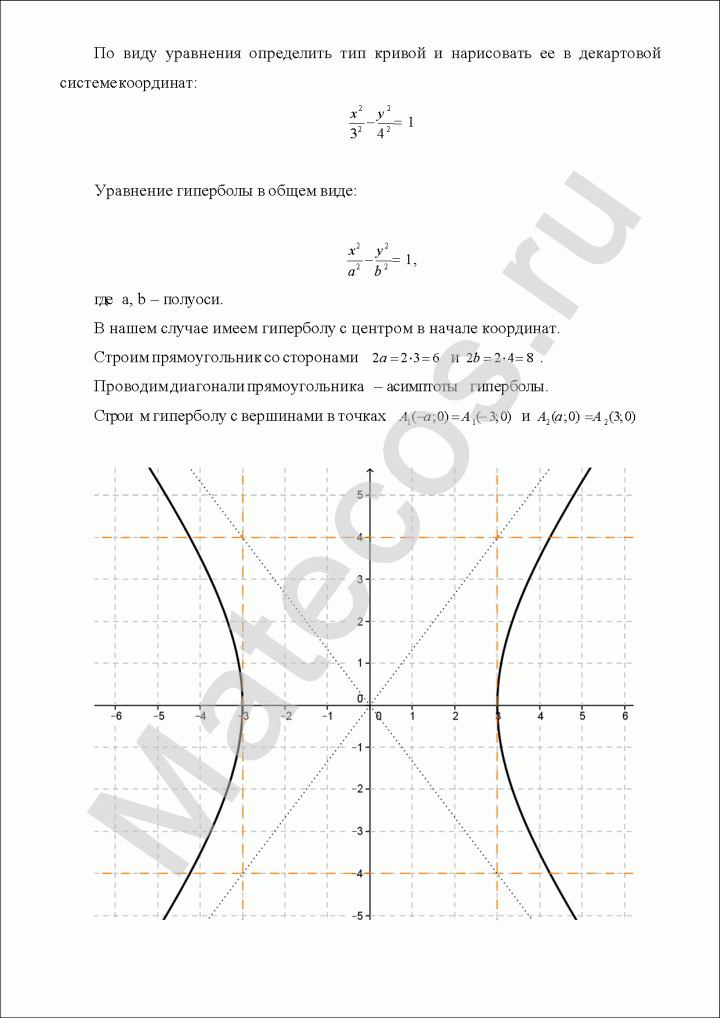
Пример по теме кривые второго порядка №3
Построить кривую второго порядка:
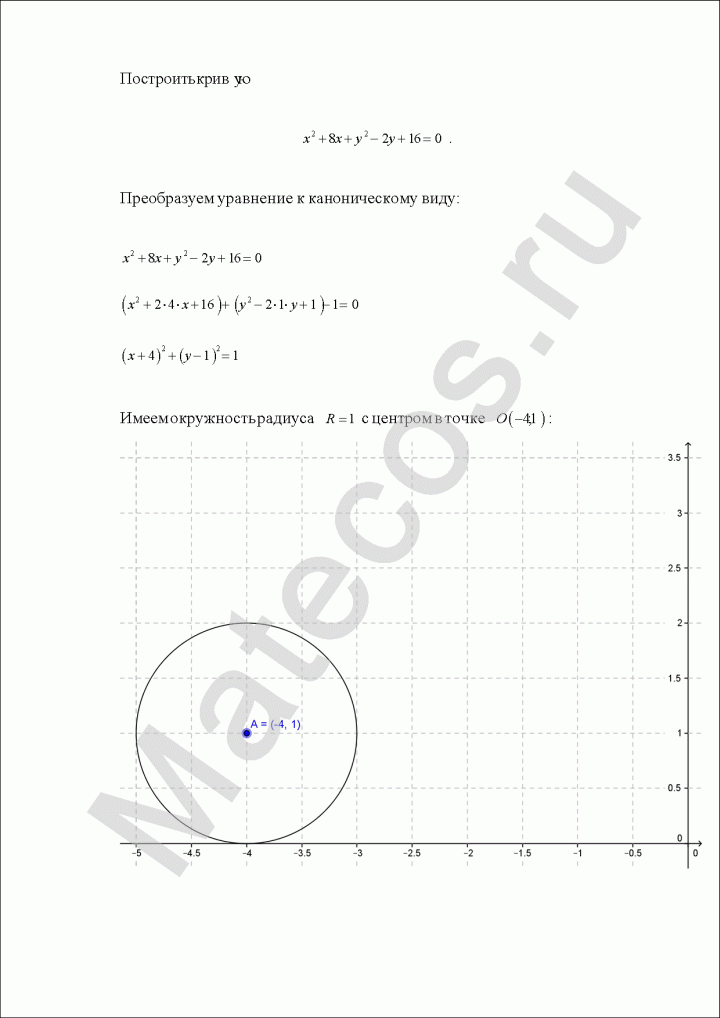
Пример по теме кривые второго порядка №4
Построить кривую второго порядка:
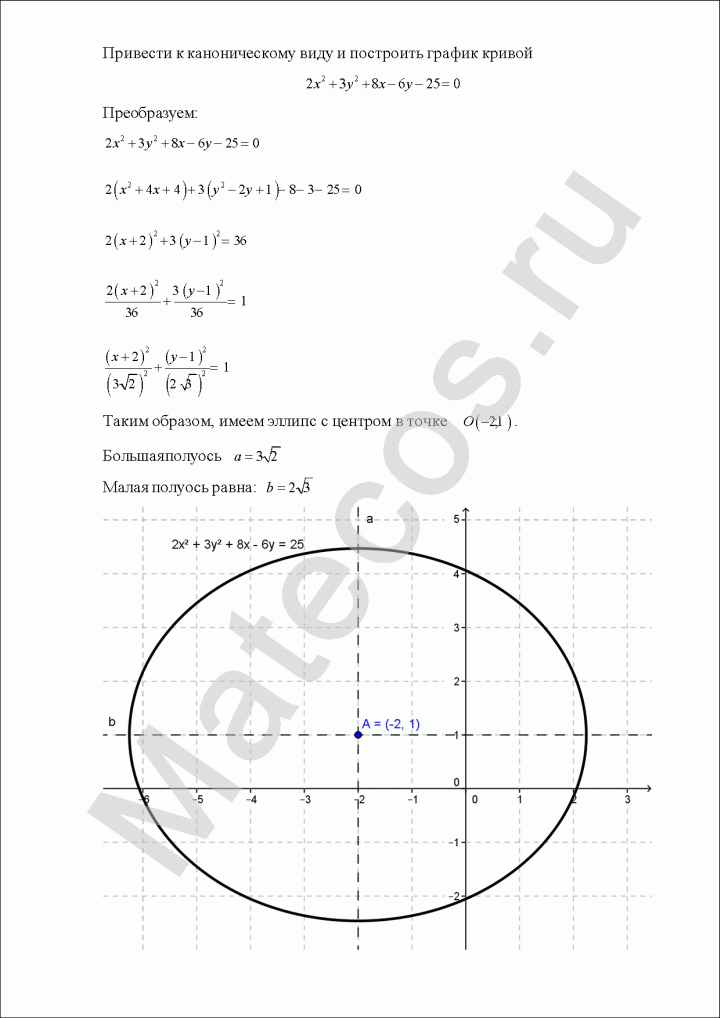
Пример по теме кривые второго порядка №5
Провести заданное уравнение линии второго порядка к каноническому виду и построить ее:

Пример по теме кривые второго порядка №6
Определить центр и радиус окружности:
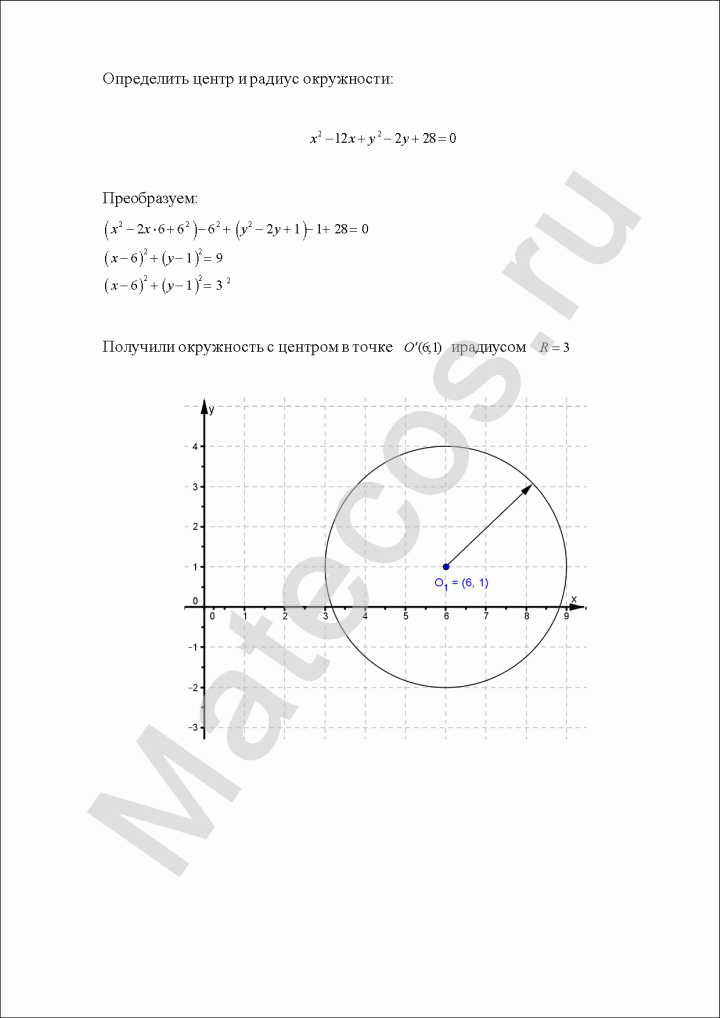
Пример по теме кривые второго порядка №7
Определить центр и полуоси эллипса:
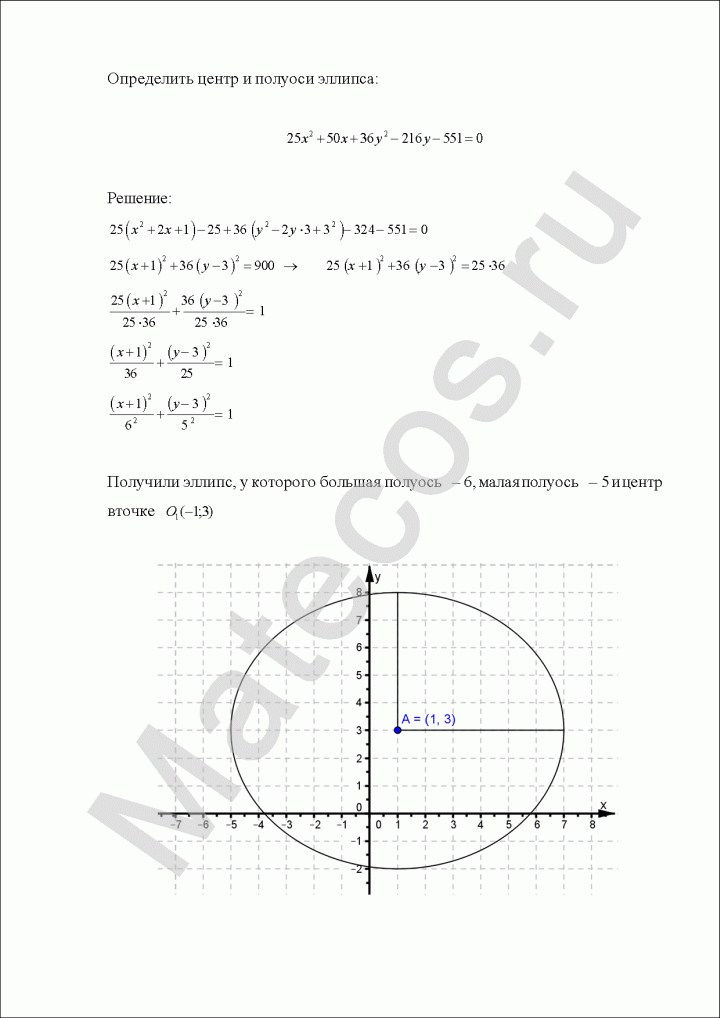
Пример по теме кривые второго порядка №8
Определить центр, полуоси и асимптоты гиперболы:
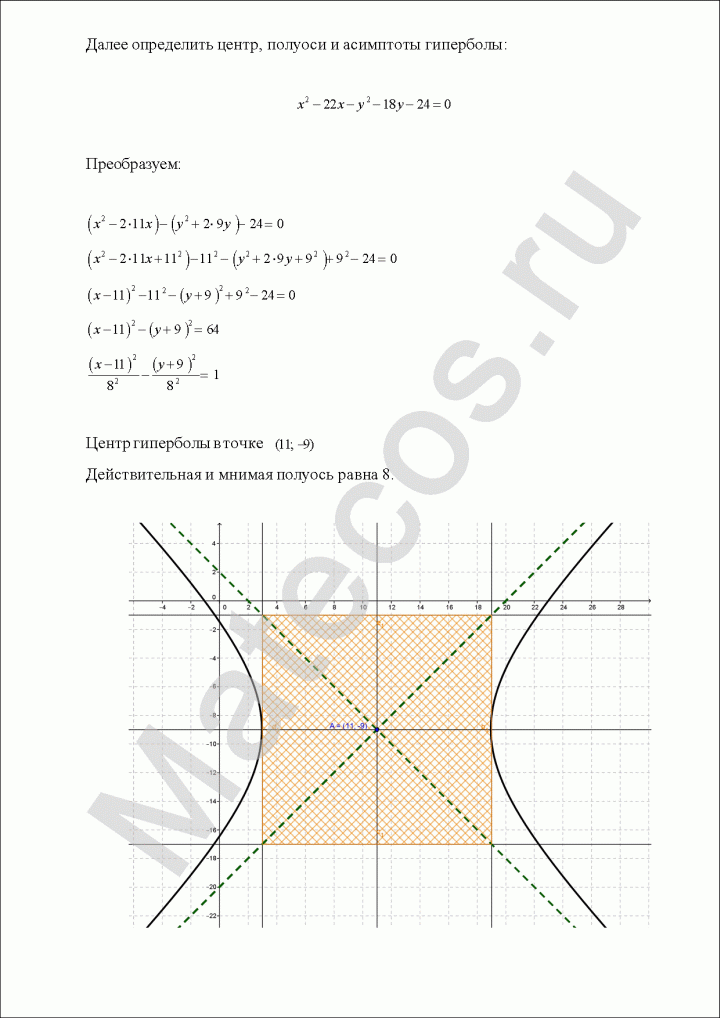
Пример по теме кривые второго порядка №9
Составить уравнение и построить линию, расстояние каждой точки которой от точки A(-1;0) вдвое меньше расстояния ее от прямой x=-4
Пример по теме кривые второго порядка №10
Определить тип кривой второго порядка:
Пример по теме кривые второго порядка №11
Дана кривая:
Докажите, что эта кривая – эллипс.
Найдите координаты центра симметрии.
Найдите его большую и малую полуоси.
Запишите уравнение фокальной оси.
Постройте данную кривую.
Пример по теме кривые второго порядка №12
Дана кривая:
Доказать, что данная кривая – парабола.
Найти координаты вершины параболы.
Найдите значение ее параметра.
Запишите уравнение оси симметрии параболы.
Постройте данную параболу.
Пример по теме кривые второго порядка №13
Дана кривая:
Докажите, что кривая – гипербола.
Найдите координаты центра симметрии гиперболы.
Найдите действительную и мнимую полуоси гиперболы.
Запишите уравнение фокальной оси гиперболы.
Найдите данную гиперболу.
Пример по теме кривые второго порядка №14
Все графике в этой статье были построены в Geogebra.Подробно о построении графиков функции быстрым и удобным способом читать тут:
Кривые линии второго порядка
Общее уравнение кривых второго порядка имеет вид: 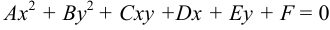
где 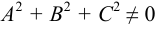
К кривым линиям второго порядка относятся: окружность, эллипс, гипербола и парабола.
Окружность
Окружностью называется множество точек плоскости, равноудаленных от одной и той же точки — центра окружности.
Утверждение. Окружность является кривой второго порядка и ее каноническое уравнение имеет вид:
где 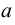
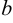
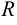
Доказательство. Рассмотрим окружность с заданными параметрами в системе координат на плоскости. Возьмем произвольную точку этой окружности 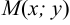
По формуле расстояния между двумя точками имеем:
Возведем обе части уравнения в квадрат и получим
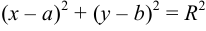
Задача №24.
Показать, что уравнение 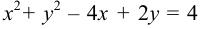
Решение:
Заданное уравнение приведем к виду 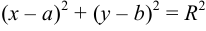
Сгруппируем члены, содержащие только 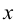
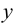
Допишем теперь до квадрата разности и суммы:
Кривая является окружностью с центром 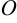
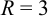
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная равная 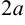
Утверждение. Эллипс является кривой второго порядка, и каноническое уравнение эллипса имеет вид:
где 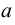
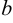
Доказательство. Пусть 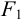
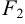
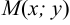
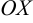
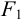
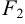
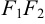
Предположим, что расстояние между фокусами равно 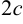
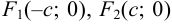
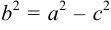
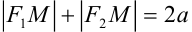
Получаем:
или
Если 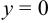
Если 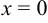
Число 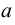
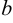
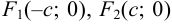
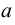
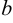
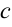
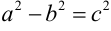
Эксцентриситетом эллипса называется отношение 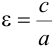
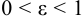
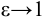
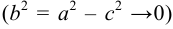
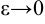
Если 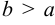
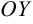
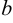
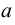
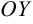
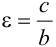
Задача №25.
Найти координаты фокусов эллипса и его эксцентриситет, если известно уравнение эллипса:
Решение:
Уравнение имеет канонический вид и 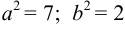
Найдем 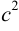
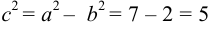
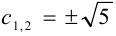
Задача №26.
Показать, что уравнение 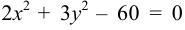
Решение:
Приведем уравнение к каноническому виду:
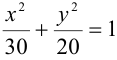
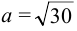
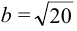
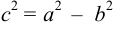
Эксцентриситет
Гипербола
Гиперболой называется множество точек плоскости, абсолютное значение разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
или
Утверждение. Гипербола является кривой второго порядка, и ее каноническое уравнение имеет вид: 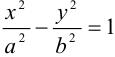
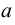
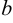
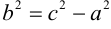
Доказательство. Пусть 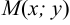
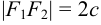
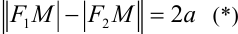
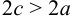
Положим 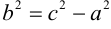
Если 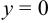
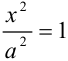
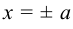
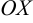
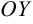
Эксцентриситетом гиперболы называют отношение 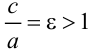
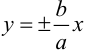
Задача №27.
Составить каноническое уравнение гиперболы, если 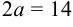
Решение:
Так как 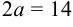
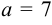
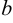
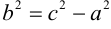
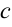
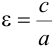
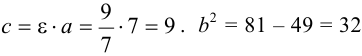
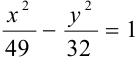
Задача №28.
Показать, что уравнение 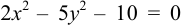
Решение:
Приведем уравнение к каноническому виду:
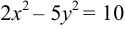
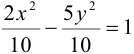
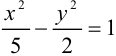
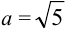
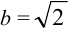
Найдем координаты фокуса. 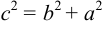
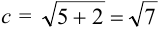
Значит 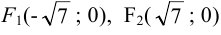
Эксцентриситет
Асимптоты имеют следующие уравнения:
Парабола
Параболой называется множество точек плоскости, каждая из которой одинаково удалена от данной точки 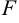
Утверждение. Парабола является кривой второго порядка и ее каноническое уравнение имеет вид: 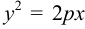
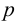
Доказательство. Построим систему координат так, чтобы ось 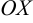
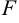
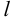
Предположим расстояние 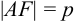
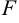
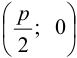
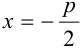
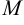
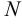
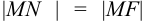
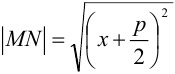
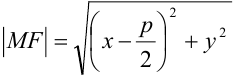
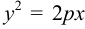
Если 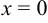
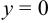
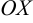
Если 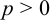
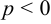
Задача №29.
Найти координаты фокуса и уравнение директрисы следующей параболы 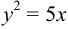
Решение:
Запишем уравнение следующим образом:
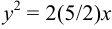
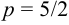
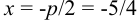
Координаты фокуса: 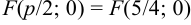
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны: