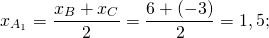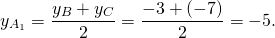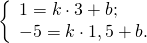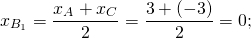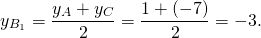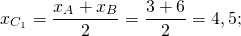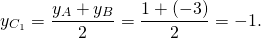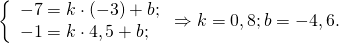Как найти уравнение медианы пространстве

Уравнение медианы треугольника

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

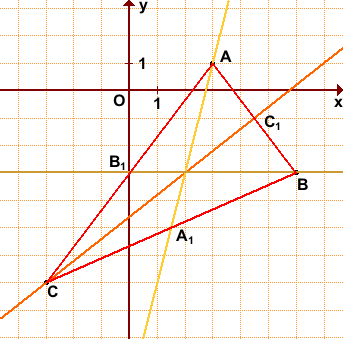
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6ffa0211ace19d45 • Your IP : 178.45.155.83 • Performance & security by Cloudflare

Составить уравнение медианы треугольника проведенной из вершины

УСЛОВИЕ:

5.3.18. Даны вершины треугольника А ( -3 ;2 ;8 ) , B ( -7 ;0 ;3 ) , С (3;4;5).
Составить параметрические уравнения его медианы, проведенной
из вершины А.

РЕШЕНИЕ ОТ u821511235 ✪ ЛУЧШЕЕ РЕШЕНИЕ

Добавил slava191 , просмотры: ☺ 2994 ⌚ 2018-08-23 14:57:00. математика 10-11 класс

Решения пользователей

Написать комментарий

Делим обе части равенства на π

и умножаем на 4

+pi k, k in Z
Можно правую часть записать в виде двух ответов:

x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].

x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]

[b]x=-5 – наибольшее отрицательное [/b]

О т в е т. x=1+8n in Z или x=3+ 8n, n in Z

корни чередуются так:

. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .

[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)

a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член

4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0

5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.

∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.

складываем оба равенства:

2* ∠ А=126 градусов.

По формулам приведения:

sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1

sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1

sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z

Найдем корни, принадлежащие указанному отрезку с помощью неравенства:

-286 ° ≤ 90 ° +360 ° *k ≤ 204 °

-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °

-376 ° ≤ 360 ° *k ≤ 114 °

Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]

Значит, указанному отрезку принадлежат два корня:

x=90 ° +360 °* ([green]-1[/green])=-270 °

x=90 ° +360 °*[red]0[/red]=90 °

7. KT- средняя линия трапеции:

Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)

Высоты треугольников АКО и СОК равны половине высоты трапеции

S_( Δ АКО)+S_( Δ COK)=44

S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=

О т в е т. [b]176[/b]

B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

wolviren

Например, уравнение медианы из вершины [math]A[/math].
Сначала найдите точку [math]A_1[/math] пересечения медианы со стороной [math]BC[/math]

[math]A_1(x_{A_1}, y_{A_1},z_{A_1})= A_1!left(frac{x_B+x_C}{2},, frac{y_B+y_C}{2},, frac{z_B+z_C}{2}right)[/math]

Затем составьте уравнение прямой в пространстве по двум точкам:

[math]AA_1colon~ frac{x-x_A}{x_{A_1}-x_A}= frac{y-y_A}{y_{A_1}-y_A}= frac{z-z_A}{z_{A_1}-z_A}[/math]

то есть нужно просто подставить координаты точек [math]A[/math] и [math]A_1[/math].

Цитата:

а если в координатах дано не 2,а 3 точки А(-3,2,1) В(1,6,3) С(7,0,5). то как найти б) площадь

Запишите векторы

[math]overrightarrow{AB}= {x_B-x_A,, y_B-y_A,, z_B-z_A}=ldots[/math] и [math]overrightarrow{AC}= {x_C-x_A,, y_C-y_A,, z_C-z_A}=ldots[/math],

вычислите их векторное произведение [math]overrightarrow{AB}times overrightarrow{AC}[/math] и воспользуйтесь формулой

[math]S_{triangle ABC}= frac{1}{2}bigl|overrightarrow{AB}times overrightarrow{AC}bigr|[/math]

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Пример.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Решение:

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

1) По формулам координат середины отрезка

   

   

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

   

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

   

   

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы  BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

   

   

C(-3;-7), C(4,5;-1), y=kx+b:

   

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.