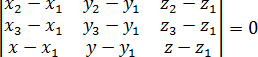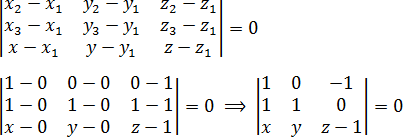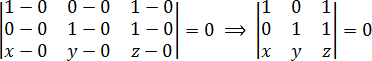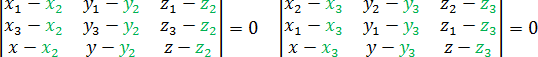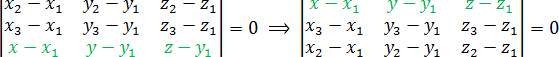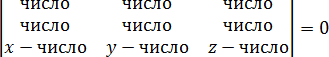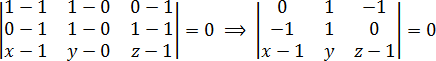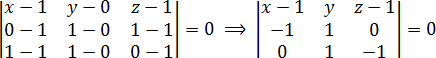23 ноября 2012
В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.
Уравнение плоскости по трем точкам
Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:
Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3);Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:
Ax + By + Cz + D = 0
где числа A, B, C и D — коэффициенты, которые, собственно, и требуется найти.
Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Ax + By + Cz + D = 0. Получится система из трех уравнений, которая легко решается.
Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.
Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием без каких-либо обоснований и доказательств.
Уравнение плоскости через определитель
Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.
Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: M = (x1, y1, z1); N = (x2, y2, z2); K = (x3, y3, z3). Тогда уравнение этой плоскости можно записать через определитель:

Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:
Задача. Составьте уравнение плоскости, проходящей через точки:
A1 = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);
Составляем определитель и приравниваем его к нулю:
Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные x, y и z шли в правильной последовательности. Вот и все! Уравнение плоскости готово!
Задача. Составьте уравнение плоскости, проходящей через точки:
A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);
Сразу подставляем координаты точек в определитель:
Снова раскрываем определитель:
a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − (x + y) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;
Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, но все-таки рекомендуется — чтобы упростить дальнейшее решение задачи.
Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.
На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит x2 или x3, а в какой — просто x. Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.
Откуда берется формула с определителем?
Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.
Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3).
Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:
T = (x, y, z)
Берем любую точку из первой тройки (например, точку M) и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:
MN = (x2 − x1, y2 − y1, z2 − z1);
MK = (x3 − x1, y3 − y1, z3 − z1);
MT = (x − x1, y − y1, z − z1).
Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:
Эта формула означает, что объем параллелепипеда, построенного на векторах MN, MK и MT, равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка T = (x, y, z) — как раз то, что мы искали.
Замена точек и строк определителя
У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:
Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки T = (x; y; z) в самом верху. Пожалуйста, если вам так удобно:
Некоторых смущает, что в одной из строчек присутствуют переменные x, y и z, которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:
Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:
Ax + By + Cz + D = 0
Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.
Задача. Составьте уравнение плоскости, проходящей через точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1).
Итак, рассматриваем 4 точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1);
T = (x, y, z).
Для начала составим стандартный определитель и приравниваем его к нулю:
Раскрываем определитель:
a = 0 · 1 · (z − 1) + 1 · 0 · (x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · (x − 1) + 1 · (−1) · (z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;
Все, мы получили ответ: x + y + z − 2 = 0.
Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными x, y, z не внизу, а вверху:
Вновь раскрываем полученный определитель:
a = (x − 1) · 1 · (−1) + (z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) · 1 · 0 + y · (−1) · (−1) + (x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;
Мы получили точно такое же уравнение плоскости: x + y + z − 2 = 0. Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.
Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.
В рассмотренной выше задаче мы использовали точку B1 = (1, 0, 1), но вполне можно было взять C = (1, 1, 0) или D1 = (0, 1, 1). В общем, любую точку с известными координатами, лежащую на искомой плоскости.
Смотрите также:
- Видеоурок по задачам C2: уравнение плоскости через определитель
- Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
- Тест к уроку «Что такое числовая дробь» (легкий)
- Сводный тест по задачам B15 (1 вариант)
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: тарифы на сотовую связь
Описание презентации по отдельным слайдам:
-
1 слайд
С использованием матриц
Уравнение плоскости
по трем точкам
Котова И. Е. МАОУ СОШ №2
Имени Н. А. Тимофеева
г.о. Бронницы -
2 слайд
Что такое матрица и определитель
Матрица — это просто таблица, заполненная числами. Матрицы бывают квадратными (когда количество строк совпадает с количеством столбцов) и прямоугольными (когда не совпадает);
Определитель — это число, которое находится по специальному алгоритму из чисел, записных в квадратной матрице. У каждого размера матрицы свой алгоритм. Для прямоугольных матриц определитель найти нельзя. -
3 слайд
Квадратные матрицы
-
4 слайд
Прямоугольные матрицы
-
5 слайд
Как считать определитель 3-го порядка
-
6 слайд
Что это за пентаграммы?
На первом рисунке мы берем три числа, лежащие на диагонали, и перемножаем их. Затем берем другие тройки чисел, лежащие в вершинах треугольников, и тоже перемножаем их между собой. В результате всех этих действий мы получим три числа, которые надо сложить (поэтому внизу левой картинки стоит знак плюс).
Теперь разбираемся со второй картинкой. Здесь мы снова берем и перемножаем три числа, но уже на другой диагонали. Так же мы снова берем два треугольника и перемножаем числа, стоящие в их углах (отдельно для каждого треугольника). Полученные три числа опять складываем, а результат вычитаем из первого числа (поэтому внизу справа стоит знак минус). -
7 слайд
Вычислить определитель
1 · 5 · 9 = 45
2 · 6 · 7 = 84;
3 · 4 · 8 = 96.
45 + 84 + 96 = 225
3 · 5 · 7 = 105
2 · 4 · 9 = 72;
1 · 6 · 8 = 48;
105 + 72 + 48 = 225
=225 − 225 = 0. -
8 слайд
Вычислить определитель
-
9 слайд
Уравнение плоскости
Ax + By + Cz + D = 0
Плоскость задается тремя точками
А(х1;у1;z1) В(х2;у2;z2) С(х3;у3;z3)
Т(х; у;z) точка с произвольными координатами. Принадлежащая этой плоскости -
10 слайд
Проведем векторы и найдем их координаты
-
11 слайд
Составляем квадратную матрицу
Так как вектора лежат в одной плоскости, определитель равен нулю. -
12 слайд
Составить уравнение плоскости, проходящей через три точки
A1 = (0, 0, 1);
B1 = (1, 0, 0);
C1 = (1, 1, 1); -
13 слайд
Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
-
14 слайд
Написать уравнение плоскости, проходящей через точки
-
15 слайд
х
у
z
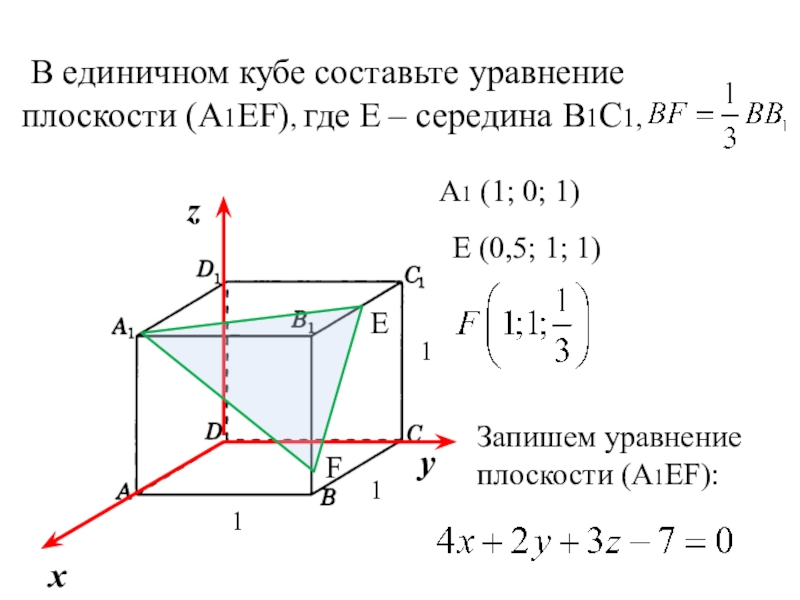
В единичном кубе составьте уравнение плоскости (А1EF), где Е – середина В1С1,
1
1
1
F
E
A1 (1; 0; 1)
Е (0,5; 1; 1)
Запишем уравнение плоскости (А1EF): -
16 слайд
х
y
z
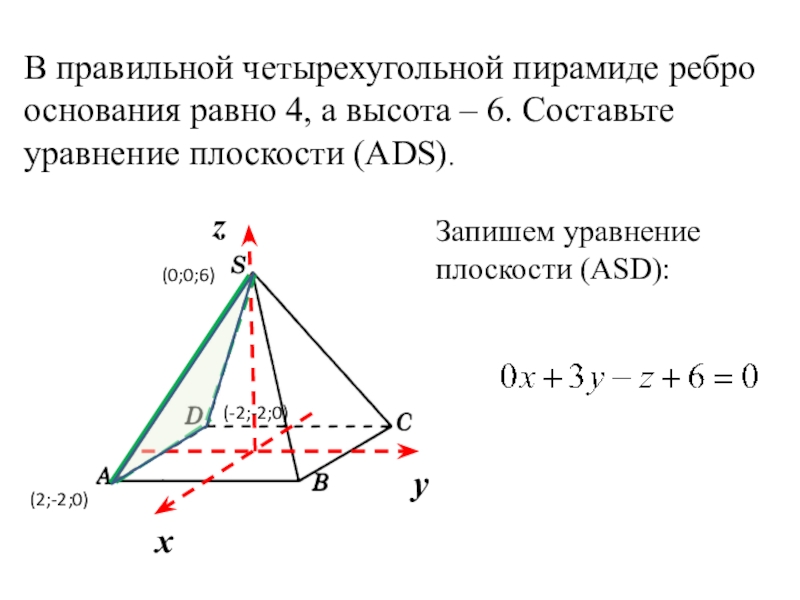
В правильной четырехугольной пирамиде ребро основания равно 4, а высота – 6. Составьте уравнение плоскости (АDS).
Запишем уравнение плоскости (АSD):
(2;-2;0)
(-2;-2;0)
(0;0;6)
Слайд 1
С использованием матриц Уравнение плоскости по трем точкам Котова И. Е. МОУ СОШ №2 г. Бронницы
Слайд 2
Что такое матрица и определитель Матрица — это просто таблица, заполненная числами. Матрицы бывают квадратными (когда количество строк совпадает с количеством столбцов) и прямоугольными (когда не совпадает); Определитель — это число, которое находится по специальному алгоритму из чисел, записных в квадратной матрице. У каждого размера матрицы свой алгоритм. Для прямоугольных матриц определитель найти нельзя.
Слайд 3
Квадратные матрицы
Слайд 4
Прямоугольные матрицы
Слайд 5
Как считать определитель 3-го порядка
Слайд 6
Что это за пентаграммы? На первом рисунке мы берем три числа, лежащие на диагонали, и перемножаем их. Затем берем другие тройки чисел , лежащие в вершинах треугольников, и тоже перемножаем их между собой. В результате всех этих действий мы получим три числа, которые надо сложить (поэтому внизу левой картинки стоит знак плюс). Теперь разбираемся со второй картинкой. Здесь мы снова берем и перемножаем три числа, но уже на другой диагонали. Так же мы снова берем два треугольника и перемножаем числа, стоящие в их углах (отдельно для каждого треугольника). Полученные три числа опять складываем, а результат вычитаем из первого числа (поэтому внизу справа стоит знак минус).
Слайд 7
Вычислить определитель 1 · 5 · 9 = 45 2 · 6 · 7 = 84; 3 · 4 · 8 = 96. 45 + 84 + 96 = 225 3 · 5 · 7 = 105 2 · 4 · 9 = 72; 1 · 6 · 8 = 48; 105 + 72 + 48 = 225 =225 − 225 = 0.
Слайд 8
Вычислить определитель
Слайд 9
Уравнение плоскости Ax + By + Cz + D = 0 Плоскость задается тремя точками А(х 1 ;у 1 ; z 1 ) В(х 2 ;у 2 ; z 2 ) С(х 3 ;у 3 ; z 3 ) Т(х; у; z) точка с произвольными координатами , принадлежащая этой плоскости.
Слайд 10
Проведем векторы и найдем их координаты
Слайд 11
Составляем квадратную матрицу Так как вектора лежат в одной плоскости, определитель равен нулю.
Слайд 12
Составить уравнение плоскости, проходящей через три точки A 1 = (0, 0, 1); B 1 = (1, 0, 0); C 1 = (1, 1, 1);
Слайд 13
Раскрываем определитель : a = 1 · 1 · ( z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y; b = (−1) · 1 · x + 0 · 1 · ( z − 1) + 1 · 0 · y = −x; d = a − b = z − 1 − y − (− x ) = z − 1 − y + x = x − y + z − 1; d = 0 ⇒ x − y + z − 1 = 0;

1. Общее уравнение плоскости
Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0 , где А, В, С – координаты вектора
N = Ai + Bj + Ck -вектор нормали к плоскости. Возможны следующие частные случаи:
A = 0 – плоскость параллельна оси Ох
B = 0 – плоскость параллельна оси Оу C = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
A = B = 0 – плоскость параллельна плоскости хОу A = C = 0 – плоскость параллельна плоскости хОz B = C = 0 – плоскость параллельна плоскости yOz A = D = 0 – плоскость проходит через ось Ох
B = D = 0 – плоскость проходит через ось Оу C = D = 0 – плоскость проходит через ось Oz
A = B = D = 0 – плоскость совпадает с плоскостью хОу A = C = D = 0 – плоскость совпадает с плоскостью xOz B = C = D = 0 – плоскость совпадает с плоскостью yOz
2. Уравнение поверхности в пространстве
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
3. Уравнение плоскости, проходящей через три точки
Для того, чтобы через три какиелибо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе
|
координат. |
||||||
|
Для того, чтобы произвольная точка M (x, y, z) |
лежала в одной плоскости с точками |
|||||
|
M1, M2 , M3 необходимо, чтобы векторы M1M 2 , M1M 3 , M1M были компланарны, т.е |
||||||
|
M1M = {x − x1 ; y − y1 ; z − z1} |
||||||
|
( M1M 2 , M1M 3 , M1M ) = 0. Таким образом, M1M 2 |
= {x2 − x1 ; y2 |
− y1 ; z2 − z1} |
||||
|
M1M 3 |
= {x3 − x1 ; y3 − y1 ; z3 − z1} |
|||||
|
x − x1 |
y − y1 |
z − z1 |
||||
|
Уравнение плоскости, проходящей через три точки: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
35

4. Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости
Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и векторa = (a1, a2 , a3 ) .
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную
|
точку М(х, у, z) параллельно вектору a . |
||||||||||
|
Векторы M1M = {x − x1 ; y − y1 ; z − z1} |
и вектор a = (a , a |
2 |
, a |
3 |
) |
должны быть |
||||
|
M1M 2 = {x2 − x1 ; y2 − y1 ; z2 − z1} |
1 |
|||||||||
|
x − x1 |
y − y1 |
z − z1 |
||||||||
|
компланарны, т.е. ( M1M , M1M 2 , a ) = 0.Уравнение плоскости: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||||||
|
a1 |
a2 |
a3 |
5. Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости
Пусть заданы два вектора a = (a1, a2 , a3 ) и b = (b1,b2 ,b3 ) , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы a,b, MM1 должны быть компланарны.
|
x − x1 |
y − y1 |
z − z1 |
|||
|
Уравнение плоскости: |
a1 |
a2 |
a3 |
= 0 . |
|
|
b1 |
b2 |
b3 |
6. Уравнение плоскости по точке и вектору нормали
Теорема. Если в пространстве задана точка M0 (x0 , y0 , z0 ) , то уравнение плоскости, проходящей через точку M0 перпендикулярно вектору нормали N ( A, B,C) имеет вид: A(x − x0 ) + B ( y − y0 ) + C (z − z0 ) = 0 .
7. Уравнение плоскости в отрезках
Если в общем уравнении Ax + By + Cz + D = 0 поделить обе части на (-D)
|
− |
A |
x − |
B |
y − |
C |
z − 1 = 0 , заменив − |
D |
= a, |
− |
D |
= b, |
− |
D |
= c , получим уравнение плоскости |
||||||||
|
A |
B |
C |
||||||||||||||||||||
|
D |
D |
D |
||||||||||||||||||||
|
в отрезках: |
x |
+ |
y |
+ |
z |
= 1 . Числа a, b, c являются точками пересечения плоскости соответственно |
||||||||||||||||
|
a |
b |
c |
||||||||||||||||||||
с осями х, у, z.
8. Уравнение плоскости в векторной форме
r n = p, где r = xi + yj + zk — радиусвектор текущей точки M (x, y, z) ,
n = i cosα + j cos β + k cosγ — единичный вектор, имеющий направление, перпендикуляра,
опущенного на плоскость из начала координат. α, β и γ — углы, образованные этим вектором с осями х, у, z. p – длина этого перпендикуляра. В координатах это уравнение имеет вид:
x cosα + y cos β + z cosγ − p = 0
36
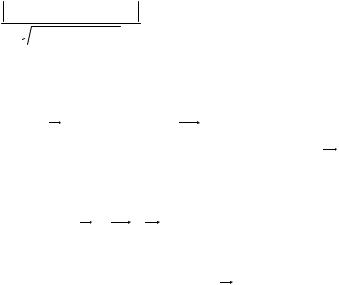
9. Расстояние от точки до плоскости
Расстояние от произвольной точки M0 (x0 , y0 , z0 ) до плоскости Ax + By + Cz + D = 0 равно:
d = Ax0 + By0 + Cz0 + D

Пример. Найти уравнение плоскости, проходящей через точки А(2,-1,4) и В(3,2,-1) перпендикулярно плоскости x + y + 2z − 3 = 0 .
Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0 , вектор нормали к этой плоскости n1 (A,B,C). Вектор AB (1,3,-5) принадлежит плоскости. Заданная нам плоскость,
перпендикулярная искомой имеет вектор нормали n2 (1,1,2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то
|
n = AB × n |
i |
j |
k |
= i |
3 |
− 5 |
− j |
1 |
− 5 |
+ k |
1 |
3 |
= 11i − 7 j − 2k. |
||||||||
|
2 |
= |
1 |
3 |
− 5 |
|||||||||||||||||
|
1 |
1 |
2 |
1 |
2 |
1 |
1 |
|||||||||||||||
|
1 |
1 |
2 |
|||||||||||||||||||
Таким образом, вектор нормали n1 (11,-7,-2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е.
11.2+ 7.1− 2.4 + D = 0; D = −21. Итого, получаем уравнение плоскости: 11x − 7 y − 2z − 21 = 0
10.Уравнение линии в пространстве
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0 . Это уравнение называется уравнением линии в пространстве.
Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана какимлибо уравнением.
Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.
F(x, y, z) = 0
Тогда пару уравнений Ф(x, y, z) = 0 назовем уравнением линии в пространстве.
11. Уравнение прямой в пространстве по точке и направляющему вектору
Возьмем произвольную прямую и вектор S (m, n, p), параллельный данной прямой. Вектор S называется направляющим вектором прямой.
На прямой возьмем две произвольные точки M0 (x0 , y0 , z0 ) и M (x, y, z) .
z
37
z
S M1
M0
r0 r
Обозначим радиусвекторы этих точек как r0 и r , очевидно, что r − r0 = M0 M .
Т.к. векторы М0 М и S коллинеарны, то верно соотношение М0 М = St , где t – некоторый параметр. Итого, можно записать: r = r0 + St .
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
x = x0 + mt
Это векторное уравнение может быть представлено в координатной форме: y = y0 + nt
z = z0 + pt
Преобразовав эту систему и приравняв значения параметра t, получаем канонические
|
уравнения прямой в пространстве: |
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
m |
n |
|||||
|
p |
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора S , которые могут быть вычислены по формулам:
|
cosα = |
m |
; cos β = |
n |
; cosγ = |
p |
. |
||
|
+ n2 |
+ p2 |
+ n2 + p2 |
m2 + n2 + p2 |
|||||
|
m2 |
m2 |
Отсюда получим: m : n : p = cosα : cos β : cosγ .
Числа m , n , p называются угловыми коэффициентами прямой. Т.к. S — ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
12. Уравнение прямой в пространстве, проходящей через две точки
Если на прямой в пространстве отметить две произвольные точки M1 (x1, y1, z1 ) и
M2 (x2 , y2 , z2 ), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
|
x2 − x1 |
= |
y2 − y1 |
= |
z2 − z1 |
. |
|
m |
n |
||||
|
p |
38
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Составить уравнение плоскости с помощью матриц
Содержание
-
1.
Составить уравнение плоскости с помощью матриц -
2.
Что такое матрица и определительМатрица — это просто -
3.
Квадратные матрицы -
4.
Прямоугольные матрицы -
5.
Как считать определитель 3-го порядка -
6.
Что это за пентаграммы? На первом рисунке -
7.
Вычислить определитель1 · 5 · 9 = -
8.
Вычислить определитель -
9.
Уравнение плоскостиAx + By + Cz + D = 0Плоскость задается тремя точкамиА(х1;у1;z1) -
10.
Проведем векторы и найдем их координаты -
11.
Составляем квадратную матрицуТак как вектора лежат в одной плоскости, определитель равен нулю. -
12.
Составить уравнение плоскости, проходящей через три точкиA1 = -
13.
Раскрываем определитель:a = 1 · 1 · (z − -
14.
Написать уравнение плоскости, проходящей через точки -
15.
В единичном кубе составьте уравнение плоскости -
16.
В правильной четырехугольной пирамиде ребро основания равно
Что такое матрица и определительМатрица — это просто таблица, заполненная числами. Матрицы бывают квадратными (когда количество строк совпадает с количеством столбцов) и прямоугольными (когда не совпадает);Определитель — это число, которое находится по специальному алгоритму из чисел, записных в
Слайд 1С использованием матриц
Уравнение плоскости
по трем точкам
Котова И. Е. МАОУ СОШ
№2
Имени Н. А. Тимофеева
г.о. Бронницы

Слайд 2Что такое матрица и определитель
Матрица — это просто таблица, заполненная числами. Матрицы
бывают квадратными (когда количество строк совпадает с количеством столбцов) и прямоугольными (когда не совпадает);
Определитель — это число, которое находится по специальному алгоритму из чисел, записных в квадратной матрице. У каждого размера матрицы свой алгоритм. Для прямоугольных матриц определитель найти нельзя.

Слайд 5Как считать определитель 3-го порядка
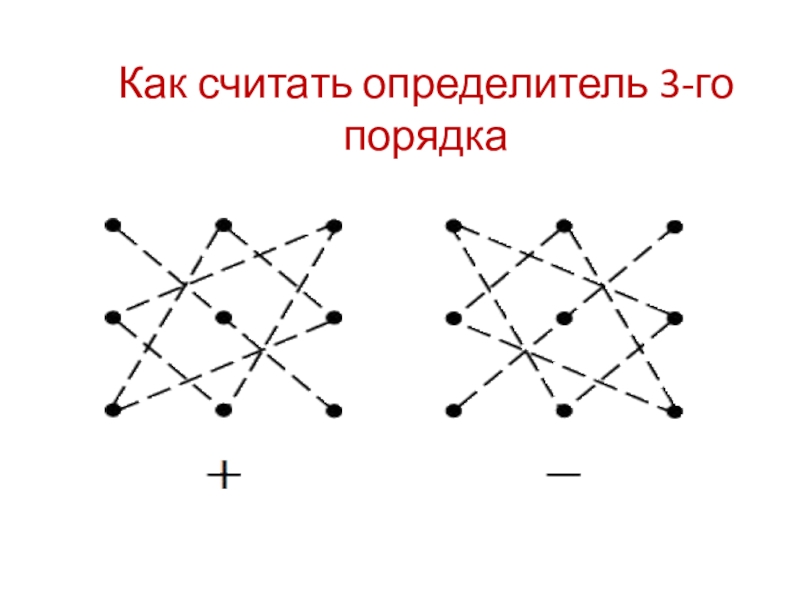
Слайд 6Что это за пентаграммы?
На первом рисунке мы берем три числа,
лежащие на диагонали, и перемножаем их. Затем берем другие тройки чисел, лежащие в вершинах треугольников, и тоже перемножаем их между собой. В результате всех этих действий мы получим три числа, которые надо сложить (поэтому внизу левой картинки стоит знак плюс).
Теперь разбираемся со второй картинкой. Здесь мы снова берем и перемножаем три числа, но уже на другой диагонали. Так же мы снова берем два треугольника и перемножаем числа, стоящие в их углах (отдельно для каждого треугольника). Полученные три числа опять складываем, а результат вычитаем из первого числа (поэтому внизу справа стоит знак минус).

Слайд 7Вычислить определитель
1 · 5 · 9 = 45
2 · 6 ·
7 = 84;
3 · 4 · 8 = 96.
45 + 84 + 96 = 225
3 · 5 · 7 = 105
2 · 4 · 9 = 72;
1 · 6 · 8 = 48;
105 + 72 + 48 = 225
=225 − 225 = 0.

Слайд 9Уравнение плоскости
Ax + By + Cz + D = 0
Плоскость задается тремя точками
А(х1;у1;z1) В(х2;у2;z2) С(х3;у3;z3)
Т(х; у;z)
точка с произвольными координатами. Принадлежащая этой плоскости

Слайд 10Проведем векторы и найдем их координаты

Слайд 11Составляем квадратную матрицу
Так как вектора лежат в одной плоскости, определитель равен
нулю.

Слайд 12Составить уравнение плоскости, проходящей через три точки
A1 = (0, 0, 1);
B1 = (1,

Слайд 13Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 ·
0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

Слайд 14Написать уравнение плоскости, проходящей через точки

Слайд 15 В единичном кубе составьте уравнение плоскости (А1EF), где Е –
середина В1С1,
1
1
1
F
E
A1 (1; 0; 1)
Е (0,5; 1; 1)
Запишем уравнение плоскости (А1EF):
Слайд 16В правильной четырехугольной пирамиде ребро основания равно 4, а высота –
6. Составьте уравнение плоскости (АDS).
Запишем уравнение плоскости (АSD):
(2;-2;0)
(-2;-2;0)
(0;0;6)