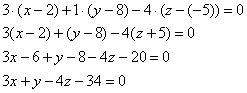Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости − теория, примеры и решения
Пусть задана точка M0(x0, y0, z0) и уравнение плоскости
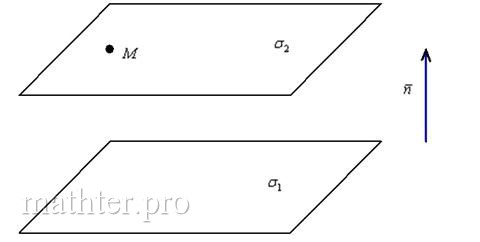
Наша задача найти уравнение плоскости, проходящей через точку M0 и параллельной плоскости (1)(Рис.1).
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (1):
Решим (2) относительно D:
Подставляя значение D из (3) в (1), получим:
Уравнение (4) можно представить также в следующем виде:
Уравнение (5) является уравнением плоскости, проходящей через точку M0(x0, y0, z0) и параллельной плоскости (1).
Пример 1.
Найти уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости :
Решение.
Запишем коэффициенты нормального вектора плоскости (6):
Подставляя координаты точки M0 и координаты нормального вектора в (3), получим:
Подставляя значения A, B, C, D в уравнение плоскости (1), получим:
Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:
Ответ.
Уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:
5.3.1. Как найти плоскость, параллельную данной?
Задача 137
Найти плоскость, проходящую через точку параллельно плоскости
.
Решение: Обозначим известную плоскость через . По условию требуется найти плоскость
, которая параллельна плоскости
и проходит через точку
. …Какие есть идеи? Немножко подумайте …
А ещё лучше выполнить схематический чертёж, который сразу поможет с идеей:
У параллельных плоскостей один и тот же вектор нормали. Добавить нечего =) Осталось оформить мат в два хода:
1) Из уравнения найдём нормальный вектор
.
2) Уравнение плоскости составим по точке
и вектору
:
Ответ:
Как выполнить проверку, я уже рассказал. Продолжаем раскидывать стог сена пространственной геометрии:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Пусть имеется точка М 0 (x
0, y 0, z
0) и два неколлинеарных вектора
и
.
Требуется найти уравнение плоскости,
проходящей через точку М 0
параллельно векторам
и
.
Возьмем произвольную точку М(x,
y, z),
принадлежащую искомой плоскости.
Тогда векторы
являются
компланарными и их смешанное произведение
равно нулю. Имеем уравнение:
.
Рассмотренный подход к получению
уравнения плоскости используется, в
частности, при выводе уравнения плоскости,
проходящей через три заданные точки.
Пусть имеются три точки М 1 (x
1, y 1, z
1), M 2 (x
2, y 2, z
2), M 3 (x
3, y 3,
z 3). Требуется
найти уравнение плоскости, проходящей
через эти точки. Возьмем на плоскости
произвольную точку М
(x, y,
z) и
рассмотрим векторы
=
(x 2 – x
1; y 2 –
y 1; z
2 – z 1),
=
(x 3 – x
1; y 3 –
y 1; z
3 – z 1)
и
=
(x – x
1; y –
y 1; z
– z 1),
которые лежат в искомой плоскости и,
следовательно, компланарны. Их смешанное
произведение равно нулю. Получим искомое
уравнение
.
3. Уравнение плоскости «в отрезках».
Уравнение плоскости вида
называется уравнением плоскости «в
отрезках». Его легко получить из
общего уравнения плоскости A
x + B
y + С
z + D
= 0 при условии, что все коэффициенты А,
В, С и D отличны
от нуля.
A x
+ B
y
+ С
z
+ D = 0
A
x
+ B
y
+ С
z
= –D
.
Обозначая знаменатели дробей в последнем
уравнении через a ,
b и c,
получим уравнение
.
В этом уравнении числа a,
b и с равны
величинам отрезков, которые плоскость
отсекает на осях координат. Действительно,
при х = y = 0 получим
z = c,
при x = z
= 0 получим y = b,
а при y = z
= 0 получим x = a,
то есть точки (0, 0, c),
(0, b, 0) и (a,
0, 0) являются точками пересечения
плоскости с осями OX,
OY и OZ
соответственно.
4. Угол между плоскостями.
Углом между плоскостями называется
острый угол между
ними.
16
Пусть плоскости P1
и P2 заданы
уравнениями:
P1: A
1 x + B
1 y + C
1 z + D
1 = 0,
— вектор нормали,
P2: A
2 x + B
2 y + C
2 z + D
2 = 0,
,
— вектор нормали.
Заметим, что угол между векторами
нормалей равен либо углу ,
либо смежному с ним тупому углу ,
так как эти векторы направлены
перпендикулярно плоскостям. В результате
получаем cos
= cos
()
=
=
=
=
.
§ 5. Прямая в пространстве
1. Канонические уравнения прямой.
Вывод канонических уравнений прямой
производится точно так же, как это
делалось для прямой на плоскости.
Пусть даны точка М 0 (x
0, y 0, z
0) и вектор
—
направляющий вектор прямой. Требуется
найти уравнение прямой, проходящей
через точку М 0 параллельно
вектору
.
Возьмем на искомой прямой произвольную
точку М (x, y,
z) и рассмотрим
и
— радиусы-векторы точек М и М
0. Вектор
лежит на прямой и, следовательно,
коллинеарен вектору
,
что равносильно векторному равенству
–
=
t
— векторному параметрическому
уравнению прямой. Переписав это
уравнение в координатной форме, получим
параметрические уравнения прямой
.
Из параметрических уравнений получаем
канонические уравнения прямой в
пространстве
=
=
,
которые представляют собой условия
пропорциональности координат коллинеарных
векторов
и
.
Уравнения прямой, проходящей через
две заданные точки M
1 (x 1, y
1, z 1) и M
2 (x 2, y
2, z 2), имеют
вид
=
=
,
так как вектор
17
=
,
лежащий на прямой, можно использовать
в качестве направляющего вектора.
Прямые, заданные каноническими или
параметрическими уравнениями будут
параллельны, если их направляющие
векторы коллинеарны, и перпендикулярны,
если их направляющие векторы ортогональны:
Пусть прямые L 1
и L 2,
заданы каноническими уравнениями:
L1:
=
=
,
— направляющий вектор,
L2:
=
=
,
— направляющий вектор.
Тогда условия параллельности и
перпендикулярности этих прямых
описываются следующим образом:
L 1
L 2
;
L 1
L
2
.
Угол между прямыми
L 1 и
L 2
вычисляется по формуле
cos
=
=
=
,
так как угол между направляющими
векторами
и
данных
прямых равен либо углу ,
либо смежному с ним углу
– .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение плоскости, проходящей через заданную точку параллельно заданной плоскости.
В этой статье детально разобран процесс нахождения уравнения плоскости, проходящей через заданную точку трехмерного пространства параллельно заданной плоскости. После изложения необходимых теоретических основ приведены подробные решения характерных задач, в которых находится уравнение плоскости, проходящей через заданную точку пространства параллельно заданной плоскости.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через заданную точку пространства параллельно заданной плоскости.
Задача нахождения уравнения плоскости, проходящей через заданную точку пространства параллельно заданной плоскости, возникает из следующей теоремы: через любую точку пространства, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной. Доказательство этой теоремы можно найти в учебнике геометрии для 10 — 1 1 классов, указанном в конце статьи.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней задана плоскость и точка , не лежащая в плоскости . Поставим перед собой задачу: написать уравнение плоскости , проходящей через точку параллельно плоскости .
Нам известно, что общее уравнение плоскости, проходящей через точку и имеющей нормальный вектор плоскости , имеет вид . Таким образом, мы сможем записать требуемое уравнение плоскости , если определим координаты ее нормального вектора.
При изучении темы «нормальный вектор плоскости» мы отметили, что нормальный вектор одной из двух параллельных плоскостей является нормальным вектором второй плоскости. Следовательно, в силу параллельности плоскостей и , нормальным вектором плоскости является любой нормальный вектор заданной плоскости . Таким образом, задача составления уравнения плоскости , проходящей через заданную точку М1 параллельно заданной плоскости , сводится к определению координат нормального вектора плоскости . В свою очередь координаты нормального вектора плоскости проще всего получить, если иметь перед глазами общее уравнение плоскости вида . В этом случае коэффициенты A , B , C перед переменными x , y , z являются соответствующими координатами нормального вектора плоскости .
Итак, запишем алгоритм нахождения уравнения плоскости , проходящей через заданную точку параллельно заданной плоскости :
- получаем общее уравнение плоскости в виде (если оно нам уже не дано в условии) и записываем ее нормальный вектор ;
- принимаем этот вектор в качестве нормального вектора плоскости ;
- записываем уравнение плоскости, проходящей через точку и имеющей нормальный вектор , в виде — это и есть искомое уравнение плоскости , проходящей через заданную точку параллельно заданной плоскости.
Следует заметить, что если точка М1 лежит в плоскости , то, действуя по записанному алгоритму, мы получим уравнение плоскости , которая совпадает с плоскостью .
Примеры составления уравнения плоскости, проходящей через заданную точку параллельно заданной плоскости.
Разберем решения нескольких примеров, в которых требуется составить уравнение плоскости, проходящей через заданную точку пространства параллельно заданной плоскости.
Начнем с самого простого случая, когда координаты нормального вектора плоскости очень легко находятся.
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости − теория, примеры и решения
Наша задача найти уравнение плоскости, проходящей через точку M0 и параллельной плоскости (1)(Рис.1).
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (1):
Решим (2) относительно D:
Подставляя значение D из (3) в (1), получим:
| Ax+By+Cz−(Ax0+By0+Cz0)=0 | (4) |
Уравнение (4) можно представить также в следующем виде:
| A(x−x0)+B(y−y0)+C(z−z0)=0 | (5) |
Уравнение (5) является уравнением плоскости, проходящей через точку M0(x0, y0, z0) и параллельной плоскости (1).
Найти уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости :
Запишем коэффициенты нормального вектора плоскости (6):
Подставляя координаты точки M0 и координаты нормального вектора в (3), получим:
Подставляя значения A, B, C, D в уравнение плоскости (1), получим:
Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:
Уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:
Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )
Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.
Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.
Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0
Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.
Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:
2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0
Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:
λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0
Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0
- Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:
M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0
Ответ: 3 x + 7 y — 5 z — 26 = 0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
- Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.
- При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0
Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0
Ответ: x — 7 = 0
Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .
Решение
Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .
Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .
http://matworld.ru/analytic-geometry/uravnenie-ploskosti2-online.php
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-ploskosti/