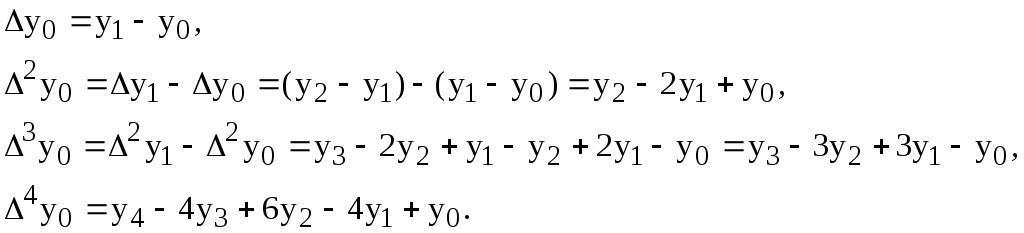Как найти уравнение полинома по точкам

Интерполяционный многочлен Лагранжа (полином Лагранжа)

Этот онлайн калькулятор строит интерполяционный многочлен Лагранжа для заданного набора точек. Калькулятор также строит график, на который выводит как полином Лагранжа, так и базисные полиномы, интерполирует заданные точки и показывает пошаговое решение.

Этот калькулятор может пригодиться при решении задач на интерполяцию полиномом Лагранжа. В таких задачах обычно требуется интерполировать значение неизвестной функции, соответствующее некоторому значению x, использую формулу интерполяционного многочлена Лагранжа, полученную из известного набора точек со значениями неизвестной функции (x, f(x)).

Калькулятор ниже обладает следующими функциями:

1. Он находит формулу полинома Лагранжа для заданного набора точек.
2. Он отображает пошаговый вывод формулы.
3. Он вычисляет значения интерполяционного многочлена Лагранжа для заданных точек (интерполирует функцию полиномом Лагранжа в заданных точках интерполяции)
4. Он отображает набор точек, значения в точках интерполяции, полином Лагранжа и все базисные полиномы на графике.

Как пользоваться

Сначала вводите набор точек — одна точка на строку в форме x f(x), значения разделены пробелом. Если вы хотите получить интерполяцию, вводите значения точек интерполяции в следующее поле в виде значений x, разделенных пробелом.

По умолчанию, калькулятор отображает формулу многочлена и его значения в точках интерполяции. Если нужно пошаговое решение, включите опцию «Показать пошаговое решение». Также можно отключить отображение базисных полиномов.

Теория и формулы, как обычно, описаны под калькулятором.

Подбор полинома по заданным точкам

По заданным точкам построен полином

Это является одним из видов аппроксимации, но практически, редко используется. Связанно это с тем, что несмотря на то что в узловых точках (исходных) значение вычсленного полинома совпадает на 100%, в промежуточных точках значение может быть очень далеким от реальных значений.

Простой пример это показывает. Пусть какому то ученому пришла в голову рассчитать аппроксимирующий полином, который показывал бы как растет человек год от года.

Он запросил данные и получил, что в первый год рост человека 50см, на 3 год — 80 см, в 6 лет -120см, в 15 лет -150 см, а в 25 лет — 180 см

Введя данные он получил следующий полином

По заданным точкам построен полином

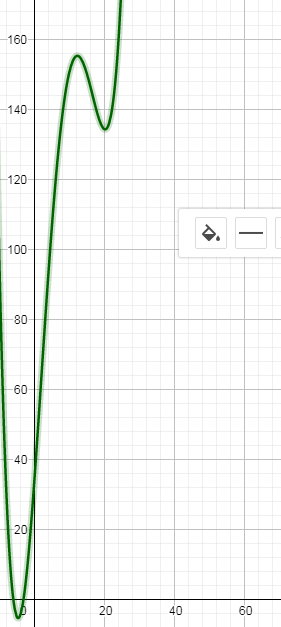
Вроде бы все хорошо, в каждой контрольной точке, значения совпадают, но если мы посмотрим график.

Удивительно, но где то в 20 лет у человека рост резко уменьшается до 130 см.

Мы то с Вами прекрасно понимаем, что это не так, но в других расчетах, такая аппроксимация может приводить вот к таким «аномалиям» и следовательно к неверным выводам.

Для чего же тогда нужен этот калькулятор?

Если мы знаем(!) что наша неизвестная функция есть многочлен какой то степени, то взяв необходимое количество точек, мы всегда с высокой точностью определим эти коэффициенты.

Я хочу определить какой многочлен поможет найти зависимость, от следующих значений, если при

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Полином одной переменной

Полиномы нескольких переменных рассматриваются ☞ ЗДЕСЬ.

Будем обозначать через $ mathbb A_<> $ какое-либо из множеств $ mathbb Z,mathbb Q, mathbb R_<> $ или $ mathbb C_<> $.

Общая информация

Функция вида $$ f(x)=a_0x^n+a_1x^+dots+a_n = sum_^n a_jx^ $$ при $ n_<> in <0,1,dots >$ и $ ,dots,a_n>subset mathbb A $ относительно переменной $ x_<> $ называется полиномом 1) или многочленом от указанной переменной над множеством $ mathbb A_<> $. Число $ a_ $ называется коэффициентом 2) полинома (при $ (n-j)_<> $-й степени переменной), выражение $ a_x^ $ — членом (одночленом) полинома, $ a_ $ — свободным членом, $ x_<>^ $ — мономом.

Пример. Выражения

$$ x^<2>+2,x-679, x^<2>+sqrt<2>x-pi , <mathbf i>, x^<3>- 2,x +sqrt <3>$$ являются полиномами; а $$ x^<-2>+3, x +x^ <2>, x^, sum_^ <infty>x^/j_<> $$ полиномами не являются.

Если $ a_<0>ne 0 $, то член $ a_0x^ $ называется ведущим членом, а $ a_ <0>$ — старшим коэффициентом полинома. При этом число $ n_<> $ называется степенью полинома и обозначается 3) $ deg f_<>(x) $. Полином первой степени называется линейным полиномом. Полином, все коэффициенты которого, кроме, возможно, $ a_ $, равны нулю, называется константой 4) ; будем обозначать его const. Очевидно, что степень константы равна нулю; исключительным для этого утверждения является случай когда константа является нулем. Если все коэффициенты полинома равны нулю, то такой полином называется (тождественно) нулевым. В этом случае его степень не определяется.

На переменную $ x_<> $ мы пока не накладываем ни какого ограничения: она может принимать значения из любого указанного выше множества — не обязательно из того, которому принадлежат коэффициенты полинома. Обозначим область определения полинома через $ mathbb B_<> $.

Значением полинома при (или в точке) $ cin mathbb B_<> $ называется число $$ f(c) = a_0c^n+a_1c^+dots+a_n . $$

Два полинома $$ f(x)=a_0x^n+dots+a_n u g(x)=b_0x^m+dots+b_m $$ с коэффициентами из $ mathbb A $ называются (тождественно) равными: $$ f(x)equiv g(x) $$ если совпадают множества их членов; или, что то же, равны их степени и равны коэффициенты при одинаковых степенях переменной.

Это определение отличается от привычного определения равенства двух функций: две функции $ F_<>(x) $ и $ G(x)_<> $ называются равными на множестве $ mathbb B_<> $ если совпадают их значения при любом $ x in mathbb B_<> $. На самом деле, для случая полиномов эти два определения — алгебраическое и функциональное — эквивалентны.

Теорема. $ f_<>(x)equiv g(x) $ тогда и только тогда, когда $ f(c)=g(c)_<> $ для $ forall cin mathbb B_<> $.

Одним из следствий теоремы является тот факт, что для полинома совершенно не важен порядок следования его членов; в частности, наряду с записью полинома по убывающим степеням переменной, мы имеем право записывать его и по возрастающим: $ f_<>(x)= sum_^n a_x^ $. Форма полинома, в которой его разложение записывается по убывающим степеням переменной, называется его канонической формой. Кроме того, теорема дает нам право на операцию, называемую приведением подобных членов: $$ ax^+bx^j equiv (a+b)x^j, quad ax^jcdot bx^k=ab x^ .$$ Имея в виду этот факт, определим теперь две основные операции для полиномов: сложение и умножение.

Суммой двух полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином, составленный как сумма всех одночленов, входящих в состав $ f_<>(x) $ и $ g_<>(x) $: $$ f(x) + g(x) = (a_n+b_m) + (a_+b_)x+dots + left<begin (a_0+b_0)x^n & npu m=n, \ a_0x^n & npu m n. end right. $$

Теорема. $ deg (f+g_<>)le max (deg f, deg g) $.

Произведением двух полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином, составленный как сумма всевозможных попарных произведений членов первого полинома на члены второго: $$ begin f(x)g(x) &=& a_0b_0x^+(a_1b_0+a_0b_1)x^ +(a_2b_0+a_1b_1+a_0b_2)x^+ \ & &+dots + (a_0b_k+a_1b_+dots+a_kb_0)x^+ dots + a_nb_m . end $$ (В записи коэффициента при $ x^ $ мы полагаем $ a_= 0 $ при $ j>n_<> $ и $ b_ <ell>= 0 $ при $ ell>m_<> $).

Теорема. Если $ f_<>(x) notequiv 0 $ и $ g_<>(x) notequiv 0 $, то $ deg (fcdot g_<>)= deg f + deg g_<> $.

Фактическое выполнение операции перемножения полиномов возможно по схеме, напоминающей алгоритм умножения целых чисел «столбиком»: это позволяет сэкономить время на выписывание степеней переменной.

Пример. Перемножить полиномы

Решение. Представим полиномы наборами их коэффициентов, расположив один из них горизонтально, а второй — вертикально. Умножение полинома $ f_<>(x) $ на $ b_x^ $ сводится к умножению набора $ (a_<0>,dots,a_n) $ на $ b_ $; результат следующего умножения — на $ b_x^ $ — получается аналогичным образом, но записывается со сдвигом на одну позицию вправо. Получившиеся ряды суммируются по столбцам. $$ begin &1 & 0 & 1 & -2& 0 & 3 \ hline 2 & 2 & 0 & 2 & -4 & 0 & 6 \ -3& & -3 & 0 & -3 & 6 & 0 & -9 \ 4 & & & 4 & 0 & 4 & -8 & 0 & 12 \ 0 & & & \ -1 &&&&& -1 & 0 & -1 & 2 & 0 & -3 \ hline& 2 & -3 & 6 & -7 & 9 & -2 & -10 & 14 & 0 & -3 end $$ (В отличие от перемножения чисел здесь результаты сложения в столбиках не переносятся в следующий разряд.)

Ответ. $ 2,x^<9>-3,x^8+6,x^7-7,x^6+9,x^5-2,x^4-10,x^3+14,x^2 — 3 $.

Множество всех полиномов от переменной $ x_<> $ с коэффициентами из $ mathbb A_<> $ будем обозначать $ mathbb A_<> [x] $.

Способы более эффективного умножения полиномов излагаются ☞ ЗДЕСЬ

Схема Хорнера

Задача. Вычислить значение полинома в точке $ c $.

Схема вычисления, заложенная в самом определении, «стóит» $ 3n_<>-1 $ операции: $$ begin & &c^2=ctimes c, & dots, & c^n=c^times c , \ &a_ times c, & a_ times c^2, & dots, & a_0 times c^n ,\ a_n & +a_ times c & + a_ times c^2 & + dots & + a_0 times c^n, end $$ т.е. $ 2n_<>-1 $ операции умножения и $ n_<> $ операций сложения. Организуем теперь вычисления по-другому: $$ begin f(c)&=&a_n+a_c+a_c^2+dots +a_1c^+a_0c^n = \ &=&a_n+cleft(a_+a_c+ dots + a_0c^ right) = \ &= &a_n+cleft(a_+cleft(a_+dots + a_0c^ right) right) = \ &=& dots = \ &=&a_n+cleft(a_+cleft(a_+dots + c(a_1+ a_0c)dots right) right) . end $$ Начинаем вычислять с самой внутренней скобки: $$<mathfrak b>_1= a_1+ a_0c, <mathfrak b>_2= a_2+ <mathfrak b>_1 c,dots, <mathfrak b>_ = a_ +<mathfrak b>_c,, <mathfrak b>_ = a_ +<mathfrak b>_c=f(c) $$ Вычисление каждой величины $ <mathfrak b>_ $ «стоит» $ 2_<> $ операции — одного сложения и одного умножения (при условии, что предварительно вычислено $ <mathfrak b>_^<> $). Приведем компактную запись алгоритма: $$ <mathfrak b>_k = a_k + <mathfrak b>_c quad npu quad <mathfrak b>_0 = a_0 quad u quad kin <1,dots,n > . $$ «Стоимость» вычисления значения $ f_<>(c) $ по этой схеме Хорнера составляет $ 2n_<> $ операций. Налицо экономия по сравнению с прямым способом вычисления $ f_<>(c) $.

Вычисления удобно производить с помощью таблицы, стартовое состояние которой следующее: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 end $$ Будем отсчитывать строки сверху вниз, начиная от горизонтальной черты, т.е. нулевой строкой будем считать строку из коэффициентов полинома. Вычисление значения $ <mathfrak b>_ <1>$ в первой строке производится по схеме: предыдущее число умножается на $ c_<> $ и складывается с верхним, т.е. $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 & underbrace_<<mathfrak b>_1> end $$ Далее вычисления идут по тому же правилу: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 &<mathfrak b>_1&underbrace_1>_<<mathfrak b>_2> end $$ и т.д. Величина, получившаяся в последнем столбце, и будет искомым значением $ f_<>(c) $: $$ begin & a_0 & a_1 & a_2 & dots & a_ & a_ & a_n \ hline c & a_0 &<mathfrak b>_1&<mathfrak b>_2&dots &<mathfrak b>_ & <mathfrak b>_& underbrace_>_<<mathfrak b>_n=f(c)> end $$

Пример. Вычислить значение полинома $ x^<5>-3, x +1 $ в точке $ 2+ mathbf i_<> $.

Решение. $$ begin & 1 & 0 & 0 & 0 & -3 & 1 \ hline 2+ mathbf i & 1& 2+mathbf i &3+4 mathbf i &2+11 mathbf i & -10+24mathbf i& -43+38mathbf i end $$

Ответ. $ -43+38mathbf i_<> $.

Выясним теперь смысл коэффициентов $ <mathfrak b>_<1>,dots, <mathfrak b>_ $ первой строки схемы Хорнера.

Теорема. Пусть $ cin mathbb B_<> $ и $ mathbb Bsubset mathbb A_<> $. Полином $ f_<>(x)in mathbb A[x] $ допускает единственное представление в виде:

$$ f(x)equiv (x-c)q(x)+r npu r=constin mathbb A, q(x)in mathbb A[x], deg q = deg f — 1 . $$

Доказательство. Будем искать константу $ r_<> $ и полином $ q_<>(x) $ методом неопределенных коэффициентов: $ q(x)= q_<0>x^+q_1x^+ dots + q_ $. Подставим его в правую часть доказываемого тождества, приведем подобные и приравняем коэффициенты полученного полинома коэффициентам полинома $ f_<>(x) $. Получим линейные уравнения, из которых последовательно определяем $ q_<0>,q_1, dots, q_ $ : $$ begin x^n& a_0&=q_0, & \ x^& a_1&=q_1-q_0c &Rightarrow q_1=a_1+q_0c, \ x^& a_2&=q_2-q_1c &Rightarrow q_2=a_2+q_1c, \ vdots & & dots & \ x & a_&=q_-q_c &Rightarrow q_=a_+q_c,\ 1 & a_n&=qquad -q_c+r & Rightarrow r=a_n+q_c. end $$ Видим, что формулы, определяющие коэффициенты $ q_ $, полностью совпадают с формулами, определяющими элементы первой строки схемы Хорнера, т.е. $ q_0=<mathfrak b>_<0>,dots,q_=<mathfrak b>_ $. Но тогда $ r=a_n+q_c=a_+<mathfrak b>_c=<mathfrak b>_=f(c) $. ♦

Итак, имеем: $$q(x)=<mathfrak b>_0x^+dots+<mathfrak b>_, r=<mathfrak b>_ , $$ при этом все коэффициенты вычисляются по схеме Хорнера, а старший коэффициент полинома $ q_<>(x) $ совпадает со старшим коэффициентом $ f_<>(x) $. Так, для полинома приведенного выше примера имеет место тождество: $$x^5-3, x +1 equiv $$ $$ equiv (x-2-mathbf i)left(x^4+ (2+mathbf i)x^3+(3+4,mathbf i)x^2+ (2+11,mathbf i)x -10+24,mathbf i right) -43+38 mathbf i . $$

Корни

Если значение полинома $ f_<>(x) $ при $ x=cin mathbb B_<> $ равно нулю, то число $ c_<> $ называется корнем полинома $ f_<>(x) $. Иными словами, корень полинома $ f_<>(x) $ — это решение уравнения $ f_<>(x)=0 $, принадлежащее множеству $ mathbb B_<> $.

Уравнение $ f_<>=0 $, в левой части которого стоит полином одной или нескольких переменных, называется алгебраическим.

Задача. Выяснить количество корней полинома $ f_<>(x)in mathbb A[x] $, принадлежащих множеству $ mathbb B_<> $, и вычислить их.

Решить алгебраическое уравнение $ f_<>(x)=0 $ над множеством $ mathbb B $ означает найти все корни $ f_<>(x) $, принадлежащие $ mathbb B_<> $.

На основании теоремы из предыдущего пункта имеет место следующая

Теорема [Безу]. Пусть $ mathbb B subset mathbb A_<> $ и $ cin mathbb B_<> $ — корень полинома $ f_<>(x), deg fge 1 $. Тогда полином $ f_<>(x)in mathbb A [x] $ допускает представление в виде произведения:

$$ f(x)equiv (x-c)f_1(x) , $$ где полином $ f_<1>(x)in mathbb A [x], deg f_1 = deg f — 1 $ определяется единственным образом.

Итак, теорема Безу утверждает, что в случае существования корня полинома, возможно разложение этого полинома в произведение двух полиномов — одного первой степени и одного полинома степени, на единицу меньшей исходного. Тем самым, задача о нахождении корней полинома $ f_<>(x) $ сведется к аналогичной задаче для полинома $ f_<1>(x) $; вторая задача может оказаться более простой за счет понижения степени.

Фактическое нахождение полинома $ f_<1>(x) $ возможно произвести с помощью схемы Хорнера.

Пример. Решить уравнение

$$ x^<3>+3 mathbf i, x^2-3(1+2 mathbf i)x+10-5 mathbf i =0 $$ над множеством $ mathbb C_<> $, если известно, что число $ (-1-2 mathbf i)_<> $ — одно из его решений.

Решение. Строим схему Хорнера: $$ begin & 1& 3mathbf i & -3(1+2 mathbf i) & 10-5 mathbf i \ hline -1-2 mathbf i & 1& -1+ mathbf i & -5 mathbf i & 0 end $$ Видим, что число $ (-1-2 mathbf i)_<> $ действительно является корнем полинома, и, следовательно, последний раскладывается в произведение двух полиномов: линейного и квадратичного. Коэффициенты квадратичного полинома выбираются из той же схемы: $$ (x+1+2 mathbf i )(x^2 + (-1+ mathbf i )x- 5 mathbf i) . $$ Квадратное уравнение над $ mathbb C_<> $ можно решить (см. ☞ ЗДЕСЬ ), его корни: $ (-1-2 mathbf i)_<> $ и $ 2+mathbf i_<> $.

Ответ. $ (-1-2 mathbf i), 2+ mathbf i_<> $.

Если полином $ f_<>(x) $ раскладывается в произведение $ f_<>(x)equiv (x-c)f_1(x) $, то полином $ (x-c) $ называется линейным множителем для $ f_<>(x) $ над множеством $ mathbb B_<> $.

Для того, чтобы $ (x-c)_<> $ был линейным множителем для $ f_<>(x) $ необходимо и достаточно чтобы число $ c_<> $ было корнем $ f_<>(x) $.

Примеры показывают, что не для всякого полинома и множества $ mathbb B_<> $ корни существуют. Очевидно не имеет корней полином нулевой степени (константа, отличная от нуля); любой полином первой степени над $ mathbb A_<> $ имеет единственный корень, принадлежащий $ mathbb A_<> $. Квадратный полином $ x^<2>+1 $ не имеет вещественных корней, но имеет мнимые.

Основная теорема высшей алгебры

Теорема. Любой полином с комплексными коэффициентами, степень которого больше нуля, имеет хотя бы один корень, в общем случае, комплексный.

Эта теорема гарантирует существование корня $ lambda_<1>in mathbb C $. На основании теоремы Безу, можно утверждать, что $ f_<>(x) $ допускает представление $$ f(x)equiv (x-lambda_1)f_1(x) quad npu quad f_1(x)in mathbb C [x], deg f_1(x)=deg f(x) -1 .$$ Если $ deg f_<1>(x) ge 1 $, то, по той же теореме, полином $ f_<1>(x) $ также должен обладать корнем, который мы обозначим 5) $ lambda_ <2>$; теорема Безу гарантирует тогда представление $$ f(x)equiv (x-lambda_1)(x-lambda_2)f_2(x) quad npu quad f_2(x)in mathbb C [x], deg f_2(x)=deg f(x) -2 .$$ Продолжая процесс далее, мы за $ n_<> $ шагов придем к представлению $$ f(x)equiv (x-lambda_1)(x-lambda_2)times dots times (x-lambda_n)f_n(x) quad npu quad f_n(x)in mathbb C[x], deg f_n(x)=0 ,$$ т.е. полином $ f_(x)^<> $ представляет собой константу. На основании условия тождественного равенства полиномов утверждаем, что $ f_(x) equiv a_0 $. Таким образом приходим к следующей альтернативной версии основной теоремы высшей алгебры.

Теорема. Для произвольного полинома $ f_<>(x) $ степени $ n_<>ge 1 $ существует его представление в виде произведения линейных множителей

$$ f(x)equiv a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_n) ; $$ это представление единственно с точностью до перестановки сомножителей.

Как уже отмечалось в доказательстве теоремы, в этом представлении могут встречаться одинаковые линейные сомножители. Собрав их вместе, получим иной вид этого представления $$ f(x)equiv a_0(x-lambda_1)^<<mathfrak m>_<1>>times dots times (x-lambda_<mathfrak r>)^<<mathfrak m>_<<mathfrak r>>> , npu <mathfrak m>_<1>+<mathfrak m>_<2>+dots+<mathfrak m>_<mathfrak r>=n $$ и все числа $ lambda_<1>,dots,lambda_ <mathfrak r>$ теперь различны. Эта формула называется формулой разложения полинома $ f_<>(x) $ на линейные сомножители или линейным представлением полинома $ f_<>(x) $; при этом число $ <mathfrak m>_^<>in mathbb N $ называется кратностью линейного сомножителя $ x-lambda_ $ или кратностью корня $ lambda_ $ в полиноме $ f_<>(x) $. Корень $ lambda_ $ называется простым, если $ <mathfrak m>_=1_<> $ и кратным кратности $ <mathfrak m>_^<> $ если $ <mathfrak m>_>1_<> $ (двойным или двукратным, если $ <mathfrak m>_=2_<> $, тройным или трехкратным если $ <mathfrak m>_=3_<> $ и т.д.)

Пример. Найти линейное представление полинома $ f(x)=x^<6>-2, x^3+1 $.

Решение. Линейное представление легко получить если сначала заметить, что $ f(x)equiv (x^3-1)^ <2>$, а затем использовать выражения для корней кубических из единицы: $$f(x)equiv (x-1)^2 left(x- frac<-1+ mathbf i sqrt<3>> <2>right)^2 left(x- frac<-1 — mathbf i sqrt<3>> <2>right)^2 . $$ Все корни полинома имеют вторую кратность. ♦

Выведение условия наличия кратного корня (в терминах коэффициентов полинома) ☞ ЗДЕСЬ. При известном корне, нахождение его кратности ☞ ЗДЕСЬ.

Теорема. Два полинома, степени которых не превосходят $ n_<> $, равны тождественно если они имеют равные значения более чем при $ n_<> $ различных значениях переменной.

Доказательство необходимости очевидно. Если полиномы $ f_<>(x) $ и $ g_<>(x) $ удовлетворяют условию теоремы, то полином $ f(x)-g_<>(x) $ должен иметь более, чем $ n_<> $ корней, что, ввиду основной теоремы высшей алгебры, возможно лишь если он тождественно нулевой. ♦

Теорема утверждает, что полином $ f_<>(x) $ степени, $ le n_<> $, однозначно определяется своими значениями при более чем $ n_<> $ различных значениях переменной. Можно ли эти значения задавать произвольно? Оказывается задание $ (n+1)_<> $-й пары $ (x_<1>,y_1),dots,(x_,y_) $ при всех различных $ x_<1>,dots,x_ $ позволяет однозначно определить полином $ f_<>(x) $ такой, что $ f(x_<1>)=y_1,dots,f(x_)=y_ $ и $ deg f_<> le n $. Практические способы решения этой задачи обсуждаются в разделе ☟

Интерполяция

Корни и коэффициенты полинома

Симметрические функции корней

Разложение полинома $ f_<>(x) $ на линейные множители дает интересные соотношения между корнями полинома и его коэффициентами. Сначала выведем их для малых степеней. Для $ n_<>=2 $: $$a_0x^2+a_1x+a_2equiv a_0(x-lambda_1)(x-lambda_2)equiv a_0x^2-a_0(lambda_1+lambda_2)x+a_0lambda_1lambda_2 Rightarrow $$ $$ Rightarrow left< begin lambda_1+lambda_2&=&-a_1/a_0, \ lambda_1lambda_2&=&a_2/a_0, end right. $$ т.е. получили формулы известные из школьного курса алгебры. Далее, для $ n_<>=3 $: $$a_0x^3+a_1x^2+a_2x+a_3equiv a_0(x-lambda_1)(x-lambda_2)(x-lambda_3)equiv $$ $$equiv a_0x^3-a_0(lambda_1+lambda_2+lambda_3)x^2+a_0(lambda_1lambda_2 + lambda_1lambda_3+lambda_2lambda_3)x-a_0lambda_1lambda_2lambda_3 Rightarrow $$ $$ Rightarrow left< begin lambda_1+lambda_2+lambda_3&=&-a_1/a_0, \ lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3&=&a_2/a_0,\ lambda_1lambda_2lambda_3&=&-a_3/a_0. end right. $$

Теорема. Для корней $ lambda_<1>,dots,lambda_n $ полинома

$$ f(x)=a_<0>x^n+a_1x^+dots+a_n,, a_0ne 0 $$ справедливы формулы Виета $$ sum_ <1 le jle n>lambda_j = lambda_1+ dots+ lambda_n= -frac, $$ $$ sum_<1le j_1 ☞ ЗДЕСЬ.

Биографические заметки о Виете ☞ ЗДЕСЬ

Пример. Найти все корни полинома $ 3,x^3-16,x^2+23,x-6 $, если известно, что произведение двух из них равно $ 1_<> $.

Решение. Имеем: $$ left< begin lambda_1+lambda_2+lambda_3&=&16/3, \ lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3 &=&23/3,\ lambda_1lambda_2lambda_3&=&6/3=2. end right. $$ Вдобавок к этим уравнениям, мы должны записать дополнительное условие: $$lambda_1 lambda_2=1 .$$ Из третьего уравнения системы получаем тогда $ lambda_3=2 $. Подставив его в два оставшихся, придем к двум идентичным: $$lambda_1 + lambda_2=10/3 .$$ Теперь для нахождения неизвестных $ lambda_ <1>$ и $ lambda_ <2>$ можем воспользоваться формулами Виета «в обратном порядке», составив квадратный полином, имеющий их корнями: $$t^2-10/3,t+1 .$$

Ответ. $ 2,,3,, 1/3 $.

Можно ли использовать формулы Виета для решения уравнения ?

Ответ ☞ ЗДЕСЬ.

Обдумаем еще раз результаты основной теоремы высшей алгебры и формул Виета. С одной стороны, задав коэффициенты $ a_<0>,a_1,dots,a_n $ мы однозначно определяем набор из $ n_<> $ комплексных чисел $ lambda_<1>,dots,lambda_n $ — корней этого полинома. С другой стороны, задав произвольным образом набор корней $ lambda_<1>,dots,lambda_n $, по формулам Виета однозначно определим величины $ a_1/a_0,dots,a_n/a_0 $. Для простоты, рассмотрим подмножество полиномов степени $ n_<> $, имеющих старший коэффициент равным $ 1_<> $. Получаем тогда взаимно-однозначное соответствие: $$ (a_1,dots,a_n) leftrightarrow (lambda_1,dots,lambda_n) . $$ Итак, каждый корень $ lambda_ $ полинома является какой-то функцией его коэффициентов $ a_1,dots,a_ $, т.е. формально говоря, функцией от многих переменных. Относительно этой функции мы пока ничего сказать не можем; более того, как мы узнаем НИЖЕ, для степеней полинома бóльших $ 4_<> $ не существует «хороших» общих формул, выражающих корни полинома через его коэффициенты. Несмотря на это, формулы Виета подтверждают, что некоторые комбинации этих неизвестных нам функций оказываются равными коэффициентам полинома. Какова основная отличительная особенность этих комбинаций?

Функция $ Phi(x_1,dots,x_n) $ называется симметрической функцией своих переменных, если ее значение не меняется ни при какой перестановке этих переменных: $$Phi(x_1,dots,x_n) equiv Phi(x_,dots,x_) $$ при всех различных $ j_1,dots, j_n in <1,dots,n>$.

Пример. Функции

$$ sqrt <1+x_1x_2x_3>, frac+frac+frac $$ являются симметрическими функциями переменных $ x_1,x_2,x_3 $, а функция $$ x_1^2x_2x_3+x_1x_2^2x_3 $$ симметрической функцией не является, поскольку ее значения меняются при перестанове $ (x_1,x_2,x_3) leftrightarrow (x_3,x_2,x_1) $.

В левых частях формул Виета как раз и стоят симметрические полиномы относительно $ lambda_<1>,dots,lambda_n $. Оказывается результат теоремы допускает следующее обобщение.

Теорема [Гаусс]. Значение любого симметрического полинома $ Phi(x_1,dots,x_n) $ на корнях $ lambda_1,dots,lambda_n $ полинома $ x^n+a_1x^+ dots+a_n $ является полиномиальной функцией от $ a_<1>,dots,a_n $: $$ Phi(lambda_1,dots,lambda_n) equiv <mathfrak F>(a_1,dots,a_n) . $$

Пример. Пусть $ lambda_ <1>$ и $ lambda_ <2>$ означают корни полинома $ x^2+a_1x+a_2 $. Выразить

$$lambda_1^2+lambda_2^2-3,lambda_1^2lambda_2-3,lambda_1lambda_2^2$$ через коэффициенты полинома.

Решение. Поскольку выражения для корней квадратного уравнения нам известны: $$ lambda_1= frac<-a_1+sqrt> <2>quad u quad lambda_2= frac<-a_1-sqrt> <2> , $$ то непосредственной подстановкой их в заданный полином, получаем $$ a_1^2-2,a_2+3,a_1a_2 . $$ ♦

Пример. Пусть $ lambda_1,, lambda_2,, lambda_3 $ означают корни полинома $ x^3+a_1x^2+a_2x+a_3 $. Выразить

$$lambda_1^2lambda_2+lambda_1^2lambda_3+lambda_1lambda_2^2+ lambda_1lambda_3^2+lambda_2^2lambda_3+lambda_2lambda_3^2 -lambda_1^2-lambda_2^2-lambda_3^2 $$ через коэффициенты полинома.

Решение. Выделим в требуемом выражении комбинации корней, стоящие в левых частях формул Виета. Первые $ 6_<> $ слагаемых можно представить в виде $$(lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3) (lambda_1+lambda_2+lambda_3)-3lambda_1lambda_2lambda_3 , $$ а $$lambda_1^2+lambda_2^2+lambda_3^2= left(lambda_1+lambda_2+lambda_3 right)^2-2, (lambda_1lambda_2+ lambda_1lambda_3+lambda_2lambda_3) .$$ Далее применяем формулы Виета.

Ответ. $ 3,a_3-a_1a_2-a_1^2+2, a_2 $.

Существуют общие алгоритмы нахождения полинома $ <mathfrak F>$ по заданному полиному $ Phi $: см. [3], [4]. Однако в своей практике я встречал необходимость в подобном представлении лишь для некоторых классов полиномов $ Phi_<> $; сейчас их и рассмотрим.

Суммы Ньютона

Для полинома $ f(x)=a_<0>x^n+a_1x^+dots+a_n, (a_0ne 0) $ его $ k_<> $-й суммой Ньютона называется сумма $ k_<> $-х степеней его корней: $$ s_k=lambda_1^k + dots + lambda_n^k . $$ При этом обычно считают $ k_<> in <mathbb N>$ (хотя формально можно определить суммы Ньютона и для отрицательных индексов $ k_<> $ при условии $ a_ ne 0 $). Для однообразия полагают также $ s_<0>=n $.

Теорема. Суммы Ньютона выражаются рационально через коэффициенты полинома $ f_<>(x) $ посредством следующих рекуррентных формул Ньютона:

Пример.

$$ s_2=(a_1^2-2, a_0a_2) big/ a_0^2 , $$ $$ s_3=-(a_1s_2+a_2s_1+3,a_3)big/ a_0= $$ $$ =-left(a_1 (a_1^2-2, a_0a_2) big/ a_0^2 +a_2 (-a_1 big/ a_0)+3,a_3 right) big/ a_0= $$ $$ =left(-a_1^3+3,a_0a_1a_2-3,a_0^2a_3 right) big/ a_0^3 . $$ ♦

Подробнее о суммах Ньютона ☞ ЗДЕСЬ.

Результант и дискриминант

Пусть $ g(x)=b_0x^m+dots + b_ $ — произвольный полином из $ mathbb A_<> [x] $. Тогда выражение $$ g(lambda_1) times dots times g(lambda_n) $$ является симметрическим полиномом от корней $ lambda_<1>,dots,lambda_n $ полинома $ f_<>(x) $. По теореме Гаусса, оно должно рационально выражаться через коэффициенты $ a_<0>,dots,a_n $. С другой стороны, очевидно, это выражение обращается в нуль тогда и только тогда, когда хотя бы один сомножитель обратится в нуль, т.е. будет существовать общий корень полиномов $ f_<>(x) $ и $ g_<>(x) $. Выражение $$ a_0^m prod_^n g(lambda_j) $$ называется результантом полиномов $ f_<>(x) $ и $ g_<>(x) $.

Способы вычисления результанта, его свойства и применения ☞ ЗДЕСЬ.

В частном случае, когда $ g_<>(x) $ совпадает с производной полинома $ f_<>(x) $ результант переходит в дискриминант — выражение отличающееся от $$ a_0^ prod_^n f^<prime>(lambda_j) $$ только сомножителем $ (-1)^/a_0 $ и обращающееся в нуль тогда и только тогда, когда $ f^<prime>(x) $ имеет общий корень с $ f_<>(x) $. Как мы увидим НИЖЕ, последнее условие оказывается необходимым и достаточным наличия у полинома $ f_<>(x) $ кратного корня.

Пример. Для $ f(x)=a_<0>x^2+a_1x+a_2 $ указанное произведение оказывается равным

$$ (2a_0lambda_1 +a_1)(2a_0lambda_2 +a_1)=(4a_0^2lambda_1 lambda_2+2a_0a_1(lambda_1 +lambda_2)+a_1^2)= $$ $$ =left(4a_0^2 frac-2a_0a_1frac+a_1^2right)=4a_0a_2-a_1^2, $$ т.е. привычному «школьному» понятию.

Способы вычисления дискриминанта, его свойства и применения ☞ ЗДЕСЬ.

Преобразования корней

Если $ lambda_<1>,dots,lambda_n $ — корни полинома $ f(x)=a_0x^n+a_1x^+dots+a_ $, то

1. корнями полинома $$ f(-x)=(-1)^nleft(a_0x^n-a_1x^+dots+(-1)^na_nright) = $$ $$ =(-1)^n sum_^n (-1)^ja_jx^ $$ являются $ -lambda_1, dots, -lambda_n $;

2. корнями полинома $$f(x- <coloralpha >)=a_0(x- <coloralpha > )^n+a_1(x- <coloralpha >)^+dots+a_n= $$ $$ = sum_^n a_j(x- <coloralpha >)^ $$ являются $ <coloralpha >+lambda_1, dots, <coloralpha >+lambda_n $;

3. при дополнительном условии, что $ a_ ne 0 $, корнями полинома $$f^<ast>(x)= x^nfleft(1/x right) equiv a_0+a_1x+dots+a_nx^n = $$ $$ =sum_^n a_jx^ $$ являются $ 1/<lambda_1>, dots, 1/ <lambda_n>$.

Преобразования 1-3 часто используются как при выводе теоретических результатов так и в практике вычислений.

Поясним идею этих применений. Корни исходного и корни преобразованного полинома остаются неизвестными. Допустим, мы получили какой-то результат, касающийся оценки положительных корней полинома $ f_<>(x) in mathbb R[x] $, и хотим распространить эту оценку и на отрицательные корни (см., к примеру, ☟ НИЖЕ ). Производится замена переменной $ x rightarrow — x $, которая меняет знаки всех корней: отрицательные становятся положительными, и к новому полиному применяется полученный результат. В приложениях возникают и более сложные преобразования корней: когда, к примеру, все их надо «загнать» в ограниченную область комплексной плоскости — скажем, в круг $ |x|le 1 $ (см. ☟ НИЖЕ ).

Пример. Построить полином $ F_<>(x) $, корни которого равны квадратам корней полинома $ f_<>(x) $.

Непрерывность корней

Теорема [5]. Корни полинома

$$ f(x)=x^n+a_1x^+dots+a_n in mathbb C[x],quad nge 1 $$ являются непрерывными функциями его коэффициентов. Строго говоря, если $ lambda_1,dots,lambda_ $ — корни этого полинома, а $ <tilde lambda_1>,dots, <tilde lambda_n>$ — корни полинома $$<tilde f>(x)=x^n+<tilde a>_1x^+dots+<tilde a>_n in mathbb C[x] , $$ то эти корни можно перенумеровать таким образом, чтобы $$ |lambda_j-<tilde lambda>_j| | | | | | . При увеличении значений $ <coloralpha >_<> $ от $ -2 $ до $ -1_<> $ происходит «дрейф» корней — плавный, но разный по скорости. К примеру, синий и фиолетовый корни меняются очень медленно, а вот зеленый и малиновый быстро сближаются пока не столкнутся при значении $ <coloralpha >=-1 $: $$ lambda_1approx -1.5096-0.4133 <mathbf i>, lambda_2 approx -0.6768+0.1479 <mathbf i>, lambda_3 approx 0.4364-0.4845 <mathbf i>, lambda_4 = 1+ <mathbf i>, $$ $$ lambda_5 =1+ <mathbf i> . $$ Что происходит при дальнейшем увеличении $ <coloralpha >_<> $? Число корней должно остаться инвариантным — по основной теореме высшей алгебры оно продолжает совпадать со степенью полинома, т.е. корни не аннигилируют. Поэтому столкнувшиеся корни порождают два новых — голубой и коричневый — которые начинают расходиться. При $ <coloralpha >=1 $ ситуация следующая: $$ lambda_1 approx -2.3350+0.4836 <mathbf i>, lambda_2 approx -0.5794+0.1185<mathbf i>, lambda_3 approx 0.2721-0.4926 <mathbf i>, $$ $$ lambda_4 approx -0.3888+2.5945 <mathbf i>, lambda_5 approx 0.5832+0.3480 <mathbf i>. $$ Имея перед глазами полную картину истории, понимаем, что корни, обозначенные $ lambda_ <1>$ (красный) и $ lambda_ <4>$ (голубой), стремятся к столкновению — и оно действительно происходит при $ <coloralpha >=2 $: $$ lambda_1 = -2+2<mathbf i>, lambda_2 approx -0.5458+0.1142 <mathbf i>, lambda_3 approx 0.2296-0.4712 <mathbf i>, lambda_4 = -2+2<mathbf i>, $$ $$ lambda_5 approx 0.5193+0.3101 <mathbf i>. $$ Дальнейшую динамику можем предсказать «по прецеденту» — столкнувшиеся корни должны разойтись. При $ <coloralpha >=3_<> $: $$ lambda_1 approx -4.0682+3.6140 <mathbf i>, lambda_2 approx -0.5184+0.1116 <mathbf i>, lambda_3 approx 0.2007-0.4506<mathbf i>, $$ $$ lambda_4 approx -1.2359+1.2927<mathbf i>, lambda_5 approx 0.4759+0.2864 <mathbf i>. $$ ♦

К какому числу стремится желтый корень при $ <coloralpha > to +infty $ ?

Последний пример наводит на еще одну гипотезу: мы видим, что графики корней получились гладкими, за исключением, возможно, некоторых специфических точек.

Теорема. Корни полинома

$$ f(x)=x^n+a_1x^+dots+a_n in mathbb C[x] $$ являются непрерывно дифференцируемыми функциями коэффициентов за исключением тех наборов значений коэффициентов, которые определяют кратные корни.

Доказательство ☞ ЗДЕСЬ.

Условие наличия кратного корня у полинома $ f_<>(x) $ может быть получено в виде явного условия на его коэффициенты. См. ☞ ДИСКРИМИНАНТ.

Поиск корней алгебраических уравнений: решение в радикалах

Можно ли выразить корни полинома $ f(x)in mathbb C[x] $ в виде «хороших» функций от его коэффициентов? Вспомним, что для квадратного уравнения существует общая формула вычисления корней: $$x^2+ax+b=0 Rightarrow lambda_<1,2>=frac<-apm sqrt> <2> . $$ Эта формула включает в себя элементарные алгебраические операции $ +,- ,times, div $ и операцию извлечения квадратного корня. По аналогии можно сформулировать и общую задачу.

Задача. Найти выражения корней полинома степени $ n_<>>2 $ в виде функций его коэффициентов; при этом функции должны представлять конечную комбинацию элементарных алгебраических операций и операций извлечения корней произвольных (целых) степеней.

Поставленная задача называется задачей о разрешимости уравнения в радикалах 6) .

Оказывается, что любое уравнение третьей или четвертой степени разрешимо в радикалах. Перед тем, как изложить способы их решения, сделаем два упрощения. Первое из них заключается в том, что уравнение $ f_<>(x)=0 $ делится на старший коэффициент полинома $ f_<>(x) $.

Полином называется нормализованным 7) , если его старший коэффициент равен $ 1_<> $. Операция деления полинома на его старший коэффициент называется нормализацией полинома.

Очевидно, что нормализованный полином имеет те же корни, и в тех же кратностях, что и исходный. Для простоты обозначений, будем считать, что полином уже нормализован: $$ f(x)=x^n+a_1x^+dots+a_n .$$

Второе упрощение заключается в замене переменной (подстановке): $ x=y+ <coloralpha > $. Ее результатом будет новый полином той же степени, что и исходный, относительно переменной $ y_<> $: $$ F(y)equiv f(y+ <coloralpha >) , . $$ Корни нового полинома связаны (cм. преобразование 2 ☞ ЗДЕСЬ ) с корнями старого по формуле $ lambda_j = Lambda_j+ <coloralpha > $; так что, найдя корни одного полинома, легко установим и корни другого. Подберем теперь параметр $ <coloralpha > $ так, чтобы обратить в нуль коэффициент при $ y^ $ в полиноме $ F_<>(y) $. Используя формулу бинома Ньютона, получаем $$ begin f(x)&=&x^n+a_1x^+a_2x^+dots+a_n= \ &=&(y+ <coloralpha >)^n +a_1(y+ <coloralpha >)^+a_2(y+ <coloralpha >)^+dots+a_n = \ &=&y^n + C_n^1 <coloralpha > y^ +C_n^2 <coloralpha >^2 y^+dots+ <coloralpha >^n + \ & & qquad + a_1y^+a_1 C_^1 <coloralpha > y^+dots +a_1 <coloralpha >^ + \ & & quad qquad qquad +a_2y^ + dots + a_n. end $$ Понятно, что если положить $ <coloralpha >= — a_1/n $, то коэффициент при $ y^ $ исчезнет. Для простоты обозначений, будем считать, что полином уже предварительно подвергнут такому преобразованию: $$ f(x)=x^n qquad +a_2x^+dots+a_n .$$

Уравнение третьей степени

Рассмотрим уравнение третьей степени: $$ x^3+p,x+q=0 $$ Сделаем в этом уравнении замену переменной: $ x=u+v $, введя две неизвестные $ u_<> $ и $ v_<> $; получим: $$ u^3+v^3+3,uv(u+v)+p(u+v)+q=0 . $$ Сгруппируем: $$ u^3+v^3+(3,uv+p)(u+v)+q=0 . $$ Подчиним теперь неизвестные $ u_<> $ и $ v_<> $ условию $$ 3,uv+p=0 iff uv=-frac

<3> . $$ Тогда предыдущее уравнение приведется к виду $$u^3+v^3=-q . $$ Итак, для определения неизвестных величин $ u_<> $ и $ v_<> $ мы получили систему уравнений $$ u^3+v^3=-q, uv=-frac

<3>. $$ Возведя последнее уравнение в куб, получим $$ u^3v^3=-frac <27> . $$ Два полученных равенства, связывающие $ u^3 $ и $ v^3 $, позволяет утверждать, что эти величины являются решениями квадратного уравнения: $$t^2+q,t- frac<27>=0 .$$

Выражение $$ Delta = frac<4>+frac <27>$$ называется дискриминантом кубического уравнения.

Решив квадратное уравнение, получим: $$ u^3=-frac<2>+ sqrt<Delta>, v^3=-frac<2>- sqrt <Delta> . $$ В итоге имеем формулу для решений уравнения: $$ x=u+v=sqrt[3]<-frac<2>+sqrt<frac<4>+frac<27>>>+ sqrt[3]<-frac<2>-sqrt<frac<4>+frac<27>>> ; $$ она называется формулой Кардано.

Формула Кардано не очень удобна для практических вычислений. Вспомним, что корень кубический из комплексного числа может принимать три различных значения. Решение же, представленное формулой Кардано, имеет в правой части комбинацию из двух кубических корней. Таким образом, получаем 9 всевозможных комбинаций из значений корней кубических. С другой стороны, основная теорема высшей алгебры утверждает, что кубическое уравнение должно иметь только три решения. Для того, чтобы установить соответствие между значениями $ u_<> $ и $ v_<> $, обратимся к условию $ uv=-p/3 $ . Согласно этому условию, задание значений для $ u_<> $ позволит однозначно восстановить $ v_<> $. Пусть $$ u_1=sqrt[3]<-frac<2>+sqrt<frac<4>+frac<27>>> $$ какое-то одно из трех возможных значений корня кубического. Два оставшихся значения корня кубического получаются домножением $ u_1 $ на корни кубические из единицы: $$u_2=u_1varepsilon_1, u_3=u_1varepsilon_2 $$ при $$varepsilon_1=cos frac<2pi> <3>+ <mathbf i>sin frac<2pi><3>= frac<-1><2>+ <mathbf i>frac<sqrt<3>> <2> u varepsilon_2=cos frac<4pi> <3>+ <mathbf i>sin frac<4pi><3>= frac<-1><2>- <mathbf i>frac< sqrt<3>> < 2> . $$ Если теперь взять $$ v_1=-frac

<3u_1> , $$ то решения кубического уравнения можно выразить в виде комбинаций $ u_1 $ и $ v_1 $: $$ begin lambda_1&=&u_1+v_1, \ lambda_2&=&u_2+v_2=u_2-frac<displaystyle p><displaystyle 3u_2>=u_1varepsilon_1-frac<displaystyle p> <displaystyle 3u_1varepsilon_1>=u_1varepsilon_1-frac<displaystyle pvarepsilon_2><displaystyle 3u_1>=u_1varepsilon_1+v_1varepsilon_2,\ lambda_3&=&u_3+v_3=u_1varepsilon_2+v_1varepsilon_1 . end $$ Окончательно получаем формулы для вычисления корней: $$ left< begin lambda_1&=&u_1+v_1, \ lambda_2&=&-frac<scriptstyle 1><scriptstyle 2>(u_1+v_1) + <mathbf i>frac<scriptstyle sqrt<3>> <scriptstyle 2>(u_1-v_1),\ lambda_3&=&-frac<scriptstyle 1><scriptstyle 2>(u_1+v_1) — <mathbf i>frac<scriptstyle sqrt<3>> <scriptstyle 2>(u_1-v_1), end right. $$ где $ u_1 $ — одно из значений корня кубического, а $ v_1 $ связано с ним соотношением $ v_1=-p/(3u_1) $.

Пример [2]. Решить уравнение $ x^3-6<mathbf i>,x^2-10,x+8 <mathbf i>=0 $.

Решение. Подстановка $ x=y+2 <mathbf i>$ приводит уравнение к виду $$y^3+2,y+4 <mathbf i>=0 , $$ т.е. $ p=2,,q=4 <mathbf i>$. Далее $$Delta=-frac<100> <27> Rightarrow sqrt <Delta>= pm frac<10 <mathbf i>><3sqrt<3>> Rightarrow u_1=sqrt[3]<left(-2 + frac<10><3sqrt<3>> right)<mathbf i>> . $$ Одно из значений последнего корня: $$u_1=-<mathbf i>, sqrt[3]<-2 + frac<10><3sqrt<3>>> , $$ это выражение можно упростить, если повезет заметить, что подкоренное выражение равно $ left(-1+1/<sqrt<3>>right)^3 $: $$u_1=<mathbf i>left(1-frac<1><sqrt<3>>right) Rightarrow v_1=-frac

<3u_1>= <mathbf i>left(1+frac<1><sqrt<3>>right) . $$ Получаем: $$mu_1=2, <mathbf i>, mu_2=1- <mathbf i>, mu_3=-1- <mathbf i> .$$ Значения корней исходного уравнения получатся «сдвигом» на $ 2 <mathbf i>$.

Дальнейший анализ формулы Кардано ☞ ЗДЕСЬ

Уравнение четвертой степени

$ x^4+a_1x^3+a_2x^2+a_3x+a_4 = 0 $ также может быть решено в радикалах. Идея решения заключается в сведении задачи к решению некоторого кубического уравнения. Ее реализация ☞ ЗДЕСЬ.

Уравнения высших степеней

Успех в решении уравнений третьей и четвертой степени побудил исследователей искать подобные формулы для уравнений высших степеней. Методология подхода была очевидна: свести решение уравнения $ n $-й степени к решению уравнения $ (n-1) $-й степени. Однако, несмотря на почти трехвековые усилия лучших математиков, решить уравнение пятой степени не удавалось. Наконец, в начале XIX века был получен отрицательный результат.

Теорема [Руффини, Абель]. Уравнение степени выше четвертой в общем случае неразрешимо в радикалах.

Пример. Уравнение $ x^5-4, x -2=0 $ не разрешимо в радикалах.

Установить разрешимо или нет данное конкретное уравнение в радикалах возможно с помощью теории, развитой французским математиком Галуа.

Пример. Уравнение $ x^5+x+1=0 $ разрешимо в радикалах, поскольку

Отрицательный характер результата теоремы Руффини-Абеля не должен слишком уж разочаровывать. Он означает только лишь то, что корни полинома нельзя представить в виде формулы, состоящей из конечного набора сравнительно простых функций. Тем не менее, если расширить класс допустимых в формуле функций (или допустить бесконечность числа операций), представление для корня можно найти (см., к примеру, ☞ ЗДЕСЬ ). Наконец, для практических задач часто более важна не столько «красивая» аналитическая формула для корня, сколько приближенное его значение с требуемой точностью.

Поиск корней алгебраических уравнений: возможность упрощений

Для некоторых классов уравнений удается упростить задачу: свести решение исходного уравнения к решению уравнения меньшей степени .

Возвратное уравнение

Так называется уравнение вида $ a_0z^n+a_1z^+dots+a_z+a_n=0, a_0ne 0 $, у которого набор коэффициентов $ (a_0,a_1,dots, a_,a_n) $ симметричен относительно середины: $$ a_0=a_,a_1=a_,dots, a_=a_ dots $$

Пример. Уравнения

$$ z^2-3,z+1=0,quad -sqrt<2>z^5+2,z^4+mathbf i z^3+2,z-sqrt<2>,quad z^n+1=0 , $$ $$ z^n+z^+z^+dots + z^2 +z+1=0 $$ являются возвратными.

Методы упрощения подобных уравнений ☞ ЗДЕСЬ.

Делимость полиномов

Здесь $ mathbb A_<> $ означает какое-то из множеств $ mathbb Q, mathbb R $ или $ mathbb C_<> $.

Теорема. Для полиномов $ f_<>(x) $ и $ g(x)not equiv 0 $ из $ mathbb A[x] $ существует единственная пара полиномов $ q_<>(x) $ и $ r_<>(x) $ из $ mathbb A[x] $ таких, что

$$ f(x) equiv g(x) q(x) + r(x) quad mbox < и >quad deg r ☞ ЗДЕСЬ.

В этом представлении полином $ f_<>(x) $ называется делимым, $ g_<>(x) $ — делителем, $ r_<>(x) $ — остатком от деления $ f_<>(x) $ на $ g_<>(x) $, а $ q_<>(x) $ — частным 9) . При $ r(x) equiv 0 $, говорят, что полином $ f_<>(x) $ делится (нацело) на $ g_<>(x) $, а полином $ g_<>(x) $ называется делителем $ f_<>(x) $. Тривиальными делителями полинома $ f_<>(x) $ называют сам полином $ f_<>(x) $ и полином тождественно равный $ 1_<> $ (оба — с точностью до домножения на ненулевую константу). Любой другой делитель полинома (если существует) называется нетривиальным.

Пример [1]. Найти частное и остаток от деления

$$f(x)=2, x^5 +x^4 -x^2 +2, x +1 quad mbox < на >quad g(x)=x^3+2, x^2 — x -1 .$$

Ответ. $ q(x)=2, x^2 -3, x + 8, r(x)=-18, x^2 + 7, x +9 $.

Фактическое выполнение операции деления полиномов можно производить, действуя лишь над наборами их коэффициентов — подобно тому, как мы производили их умножение.

Пример. Найти частное и остаток от деления

$$f(x)=x^8+x^7+3,x^4-1 quad mbox < на >quad g(x)=x^4-3, x^3 +4, x +1 .$$

Решение. $$ begin 1& 1 &0&0&3&0 &0 & 0&-1 &&1 -3 0 4 1\ 1&-3 &0&4&1& & & & && overline < 1 4 12 32 82>\ hline &4 & 0 &-4 & 2 & 0 & <> \ &4 &-12& 0 & 16 & 4& <> \ hline && 12& -4 &-14 & -4 & 0 & <> \ && 12& -36 & 0 & 48 & 12 & <> \ hline &&& 32 & -14& -52&-12 & 0 & <> \ &&& 32 & -96& 0 & 128& 32 & <> \ hline &&&&82&-52&-140&-32&-1 \ &&&&82&-246&0&328&82 \ hline &&&&&194&-140&-360&-83 end $$

Ответ. $ q(x)=x^4+4,x^3+12,x^2+32, x+82,, r(x)=194, x^3-140, x^2-360, x -83 $.

Свойства.

1. Если $ m le n $ при $ a_0ne 0, b_0 ne 0 $, то $ deg q(x) =n-m $ и ведущий член $ q_<>(x) $ равен $ /, x^ $.

2. Если $ g(x)equiv x-c $, то коэффициенты частного $ q_<>(x) $ найдутся из схемы Хорнера.

Наибольший общий делитель

Рассмотрим множество всех общих делителей полиномов $ f_<>(x) $ и $ g_<>(x) $: $$ mathbb D= d_1(x), g(x) mbox < делится на > d_1(x) > . $$ Наибольшим общим делителем полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином $ d_<>(x) $, который является делителем как $ f_<>(x) $, так и $ g_<>(x) $ и, вместе с тем, сам делится на любой другой общий делитель этих полиномов: $$ operatorname (f(x),g(x)) = d(x) iff d(x) in mathbb D , d(x) mbox< делится на > forall d_1(x) in mathbb D . $$ Рассмотрим множество всех полиномов, которые делятся и на $ f_<>(x) $ и на $ g_<>(x) $: $$ mathbb K= f(x), k_1(x) mbox < делится на > g(x) > . $$ Наименьшим общим кратным полиномов $ f_<>(x) $ и $ g_<>(x) $ называется полином $ k_<>(x) $, который делится как на $ f_<>(x) $, так и на $ g_<>(x) $ и, вместе с тем, сам является делителем любого другого полинома, который делится на $ f_<>(x) $ и $ g_<>(x) $: $$ operatorname (f(x),g(x)) = k(x) iff k(x) in mathbb K , forall k_1(x) in mathbb K mbox< делится на > k(x) . $$ Пока открытым является вопрос существования $ operatorname (f,g)_<> $ и $ operatorname (f,g)_<> $. Для первого случая этот вопрос решается конструктивно — построением $ operatorname (f,g)_<> $ с помощью алгоритма, позаимствованного из ☞ ТЕОРИИ ЧИСЕЛ.

Пусть $ f(x) not equiv 0 $ и $ g(x) not equiv 0 $ — полиномы из $ mathbb A_<>[x] $ . Поделим $ f_<>(x) $ на $ g_<>(x) $: $ f(x)=g(x)q_<1>(x)+r_1(x) $, пусть остаток $ r_<1>(x) not equiv 0 $, тогда $ 0 le deg r_<1>(x)

Теорема. Последний не равный нулю остаток в алгоритме Евклида совпадает с $ operatorname(f(x),g_<>(x)) $.

Доказательство полностью аналогично доказательству соответствующего результата из теории целых чисел. ♦

Пример. Вычислить

$$ operatorname left( x^4+3, x^3 -x^2 -4, x -3, , 3, x^3 +10, x^2 +2, x -3 right) , . $$

Решение. $$ begin x^4 &+3,x^3 &-x^2 &-4,x &-3 && 3,x^3+10,x^2+2,x-3\ x^4&+10/3, x^3&+2/3, x^2&-, x & && overline < 1/3 x -1/9 quad >\ hline &-1/3,x^3&- 5/3,x^2&-3,x&-3 \ &-1/3,x^3&-10/9,x^2& -2/9,x&<> +1/3 \ hline &&-5/9,,x^2& -25/9,x&-10/3 end $$ В обозначениях алгоритма Евклида, имеем: $$ q_<1>(x)=1/3, x -1/9, r_<1>(x)=-5/9, x^2 -25/9, x-10/3 . $$ Поскольку $ r_<1>(x) notequiv 0 $, делим $ g_<>(x) $ на этот остаток: $$ begin 3,x^3 &+10,x^2 &+2,x &-3 && -5/9,,x^2 -25/9,x-10/3 \ 3, x^3&+15, x^2&+18, x & &&, overline <-27/5, x +9 quad >\ hline &-5,x^2&-16,x&-3 \ &-5,x^2&-25,x&-30 \ hline &&9,x&+27 end $$ Здесь $ q_<2>(x)=-27/5, x +9, r_2(x)=9x+27 notequiv 0 $ и алгоритм деления продолжается: $$ begin -5/9,,x^2& -25/9,x& -10/3 && 9,x+27 \ -5/9,,x^2& -5/3,x& && , overline < -5/81, x — 10/81 quad >\ hline &-10/9,x& -10/3 \ &-10/9,x&-10/3 \ hline & & 0 end $$ Здесь остаток получился равным нулю, следовательно $ r_<2>(x)=operatorname(f(x),g(x)) $.

Ответ. $ 9(x+3)_<> $.

Еще один способ нахождения $ operatorname $ для полиномов из $ mathbb[x] $ вытекает из основной теоремы высшей алгебры.

Теорема. Пусть множество $ < (x-lambda_1),dots,(x-lambda_<mathfrak r>) > $ представляет собой объединение множеств линейных сомножителей полиномов $ f_1(x),dots,f_k(x) $. Выпишем «универсальное» разложение каждого $ f_j $ на линейные сомножители:

Пример. Вычислить $ operatorname left(x^2-1,, x^3+1 right) $ .

Решение. Выписываем разложения полиномов на линейные сомножители: $$x^2-1equiv (x-1)(x+1), quad x^3+1 equiv(x+1) left(x-left( 1/2 — sqrt<3>/2 mathbf right) right) left(x- left( 1/2 + sqrt<3>/2 mathbf right) right) .$$

Ответ. $ x+1 $.

Теорема. Существуют полиномы $ u(x)_<> $ и $ v(x)_<> $ из $ mathbb A[x] $, удовлетворяющие уравнению линейного представления $ operatorname $:

Доказательство этого результата и практический способ построения полиномов $ u(x)_<> $ и $ v(x)_<> $ можно скопировать из соответствующего раздела теории чисел.

Явное представление $ operatorname (f(x),g(x)) $ через коэффициенты полиномов с помощью аппарата определителей приведено ☞ ЗДЕСЬ.

Взаимно простые полиномы

— это полиномы, у которых нормализованный $ operatorname $ равен $ 1_<> $ (тождественно). Подробное рассмотрение этого случая ☞ ЗДЕСЬ.

Производные от полинома

Для случая произвольной функции $ F(x): mathbb R mapsto mathbb R $ это определение строится на предельном переходе: $$ frac bigg|_<_> = F^<prime>(c) = lim_ frac .$$ Пусть $ F(x)equiv x^k $ при $ kin mathbb N_<> $. Тогда, с помощью формулы бинома Ньютона получаем: $$(c+h)^k-c^k=kc^h+C_k^2c^h^2+dots+h^k $$ и $$frac to kc^ quad npu hto 0 . $$ Отсюда следует, что функция $ x^ $ дифференцируема в любой точке $ xinmathbb R_<> $ и ее производная равна $ kx^ $. Обобщим это определение и на комплексную плоскость $ mathbb C^<> $ . Всюду в предыдущих рассуждениях допустим, что и точка $ c_<> $ и приращение $ h_<> $ могут быть комплексными. Окончательный вывод не изменится: формула $$(x^k)^<prime>= kx^ $$ остается справедливой и для $ xin mathbb C_<> $. С помощью этой формулы, а также с помощью основных правил дифференцирования функций: $$ left(F_1pm F_2 right)^<prime>=F_1^<prime>pm F_2^<prime>, left(cFright)^<prime>=cF^<prime>, left(F_1F_2 right)^<prime>=F_1^<prime>F_2+F_1F_2^ <prime>$$ получаем $$ f^<prime>(x)=(a_0x^n+a_1x^+dots+a_x+a_n)^ <prime>= na_0x^+(n-1)a_1x^+dots +a_ . $$ Таким образом, $ f^<prime>(x) $ также будет полиномом над $ mathbb A_<> $ и $ deg f^ <prime>= deg f — 1 $. Кроме того, обобщая по индукции формулу дифференцирования произведения, выводим: $$ left(f_1f_2times dots times f_k right)^<prime>= f_1^<prime>f_2times dots times f_k+f_1f_2^<prime>times dots times f_k+ dots+ f_1f_2times dots times f_k^ <prime>. $$ Если применить ее к формуле разложения полинома на линейные множители, то получим формулу $$ begin f^<prime>(x)&=&a_0(x-lambda_2)(x-lambda_3)times dots times (x-lambda_n)+ \ &+&a_0(x-lambda_1)(x-lambda_3)times dots times (x-lambda_n)+ \ &+ & dots + \ &+& a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_). end $$ Из нее, в частности, следует, что $$ f^<prime>(lambda_j)=a_0(lambda_j-lambda_1)times dots times (lambda_j-lambda_)(lambda_j-lambda_) times dots times (lambda_j-lambda_)= a_0 prod_ <1le k le n atop scriptstyle kne j>(lambda_j — lambda_k) . $$ Последняя формула, впрочем, может быть получена и напрямую из определения производной: $$ f^<prime>(lambda_j)=lim_ frac =lim_ frac . $$ Производные высших порядков вводятся определением $$F^<(k)>(x)= left(F^<(k-1)>(x) right)^ <prime> npu k>1 ; $$ для однотипности обозначений считают также нулевой производной сам полином: $$F^<(0)>(x)= F(x) .$$ В дальнейшем нам пригодится следующая формула Лейбница: $$left(F_1 F_2 right)^<(k)>=sum_^k C_k^j F_1^<(k-j)>F_2^ <(j)>=F_1^<(k)>F_2+ C_k^1F_1^<(k-1)>F_2^ <prime>+ C_k^2F_1^<(k-2)>F_2^<prime prime >+ dots +F_1F_2^ <(k)> , $$ где $ C_k^ $ означает биномиальный коэффициент.

Для полинома $ f(x)_<> $ степени $ n_<> $ имеем: $$f^<(k)>(x)=n(n-1)times dots times (n-k+1)a_0x^+dots+k!a_ npu kle n $$ и $ deg f^ <(k)>= deg f — k $. Очевидно $ f^<(k)>(x)equiv 0 $ при $ k> n_<> $.

Теорема. Простой корень полинома не является корнем его производной. Кратный корень полинома кратности $ mathfrak m $ является корнем его производной кратности $ (<mathfrak m>-1) $.

Доказательство. Если $ x=lambda_<> in mathbb C $ — простой корень для $ f_<>(x) $, то $ f(x)equiv (x-lambda)tilde(x) $ при $ tilde(lambda) ne 0 $. Дифференцируя и подставляя $ x=lambda $, получаем $$ f^<prime>(x)equiv tilde(x) +(x-lambda)tilde^<prime>(x) Rightarrow f^<prime>(lambda)=tilde(lambda)ne 0 $$ по предположению.

Если $ x=lambda_<> $ — кратный корень кратности $ mathfrak m $ для $ f_<>(x) $, то $ f(x)equiv (x-lambda)^<mathfrak m>widehat(x) $ при $ widehat(lambda) ne 0 $. Снова дифференцируем: $$ f^<prime>(x)=<mathfrak m>(x-lambda)^<<mathfrak m>-1> widehat(x)+ (x-lambda)^<<mathfrak m>>widehat^<prime>(x)= (x-lambda)^<<mathfrak m>-1> underbrace<left(<mathfrak m>widehat(x) +(x-lambda)widehat^<prime>(x) right)>_ <= H(x)> . $$ Из этого представления следует, что $ x=lambda_<> $ является корнем $ f^<prime>(x) $ кратности, не меньшей $ (<mathfrak m>-1) $. Если бы кратность была больше этого значения, то необходимо $ H(lambda)=0 $. Однако, этого не может быть, т.к. $ widehat(lambda) ne 0 $. ♦

Полином $ f(x)_<> $ имеет кратный корень тогда и только тогда, когда он имеет нетривиальный наибольший общий делитель со своей производной $$ operatorname (f(x),f^<prime>(x)) notequiv const . $$

Пример. При каком условии на коэффициенты $ p_<> $ и $ q_<> $ полином

$$ x^3+p,x+q $$ имеет кратный корень?

Решение. На основании теоремы на этом корне $ x=lambda_<> $ должно быть выполнено $$lambda^3+p,lambda+q=0 , quad 3, lambda^2 + p=0 .$$ Из второго равенства выражаем $ lambda^2 $ и подставляем в первое: $$lambda^2=-frac

<3> Rightarrow lambda left(-frac

<3>right) +p,lambda+q=0 Rightarrow lambda=-frac<3,q> <2,p>$$ при $ pne 0 $. Подставляя это значение в любое из исходных равенств, получаем: $$ frac<27,q^2+4,p^3> <4, p^2>=0 Rightarrow left(frac <2>right)^2 + left(frac

<3>right)^3 =0 . $$ Это условие уже встречалось нам ВЫШЕ при анализе формулы решения уравнения третьей степени. При $ p=0 $ кратный корень может встретиться лишь при $ q=0 $, т.е. опять же при обращении в нуль дискриминанта кубического уравнения.

Ответ. $ left( p/3 right)^3 + left( q/2 right)^2=0 $.

При каком условии на коэффициенты $ p_<> $ и $ q_<> $ полином

а) $ x^4+p,x+q $ ; б) $ x^5+p,x+q $

имеет кратный корень?

Пример. Найти все значения параметра $ <coloralpha > $, при которых полином

$$ x^4-5,x^2+ <coloralpha >,x+28 $$ имеет кратный корень.

Решение. На основании следствия к теореме для выполнения условия необходимо и достаточно, чтобы был нетривиален $ operatorname (f(x),f^<prime>(x)) $. Ищем его по алгоритму Евклида, делим $ f(x) $ на $ f^<prime>(x) $: $$ f(x)equiv frac<1> <4>, x, f^<prime>(x) + overbrace<left(-frac<5><2>, x^2 +frac<3><4>, <coloralpha >, x +28 right)>^ , $$ затем $ f^<prime>(x) $ на полученный остаток $ r_<1>(x) $: $$ f^<prime>(x) equiv left(-frac<8><5>,x- frac<12><25>, <coloralpha > right) r_1(x) + overbrace<left(frac<3><25>,(3, <coloralpha >^2 + 290),x+ frac<361><25>, <coloralpha > right)>^ , $$ и, при дополнительном предположении $ 3, <coloralpha >^2 + 290ne 0 $, делим $ r_<1>(x) $ на $ r_<2>(x) $: $$ r_1(x) equiv frac<25> <36left(3, <coloralpha >^2 +290 right)^2> left[-30,left(3, <coloralpha >^2 +290 right) x + alpha, (27, <coloralpha >^2 + 6220) right] r_2(x) + $$ $$ + frac <25, left(-27, <coloralpha >^4 -19660, <coloralpha >^2 + 3390912right) > <36, left(3, <coloralpha >^2 +290 right)^2> . $$ $ operatorname (f(x),f^<prime>(x)) $ может быть нетривиальным (равным $ r_<2>(x) $) только при условии $$-27, <coloralpha >^4 -19660, <coloralpha >^2 + 3390912=0 . $$ Решить последнее уравнение легко если заменить переменную $ A = <coloralpha >^2 $: $$( A-144)(27, A +23548)=0 .$$

При $ 3, <coloralpha >^2 + 290= 0 $ будет $ operatorname (f(x),f^<prime>(x))= r_2(x)not equiv 0 $, так что при этих значениях параметра кратных корней у $ f(x)_<> $ быть не может.

Число $ lambda_<> $ является корнем кратности $ mathfrak m_<> $ для $ f(x)_<> $ тогда и только тогда, когда выполнены условия:

Доказательство необходимости следует из теоремы. Достаточность вытекает из результатов следующего пункта (формализация способа проверки приводится ☞ ЗДЕСЬ).

Формула Тейлора

Представление полинома $ f(x)_<>in mathbb A[x] $ в канонической форме $ a_<0>x^n+a_1x^+dots + a_n $ не является единственно возможным способом задания полинома. В конце концов, полином можно представить и с помощью разложения на линейные сомножители — разумеется, если известен набор его корней. Саму эту каноническую форму можно описать как разложение полинома по степеням переменной $ x_<> $. Пусть теперь $ cin mathbb A_<> $ — произвольная константа. Любую степень $ x^ $ можно «переразложить» по степеням линейного полинома $ x-c_<> $ с помощью формулы бинома Ньютона: $$ x^kequiv left[c+(x-c) right]^kequiv c^k +kc^(x-c)+ frac<2>c^(x-c)^2+dots+ (x-c)^k .$$ Если это сделать для каждого монома полинома $ f(x)_<> $, то получим разложение $ f(x)_<> $ по степеням $ x-c_<> $ в виде $$ f(x)equiv A_0+A_1(x-c)+A_2(x-c)^2+dots+A_n(x-c)^n . $$

Задача. Найти коэффициенты $ A_<0>,dots,A_n $ в этом разложении.

Для решения этой задачи продифференцируем несколько раз последнее тождество: $$ begin f^<prime>(x)&=&A_1+2,A_2(x-c)+3,A_3(x-c)^2+dots+nA_n(x-c)^ , ,\ f^<prime prime>(x)&=&2,A_2+3cdot 2,A_3(x-c)+dots +n(n-1)A_n(x-c)^, ,\ f^<prime prime prime>(x)&=&3cdot 2,A_3+dots +n(n-1)(n-2)A_n(x-c)^, ,\ dots & & dots end $$ Подстановка в эти формулы $ x=c_<> $ дает: $$f^<prime>(c)=A_1, f^<prime prime>(c)=2,A_2, f^<prime prime prime>(c)= 3cdot 2,A_3,dots $$

Теорема. Разложение полинома $ f_<>(x) $ по степеням $ x-c_<> $ имеет вид

$$ f(x) equiv f(c)+ frac(c)> <1!>(x-c) + frac(c)> <2!>(x-c)^2+ dots + frac(c)> (x-c)^ = $$ $$ =sum_^n frac(c)> (x-c)^ ; $$ это тождество называется формулой Тейлора для полинома $ f_<>(x) $ в точке $ x=c $.

Доказательство и алгоритм эффективного вычисления коэффициентов формулы Тейлора (схема Хорнера) ☞ ЗДЕСЬ.

На основании этих серий мы должны предсказать величину $ F(x)_<> $. Самой простой функцией, решающей задачи в таких постановках, является полином. Если этот полином $ f(x)_<> $ удается построить, то именно его мы и будем считать приближением неизвестной нам функции $ F(x)_<> $. Задача построения такого полинома для серии экспериментов первого типа обсуждается ☞ ЗДЕСЬ. А формула Тейлора позволяет найти полином $ f(x)_<> $ для серии экспериментов второго типа. Геометрически: неизвестный нам заранее график функции $ y=F(x)_<> $ (красный) приближается (аппроксимируется) либо прямой (зеленый), либо параболой (серый), либо кубикой (фиолетовый) — и все кривые приближения строятся только на основании информации о функции $ F(x)_<> $ в одной-единственной точке $ c_<> $.

Пример. Найти приближенное значение $ F(1)_<> $, если известно, что

Решение. По формуле Тейлора получаем полином $$f(x)=0.367+0.367(x+1) + frac<0.367> <2>(x+1)^2+frac<0.367> <6>(x+1)^3 $$ и $ f(1)=2.324(3) $.

Ответ. $ F(1)approx 2.324 $.

Полиномы с вещественными коэффициентами

Рассмотрим теперь случай полинома с вещественными коэффициентами $ f(x)=a_0x^n+a_1x^+ dots + a_n in mathbb R [x] $.

Теорема. Значения полинома $ f(x) in mathbb R [x] $ от комплексно-сопряженных значений переменной будут также комплексно-сопряженными:

$$ mbox <если> f(c)=A+mathbf i B mbox <при> subset mathbb R, mbox <то> f(overline)=A-mathbf i B , . $$

Доказательство. Действительно, поскольку $ a_jin mathbb R $, то $ overline=a_j $ для $ forall jin <0,1,dots,n>$, и тогда $$ begin fleft(overline right)&=&a_0 overline^n + a_1 overline^ + dots + a_n = overline overline + overline overline>+ dots + overline= \ &=&overline+ dots + a_n>=A-mathbf i B . end $$

Если мнимое число $ c=alpha + mathbf i beta , beta ne 0 $ является корнем $ f_<>(x) $, то и ему комплексно-сопряженное $ overline c = alpha — mathbf i beta $ также является корнем $ f_<>(x) $.

Иными словами, мнимые корни полинома $ f_<>(x) $ с вещественными коэффициентами «ходят пáрами»: $ alpha pm mathbf i beta $. Геометрический смысл: на комплексной плоскости точки, изображающие корни $ f_<>(x) $, расположены симметрично относительно вещественной оси.

Как следствие предыдущей теоремы и основной теоремы высшей алгебры, получим

Теорема. Любой полином $ f_<>(x)in mathbb R [x] $ может быть представлен в виде произведения вещественных полиномов степеней не выше второй:

$$ begin f(x) & equiv a_0 (x- lambda_1)^<<mathfrak m>_1> times dots times (x- lambda_r)^<<mathfrak m>_r> times \ & times (x^2 +p_1x+ q_1)^<<mathfrak M>_1> times dots times (x^2 +p_<ell>x+ q_<ell>)^<<mathfrak M>_<ell>> . end $$ Здесь $ lambda_1 , dots , lambda_r $ — различные вещественные числа, а квадратные трехчлены $$ x+ q_<ell>> subset mathbb R [x] $$ — различные с отрицательными дискриминантами $ mathcal D_j=p_j^2-4q_j

Полином $ f_<>(x) $ с вещественными коэффициентами нечетной степени имеет хотя бы один вещественный корень, а, в общем случае, нечетное число вещественных корней (с учетом их кратностей ).

Геометрия

Полиномы с вещественными коэффициентами удобны тем, что теоретические результаты, полученные в предыдущих пунктах, получают геометрическую интерпретацию. Прежде всего, следует отметить, что полином является частным случаем непрерывной функции и на него распространяются все результаты математического анализа, разработанные для подобных функций. Итак, полином $ f_<>(x) $ — непрерывная функция при любых $ x in mathbb R $. Более того, поскольку производные полинома снова оказываются полиномами, то свойство непрерывности наследуется при дифференцировании: полином является непрерывно-дифференцируемой функцией. Из этого следует, что на плоскости $ (x_<>,y) $ график полинома $ y=f_<>(x) $ представляет из себя непрерывную и гладкую кривую (ни разрывов, ни углов!) — касательная к графику существует в любой его точке.

Далее, вещественному корню $ x=lambda_<> $ полинома $ f_<>(x) $ на плоскости $ (x_<>,y) $ соответствует точка пересечения графика $ y=f_<>(x) $ с осью абсцисс.

По основной теореме высшей алгебры, таких точек может быть только конечное число: их — не более степени полинома $ deg f (x) $. Далее, между каждой парой $ lambda_j, lambda_k $ вещественных корней полинома $ f_<>(x) $, его график обязан иметь «впадину» или «горб». Обращаясь к языку математического анализа, можно сказать (и доказать), что между двумя вещественными корнями полинома находится точка его локального минимума или локального максимума. В этой точке касательная к графику функции параллельна оси абсцисс и, следовательно, тангенс угла наклона касательной должен быть равен нулю. Иными словами, точки $ mu_1,mu_2,dots $, в которых полином имеет локальный минимум или максимум, должны быть корнями его производной. См. следующий ПУНКТ.

К сожалению, не имеется наглядной интерпретации мнимых корней полинома .

Дальнейшие геометрические свойства полинома с вещественными коэффициентами см. ☞ ЗДЕСЬ.

Экстремумы

Говорят, что полином $ f(x)in mathbb R[x] $ имеет в точке $ c_<> $ (локальный) минимум если существует некоторое $ delta>0 $, что при всех значениях аргументов из $ delta_<> $-окрестности точки $ c_<> $, т.е. при всех $ x_<> $, удовлетворяющих неравенству $ |x-c| f(c) $. Если последнее неравенство изменить на противоположное, то получим определение (локального) максимума. Говорят, что полином имеет в точке $ c_<> $ (локальный) экстремум 10) если он имеет в этой точке либо максимум либо минимум.

Теорема [Ферма для полиномов]. Если полином $ f_<>(x) $ имеет в точке $ c_<> $ экстремум, то в этой точке его производная обращается в нуль: $$ f'(c)=0 . $$

Геометрический смысл этого результата пояснен в предыдущем пункте. Обращение производной полинома в нуль в точке $ c_<> $ является условием необходимым для существования в ней экстремума. Для выяснения будет ли в этой точке минимум, максимум или же экстремум отсутствует, следует обратиться к формуле Тейлора. Рассмотрим эту формулу в точке $ c_<> $ «подозрительной на экстремум», т.е. в такой, где $ f'(c)=0 $: $$ f(x)-f(c)=frac<1><2>f»(c)(x-c)^2+frac<1><6>f»'(c)(x-c)^3+dots+frac<1>f^<(n)>(c)(x-c)^n . $$ Если $ f»(c)ne 0 $, то можем переписать эту разность в виде $$ f(x)-f(c)=(x-c)^2underbrace<left[frac<1><2>f»(c)+frac<1><6>f»'(c)(x-c)+dots+frac<1>f^<(n)>(c)(x-c)^right]>_ . $$ Полином $ P(x) $ в точке $ c_<> $ имеет значение $ frac<1><2>f»(c) $, и его знак в некоторой окрестности точки $ c_<> $ полностью определяется знаком этого числа. Таким образом, в той же окрестности имеем: $$ operatorname (f(x)-f(c)) = operatorname (f»(c)) . $$

Если в точке $ c_<> $ выполнены условия $ f'(c)=0, f»(c)> 0 $ то в этой точке полином имеет локальный минимум; если же в ней выполнены условия $ f'(c)=0, f»(c) c \ — operatorname f»'(c) quad npu x нечетном $ k_<> $. При этом в точке $ c_<> $ полином будет иметь локальный минимум при $ f^<(k+1)>(c)>0 $ и локальный максимум при $ f^<(k+1)>(c) ☞ ЗДЕСЬ ), поэтому оценить корни полинома $ f'(x) $ мы можем, разве что, приближенно. После их нахождения, приближеные значения подставляются в полином $ f_<>(x) $ и ошибка вычислений накапливается… Можно ли избежать этого накопления? — Частично, да. Для полинома $ f_<>(x) $ (четной) степени $ n_<> $ можно построить новый полином степени $ n-1 $ по новой переменной $ z_<> $: $$ mathcal F(z) = (z-f(mu_1))times dots times(z-f(mu_)) , $$ где $ mu_1,dots,mu_ $ — корни $ f'(x) $. При этом коэффициенты нового полинома $ mathcal F(z) $ будут рационально выражаться через коэффициенты полинома $ f'(x) $ на основании теоремы Гаусса о симметрических полиномах. Подробности конструктивного построения см. ☞ ЗДЕСЬ. Как правило, максимальный вещественный корень полинома $ mathcal F(z) $ и будет давать значение $ max f(x) $.

Пример. Найти $ displaystyle max_ (-x^6+12,x^2+12,x+2) $.

Решение. Если идти по традиционной схеме математического анализа, то мы должны сначала найти корни производной полинома $ f(x)=-x^6+12,x^2+12,x+2 $, т.е. решить уравнение $ x^5-4,x-2=0 $. В радикалах это уравнение не решается, так что приходится применять приближенные методы поиска вещественных корней: $ mu_1approx -1.24359, mu_2 approx — 0.50849, mu_3 approx 1.51851 $. Наконец, требуется сравнить по величине $ f(mu_1), f(mu_2), f(mu_3) $.

В альтернативу этому подходу, можно избежать нахождения корней производной и построить (хоть и кропотливо, но зато безошибочно) полином $$ mathcal F(z)= -z^5+10,z^4+472,z^3+16208,z^2-16272,z-32800 , $$ найти один его (максимальный вещественный) корень $ approx 35.6321 $ — он и будет искомым максимумом.

Проверка: $ max f = f(mu_3) approx 35.6321 $.

Подчеркнем, что указанная возможность гарантирована только полиномиальностью рассматриваемой экстремальной задачи и на произвольные (неполиномиальные) функции предлагаемый метод не распространяется.

Приводимость

Полином $ Phi(x) in mathbb A[x] $, отличный от константы, называется неприводимым в (или неприводимым над) $ mathbb A_<> $ если у $ Phi(x) $ нет нетривиального делителя в $ mathbb A[x] $. В противном случае $ Phi(x) $ называется приводимым в (или приводимым над) $ mathbb A_<> $. Полином $ Phi(x) in mathbb A[x] $ неприводим над $ mathbb A_<> $ тогда и только тогда, когда $ operatorname (Phi(x),g(x)) equiv const in mathbb A_<> $ для любого полинома $ g(x)in mathbb A_<>[x], deg g(x) ♦

Теорема. Любой полином $ f(x)in mathbb R [x] $ степени большей $ 2_<> $ приводим в $ mathbb R_<> $. Неприводимыми в $ mathbb R_<> $ являются полиномы вида

$$ x+a quad mbox <и>quad x^2+p, x +q_<> quad mbox <при>quad subset mathbb R, p^2 — 4q ☞ ЗДЕСЬ .

Рассмотрим теперь полином с рациональными коэффициентами: $$f(x)=a_0x^n+a_1x^+dots+a_n in mathbb Q [x] , a_0 ne 0 . $$ Если полином $ f_<>(x) $ приводим в $ mathbb Q_<> $, то будет приводимым и полином $ Ccdot f_<>(x) $ при $ forall C in mathbb Q, C ne 0 $; верно и обратное. Представив коэффициенты $ a_<0>,dots, a_n $ в виде несократимых дробей, возьмем $$ C=operatorname(mbox< знаменатель > a_<0>,dots, mbox< знаменатель > a_n ) , $$ тогда приводимость (или неприводимость) полинома $ f_<>(x) $ в $ mathbb Q_<> $ эквивалентна приводимости (соответственно, неприводимости) в $ mathbb Q_<> $ полинома $ Ccdot f(x) $ с целыми коэффициентами. Поэтому в дальнейшем будем сразу предполагать $ f(x)in mathbb Z[x] $. Можно ли пойти дальше и утверждать, что приводимость такого полинома в $ mathbb Q_<> $ эквивалентна приводимости его в $ mathbb Z_<> $, т.е. полином раскладывается на произведение полиномов меньших степеней с рациональными коэффициентами тогда и только тогда, когда он раскладывается на произведение полиномов меньших степеней с целыми коэффициентами?

Теорема. Полином $ f(x)in mathbb Z[x] $ неприводимый в $ mathbb Z_<> $ будет неприводимым и в $ mathbb Q_<> $.

Приводимость полинома с целыми коэффициентами $ f(x)in mathbb Z[x] $ в $ mathbb Z_<> $ означает, что он раскладывается на два множителя с целыми коэффициентами: $$ a_0x^n+a_1x^+ dots + a_n equiv (b_0x^k+b_1x^ + dots + b_k) (c_0x^<ell>+c_1x^ <ell-1>+ dots + c_<ell>) $$ при $ k ☞ ЗДЕСЬ . ♦

Итак, для поиска рациональных корней полинома $ f_<>(x) $ надо выписать множество всех натуральных делителей $ <<mathfrak p>_1=1,dots,<mathfrak p>_> $ числа $ |a_n| $, и множество всех натуральных делителей $ <<mathfrak q>_1=1,dots,<mathfrak q>_> $ числа $ |a_0| $, и после этого организовать вычисление $ fleft(pm <mathfrak p>_j/<mathfrak q>_i right) $ при всех возможных значениях индексов $ jin <1,dots,s >, i in <1,dots, t >$. Если ни одно из полученных чисел не равно нулю, то рациональных корней полином не имеет.

Если нормализованный полином $ f(x) in mathbb Z[x] $ имеет рациональные корни, то они — только целые и находятся среди делителей свободного члена.

Пример. Найти рациональные корни полинома

Подробнее о приводимости и неприводимости полиномов в $ mathbb Z_<> $ ☞ ЗДЕСЬ.

Локализация корней

Границы расположения корней

Теорема [Маклорен]. 11) Все корни полинома

$$f(x)=a_0x^n+a_1x^+dots+a_n in mathbb C [x], a_0 ne 0$$ удовлетворяют неравенству $$ |lambda_j| 0$$ удовлетворяют неравенству $$ lambda_j положительные корни.

А как получить нижнюю оценку возможных отрицательных корней?

Это можно сделать с помощью преобразования 1 полинома, рассмотренного ☞ ЗДЕСЬ. В самом деле, отрицательные корни полинома $ f(x) $ являются положительными корнями полинома $ f(-x) $. Найдя верхнюю границу последних с помощью любого из приведенных выше критериев, мы меняем у нее знак и в результате получаем нижнюю оценку отрицательных корней $ f(x) $. Преобразование 3 , рассмотренное в том же пункте, позволяет получить отдельные интервалы для возможных положительных и отрицательных корней.

Пример. Найти оценки положительных и отрицательных корней полинома

$$ f(x)=x^8+2, x^7-2, x^6 +6, x^5 -80, x^4 + 100, x^3 -400, x^2 + 15, x +30 . $$

Решение. Сначала ограничим положительные корни сверху. В теореме Лагранжа имеем $ r=2,, A=400 $, следовательно $ lambda_j -401 $. Формируем полином $$ f^<ast>(x) = x^8f(1/x)= 1+2, x-2, x^2 +6, x^3 -80, x^4 + 100, x^5 -400, x^6 + 15, x^7 +30,x^8 $$ для оценки нижней границы положительных корней: $$1/lambda_j frac<1><1 +sqrt<40/3>> . $$ Наконец, оценка Лагранжа для полинома $ f^<ast>(-x) $: $$-1/lambda_j 12) .

Теорема [Декарт]. Число положительных корней полинома

$$f(x)=a_0x^n+a_1x^+dots+a_x+a_n in mathbb R[x], quad (a_0> 0,a_n ne 0)$$ с учетом их кратностей равно или меньше на четное число числа знакоперемен в ряду его коэффициентов: $$ operatorname < f(x)=0 mid x>0 > = <mathcal V>(a_0,a_1,dots,a_n)-2 k , quad kin <0,1,2, dots > . $$

Доказательство ☞ ЗДЕСЬ.

С помощью преобразования корней полинома (см. пункт 1 ☞ ЗДЕСЬ ) можно доказать следствие:

Число отрицательных корней полинома

$$f(x)=a_0x^n+a_1x^+dots+a_x+a_n, quad (a_0> 0,a_n ne 0)$$ с учетом их кратностей можно оценить по формуле $$ operatorname < f(x)=0 mid x 0 >=2-2k ge 0 ,$$ следовательно $ f_<>(x) $ имеет либо два, либо ни одного положительного корня. Далее, по следствию: $$ operatorname < f(x)=0 mid x

Если каким-то образом заранее известно, что все корни полинома вещественны, то число положительных из них определяется по правилу знаков Декарта однозначно:

Пример. Характеристический полином вещественной симметричной матрицы удовлетворяет условию следствия. См. ☞ ЗДЕСЬ.

Корни полинома в областях комплексной плоскости

Задача. Для полинома 14) $ f(z) $ получить точную информацию о числе его корней в заданной области $ mathbb S $ комплексной плоскости $ mathbb C $.

Оказывается, для достаточно широкого класса областей $ mathbb S $ эту информацию можно получить без применения численных, т.е. приближенных методов. Существуют алгоритмы, позволяющие за конечное число элементарных алгебраических операций ($ +,-,times, div $) над коэффициентами $ f(z) $ установить количество корней этого полинома в таких областях, как, к примеру, $$ begin mathbb S&=&< zin mathbb R big| a 15) на заданном интервале $ ]a,b[ $ если на этом интервале
1. cоседние полиномы $ f_j(x) $ и $ f_(x) $ не имеют общих корней;
2. $ f_K(x)ne 0 $;
3. если $ f_j(x_0)=0 $ при $ x_0 in ]a,b[ $ и $ jin <1,dots,k-1>$, то числа $ f_(x_0) $ и $ f_(x_0) $ имеют разные знаки: $ f_(x_0)f_(x_0) 4. произведение $ f_<0>(x)f_<1>(x) $ меняет знак с отрицательного на положительный когда $ x_<> $, возрастая, проходит корень $ lambdain ]a,b[ $ полинома $ f_0(x)equiv f(x) $.

Число знакоперемен $$ <mathcal V>_x= <mathcal V>(f_0(x), f_1(x),dots, f_K(x)) $$ при $ x_<> $ возрастающем от $ a_<> $ к $ b_<> $, будет меняться когда $ x_<> $ проходит через корень какого-либо полинома системы. Доказывается, что это число может разве лишь уменьшаться, и уменьшается на единицу тогда и только тогда, когда $ x_<> $ проходит через корень начального полинома системы, т.е. через корень $ f(x)_<> $.

Теорема [Штурм]. Если $ f(a)ne 0, f(b)ne 0 $, и система $ f_0(x), f_1(x),dots, f_K(x) $ является системой полиномов Штурма для $ f(x_<>) $, то

$$ operatorname $. Оказывается, что в качестве полиномов системы Штурма можно взять последовательность остатков из алгоритма Евклида, если только домножить некоторые из них на $ -1_<> $. Именно, возьмем $$f_1(x) equiv f'(x) .$$ Поделим $ f_<0>(x) equiv f(x) $ на $ f_<1>(x) $ и обозначим через $ f_<2>(x) $ остаток, домноженный на $ -1_<> $: $$f_0(x)equiv q_1(x) f_1(x)-f_2(x), quad deg f_2 ☞ ЗДЕСЬ

Левая полуплоскость: устойчивость

Полином $ f(z) $ с комплексными коэффициентами называется устойчивым, если все его корни удовлетворяют условию $ <mathfrak Re>(z) 0 $ необходимо и достаточно, чтобы были выполнены неравенства

$$ a_1>0, left| begin a_1 & a_3 \ a_0 & a_2 end right|>0, left| begin a_1 & a_3 & a_5\ a_0 & a_2 & a_4 \ 0 & a_1 & a_3 end right|>0,dots, left| begin a_1 & a_3 & a_5 & dots & 0\ a_0 & a_2 & a_4 & dots & 0 \ 0 & a_1 & a_3 & dots & 0 \ 0 & a_0 & a_2 & dots & 0 \ dots & & & ddots & dots \ dots & & & dots & a_n end right|>0 . $$

Единичный круг

Единичным кругом на комплексной плоскости назовем круг $ |z|le 1 $.

Задача. Найти необходимые и достаточные условия на коэффициенты полинома $ f(z)=a_0z^n+dots+ a_n $, при которых все его корни $ lambda_1,dots, lambda_n $ находятся внутри единичного круга, т.е. удовлетворяют условию $ |z| 0, A_1>0, A_2>0, A_3>0, A_1A_2-A_0A_3>0 ; $$ и $$A_0 0 .$$ Подставляя сюда выражения для коэффициентов, получим, что первая система ограничений имеет решение $ -1 |mbox < свободный член >f(z)| , $$ т.е. $ |a_0| > |a_n| $, и полином $$ f_1(z) = frac(z)> quad npu quad f^<*>(z) = z^nf(1/z) equiv a_0+a_1z+dots+a_nz^n $$ имеет все свои корни лежащими внутри единичного круга.

На первый взгляд, конструктивность этого результата не очень очевидна: исходная задача для полинома $ f(z) $ сводится к аналогичной задаче для полинома $ f_1(z) $. Обратим, однако, внимание на то, что полином $$ begin f_1(z)&=& left[a_0(a_0z^n+dots+a_n)-a_n (a_0+a_1z+dots+a_nz^n) right] big/ z = \ &=& left[(a_0^2-a_n^2)z^n+(a_0a_1-a_a_n)z^ + dots + (a_0a_-a_<1>a_n)z right] big/ z = \ &=& (a_0^2-a_n^2)z^+(a_0a_1-a_a_n)z^ + dots + (a_0a_-a_<1>a_n) end $$ имеет степень меньшую, чем $ deg f $. Таким образом, алгоритм конструктивен в том смысле, что он сводит исходную задачу к более простой. Применяя к полиному $ f_1(z) $ снова критерий Шура-Кона, получим следующее необходимое условие $$ |mbox < старший коэффициент >f_1(z) | > | mbox < свободный член >f_1(z)| iff quad |a_0^2-a_n^2| > |a_0a_-a_<1>a_n| , $$ при выполнении которого дальнейшему исследованию подлежит полином $$ f_2(z) = frac<(a_0^2-a_n^2)f_1(z)-(a_0a_-a_<1>a_n)f^<*>_1(z)> . $$ Продолжая процедуру, за конечное число шагов мы дойдем до полинома первой степени. Окончательно, необходимые и достаточные условия нахождения всех корней полинома $ f(z) $ степени $ n_<> $ внутри единичного круга получаются объединением $ n_<> $ условий $$ |mbox < старший коэффициент >f(z) |>|mbox < свободный член >f(z)| , $$ $$ |mbox < старший коэффициент >f_1(z) | > |mbox < свободный член >f_1(z)| , $$ $$ vdots qquad qquad qquad vdots $$ $$ |mbox < старший коэффициент >f_(z) |>|mbox < свободный член >f_(z)| . $$

Пример на применение этой теоремы ☞ ЗДЕСЬ.

Численные методы поиска корней полинома

Как упоминалось ☝ ВЫШЕ, корни полинома $ f_<>(z) $, как правило, не выражаются в радикалах уже при $ deg f=5 $ . Но даже в тех случаях, когда выражаются, как, например, $$lambda=frac<sqrt<5>-1 + sqrt<10- sqrt<20>>> <2>quad mbox < для > f(x)=x^4+2x^3-6x^2-2x+1 , $$ толку от такого представления мало: на каком интервале вещественной оси лежит $ lambda $? Поэтому наряду с поиском аналитических формул для корней полиномов практический интерес представляет нахождение их приближенных значений. Эту задачу будем решать, в основном, для полиномов над $ mathbb R_<> $ (т.е. полиномов с вещественными коэффициентами), с которыми чаще всего и приходится иметь дело на практике.

Нас, прежде всего, будут интересовать именно вещественные корни полиномов. В дальнейшем переменную этих полиномов будем обозначать через $ x_<> $ и считать ее вещественной. Для поиска вещественных корней полинома, как правило, требуется их предварительно отделить, т.е. найти интервалы $ ]a,b_<>[ $, каждый из которых содержит только один корень $ f_<>(x) $. Поиск такого интервала можно производить разными способами, самый общий из которых изложен ☝ ВЫШЕ. Однако, для предварительного понимания изложенных ниже методов, достаточно будет ориентироваться на теорему Больцано: полином имеет корень на $ ]a,b_<>[ $, если на концах интервала он принимает значения разных знаков. Этот корень будет единственным, если дополнительно предположить, что функция $ f_<>(x) $ монотонна на $ ]a,b_<>[ $. Последнее условие будет очевидно выполнено, если производная $ f^<prime>(x) $ не меняет знака на $ ]a,b_<>[ $, т.е. полином $ f^<prime>(x) $ не имеет корней на рассматриваемом интервале. Действительно, если предположить существование двух корней у $ f_<>(x) $ на $ ]a,b_<>[ $, то, по соображениям, упомянутым ☞ ЗДЕСЬ 16) , должна существовать точка этого интервала, в которой $ f^<prime>(x) $ обращается в нуль. Анализ знака $ f^<prime>(x) $ на $ ]a,b_<>[ $ часто удается произвести элементарными рассуждениями.

источники:

http://abakbot.ru/online-16/312-podbor

http://vmath.ru/vf5/polynomial

Пусть
на отрезке
в некоторой последовательностиузловзадана функциясвоими значениями,
где.
Задача алгебраического интерполирования
состоит в построении многочленастепени,
удовлетворяющего условию интерполирования:.

Известно,
что существует единственный полином
степени не выше
,
принимающий в исходных точках заданные
значения. Коэффициентыполиномаможно определить из системы уравнений:

Определитель
этой системы есть определитель
Вандермонда, и, следовательно, система
имеет единственное решение.

Пример.
Построить интерполяционный многочлен
,
совпадающий с функциейв точках.

Решение.
Пусть
,
поэтому имеем

.

Отсюда
.

Поэтому
при.

Многочлен Лагранжа

Будем
искать многочлен в виде линейной
комбинации множеств степени
:.

При
этом потребуем, чтобы каждый многочлен
во всех узлах интерполяции, за исключением
одного,
где он равен 1. Легко проверить, что этим
условиям отвечает многочлен вида

.

Действительно,
.
Причислитель выражения равен 0. По аналогии
получим:

,

.

Подставив эти
формулы в исходный многочлен, получим:

.

Эта формула
называется интерполяционным многочленом
Лагранжа.

Пример.
Построить интерполяционный многочлен
Лагранжа
,
совпадающий с функциейв точках

.

Решение.
Составим таблицу

х	-2	-4/3	0	4/3	2
у	0	1	2	1	0

Подставляя эти
значения в формулу Лагранжа, получим:

Если
функция
непрерывно дифференцируема до-го
порядка включительно, то остаточный
член интерполяционного многочлена в
форме Лагранжа имеет вид

,

где
– внутренняя точка минимального отрезка,
содержащего узлы интерполированияи точку.

Многочлен Ньютона с конечными разностями

Рассмотрим
случай равноотстоящих узлов интерполяции,
т. е.
– называется шагом.

Введем
понятие конечных разностей. Пусть
известны значения функции в узлах
.
Составим разности значений функции:

Эти разности
называются разностями первого порядка.

Можно составить
разности второго порядка:

.

Аналогично
составляются разности k-го
порядка:

.

Выразим
конечные разности непосредственно
через значение функции:

Таким
образом, для любого k
можно записать:

Запишем
эту формулу для значений разности в
узле
:

.

Используя конечные
разности, можно определить

.

Перейдем к построению
интерполяционного многочлена Ньютона.
Этот многочлен будем искать в виде

.

График
многочлена должен проходить через
заданные узлы, то есть
.
Используем эти условия для нахождения
коэффициентов многочлена:

Найдем
отсюда коэффициенты
:

Таким
образом, для любого
-го
коэффициента формула примет вид

.

Подставляя
эти формулы в выражение многочлена
Ньютона, получим его следующий вид:

Полученную
формулу можно записать в другом виде.
Для этого введем переменную
.

В этом
случае

С
учетом этих соотношений формулу
многочлена Ньютона можно записать в
виде

.

Полученное
выражение может аппроксимировать данную
функцию
на всем отрезке изменения аргумента.
Однако более целесообразно (с точки
зрения повышения точности расчетов и
уменьшения числа слагаемых в полученой
формуле) ограничиться случаем,
то есть использовать эту формулу для
всех.
Для других случаев вместопринять,
еслипри.
В этом случае интерполяционный многочлен
можно записать в виде

Полученная
формула называется первым интерполяционным
многочленом Ньютона для интерполяции
вперед. Эту интерполяционную формулу
обычно используют для вычисления
значений функции в точках левой половины
рассматриваемого отрезка. Это объясняется
следующим: разности
вычисляются через значения функции,
причем.
Из-за этого при больших значенияхмы не можем вычислить высших порядков.

Для
правой половины рассматриваемого
отрезка разности лучше вычислять справа
налево. В этом случае
,
то есть,
и интерполяционный многочлен Ньютона
можно получить в виде:

.

Полученная
формула называется вторым интерполяционным
многочленом назад.

Пример.
Используя интерполяционный полином
Ньютона, вычислить
,
где функциязадана таблицей

х	0	0,1	0,2	0,3	0,4	0,5
у	0	0,1002	0,2013	0,8045	0,4108	0,5211

Решение.
Составляем
таблицу конечных разностей.

х	у
0	0
		0,1002
0,1	0,1002		0,0009
		0,1011		0,0012
0,2	0,2013		0,0021		-0,0002
		0,1032		0,0010		0,0001
0,3	0,3045		0,0031		-0,0001
		0,1063		0,0009
0,4	0,4108		0,0040
		0,1103
0,5	0,5211

Для
вычисления
положим в интерполяционном многочлене
Ньютона впередтогдаи

Пример.
Задана таблица. Найти
.

х
	0,2588
		0,0832
	0,3420		-0,026
		0,0806		0,0006
	0,4226		-0,032
		0,0774		0,0006
	0,5		0,038
		0,0736
	0,5736

При
вычислении
положим

.

При
вычислении
положим

.

Оценим погрешности
формул Ньютона вперед и назад:

где
и

где
.

Формулы
приближенного дифференцирования
основаны на первой интерполяционной
формуле Ньютона. Интерполяционный
многочлен Ньютона имеет вид

,

где

Производя
перемножение биномов, получим

так
как
,
то

.

Аналогично
можно вычислять производные функции
любого порядка.

В
некоторых случаях требуется находить
производные функций
в основных табличных точках.
Так как табличное значение можно считать
за начальное, то положив,
имеем

,

Для
производной многочлена Ньютона первого
порядка погрешность может быть вычислена
по формуле
,

где
– число конечных разностей в многочлене
Ньютона.

Пример.
Найти
функции,
заданной таблично.

Решение.

х	у
50	1,6990
		0,0414
55	1,7404		-0,0036
		0,0378		0,0005
60	1,7782		-0,0031
		0,0347
65	1,8129

Здесь
;.

Вычисляя погрешность,
получим:

.

Действительно,
.

Таким образом,
результаты совпадают до четвертого
знака.

Соседние файлы в папке ПРАКТИЧЕСКИЕ ЗАДАНИЯ

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Приближение многочленом с условием прохождения через точки

При моделировании данных методом наименьших квадратов, кривая обычно не проходит через точки измерений (рис. 1).

Что, если нужно, чтобы эта кривая точно проходила через одну или несколько особо выделенных точек (рис. 2 — показаны зелёными кружочками)?

Тогда читаем дальше.

1. Мотивация

Рассмотрим обычную задачу приближения многочленом и посмотрим, чего нам в ней не хватает.

Дано N точек на плоскости (x_i,y_i) — значения неизвестной функции f(x). Требуется найти многочлен p(x) степени M (M<N), наилучшим образом приближающий эту функцию.

Часто полагают, что «наилучшим» является многочлен, сумма квадратов отклонений которого от заданных точек минимальна:

В таком виде задача решается широко известным методом наименьших квадратов (МНК).

При M<N-1 многочлен p(x), вообще говоря, не проходит через все заданные точки (x_i, y_i) (рис. 1). Более того, часто оказывается, что он не проходит ни через одну из них.

Само по себе это не плохо. Обычно данные, по которым строится приближение, содержат погрешности измерений. Даже лучше, что многочлен не проходит через все точки, так как при этом ошибки измерений сглаживаются.

Однако бывает, что о моделируемой зависимости имеются дополнительные сведения. Например, моделируется отклик датчика на некую величину. И из физических соображений ясно, что этот отклик строго равен нулю при равенстве нулю величины. При моделировании характеристики такого датчика может оказаться, что аппроксимирующий многочлен не пройдет через нуль. В результате модель даст большую погрешность в районе нуля.

В такой ситуации хотелось бы найти многочлен со следующими свойствами:

1. Точно проходит через нуль

2. Имеет наименьшую сумму квадратов отклонений от остальных измеренных значений

В статье описывается метод, позволяющий найти такой многочлен. Более того, можно потребовать точного прохождения многочлена не через одну, а несколько выделенных точек.

2. Решение

2.1. Взвешенный метод наименьших квадратов

Как ингредиент нам потребуется взвешенный метод наименьших квадратов, который минимизирует сумму квадратов отклонений с весовыми коэффициентами в каждой точке:

Где w_i — весовые коэффициенты. Обычно взвешенный МНК используется для учета погрешностей измерений в каждой точке, поэтому в литературе часто используют не понятие веса, а обратную дисперсию σ² погрешностей:

Взвешенный МНК хорошо описан в книге [1], гл. 15.1, 15.4.

2.2. Точное прохождение через нуль

Начнём с простого случая: потребуем точного прохождения многочлена p(x) через нуль.

Для этого найдём многочлен q(x) степени M-1 по модифицированным точкам (x_i, y_i/x_i) с помощью взвешеннго МНК, выбрав в качестве весов w_i=x_i²; и умножим его на x. Тогда:

Он будет иметь степень M и точно проходить через нуль.

Рассмотрим сумму квадратов его отклонений от остальных точек (x_i, y_i):

Но именно эта величина и минимизируется взвешенным МНК по модифицированным точкам. Поэтому многочлен p(x) будет соответствовать и второму условию задачи — иметь наименьшую сумму квадратов отклонений от (x_i, y_i).

2.3. Точное прохождение через одну произвольную точку

Усложним задачу и потребуем точного прохождения многочлена p(x) через одну произвольно заданную точку (ξ,η).

Путём замены переменных u=x-ξ, v=y-η, задача сводится к рассмотренной выше. Находим коэффициенты многочлена p₀(u), проходящего через нуль и имеющего наименьшую сумму квадратов отклонений p₀(u_i)-v_i. Далее переходим к исходным переменным:

Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с коэффициентами p₀(x-ξ), но есть и более простой на практике способ. Поскольку у нас в программе уже имеется реализация обычного МНК, то можно просто вычислить значения p(x) по формуле (1) в каких-нибудь M+1 или более точках, и применить к этим значениям обычный МНК, задав степень многочлена M. Тем самым и будут найдены коэффициенты p(x).

2.4. Точное прохождение через несколько точек

И, наконец, самый общий случай — потребуем точного прохождения многочлена p(x) через K заданных точек (ξ_i, η_i). Следует выбирать K ≤ M, в противном случае задача вырождается в интерполяцию.

Переходя к решению, введем многочлен z(x) степени K:

Он имеет нули в точках ξ₁, ξ₂, … ξ_K.

Также введем интерполяционный многочлен Лагранжа L(x) степени K-1, проходящий через точки (ξ_i, η_i) [1], гл. 3.1.

Используем взвешенный МНК для нахождения многочлена q(x) степени M-K по модифицированным точкам: (x_i, (y_i-L(x_i))/z(x_i)) с весовыми коэффициентами w_i=z(x_i)². Получим коэффициенты {a_j} для q(x), которые минимизируют сумму:

Теперь составим многочлен p(x) как:

Докажем, что p(x) является решением задачи.

1. Прохождение через точки (ξ_i, η_i) обеспечивается тем, что z(ξ_i)=0, обращая в нуль первое слагаемое. Второе слагаемое в этих же точках, L(x), проходит через (ξ_i, η_i) по построению.

2. Степень p(x) равна M, так как степень произведения многочленов q(x) и z(x) равна сумме степеней множителей. В данном случае M-K+K=M. Сумма же многочленов имеет степень старшего из слагаемых. Степень L(x) равна K-1, что по условию меньше M.

3. Запишем сумму квадратов отклонений в точках (x_i, y_i):

Но это совпадает с величиной (2), которая минимизировалась при нахождении коэффициентов q(x). Следовательно, p(x_i) имеет наименьшую сумму квадратов отклонений от y_i. Что и требовалось доказать.

Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с q(x), z(x) и L(x), но это еще сложнее, чем в разделе 2.3. выше. Так что здесь тоже рекомендуется вычислить значения p(x) в M+1 или более точках по формуле (3) и применить к ним обычный МНК.

3. Цена вопроса и рекомендации к применению

За всё в этой жизни приходится платить. Наложение условия точного прохождения через точки (ξ_i, η_i) на многочлен p(x) приводит к тому, что сумма квадратов его отклонений от остальных точек (x_i, y_i) оказывается, вообще говоря, выше, чем без наложения условий.

Фактически, мы решили задачу условной оптимизации суммы квадратов отклонений p(x_i)-y_i. Как и в других задачах условной оптимизации, достигаемое значение целевой функции получается хуже, чем при оптимизации безусловной. В противном случае и безусловная оптимизация дала бы тот же результат.

Когда же следует применять описанный метод? Тогда, когда о моделируемой зависимости имеются «железобетонные» сведения, что она должна проходить через точки (ξ_i, η_i) независимо от экспериментальных данных (x_i, y_i).

В моей практике был один такой случай. Моделировалась нелинейная характеристика датчика. Истинный вид функциональной зависимости был неизвестен. Оставалось только использовать многочлены в попытке хоть как-то компенсировать нелинейность. Но многочлены плохо описывали характеристику около нуля. Полученные обычным МНК, они стремились не проходить через нуль. Тем не менее, из физических соображений было ясно, что характеристика датчика должна проходить через нуль. Вот тогда наложение условия и пригодилось. Его применение позволило улучшить компенсацию нелинейности в окрестностях нуля и уменьшить относительную погрешность прибора в целом.

4. Пример с конкретными числами

Этот пример был использован для построения графиков, приведенных на рис. 1 и рис. 2.

В качестве «истинной зависимости» был взят следующий многочлен:

Где T₃(x) — многочлен Чебышева третьего порядка. Модификации применены к нему для того, чтобы отобразить интересный участок графика в диапазон x,y ∈ [0; 1]. p₁(x) проходит через точки (0,0) и (1,1). Разложение его по степеням x выглядит так:

В качестве данных для метода наименьших квадратов (обычного и условного) взяты значения p₁(x) в 11 равноотстоящих точках между 0 и 1 с шагом в 0,1. К значениям многочлена была добавлена нормально распределенная «ошибка измерений» δ_i с дисперсией σ²=0,04. В точках x₁=0 и x₁₁=1 ошибка не добавлялась. По случайным числам карты легли следующим образом:

Приближение обычным МНК по заданным точкам при M=3 дало следующие коэффициенты:

График p₂(x) изображен на рис. 1. Достигнутая сумма квадратов отклонений p₂(x)-y_i составила 0,4019.

Для испытания описываемого в разд. 2.4. метода было поставлено условие точного прохождения многочлена через точки (0,0) и (1,1), а в остальных точках — минимизация суммы квадратов отклонений. В результате был получен следующий многочлен:

Его график изображен на рис. 2. Достигнутая сумма квадратов отклонений p₃(x)-y_i составила 0,5046.

Из приведенного примера можно сделать вывод, что теоретические выкладки подтвердились. Был найден многочлен p₃(x), приближающий «экспериментальные данные» и проходящий через точки (0,0) и (1,1). Как предсказывалось в разд. 3, сумма квадратов его отклонений от точек (x_i, y_i) оказалась больше, чем у многочлена p₂(x), найденного обычным МНК. Тем не менее, эта жертва может быть оправданной, если прохождение p₃(x) через точки (0,0) и (1,1) важнее.

Что касается совпадения коэффициентов многочленов p₂(x) и p₃(x) с коэффициентами «истинного» многочлена p₁(x) — то на паре-тройке наборов тестовых данных особой закономерности не выявилось. Наверное, есть смысл провести тест Монте-Карло и сравнить распределения коэффициентов p₂(x) и p₃(x) на большой выборке.

Заключение

В статье был получено обобщение метода наименьших квадратов, позволяющее налагать на многочлен условие прохождения через заданные точки.

Задачу удалось свести к применению взвешенного метода наименьших квадратов и интерполяции многочленом Лагранжа. Поскольку обе операции сводятся к решению системы линейных уравнений, то и описанный в статье метод сохраняет эту (невысокую) вычислительную сложность. Точное решение можно получить за конечное число действий и (при должной усидчивости или использовании систем компьютерной алгебры) выразить аналитически.

Возможны обобщения метода для задач приближения не только многочленами, а и другими функциями. Но эта тема обширна и может быть рассмотрена только в отдельных публикациях.

Литература

[1] William H. Press и др. «Numerical Recipes in C++: The Art of Scientific Computing», Second Edition. Cambridge University Press, ISBN 0-521-75033-4

Рассмотрим построение полинома n-й степени в Matlab на примере следующей задачи.

Задача 1.
Найти приближенное значение функции при заданных значениях аргумента с помощью
интерполяционных полиномов n-й
степени в точках x1=0,702,  x2=0,512,
x3=0,608.
Функция задана таблично с постоянным шагом:

x	0.45	0.5	0.55	0.6	0.65	0.7	0.75
y	1.63597	1.73234	1.87686	2.01345	2.15455	2.22846	2.35973

В
Matlab
отсутствуют встроенные функции для построения интерполяционного полинома n-й степени, однако средств пакета
достаточно для написаний функций, реализующих полином. Ниже представлена
функция на М-языке для вычисления в точке t по экспериментальным значениям (xi,yi,i=1,2,…,n) значения:

·       
канонического полинома;

·       
полинома Ньютона;

·       
полинома Лагранжа.

1)   
Вычисление значения канонического полинома

Function s=kanon(x, y, t)

%
вычисление количества точек в массивах x и y

n=length (x);

%
формирование коэффициентов системы уравнений :

For i=1:n

For j=1:n

A(i,j)=x(i).^(j-1);

End

End

%
Решение системы уравнений :

a=A^(-1)*y;

%
вычисление значения канонического полинома по формуле :

S=0;

For i=1:n

S=s+a(i)*t^(i-1);

End

End

2)   
Вычисление значений полинома Ньютона

Function s = newton(x,y,t)

% Вычисление количества точек в массивах x и y для полинома Ньютона:

N=length (x)

%
запись в первый столбец матрицы разделенных разностей вектора y :

For i=1:n

C (i,1) = y (i);

End

%
формирование матрицы разделенных разностей :

For i=2:n

For j=2:n

If (i<j)

C(i ,j) = 0

Else

C(i ,j) = (C(i ,j-1)-C(j-1, j-1)) / (x(i)-x(j-1));

End

End

End

%
формирование массива коэффициентов полинома Ньютона :

For i=1:n

A(i)= C(i ,j);

End

%
расчет значения полинома Ньютона в точке t по формуле :

S=0;

For i=1:n

P=1;

For j=1:i-1

P=p*(t-x(j));

End

S=s+A(i)*p;

End

End

3)   
Вычисление значения полинома Лагранжа

Function s=lagrang (x, y, t)

%
вычисление количества точек в массивах x и y

n=length (x);

S=0;

%
расчет суммы произведений по формуле

%
для вычисления значения полинома Лагранжа в точке t

For i=1:n

P=1;

For j=1:n

If (j~=i)

P=p*(t-x(j))/(x(i)-x(j));

End

End

S=s*y(i)*p;

End

End

Для
вычисления значения функции в точках x1=0,702,
x2=0,512,
x3=0,608
необходимо сформировать массив r=(0,702*0,512*0,608)
и в цикле обратиться к одной из приведенных в программах функций. Далее в
программе показано обращение к функции lagrang(так же можно
обратиться к функциям kanon
и newton)
для вычисления значения полинома в точках x1=0,702, x2=0,512, x3=0,608.

r=[0.702 0.512 0.608]

r=

0.7020  
0.5120   0.6080

for i=1:3

rs(i)=lagrange (x, y, r(i));

end

rs

rs=

2.2336   1.7970 
2.0057