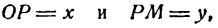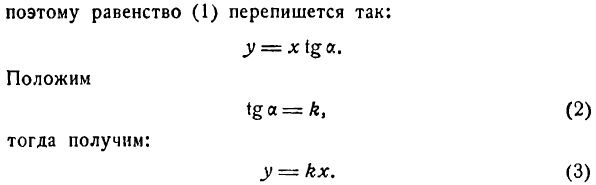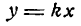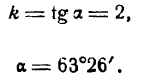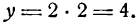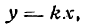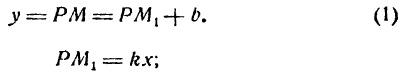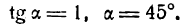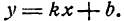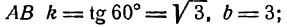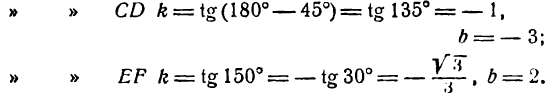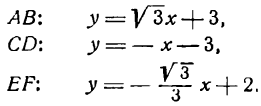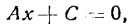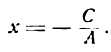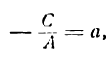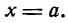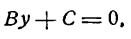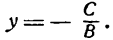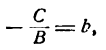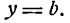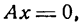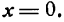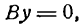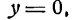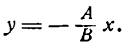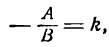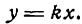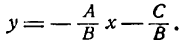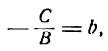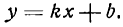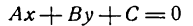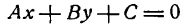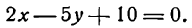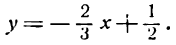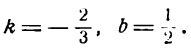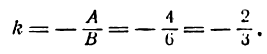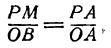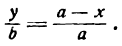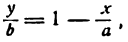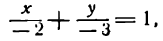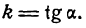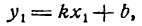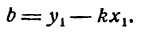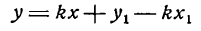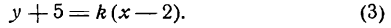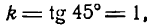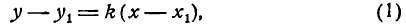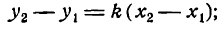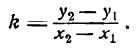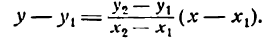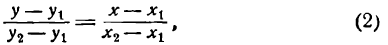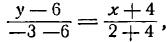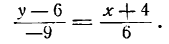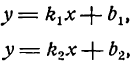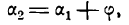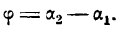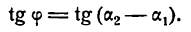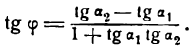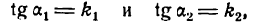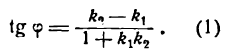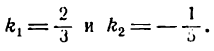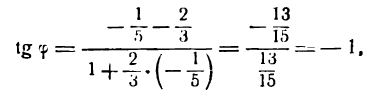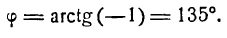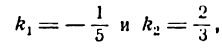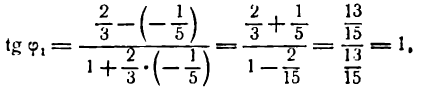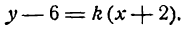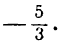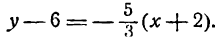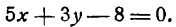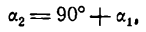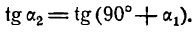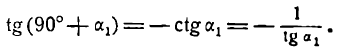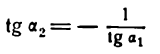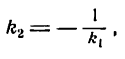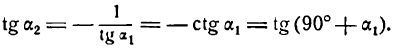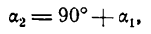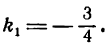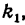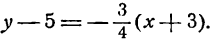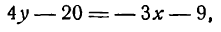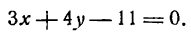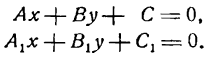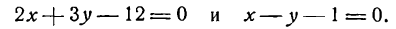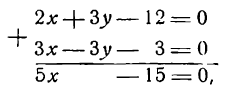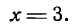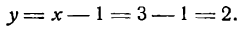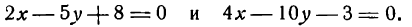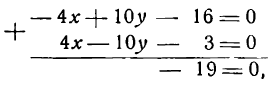Как найти уравнение прямой а1а2

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).

Уравнения прямых, параллельных осям координат

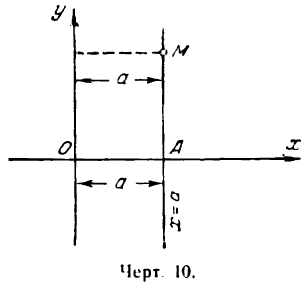
Возьмем прямую линию, параллельную оси Оу и проходящую на расстоянии а от нее (рис. 10).

Все точки этой прямой одинаково удалены от оси ординат на расстояние, равное а. Следовательно, для каждой точки прямой АМ абсцисса одна и та же, а именно:

х = а, (1)

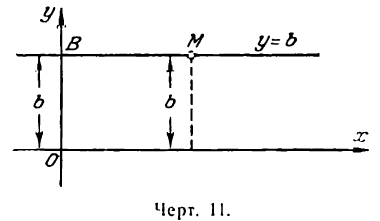
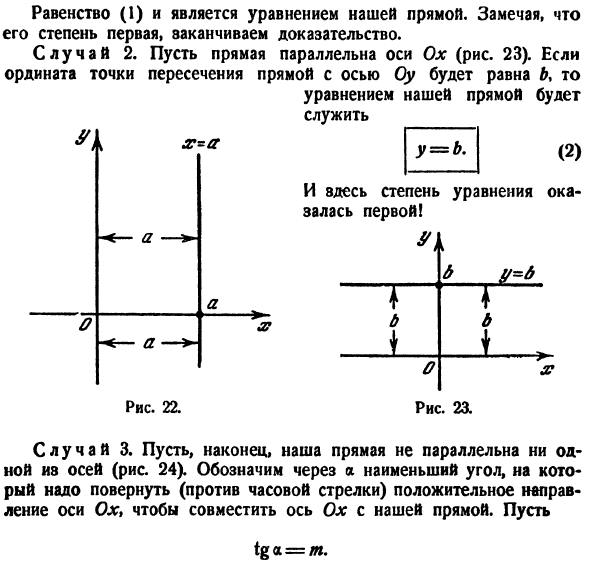
ордината же различна. Таким образом, уравнение (1) вполне определяет прямую, параллельную оси Оу, а потому оно является ее уравнением. Возьмем прямую, параллельную оси Ох, на расстоянии.

равном b от нее (рис. 11). Все точки этой прямой одинаково удалены от оси Ох на расстояние, равное b , т. е. любая точка прямой ВМ имеет постоянную ординату, а именно:

абсциссу же различную. Как видно, уравнение (2) вполне определяет прямую, параллельную оси Ох, а потому оно является ее уравнением.

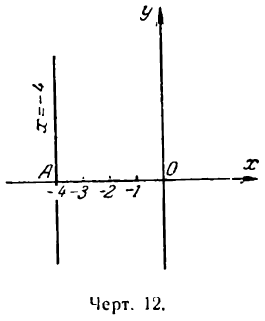
По уравнениям (1) и (2) можно построить соответствующие им прямые. Пусть, например, дана прямая х = — 4. Отложив на оси Ох отрезок ОА = — 4 (рис. 12) и проведя через точку А прямую, параллельную оси Оу, получим искомую прямую.

Уравнения осей координат

Возьмем уравнение прямой, параллельной оси Оу:

х = а

и станем в нем уменьшать абсолютную величину а, тогда прямая, определяемая этим уравнением, будет приближаться к оси Оу, оставаясь все время ей параллельной, и при а = 0 сольется с ней. Уравнение х = 0 является уравнением оси Оу.

Если же в уравнении у = b прямой, параллельной оси Ох, будем уменьшать абсолютную величину b то эта прямая станет приближаться к оси Ох, оставаясь ей параллельной, и при b = 0 с ней совпадет. Таким образом, уравнение у = 0 будет уравнением оси Ох.

Уравнение прямой, проходящей через начало координат

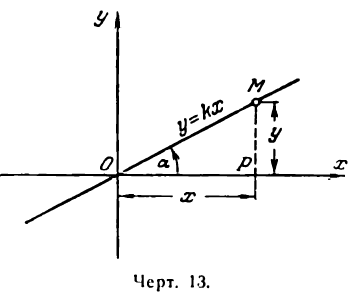
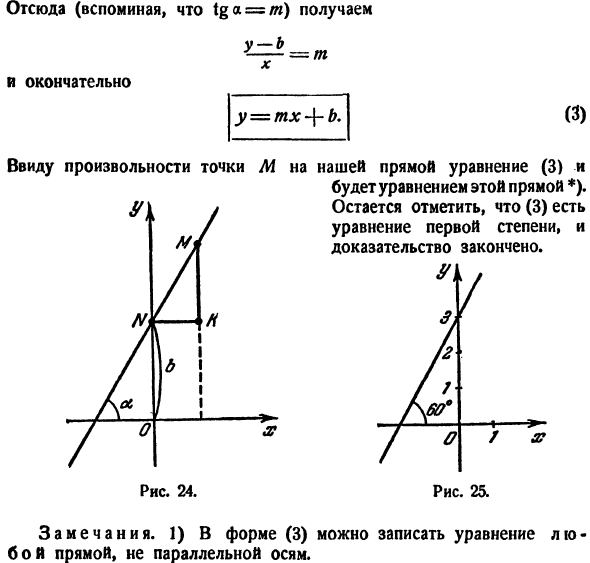
Проведем прямую через начало координат под углом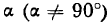

к оси Ох (рис. 13). Принято положительный угол а отсчитывать от положительного направления оси абсцисс в сторону, противоположную движению часовой стрелки (рис. 13), а отрицательный — по часовой стрелке.

Возьмем на проведенной прямой произвольную точку М (х; у). Опустив перпендикуляр МР на ось Ох, получим прямоугольный треугольник ОМР, из которого найдем:

Но

Координаты любой точки прямой ОМ удовлетворяют полученному уравнению; можно показать, что координаты любой точки, не лежащей на прямой ОМ, не удовлетворяют ему; поэтому оно является уравнением прямой ОМ. Итак,

есть уравнение прямой, проходящей через начало координат. В нем х и у — текущие координаты, а — угловой коэффициент.

Определение:

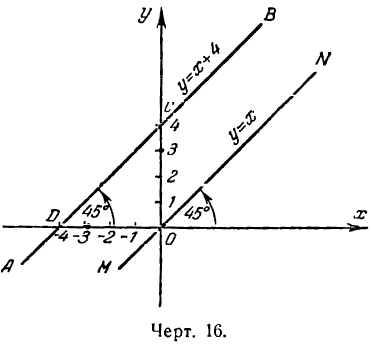
Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к положительному направлению оси Ох.

Величина может быть как положительной, так и отрицательной. Если угол а острый, то тангенс его имеет положительное значение; если же угол а тупой, —то отрицательное. Поэтому величина в уравнении прямой будет положительной, если а — острый угол, и отрицательной, если тупой.

Заметим, что при а = 90° углового коэффициента не существует, так как 90° не имеет числового значения.

Зная угловой коэффициент прямой у = х, можно определить ее положение.

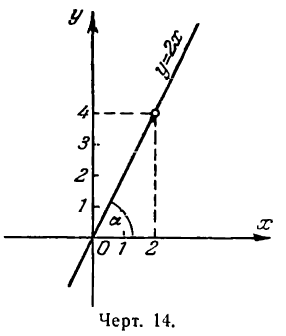
Пусть требуется построить прямую у= 2х.

Для этого найдем угол а из условия

откуда:

Построив при точке О найденный угол, мы и получим искомую прямую (рис. 14).

Построение этой прямой можно провести и проще.

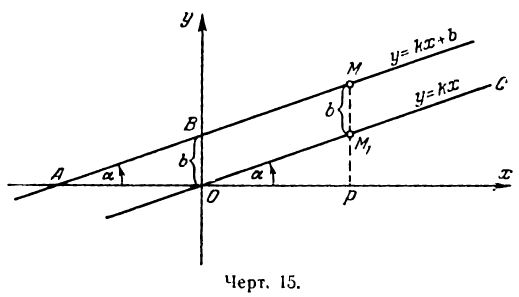
Известно, что положение прямой определяется двумя точками, поэтому для решения задачи нужно знать их координаты. В нашем же случае достаточно определить координаты одной точки, так как вторая (начало координат) нам известна. Для этого дадим х произвольное значение, например х = 2, тогда из уравнения прямой найдем:

Значения х = 2 и у = 4 и будут координатами точки, лежащей на данной прямой. Построив эту точку, проведем через нее и начало координат прямую линию (рис. 14).

Уравнение прямой с угловым коэффициентом и начальной ординатой

Пусть дана прямая ОС, проходящая через начало координат под углом а к положительному направлению оси Ох (рис. 15)

Ее уравнение имеет вид

где .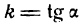

Проведем прямую 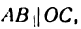отсекающую на оси Оу отрезок ОВ = b. Прямая АВ составляет с положительным направлением оси Ох тот же угол а. Пусть М(х; у)— произвольная точка прямой АВ. Из рис. 15 найдем:

Но

Подставив значение РМ1 в равенство (1), получим уравнение прямой АВ в виде:

где — угловой коэффициент, а b называется начальной ординатой.

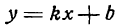
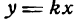
Заметим что прямая получается смещением всех точек прямой (рис. 15) на отрезок b вверх (при положительном b) и вниз при отрицательном b .

Уравнение 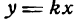определяющее прямую проходящую через начало координат, является частным случаем уравнения (2) при b = 0.

Зная угловой коэффициент и начальную ординату b можно определить положение прямой. Пусть, например, требуется построить прямую

Из данного уравнения имеем:

откуда

Проведем через начало координат прямую МN под углом в 45 градусов к положительному направлению оси Ох (рис. 16). На прямую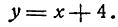

Как видно из уравнения ее пересекает ось Оу на расстоянии ОС, равном 4 единицам масштаба от начала координат.

Поэтому прямая АВ, проведенная через точку С параллельно прямой МN, и будет искомой.

Однако проще построить указанную прямую по двум ее точкам. Удобнее для этого брать точки пересечения прямой с осями координат. Одна из них — точка С пересечения прямой с осью Оу— дается самим уравнением, а именно С(0; 4). Для нахождения точки D пересечения этой прямой с осью Ох положим в данном уравнении y = 0, получим х = — 4; значит, прямая пересекает ось Ох в точке D (-4; 0). Строим точки С и D и проводим через них искомую прямую.

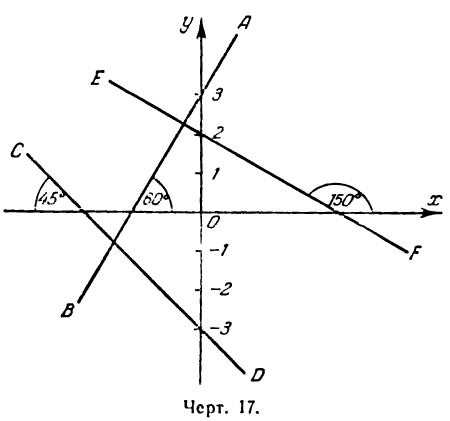
Пример:

Найти уравнения прямых АВ, СD и ЕF, изображенных на рис. 17.

Решение:

Чтобы написать уравнения данных прямых, нужно определить величины и b, а затем подставить их значения в уравнение

Для прямой АВ

Следовательно, уравнения данных прямых будут:

Общее уравнение прямой

В предыдущей лекции были выведены следующие виды уравнения прямой: уравнение прямой, параллельной оси Оу:

уравнение прямой, параллельной оси Ох:

уравнение оси Оу:

уравнение оси Ох:

уравнение прямой, проходящей через начало координат:

уравнение прямой с угловым коэффициентом и начальной ординатой:

Уравнения (1) — (6) исчерпывают все возможные положения прямой, поэтому можно сказать, что

всякая прямая линия определяется уравнением первой степени относительно текущих координат.

Покажем теперь, что указанные виды уравнения прямой можно получить из уравнения

при некоторых частных значениях коэффициентов А, В и С.

I. Если В = 0, то уравнение (7) обратится в следующее:

откуда

Положив

получим

Уравнение 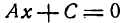есть уравнение прямой, параллельной оси Оу.

II. Если А = 0, то

отсюда

Положив

получим

Уравнение 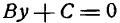определяет прямую, параллельную оси Ох.

III. Если В = 0 и С = 0, то

отсюда

IV. Если А = 0 и С = 0, то

отсюда

V. Если С = 0, то

отсюда

Положим

тогда

Уравнение 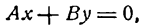определяет прямую, проходящую через начало координат.

VI. Если ни один из коэффициентов уравнения (7) не равен нулю, то и в этом случае его можно преобразовать в знакомую нам форму уравнения прямой. Найдем из уравнения (7) значение у:

Положив

и

можем написать

Следовательно, уравнение

включает в себя все рассмотренные нами ранее уравнения прямой; поэтому оно называется общим уравнением прямой. Итак, всякое уравнение первой степени

при любых значениях коэффициентов А, В и С, исключая одновременное равенство А и В нулю, определяет прямую линию.

Пример:

Построить прямую

Решение:

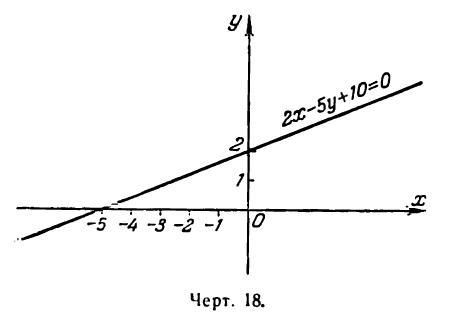
Проще всего построить прямую по двум ее точкам пересечения с осями координат. Положив в данном уравнении у = 0, получим х =- 5; координаты (-5; 0) и будут определять положение точки пересечения прямой с осью Ох. Для нахождения точки пересечения прямой с осью Оу положим в том же уравнении х = 0 тогда найдем у = 2; координаты искомой точки будут (0; 2).

Построив эти точки, проводим через них прямую 2х— 5у —10 = 0 (рис. 18).

Пример:

Найти угловой коэффициент и начальную ординату прямой 4х+ 6у — 3 = 0.

Решение:

Преобразуем это уравнение к виду

для этого находим:

6у = — 4х + 3,

отсюда

Сравнив полученное уравнение с уравнением 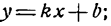найдем:

Угловой коэффициент можно найти и из равенства (8). Для этого, как видно, нужно коэффициент при х общего уравнения прямой разделить на коэффициент при у и частное

взять с противоположным знаком. Таким образом, в данном примере

Уравнение прямой в отрезках

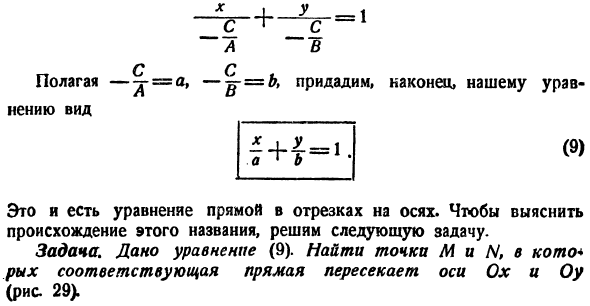
Как мы уже знаем, положение прямой определяется или двумя точками или одной точкой и углом наклона прямой к оси Ох. Если прямая не параллельна ни одной из координатных осей и не проходит

через начало координат, то ее положение может быть определено и другими данными, например отрезками, которые она отсекает на осях. Выведем уравнение прямой для этого случая.

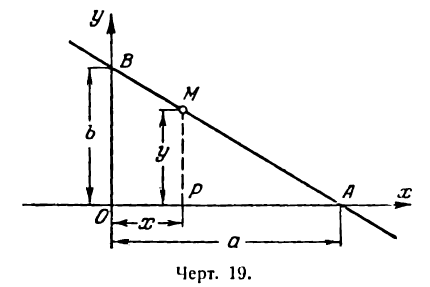
Пусть дана прямая, отсекающая на координатных осях отрезки ОА = а и ОВ = b (рис. 19).

Возьмем на этой прямой произвольную точку M (х; у) и проведем

МР 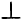Ох. Из подобия треугольников РМА и ОВА имеем:

или

Разделив а — х почленно на а, будем иметь:

откуда

Можно показать, что координаты любой точки нашей прямой будут удовлетворять этому равенству, а потому его нужно рассматривать как уравнение прямой АВ.

В уравнение (1) входят отрезки а и b , отсекаемые прямой на осях; поэтому оно называется уравнением прямой в отрезках.

Величины а и b могут быть как положительными, так и отрицательными в зависимости от того, в какую сторону от начала координат откладываются отрезки а и b .

Пусть, например, дана прямая АВ (рис. 20). Здесь а = — 2, b = — 3; следовательно, уравнение прямой АВ запишется в таком виде:

По уравнению вида (1) Очень просто строится прямая. Для этого нужно только отложить на осях отрезки а и b взятые из уравнения, и через их концы провести прямую.

Заметим, что уравнение в отрезках легко получается из общего уравнения прямой: Ах + Ву + С= 0, если все коэффициенты общего уравнения отличны от нуля (иначе уравнение в отрезках не имеет смысла).

Уравнение пучка прямых

Пусть прямая АВ проходит через точку М(х1; у1) и образует угол а с положительным направлением оси Ох (рис. 21). Составим для прямой АВ уравнение вида

Для этого нужно найти величины и b определяющие прямую АВ, а затем подставить в уравнение (1) их значения. Так как угол а дан, то величина определится из равенства

Для нахождения b воспользуемся тем, что точка М лежит на прямой (1) и, следовательно, ее координаты удовлетворяют уравнению этой прямой.

Подставив в уравнение (1) вместо х и у их значения х1 и у1, а величину полагая известной, получим

откуда

Уравнение (1) можем теперь записать в виде

или

Таково искомое уравнение прямой АВ; в нем имеет одно, вполне определенное значение.

Допустим, что через ту же точку M(х1; у1) проходит несколько прямых; тогда угол а наклона этих прямых к оси Ох, и также множитель в уравнении (2) будут иметь различные значения.

В таком случае уравнение (2) будет определять уже не одну прямую, проходящую через данную точку M, а множество прямых, пересекающихся в эточке.

Совокупность всех прямых, проходящих через одну точку М, называется пучком прямых с центром в точке М. Таким образом, уравнение (2) с переменным можно рассматривать как уравнение пучка прямых, проходящих через данную точку, исключая прямую, параллельную оси ординат (так как tg 90° не имеет числового значения) (рис. 21).

Чтобы выделить из этого пучка прямую, образующую заданный угол с осью Ох, нужно в уравнении (2) вместо подставить его числовое значение. Пусть, например, пучок прямых проходит через точку М(2;—5), тогда его уравнение будет:

Выделим из этого пучка одну прямую, которая наклонена к положительному направлению оси Ох под углом а = 45°;

тогда

и уравнение (3) обратится в следующее:

или

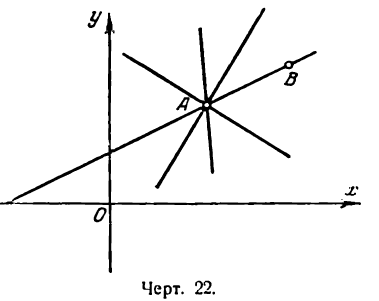
Уравнение прямой, проходящей через две данные точки

Пусть даны две точки A(х1; у1) и В(х2; у2); требуется найти уравнение прямой, проходящей через эти точки.

Если взять одну точку, например А, то через нее можно провести пучок прямых, уравнение которого будет:

где каждому значению отвечает одна прямая.

Выделим из этого пучка прямую, которая проходит и через вторую точку В (рис. 22). Чтобы найти ее уравнение, необходимо определить угловой коэффициент. Для этого примем во внимание, что точка В лежит на искомой прямой, и потому ее координаты должны обращать уравнение (1)

в тождество при равном угловому коэффициенту этой прямой. Подставив в уравнение (1) вместо текущих координат х и у координаты точки В, получим:

отсюда находим угловой коэффициент искомой прямой:

Уравнение (1) можно переписать так:

Преобразуем это уравнение, разделив обе части его на у2 — у1 получим:

гле х и у — текущие координаты. Равенство (2) является уравнением прямой, проходящей через две данные точки. Это, как и уравнение в отрезках, частный случай общего уравнения прямой.

Если х1 = х2 или у1 = у2, то формула (2) теряет смысл, так как делить на нуль нельзя. В этих случаях точки А и В лежат либо на прямой, параллельной оси Оу, либо на прямой, параллельной оси Ох. В первом случае уравнение прямой запишется в виде

х = х1

а во втором — в виде

у = у1

Пример:

Написать уравнение прямой, проходящей через две точки: А(—4; 6) и В(2; —3).

Решение:

Имеем:

х1 = —- 4, х2 = 2

и

у1 = 6, у2 = — 3.

Подставим эти значения в уравнение (2); получим:

или

Умножив обе части последнего уравнения на —18, будем иметь:

2у— 12 = — 3х— 12,

откуда

Зх + 2у = 0.

Пример:

Через две точки А( 3; 2) и В (5; 2) проходит прямая. Написать ее уравнение.

Решение:

Так как ординаты данных точек равны, то заключаем, что искомая прямая параллельна оси Ох, а потому ее уравнение будет

у = 2.

Угол между двумя прямыми

Пусть даны уравнения двух прямых:

y=klx+blt

где 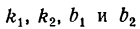имеют вполне определенные значения. Выведем формулу для определения угла между этими прямыми.

Обозначим углы, образуемые данными прямыми с положительным направлением оси Ох, через а1 и а2, а угол между этими прямыми через 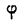(рис. 23).

Угол а2, как внешний угол треугольника ABC, будет равен сумме внутренних, с ним не смежных, т. е.

откуда

Если углы равны между собой, то и тангенсы их равны друг другу, поэтому

Применяя формулу для тангенса разности двух углов, получим:

Но

Поэтому

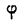
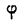
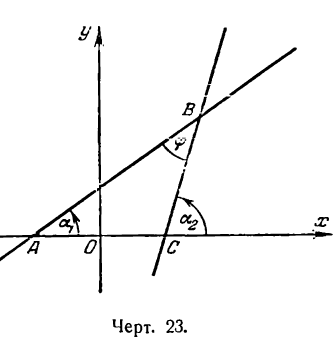
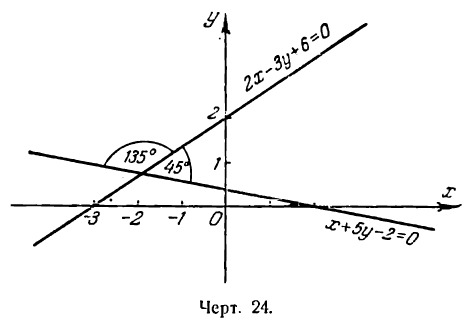
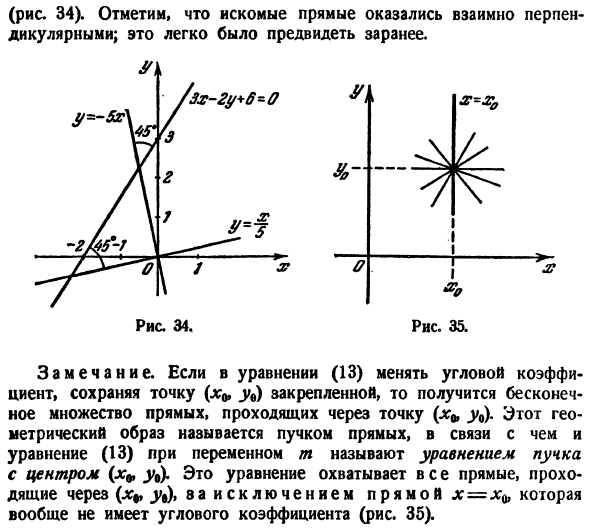
Определив tg по формуле (1), можно найти и самый угол .

Пример:

Определить угол между прямыми:

2х — 3у + 6 =0

и

х + 5у — 2=0.

Решение:

Из данных уравнений найдем угловые коэффициенты этих прямых :

Согласно формуле (1) имеем:

откуда

Полученный угол между прямыми тупой. Но если принять

то вычисляя 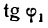по той же формуле (1), получим:

откуда 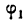= 45°. Получился угол острый, смежный с ранее

найденным тупым углом (рис. 24). Первое и второе значение угла будет ответом на вопрос задачи.

Условие параллельности прямых

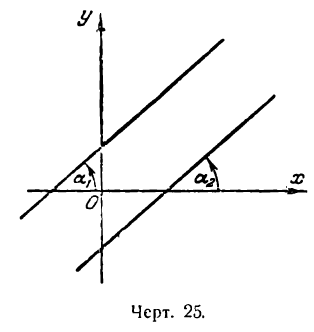
Если прямые параллельны между собой, то они образуют одинаковые углы а1 и а2 с положительным направлением оси Ох (рис. 25).

Из равенства углов а1 и а2 следует

или

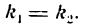
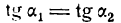
Обратно, если т.е. то а1 = а2, а это значит, что данные прямые параллельны.

Итак, если прямые параллельны между собой, то их угловые коэффициенты равны (и наоборот).

Пример:

Написать уравнение прямой, проходящей через точку А (—2; 6) и параллельной прямой 5х—3у — 7 = 0.

Решение:

Через точку А проходит пучок прямых, среди которых находится искомая прямая. Следовательно, прежде всего пишем уравнение пучка прямых , проходящих через точку А:

Затем находим из данного в задаче уравнения прямой ее угловой коэффициент; применяя равенство (8) , получим:

Согласно условию параллельности угловой коэффициент искомой прямой тоже равен

Подставим найденное значение 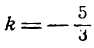в уравнение

пучка:

Выполнив необходимые преобразования, получим искомое уравнение прямой:

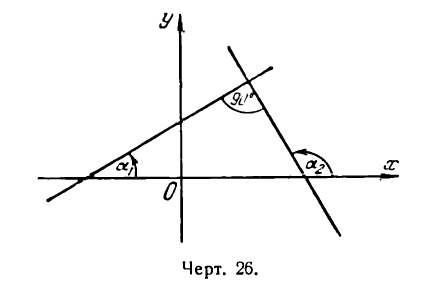
Условие перпендикулярности прямых

Пусть две прямые взаимно перпендикулярны и образуют с положительным направлением оси Ох углы а1 и а2 (рис. 26). В этом случае

отсюда

Но

Следовательно,

или

Обратно, если

то

Отсюда

т. е. данные прямые взаимно перпендикулярны.

Таким образом, если прямые взаимно перпендикулярны, то их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку (и наоборот).

Так, например, если у одной прямой угловой коэффициент

равен то у перпендикулярной ей прямой он равен .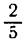

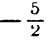
Пример:

Написать уравнение прямой, проходящей через точку А(—3; 5) и перпендикулярной прямой 4х — Зу—10 = 0.

Решение:

Через точку А проходит пучок прямых, среди которых находится и искомая прямая. Поэтому напишем сначала уравнение этого пучка

Чтобы выделить из него нашу прямую, нужно найти ее угловой коэффициент 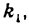связанный с угловым коэффициентом

данной прямой равенством (1). Но 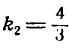следовательно,

Подставив в уравнение (2) вместо 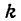найденное его значение

получим:

Это и есть искомое уравнение прямой. Преобразовав его, найдем:

или

Пересечение прямых

Пусть даны две прямые, определяемые уравнениями:

Требуется найти точку их пересечения.

Так как точка пересечения данных прямых есть их общая точка, то ее координаты должны удовлетворять как первому, так и второму уравнению, т. е. эти координаты должны быть общими корнями данных уравнений.

Чтобы найти эти корни, нужно, как известно из алгебры, решить совместно данные уравнения, рассматривая их как систему уравнений.

Пример:

Найти точку пересечения прямых

Решение:

Решим данные уравнения как систему. Умножив второе уравнение на 3 и сложив результат с первым уравнением, получим:

откуда

Зная х, находим у, например, из второго уравнения:

Пример:

Найти точку пересечения прямых

Решение:

Умножив все члены первого уравнения на —2 и сложив полученное уравнение со вторым, найдем:

что невозможно. Значит, данная система уравнений решений не имеет, а потому прямые, определяемые этими уравнениями, не имеют общих точек, т. е. данные прямые параллельны.

К этому же заключению можно прийти, сравнивая угловые коэффициенты данных прямых.

Дополнение к прямой линии

Смотрите также:

Предмет высшая математика

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические функции произвольного угла
84. Тригонометрические формулы
85. Обратные тригонометрические функции
86. Теорема Безу
87. Математическая индукция
88. Показатель степени
89. Показательные функции и логарифмы
90. Множество
91. Множество действительных чисел
92. Числовые множества
93. Преобразование рациональных выражений
94. Преобразование иррациональных выражений
95. Геометрия
96. Действительные числа
97. Степени и корни
98. Степень с рациональным показателем
99. Тригонометрические функции угла
100. Тригонометрические функции числового аргумента
101. Тригонометрические выражения и их преобразования
102. Преобразование тригонометрических выражений
103. Комбинаторика
104. Вычислительная математика
105. Прямая линия на плоскости и ее уравнения
106. Прямая и плоскость
107. Линии и уравнения
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат