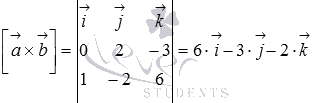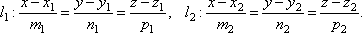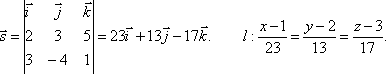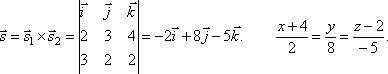Как найти уравнение прямой через вектор - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

Уравнение прямой на плоскости
- Уравнения прямой на плоскости в координатной форме
  - Общее уравнение прямой
  - Параметрическое уравнение прямой
  - Параметрическое уравнение прямой в канонической форме
  - Уравнение прямой, проходящей через две точки
- Уравнения прямой на плоскости в векторной форме
  - Векторное уравнение прямой в параметрической форме
  - Нормальное векторное уравнение прямой
  - Векторное уравнение прямой, проходящей через две точки
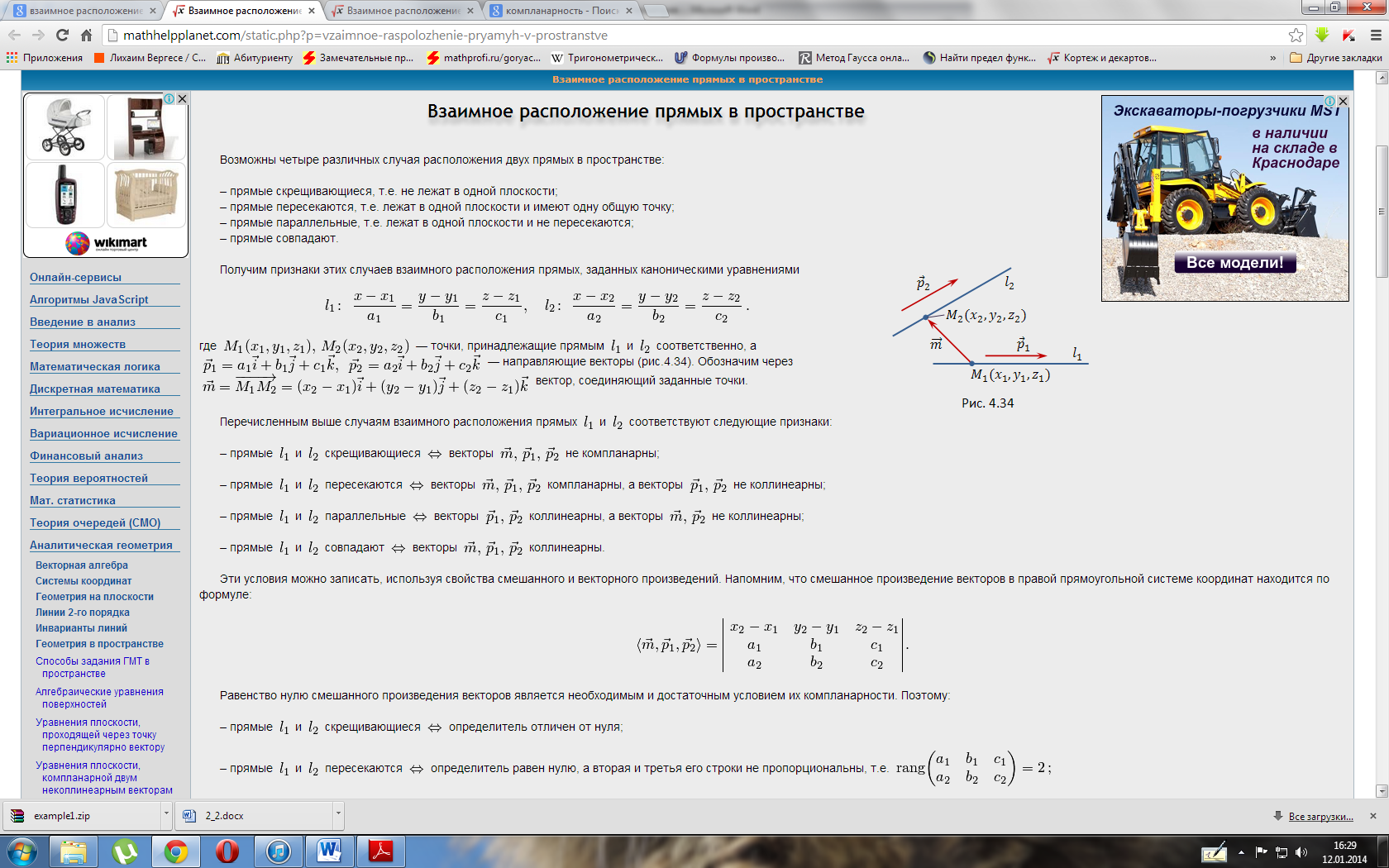
Уравнение прямой в пространстве
- Уравнения прямой в пространстве в координатной форме
  - Параметрические уравнения прямой
  - Параметрические уравнения прямой в канонической форме
  - Уравнение прямой, проходящей через две точки
  - Прямая как пересечение двух плоскостей
- Уравнения прямой в пространстве в векторной форме
  - Векторное уравнение прямой в параметрической форме
  - Векторные уравнения прямой
  - Векторное уравнение прямой, проходящей через две точки

Уравнение прямой на плоскости

Уравнения прямой на плоскости в координатной форме

Любую прямую линию на плоскости можно задать общим уравнением прямой в декартовой системе координат:

то есть числа одновременно не равны нулю.

Прямая линия на плоскости может быть задана параметрическим уравнением прямой:

где числа не равны нулю одновременно. Числа являются компонентами направляющего вектора прямой — ненулевого вектора, лежащего на прямой.

Если то после исключения из уравнений прямой в параметрической форме параметра уравнение прямой приводятся к канонической форме:

$[frac{x - x_0}{alpha} = frac{y - y_0}{beta}.]$

Уравнение прямой, проходящей через две точки и :

$[frac{x - x_1}{x_2 - x_1} = frac{y - y_1}{y_2 - y_1}.]$

При или это уравнение принимает соответственно вид или

Уравнения прямой на плоскости в векторной форме

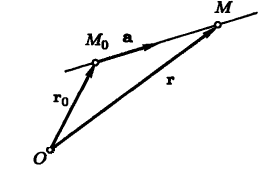
Векторное уравнение прямой в параметрической форме:

$[textbf{r} = textbf{r}_0 + textbf{a}t, qquad textbf{a} ne textbf{0},]$

где — направляющий вектор прямой, $textbf{r}_0$ — радиус-вектор некоторой точки прямой.

Нормальное векторное уравнение прямой:

$[left(textbf{r}-textbf{r}_0, textbf{n}right) = 0, qquad textbf{n} ne textbf{0},]$

где — вектор нормали к прямой.

Это уравнение также можно записать в форме

причём если вектор — единичный, то величина $D = left(textbf{r}_0, textbf{n}right)$ есть расстояние от точки до прямой. Вообще говоря, это уравнение имеет следующий смысл: проекция радиус-вектора любой точки прямой на нормаль к этой прямой постоянна.

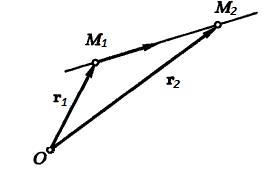
Векторное уравнение прямой, проходящей через две различные точки:

$[textbf{r} = textbf{r}_1 + left(textbf{r}_2 - textbf{r}_1right)t,]$

где $textbf{r}_1$ и $textbf{r}_2$ — радиус-векторы данных точек.

Это уравнение легко получается из векторного уравнения прямой в параметрической форме, если в качестве направляющего вектора прямой взять вектор $textbf{r}_2 - textbf{r}_1.$

Уравнение прямой в пространстве

Уравнение прямой в пространстве в координатной форме

Прямая линия в пространстве может быть задана параметрическими уравнениями:

Числа являются компонентами направляющего вектора прямой.

Исключением параметра параметрические уравнения прямой приводятся к канонической форме:

$[frac{x - x_0}{alpha} = frac{y - y_0}{beta} = frac{z - z_0}{gamma}.]$

Если, например, то канонические уравнения принимают вид

$[frac{x - x_0}{alpha} = frac{y - y_0}{beta},quad z = z_0.]$

Аналогично для любой другой компоненты направляющего вектора.

Если два параметра равны нулю, например, то канонические уравнения имеют вид Аналогично для любых других пар компонент направляющего вектора.

Уравнение прямой в пространстве, проходящей через две точки и :

$[frac{x - x_1}{x_2 - x_1} = frac{y - y_1}{y_2 - y_1} = frac{z - z_1}{z_2 - z_1}.]$

Если, например, то уравнения прямой принимают вид

$[frac{x - x_1}{x_2 - x_1} = frac{y - y_1}{y_2 - y_1}, quad z = z_1.]$

Если к тому же то уравнения прямой записываются в виде Аналогично для любых двух пар совпадающих координат точек.

Прямая в пространстве может быть задана как пересечение двух непараллельных плоскостей:

$begin{equation*} begin{cases} A_1x + B_1y + C_1z + D_1 = 0,\ A_2x + B_2y + C_2z + D_2 = 0. end{cases} end{equation*}$

Уравнение прямой в пространстве в векторной форме

Прямая линия в пространстве может быть задана уравнением в параметрической форме:

$[textbf{r} = textbf{r}_0 + textbf{a}t, qquad textbf{a} ne textbf{0},]$

где — направляющий вектор прямой, $textbf{r}_0$ — радиус-вектор некоторой точки прямой. Это уравнение совпадает с параметрическим векторным уравнением прямой на плоскости.

Прямую в пространстве можно задать векторными уравнениями:

$[left[textbf{r} - textbf{r}_0, textbf{a}right]=textbf{0}, qquad textbf{a} ne textbf{0}]$

или

Векторное уравнение прямой в пространстве, проходящей через две различные точки:

$[textbf{r} = textbf{r}_1 + left(textbf{r}_2 - textbf{r}_1right)t,]$

где $textbf{r}_1$ и $textbf{r}_2$ — радиус-векторы двух точек прямой.

Источник

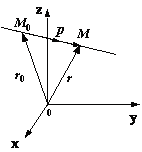
Векторное уравнение прямой в пространстве

Пусть
для прямой известны
ее направляющий вектори
точка,
лежащая на этой прямой. Пусть—
произвольная (текущая) точка прямой.
Обозначим черезиr радиус-векторы
точек исоответственно
(рис. 11.11).

Рис.11.11.Векторное
уравнение прямой

Тогда
вектор коллинеарен
векторуp и,
следовательно, ,
где—
некоторое число. Из рис. 11.11 видно, что

(11.12)

Это
уравнение называется векторным
уравнением прямой
или уравнением
в векторной форме.
При каждом значении параметра мы
будем получать новую точкуна
прямой.

Общие уравнения прямой в пространстве

Линия
в трехмерном пространстве определяется,
вообще говоря, пересечением двух
поверхностей, т.е. описывается системой
двух уравнений.

Прямую
в пространстве можно рассматривать как
линию пересечения двух плоскостей и,
следовательно, описывать системой двух
линейных уравнений

м
н
о

A1x + B1y + C1z + D1 =
0

A2x + B2y + C2z + D2 =
0

при
условии, что эти плоскости непараллельны,
т.е. их нормальные векторы неколлинеарны.

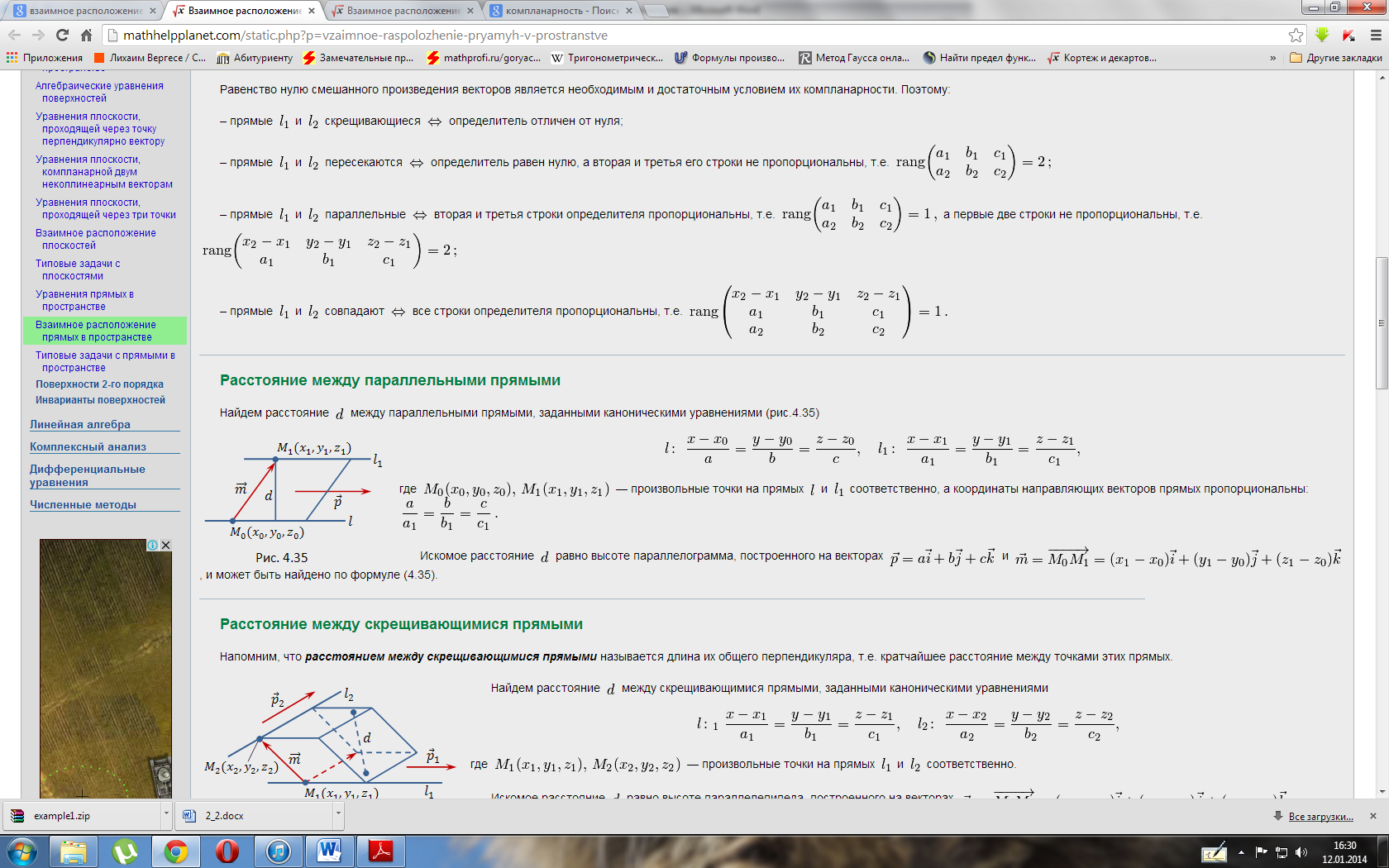
Расстояние
между скрещивающимися прямыми в
пространстве

В
трехмерном пространстве в прямоугольной
системе координат Oxyz заданы две
скрещивающиеся прямые a и b.
Прямую a определяют параметрические
уравнения прямой в пространствевида

X=-2

Y=2t+1

Z=-3t+4

,
а прямую b – канонические
уравнения прямой в пространстве.
Найдите расстояние между заданными
скрещивающимися прямыми.

Очевидно,
прямая a проходит через точку и
имеет направляющий вектор.
Прямая b проходит через точку,
а ее направляющим вектором является
вектор.

Вычислим
векторное произведение векторов и:

Таким
образом, нормальный вектор 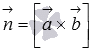плоскости,
проходящей через прямую b параллельно
прямой a, имеет координаты.

Тогда
уравнение плоскости есть
уравнение плоскости, проходящей через
точкуи
имеющей нормальный вектор:

Нормирующий
множитель для общего уравнения
плоскости равен.
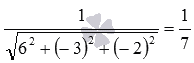
Следовательно, нормальное уравнение
этой плоскости имеет вид.

Осталось
воспользоваться формулой для вычисления
расстояния от точки до
плоскости:

Это
и есть искомое расстояние между заданными
скрещивающимися прямыми.

УГОЛ
МЕЖДУ ПРЯМЫМИ

Углом между
прямыми в пространстве будем называть
любой из смежных углов, образованных
двумя прямыми, проведёнными через
произвольную точку параллельно данным.

Пусть
в пространстве заданы две прямые:

Очевидно,
что за угол φ между прямыми можно принять
угол между их направляющими векторами и.
Так как,
то по формуле для косинуса угла между
векторами получим

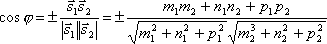
Условия
параллельности и перпендикулярности
двух прямых равносильны условиям
параллельности и перпендикулярности
их направляющих векторов и:

Две
прямые параллельны тогда
и только тогда, когда их соответствующие
коэффициенты пропорциональны,
т.е. l₁ параллельна l₂ тогда
и только тогда, когда параллелен.

Две
прямые перпендикулярны тогда
и только тогда, когда сумма произведений
соответствующих коэффициентов равна
нулю: .

Примеры.

Найти
угол между прямыми и.

Найти
уравнения прямой проходящей через
точку М₁(1;2;3)
параллельно прямой l₁:

Поскольку
искомая прямая l параллельна l₁,
то в качестве направляющего вектора
искомой прямой l можно
взять направляющий вектор прямой l₁.

Составить
уравнения прямой, проходящей через
точку М₁(-4;0;2)
и перпендикулярной прямым: и.

Направляющий
вектор прямой l можно
найти как векторное произведение
векторов и:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.

Здесь будет калькулятор

Уравнение прямой с угловым коэффициентом

y=kx+by=kx+b,

где kk — угловой коэффициент, а bb — свободный коэффициент.

Уравнения данного вида составляются следующим образом по формуле:

y−y0=k(x−x0)y-y_0=k(x-x_0),

где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.

Задача 1

Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.

Решение

Подставляем значения в формулу:

y−y0=k(x−x0)y-y_0=k(x-x_0)

y−2=1⋅(x−1)y-2=1cdot(x-1)

Приводим подобные слагаемые:

y=x+1y=x+1

Ответ

y=x+1y=x+1

Общее уравнение прямой

Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:

y−x−1=0y-x-1=0

Уравнение прямой по двум точкам

Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:

Уравнение прямой по двум точкам

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},

где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.

Задача 2

Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).

Решение

x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}

x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}

x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}

x−4=−y−12x-4=frac{-y-1}{2}

y+1=2⋅(4−x)y+1=2cdot(4-x)

y=8−2x−1y=8-2x-1

y=−2x+7y=-2x+7

Ответ

y=−2x+7y=-2x+7

Уравнение прямой при помощи точки и вектора нормали

Уравнение прямой по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.

Задача 3

Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).

Решение

x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,

x−7+40−5y=0x-7+40-5y=0

x−5y=−40+7x-5y=-40+7

x−5y=−33x-5y=-33

5y=x+335y=x+33

y=x5+335y=frac{x}{5}+frac{33}{5}

Проверка

Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.

8=75+3358=frac{7}{5}+frac{33}{5}

8=88=8 — верно, ответ правильный.

Ответ

y=x5+335y=frac{x}{5}+frac{33}{5}

Прямая в пространстве

Уравнение прямой, заданной в пространстве имеет такой вид:

Уравнение прямой в пространстве

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.

Задача 4

Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).

Решение

x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Проверка

Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:

1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.

Такой вид уравнения прямой называется каноническим.

Ответ

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Тест по теме “Составление уравнения прямой”

Источник

Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x + B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

k = tg φ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки M(x₁, y₁) и N(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂, то уравнение прямой можно найти, используя следующую формулу

x — x₁	=	y — y₁
x₂ — x₁	y₂ — y₁

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x₀y = m t + y₀

где N(x₀, y₀) — координаты точки лежащей на прямой, a = {l, m} — координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки N(x₀, y₀) лежащей на прямой и направляющего вектора a = {l; m} (l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Пример 1. Найти уравнение прямой проходящей через две точки M(1, 7) и N(2, 3).

Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки

x — 12 — 1 = y — 73 — 7

Упростив это уравнение получим каноническое уравнение прямой

x — 11 = y — 7-4

Выразим y через x и получим уравнение прямой с угловым коэффициентом

y — 7 = -4(x — 1)

y = -4x + 11

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 7} = {1; -4}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = -4t + 7

Пример 2. Найти уравнение прямой проходящей через две точки M(1, 3) и N(2, 3).

Решение. Так как M_y — N_y = 0, то невозможно записать уравнение прямой проходящей через две точки.

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 3} = {1; 0}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = 3

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Если прямая проходит через две точки M(x₁, y₁, z₁) и N(x₂, y₂, z₂), такие что x₁ ≠ x₂, y₁ ≠ y₂ и z₁ ≠ z₂, то уравнение прямой можно найти используя следующую формулу

x — x₁	=	y — y₁	=	z — z₁
x₂ — x₁	y₂ — y₁	z₂ — z₁

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x₀
y = m t + y₀
z = n t + z₀

где (x₀, y₀, z₀) — координаты точки лежащей на прямой, {l; m; n} — координаты направляющего вектора прямой.

Каноническое уравнение прямой в пространстве

Если известны координаты точки M(x₀, y₀, z₀) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x — x₀	=	y — y₀	=	z — z₀
l	m	n

Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

	A₁x + B₁y + C₁z + D₁ = 0
A₂x + B₂y + C₂z + D₂ = 0

при условии, что не имеет место равенство

A₁	=	B₁	=	C₁	.
A₂	B₂	C₂

Источник