Уравнение окружности и прямой
Вы будете перенаправлены на Автор24
Уравнение линии на плоскости
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).
Рисунок 1. Произвольная линия в системе координат
Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$
Уравнение окружности
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
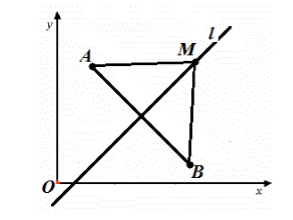
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $left$ и $$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=$, принадлежащую прямой $l$ (рис. 3).
Готовые работы на аналогичную тему
Рисунок 3. Прямая в декартовой системе координат
Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.
Найдем длины данных сторон по формуле расстояния между точками:
Обозначим через $a=2left(x_1-x_2right), b=2left(y_1-y_2right), c=^2+^2-^2-^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:
Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=$, тогда
Если прямая $l$ параллельна оси $Ox$, то она имеет вид
Если прямая $l$ параллельна оси $Oy$, то она имеет вид
Пример задачи на нахождение уравнений линий в декартовой системе координат
Найти уравнение окружности с центром в точке $(2, 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2, 4)$, получим
Найдем радиус окружности как расстояние от точки $(2, 4)$ до точки $(0,0)$
Получаем, уравнение окружности имеет вид:
Найдем теперь уравнение окружности, используя частный случай 1. Получим
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 05 04 2022
Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Уравнение окружности и прямой
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
ТЕМА: «Уравнение окружности и прямой» Цели урока: Повторить уравнение окружности и прямой. Показать применение уравнений окружности и прямой при решении задач. Совершенствование навыков решения задач методом координат.
1. Как называется геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки? Математический диктант Проверить 1. Окружность
2. Как называется хорда, проходящая через центр окружности? Проверить 2. Диаметр
3. Как называется отрезок, соединяющий центр окружности с точкой на окружности? Проверить 3. Радиус
4. Как называется геометрическая фигура, состоящая из множества всех точек плоскости, находящихся от данной точки на расстоянии, не превышающем данного? Проверить 4. Круг
5. Пересекаются ли окружности с центрами А и В, если АВ = 10 см, а радиусы равны 5 см, и 6 см? Проверить 5. Пересекаются
6. Расстояние от центра окружности до точки А равно d, а радиус окружности равен r. Сравните d и r, если точка А лежит вне круга, ограниченного данной окружностью? Проверить 6. d > r
7. Расстояние от центра окружности до точки В равно m, а радиус окружности равен r. Сравните m и r, если точка B лежит внутри круга, ограниченного данной окружностью? Проверить 7. m (0 – 1)2 + (0 + 3)2 = 9 > (0 – 1)2 + (1 + 3)2 = 9 > x
Дана окружность Определите, какие из точек А(-4; 3), В(5; 1), С(-5; 4), D(10; 5) лежат: а) на окружности; б) внутри круга, ограниченного данной окружностью; в) вне круга, ограниченного данной окружностью. (x – 4 )2 + (y + 3)2 = 100 (– 4 – 4)2 + (3 + 3)2 > 100 (5 – 4)2 + (1 + 3)2 100 (10 – 4)2 + (5 + 3)2 = 100
Найдите множество точек, удаленных от окружности на расстояние 3. x 2 + y 2 = 16 x y x 2 + y 2 = 49 x 2 + y 2 = 1
(x + 5)2 + (y – 5)2 = 25 Центр? Радиус? O1(-5;5) r = 5 x y A O O1 450 5 5
Центр? Радиус? x y O1 O E 300 На чертеже расстояние ОО1= , ОЕ – касательная к окружности. EOF = 600. Написать уравнение окружности. ОЕ = ОF, отрезки касательных 6
Домашнее задание п. 93 — 95 № 972(б), 973, 978 (а)
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 937 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 681 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 305 человек из 67 регионов
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 497 938 материалов в базе
Материал подходит для УМК
«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
§ 3. Уравнения окружности и прямой
Дистанционные курсы для педагогов
Другие материалы
- 09.11.2020
- 450
- 30.09.2020
- 347
- 09.01.2020
- 3691
- 21.12.2019
- 1299
- 30.11.2019
- 1196
- 31.10.2019
- 728
- 30.10.2019
- 1992
- 16.08.2019
- 770
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 07.12.2020 969 —> —> —> —>
- PPTX 3 мбайт —> —>
- Оцените материал:
Настоящий материал опубликован пользователем Малышок Елена Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 8 лет и 2 месяца
- Подписчики: 1
- Всего просмотров: 33435
- Всего материалов: 28
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минспорта утвердило программу подготовки киберспортсменов
Время чтения: 1 минута
УрФУ возглавил рейтинг медиаактивности вузов
Время чтения: 1 минута
Каждый второй российский студент недоволен своим вузом
Время чтения: 1 минута
В Сыктывкаре школьников переведут на дистанционное обучение
Время чтения: 1 минута
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
Опубликованы проекты ФГОС по специальностям СПО
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/
http://infourok.ru/uravnenie-okruzhnosti-i-pryamoj-4642598.html
Уравнение окружности и прямой — как между собой связаны
Определение
Окружностью называют замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки, лежащей в аналогичной плоскости, что и кривая. Данная точка является центром окружности.
Записать уравнение окружности можно, используя известные свойства геометрической фигуры:
- Любые точки окружности равноудалены от ее центра. Расстояние является радиусом.
- Зная координаты точек, можно записать формулу для определения расстояния между ними: (|AB|=sqrt{(x_{A}−x_{B})^{2}+(y_{A}−y_{B})^{2}}). Таким образом, квадрат расстояния равен (AB^{2}=(x_{A}−x_{B})^{2}+(y_{A}−y_{B})).
Уравнение для описания окружности, которая имеет радиус R, а ее центр совпадает с точкой (O(x_0;y_0)), имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
((x-x_0)^2+(y-y_0)^2 = R^2)
В том случае, когда центр окружности лежит в точке начала координат, уравнение окружности приобретает упрощенную форму:
(x^2+y^2=R^2)
Предположим, что существует уравнение некой окружности:
((x-1)^2+(y+2)^2=4)
Центром данной геометрической фигуры является точка C(1;-2). Радиус окружности равен R=2.
Определение
Прямая представляет собой линию, которая не имеет начала и не имеет конца, и при этом не искривляется.
Каждую прямую на плоскости можно представить в виде уравнения прямой первой степени. Формула имеет следующий вид:
Ax + By + C = 0
В данном случае А и В не могут одновременно принимать нулевые значения.
С учетом углового коэффициента общее уравнение прямой при значении b, не равном нулю, записывают следующим образом:
y = kx + b
Здесь k является угловым коэффициентом, который можно посчитать, как тангенс угла между рассматриваемой прямой и положительным направлением оси ОХ.
Рассмотрим случай, когда прямая пересекает оси ОХ и ОУ в точках, имеющих следующие координаты:
((a; 0) и (0; b))
Найти рассматриваемую прямую можно с помощью уравнения прямой в отрезках:
(frac{x}{a}+frac{y}{b}=1)
Предположим, что прямая пересекает пару точек (A(x_1;y_1)) и (B(x_2; y_2),) удовлетворяющих данным условиям:
(x_1 ≠ x_2 и y_1 ≠ y_2)
В таком случае уравнение прямой рассчитывают по формуле:
(frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1})
Например, существует некая прямая в прямоугольной системе координат. Данная прямая пересекает пару точек:
(M_1(1;1)) и (M_2(4;2))
Уравнение прямой, проходящей через две обозначенные точки, имеет вид:
(frac{x-1}{4-1}=frac{y-1}{2-1} Leftrightarrow frac{x-1}3=frac{y-1}1)
Преобразуем полученное уравнение:
(frac{x-1}3=frac{y-1}1 Leftrightarrow 1cdot (x-1)=3cdot(y-1) Leftrightarrow x-3y+2=0)
Как составить уравнение прямой, проходящей через центр окружности
Применяя записанные ранее уравнения для прямой и окружности, можно найти уравнение прямой, которая проходит через центр окружности:
(x^2+y^2-6x-8y+16=0)
(x^2+y^2+10x+4y+13=0)
В первую очередь следует рассчитать радиусы и определить координаты центров окружностей:
(x^2 + y^2 — 6x — 8y + 16 = 0)
((x^2 — 6x + 9) + (y^2 — 8y + 16) = 9)
((x — 3)^2 + (y — 4)^2 = 3^2)
(r1 = 3)
(O_1(3;4))
(x^2 + y^2 + 10x + 4y + 13 = 0)
((x^2 + 10x + 25) + (y^2 + 4y + 4) = 16)
((x + 5)^2 + (y + 2)^2 = 4^2)
(r2 = 4)
(O_2(-5;-2))
Уравнение прямой, проходящей через точки (O_1(3;4)) и (O_2(-5;-2)), можно записать следующим образом:
(frac{(x — 3)}{(3 + 5)}=frac{(y — 4)}{(4 + 2)})
(frac{(x — 3)}{8}=frac{(y — 4)}{6})
(3(x — 3) = 4(y — 4))
(3x — 9 = 4y — 16)
(4y = 3x + 7)
(y = frac{3x}{4}+frac{7}{4})
В результате уравнение прямой принимает такой вид:
(y = frac{3x}{4}+frac{7}{4})
Решение задач по теме, примеры
Задача 1
Требуется определить, где находится центр окружности, и чему равен ее радиус. Уравнение окружности:
(x^{2}+(y-3)^{2}=49)
Необходимо представить график окружности в осях абсцисс и ординат.
Решение
Каноническое уравнение окружности имеет вид:
((x-h)^{2}+(y-k)^{2}=r^{2})
В данном случае, центр соответствует О:(h, k), а радиус окружности равен r.
По условиям задачи: (x^{2}+(y-3)^{2}=49)
Таким образом:
(O:(0, 3)qquad r=7)
График:
Ответ: центр совпадает с точкой, имеющей координаты ((0, 3)qquad r=7)
Задача 2
Нужно определить, в какой точке расположен центр окружности, и чему равен ее радиус. Уравнение окружности:
((x+2)^{2}+y^{2}=36)
Решение
В первую очередь следует записать каноническое уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2})
В данном случае, центр окружности совпадает с точкой, имеющей координаты (h, k), а ее радиус равен r.
Согласно условиям задачи:
((x+2)^{2}+y^{2}=36)
Таким образом:
(O:(-2, 0)qquad r=6)
График:
Ответ: центр окружности совпадает с точкой (-2, 0), а ее радиус равен 6.
Задача 3
Требуется преобразовать уравнение в сумму квадратов для расчета радиуса и определения центра окружности:
(2x^{2}+2y^{2}+4x+16y+1=0)
Решение
(2x^{2}+2y^{2}+4x+16y+1=0Longrightarrow x^{2}+y^{2}+2x+8y+frac{1}{2}=0)
В таком случае:
(left(x+1right)^{2}+left( y+4right)^{2}-1-16+frac{1}{2}=0Longrightarrow left(x+1right) ^{2}+left(y+4right) ^{2}=frac{33}{2})
В результате расчетов получим:
центр находится в (-1,-4)
радиус равен (sqrt{frac{33}{2}})
Ответ: (O (-1,-4) и r=sqrt{frac{33}{2}})
Задача 4
Центр окружности совпадает с точкой (4,-5). Необходимо записать уравнение данной окружности, учитывая, что она проходит через точку с координатами (7,-3).
Решение
Каноническое уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2})
Центр находится в точке:
(4,-5)
Радиус соответствует r.
Таким образом:
((x-4)^{2}+(y+5)^{2}=r^{2}Longrightarrow r=sqrt{(x-4)^{2}+(y+5)^{2}})
Учитывая, что окружность проходит через точку (7,-3), запишем:
(r=sqrt{left(3right)^{2}+left(2right)^{2}}=sqrt{13})
Ответ: уравнение окружности имеет вид ((x-4)^{2}+(y+5)^{2}=13)
Задача 5
Необходимо записать уравнение окружности, центр которой соответствует точке O(2,-1), касающейся прямой r:y=x+2. Требуется начертить график.
Решение
Зная, что радиус r является расстоянием, на которое удалены точка O:(h, k) и прямая y-x-2=0, запишем:
(O:(2,-1))
(r=d(O,L)=frac{leftvert -2-1-2rightvert }{sqrt{1^{2}+left( -1right) ^{2}}}=frac{5}{sqrt{2}})
Получим уравнение окружности:
((x-h)^{2}+(y-k)^{2}=r^{2}Longrightarrow (x-2)^{2}+(y+1)^{2}=frac{25}{2})
График:
Ответ: ((x-2)^{2}+(y+1)^{2}=frac{9}{5})
Задача 6
Требуется записать уравнение, описывающее прямую с угловым коэффициентом (k= frac{3}{2}). Искомая прямая пересекает точку А (3;2).
Решение
В первую очередь следует записать стандартную формулу:
(y-y_{0}=k(x-x_{0}))
Применительно к условиям задачи, получим:
(y-(-2)= frac{3}{2} (x-3))
(y+2= frac{3}{2}х-frac{9}{2})
(y= frac{3}{2}х-frac{13}{2})
Ответ: (y= frac{3}{2}х-frac{13}{2})
Пересечение окружности и прямой.Координаты.
| Элементы окружности или координаты |
|
x^2+y^2+ x+ y+ =0 |
| Элементы прямой линии |
| Уравнение окружности |
| Уравнение прямой к угловым коэффициентом |
| Координаты пересечения окружности и прямой |
Рассмотрим более подробно задачу пересечения окружности и прямой. В принципе само решение есть уже в общем виде Пересечение прямой и кривой второго порядка, но мы рассмотрим и выведем формулы точек пересечения этих двух геометрических объектов.
Уравнение прямой, как мы знаем из материала Расчет параметров прямой линии по заданным параметрам могут быть заданы в нескольких видах:
— в общем виде,
— с угловым коэффициентом
— в нормальном виде
Что бы решить нашу первоначальную задачу, использовать будем уравнение прямой с угловым коэффициентом которое имеет вид
Уравнение окружности тоже может быть выражена в различных видах
Например в общем виде оно имеет вид
Подставим в уравнение окружности, уравнение прямой
Раскроем скобки
Или
Мы получили стандартное квадратное уравнение, решив котрое мы получим два значения, которые и будут являтся абсциссами точек пересечения прямой и окружности.
Подставим эти координаты в уравнение прямой, мы получим две ординаты точек пересечения.
Таким образом решение найдено.
Для упрощения, для сверки результатов — калькулятор помогает Вам рассчитать эти точки. Интересная особенность состоит в том, что прямая может быть задана в любом виде, хоть виде двух точек.
А уравнение окружности может быть не только введено с помощью коэффицентов, но и в виде пары трех координат через которые, эта окружность будет проходить.
Рассмотрим вопрос про пересечение прямой с окружностью. Пусть R –
радиус окружности и d – расстояние от центра окружности до прямой. Возьмём
центр окружности за начало координат, а прямую, перпендикулярную к данной, – за
ось х. Тогда уравнением окружности будет
х2 + у2 =
R2,
а уравнение прямой
х = d.
Прямая и окружность пересекаются, если система двух уравнений
х2 + у2 =
R2, х = d
имеет решения. И наоборот, любое решение этой системы даёт координаты х, у точки пересечения прямой с окружностью.
Решив нашу систему, получим:
Из выражения для у видим, что
система имеет два решения, то есть:
– окружность и
прямая пересекаются в двух точках, если R
> d.
Система имеет одно решение,
если:
– прямая и окружность касаются, если R = d.
Система не имеет решений, если:
– прямая и окружность
не пересекаются, если R
< d.
ПРИМЕР:
Найдите точки пересечения окружности
х2 +
у2 =
1
и прямой
у =
2х + 1.
РЕШЕНИЕ:
Так как точки пересечения лежат
на окружности и прямой, то их координаты удовлетворяют систему уравнений:
х2 + у2 =
1, у = 2х + 1.
Решим эту систему. Подставим у из второго уравнения в первое. Получим уравнение
с х:
5х2 + 4х = 0.
Уравнение имеет два корня:
х1 =
0, х2
= –0,8.
Это абсциссы точек пересечения.
Ординаты этих точек получим из уравнения прямой, подставив в него х1 и х2. Получим:
у1 =
1, у2
= –0,6.
Точки пересечения прямой и
окружности будут:
(0; 1), (–0,8; –0,6)
Задания к уроку 30
Используем два уже известных факта и выведем уравнение окружности:
1) все точки окружности находятся на данном расстоянии (радиус) от данной точки (центр);
2) мы имеем формулу для расчёта расстояния между двумя точками, если знаем координаты точек
AB=xA−xB2+yA−yB2
, а если так, то квадрат расстояния
AB2=xA−xB2+yA−yB2
.
Допустим, что центр окружности находится в точке
CxC;yC
, а радиус окружности равен (R).
Любая точка
Px;y
на этой окружности находится на расстоянии (R) от центра (C), значит, справедливо равенство
Это и есть уравнение окружности с центром (C) и радиусом (R). Координаты всех точек, которые находятся на окружности, удовлетворяют уравнению.
Если центр окружности находится в начале координат
0;0
, то уравнение имеет вид
Для выведения уравнения прямой проведём эту прямую как серединный перпендикуляр некоторому отрезку с данными координатами конечных точек отрезка.
Известно, что все точки серединного перпендикуляра находятся на равных расстояниях от концов отрезка.
Координаты концов отрезка
AxA;yA
и
BxB;yB
. Любая точка
Px;y
находится на равных расстояниях от конечных точек
PA=PB
, конечно, равны и квадраты расстояний
PA2=PB2
, значит, справедливо равенство
, которое и есть уравнение прямой.
После возведения выражений в скобках и приведения подобных слагаемых
x2−2⋅x⋅xA+xA2+y2−2⋅y⋅yA+yA2=
=x2−2⋅x⋅xB+xB2+y2−2⋅y⋅yB+yB2;
2⋅x⋅xB−2⋅x⋅xA+2⋅y⋅yB−2⋅y⋅yA+xA2−xB2+yA2−yB2=0;
2xB−2xA⋅x+2yB−2yA⋅y+xA2−xB2+yA2−yB2=0;
уравнение будет в таком виде:
ax+by+c=0;a=2xB−xA;b=2yB−yA;
c=xA2−xB2+yA2−yB2.
Рассмотрим особые прямые.
1. Прямая проходит через некоторую точку на оси (Ox) с координатами
AxA;0
.
Для любой точки на этой прямой
x=xA
, это и есть уравнение прямой.
Так как ось (Oy) проходит через начало координат, то уравнение оси (Oy) есть
x=0
.
2. Прямая проходит через некоторую точку на оси (Oy) с координатами
B0;yB
.
Для любой точки на этой прямой
y=yB
, это и есть уравнение прямой.
Так как ось (Ox) проходит через начало координат, то уравнение оси (Ox) есть
y=0
..

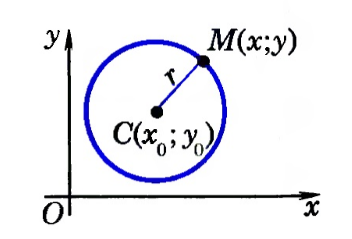






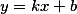
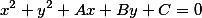
^2+Ax+B(kx+b)+C)
^2+2kbx+b^2+Ax+Bkx+Bb+C=0)
+x(2kb+A+Bk)+b^2+Bb+C=0)






