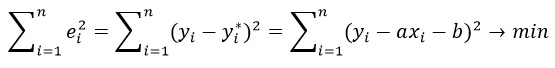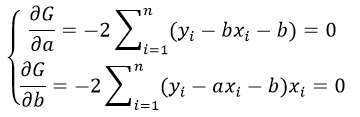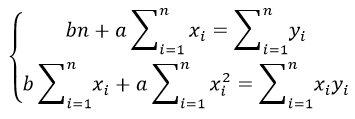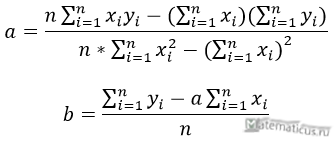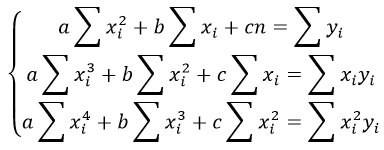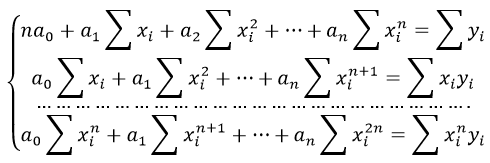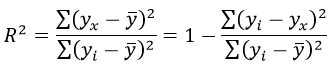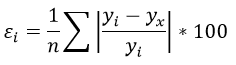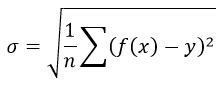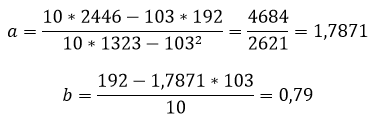Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R2:
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε<10%
Формула среднеквадратической погрешности:
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
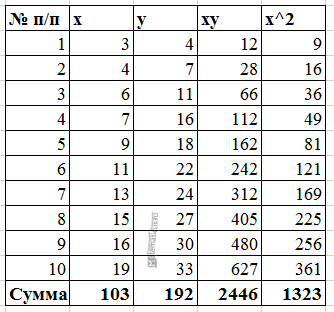
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
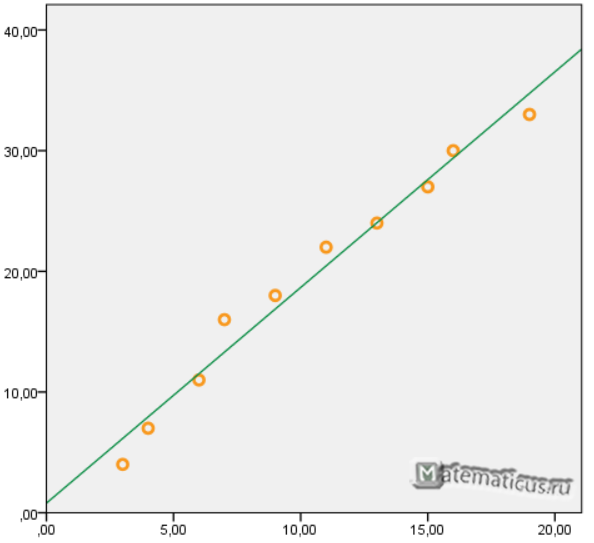
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
16183
Парная линейная регрессия и метод наименьших квадратов (МНК)
Краткая теория
Простейшей системой
корреляционной связи является линейная связь между двумя признаками — парная
линейная корреляция. Практическое значение ее в том, что есть системы, в
которых среди всех факторов, влияющих на результативный признак, выделяется
один важнейший фактор, который в основном определяет вариацию результативного
признака. Измерение парных корреляций составляет необходимый этап в изучении
сложных, многофакторных связей. Есть такие системы связей, при изучении которых
следует предпочесть парную корреляцию. Внимание к линейным связям объясняется
ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные
формы связей для выполнения расчетов преобразуются в линейную форму.
Уравнение парной линейной
корреляционной связи называется уравнением парной регрессии и имеет вид:
где
–
среднее значение результативного признака
при
определенном значении факторного признака
;
– свободный
член уравнения;
– коэффициент
регрессии, измеряющий среднее отношение отклонения результативного признака от
его средней величины к отклонению факторного признака от его средней величины
на одну единицу его измерения – вариация
, приходящаяся на единицу вариации
.
Параметры уравнения
находят
методом наименьших квадратов (метод решения систем уравнений, при котором в
качестве решения принимается точка минимума суммы квадратов отклонений), то
есть в основу этого метода положено требование минимальности сумм квадратов
отклонений эмпирических данных
от
выровненных
:
Для нахождения минимума
данной функции приравняем к нулю ее частные производные.
В результате получим
систему двух линейных уравнений, которая называется системой нормальных
уравнений:
Решая эту систему в общем
виде, получим:
Параметры уравнения парной
линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же
результат:
или
Если
коэффициент линейной корреляции
уже
рассчитан, то легко может быть найден коэффициент
парной
регрессии:
где
,
– стандартные
отклонения.
Примеры решения задач
Задача 1
Имеются следующие данные о
цене на нефть
(ден.
ед.) и индексе акций нефтяных компаний
(усл.
ед.).
| Цена на нефть (ден. ед.) | 17,28 | 17,05 | 18,30 | 18,80 | 19,20 | 18,50 |
| Индекс акций (усл. ед.) | 537 | 534 | 550 | 555 | 560 | 552 |
- Построить
корреляционное поле. - Предполагая, что между
переменными x и y существует линейная зависимость, найти уравнение линейной
регрессии - Оценить тесноту связи.
Решение
Построим корреляционное
поле, для этого отметим в системе координат
6 точек, соответствующих данным парам значений этих признаков.
Корреляционное поле и линия регрессии
Расположение точек на
рисунке показывает, что зависимость между компонентами
и
двумерной дискретной случайной величины может
выражаться линейным уравнением регрессии
.
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
|
|
|
|
|
|
|
| 1 | 17,28 | 537 | 298,5984 | 288369 | 9279,36 |
| 2 | 17,05 | 534 | 290,7025 | 285156 | 9104,7 |
| 3 | 18,3 | 550 | 334,89 | 302500 | 10065 |
| 4 | 18,8 | 555 | 353,44 | 308025 | 10434 |
| 5 | 19,2 | 560 | 368,64 | 313600 | 10752 |
| 6 | 18,5 | 552 | 342,25 | 304704 | 10212 |
| Сумма | 109,13 | 3288 | 1988,521 | 1802354 | 59847,06 |
Коэффициенты
уравнения регрессии
можно найти методом наименьших квадратов,
решив систему нормальных уравнений:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Подставляя
в систему уравнений числовые значения, получаем:
Решая
систему уравнений, получаем:
Уравнение
парной линейной регрессии:
Коэффициент линейной корреляции
вычислим по формуле:
Вывод
Таким
образом уравнение линейной регрессии, устанавливающее зависимость между ценой
на нефть и индексом акций имеет вид
— с увеличением цены на нефть на 1 ден.ед.
цена акций увеличивается на 12,078 ед. Коэффициент корреляции очень близок к
единице — между исследуемыми величинами существует очень тесная связь.
Задача 2
По
территории региона приводятся данные за 2011 г.
Требуется:
-
Построить линейное уравнение парной регрессии
от
.
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку
аппроксимации.
Оценить статистическую значимость параметров регрессии и корреляции с помощью
–критерия Фишера и
–критерия Стьюдента.
Выполнить прогноз заработной платы
при прогнозном значении среднедушевого
прожиточного минимума
, составляющем
107% от среднего уровня.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный
интервал.
На одном графике построить исходные данные и теоретическую прямую.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение линейной парной регрессии
1)
Для расчета параметров уравнения линейной регрессии строим расчетную таблицу:
Получено
уравнение линейной регрессии
Вывод
С
увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная
заработная плата возрастает в среднем на 1.012 руб.
Коэффициент линейной корреляции
2)
Теснота линейной связи оценивается с помощью
коэффициента корреляции
:
Коэффициент
детерминации:
Вывод
Это
означает, что 69.2% вариации заработной платы
объясняется вариацией фактора
–среднедушевого прожиточного минимума.
Средняя ошибка аппроксимации
Качество
модели можно оценить с помощью средней ошибки аппроксимации:
Вывод
Качество
построенной модели оценивается как хорошее, так как средняя ошибка
аппроксимации не превышает 8-10%.
F-критерий
3)
Рассчитаем
– критерий.
По таблице F-распределения Фишера-Снедекора, при уровне значимости α=0,05 и числе степеней свободы k1=1 и k2=12-2=10, критическое значение:
Вывод
– гипотеза о статистической незначимости
уравнения регрессии отклоняется.
Статистическая значимость параметров регрессии
Оценку
статистической значимости параметров регрессии проведем с помощью
t–статистики Стьюдента
и путем расчета
доверительного интервала каждого из показателей.
Выдвигаем
гипотезу
о статистически незначимом отличии показателей
от нуля:
для числа степеней свободы
и
составит 2,23
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Определим
случайные ошибки
Тогда:
Фактическое значение превосходит
табличное значение t–статистики.
Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Рассчитаем
доверительные интервалы для параметров регрессии
и
. Для этого
определим предельную ошибку для каждого показателя:
Доверительные
интервалы:
или
или
Точечный прогноз
4)
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение прожиточного минимума составит
руб., тогда прогнозное значение среднедневной
заработной платы составит:
Интервальный прогноз
5)
Ошибка прогноза составит:
Предельная
ошибка прогноза, которая в 95% случаев не будет превышена, составит:
Доверительный
интервал прогноза:
6) Построим исходные данные
и теоретическую прямую:
Корреляционное поле и прямая уравнения регрессии
При проведении
современных клинических исследований
обычно нет недостатка в информации:
каждому пациенту соответствует целое
множество различных клинических
показателей и данных.
В них могут быть
завуалированы некоторые соотношения,
основные черты которых и позволяют
выявлять методы регрессионного анализа.
При этом задача
регрессионного анализа состоит в
подборе упрощенной аппроксимации этой
связи с помощью математической модели.
Регрессионный
анализ имеет в своем распоряжении
специальные процедуры проверки, является
ли выбранная математическая модель
адекватной
для описания
имеющихся данных.
Чаще
всего регрессионный анализ используется
для прогноза,
то есть
предсказания значений ряда зависимых
переменных по известным значениям
других переменных.
Выше указывалось,
что результаты наблюдений, приведенные
в двумерной выборке:
|
xi |
x1 |
x2 |
x3 |
x4 |
x5 |
|
yi |
y1 |
y2 |
y3 |
y4 |
y5 |
можно
представить в виде корреляционного
поля точек (рис. 14.3), где каждая точка
соответствует отдельным значениям х
и у.
Рис.
14.3. Метод
наименьших квадратов
В
результате получается диаграмма
рассеяния, позволяющая судить о форме
и тесноте связи между варьирующими
признаками. Довольно часто эта связь
может быть аппроксимирована прямой
линией (рис. 14.3).
Регрессия
— это функция,
позволяющая по величине одного признака
X
находить среднее ожидаемое (должное)
значение другого признака Y,
корреляционно
связанного с X.
В линейной
математической модели уравнение
линейной регрессии имеет вид:
,
где
а и
b
— параметры
линейной регрессии;
а
— это
коэффициент регрессии, показывающий,
насколько в среднем величина одного
признака Y
изменяется при изменении на единицу
меры другого признака X,
корреляционно
связанного с Y.
Чем больше
a
— угловой коэффициент прямой а=
tg
α, тем круче прямая, то есть быстрее
изменяется Y.
b
— свободный
член в уравнении, определяет
;
при x
= 0.
—
это предсказанное (должное) значение
Y
для данного
х при
определенных значениях регрессионных
параметров.
Параметры линейной
регрессии определяют методом наименьших
квадратов — это способ подбора параметров
регрессионной модели, согласно которому
сумма квадратов отклонений вариант от
линии регрессии должна быть минимальна:
Это эффективный
метод, позволяющий уменьшить влияние
ошибок измерений.
Теперь
определяют должные величины
,наносят эти
точки и соединяют их прямой линией.
Достоинство
корреляционно-регрессионного анализа
— наглядное представление о форме и
тесноте связи. Регрессия выражает
корреляционную зависимость в виде
функционального
отношения и
дает более полную информацию.
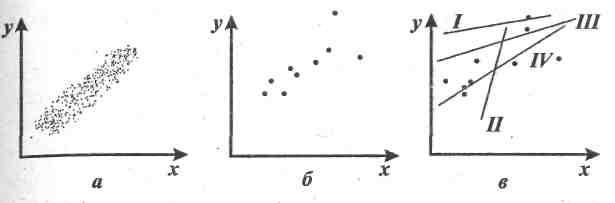
Была
исследована зависимость между ростом
(X)
и массой
(Y),
у 200 животных и рост, и масса подчиняются
нормальному закону распределения. На
рис. 3а видно, что эта зависимость
линейная: чем больше рост, тем больше
масса.
Из
этой совокупности выберем выборку
объема п =
10 (рис. 13.4б). Сохранилась ли эта зависимость
массы от роста? На рис. 13.4б изображены
4 прямые, аппроксимирующие эту зависимость.
Какую прямую можно считать наилучшей?
Рис
14.4. Зависимость
между ростом (X)
и массой (Y)
у животных
Ответ:
Да, сохранилась.
Прямая I
— не годится — все точки оказались по
одну сторону от нее. Прямая II
– слишком круто устремляется вверх.
Лучше
прямые III
и IV,
а из них лучше та, которая ближе ко всем
точкам выборки, то есть относительно
которой разброс точек минимален.
Согласно
методу наименьших квадратов лучше
представляет зависимость
от х
прямая IV.
По данным примера
№ 2:
|
Xi |
31 |
32 |
33 |
34 |
35 |
35 |
40 |
41 |
42 |
46 |
|
Yi |
7,8 |
8,3 |
7,6 |
9,1 |
9,6 |
9,8 |
11,8 |
12,1 |
14,7 |
13,0 |
Рассчитать
параметры уравнения регрессии
по формулам:
Решение:
Именно
это уравнение задает прямую IV
в задаче № 6.
В
примере № 2 был рассчитан коэффициент
корреляции между ростом (X)
и массой
(Y)
некоторых животных, а
в примере
№ 7 было составлено уравнение линейной
регрессии.
Как
вы думаете, если поменять х
и
у, то изменится
ли уравнение регрессии и коэффициент
корреляции?
Ответ:
r
— останется
прежним, r
= 0,925 — он
симметричен, а уравнение регрессии
получится другим. Получается, что связь
роста с массой одна, а роста с массой —
другая. Регрессионный анализ асимметричен
— это мешает его использовать для
характеристики силы связи.
Провести
корреляционно-регрессионный анализ.
Построить корреляционное поле точек,
проверить значимость (α ≤ 0,05) коэффициента
корреляции между переменными X
и Y
и построить
линию регрессии.
Изучали
зависимость между содержанием вещества
X
в ткани С и
приростом концентрации вещества Y
в
крови у
пациентов, получавших препарат А.
Результаты
наблюдений приведены в виде двумерной
выборки объема 10:
|
xi |
1,15 |
1,9 |
3 |
5,34 |
5,4 |
7,7 |
7,9 |
9,03 |
9,37 |
10,18 |
|
yi |
0,99 |
0,98 |
2,6 |
5,92 |
4,33 |
7,68 |
9,8 |
9,47 |
10,64 |
12,9 |
Результаты
расчета на компьютере:
r
= 0,94;
tнабл
= 6,17;
= 0,579 + 1,1354 ∙
х
Решение:
Н0:
rген
= 0; Н1:
rген
≠ 0.
Найдем
из таблицы tкрит
= 2,31; α ≤
0,05;
f
= 10 — 2 = 8.
Сравним:
tнабл
> tкрит(α,
f);
6,17 > 2,31.
Отвергается
H0
принимается
H1.
Имеется
очень сильная линейная корреляционная
связь между признаками r
= 0,94 (α ≥
0,05).
Построим
корреляционное поле точек (рис. 13.5).
Рис.
13.5.
График
решения задачи 9
Рассчитаем должные
величины:
при
x
= 0,
= -0,576;
при
х = 1,
=0,556.
Нанесем линию
регрессии на график.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
12.03.201615.15 Mб32Малышев В.Д — Интенсивная терапия. 2002.djvu
- #
- #
- #
- #
- #
13.02.201545.54 Mб45Математический анализ.pdf
- #
- #
- #
- #
Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Решения задач: метод наименьших квадратов
Метод наименьших квадратов применяется для решения различных математических задач и основан на минимизации суммы квадратов отклонений функций от исходных переменных. Мы рассмотриваем его приложение к математической статистике в простейшем случае, когда нужно найти зависимость (парную линейную регрессию) между двумя переменными, заданными выборочными данным. В этом случае речь идет об отклонениях теоретических значений от экспериментальных.
Краткая инструкция по методу наименьших квадратов для чайников: определяем вид предполагаемой зависимости (чаще всего берется линейная регрессия вида $y(x)=ax+b$), выписываем систему уравнений для нахождения параметров $a, b$. По экспериментальным данным проводим вычисления и подставляем значения в систему, решаем систему любым удобным методом (для размерности 2-3 можно и вручную). Получается искомое уравнение.
Иногда дополнительно к нахождению уравнения регрессии требуется: найти остаточную дисперсию, сделать прогноз значений, найти значение коэффициента корреляции, проверить качество аппроксимации и значимость модели. Примеры решений вы найдете ниже. Удачи в изучении!
Примеры решений МНК
Пример 1. Методом наименьших квадратов для данных, представленных в таблице, найти линейную зависимость
Пример 2. Прибыль фирмы за некоторый период деятельности по годам приведена ниже:
Год 1 2 3 4 5
Прибыль 3,9 4,9 3,4 1,4 1,9
1) Составьте линейную зависимость прибыли по годам деятельности фирмы.
2) Определите ожидаемую прибыль для 6-го года деятельности. Сделайте чертеж.
Пример 3. Экспериментальные данные о значениях переменных х и y приведены в таблице:
1 2 4 6 8
3 2 1 0,5 0
В результате их выравнивания получена функция Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Пример 4. Данные наблюдений над случайной двумерной величиной (Х, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X.
Пример 5. Считая, что зависимость между переменными x и y имеет вид $y=ax^2+bx+c$, найти оценки параметров a, b и c методом наименьших квадратов по выборке:
x 7 31 61 99 129 178 209
y 13 10 9 10 12 20 26
Пример 6. Проводится анализ взаимосвязи количества населения (X) и количества практикующих врачей (Y) в регионе.
Годы 81 82 83 84 85 86 87 88 89 90
X, млн. чел. 10 10,3 10,4 10,55 10,6 10,7 10,75 10,9 10,9 11
Y, тыс. чел. 12,1 12,6 13 13,8 14,9 16 18 20 21 22
Оцените по МНК коэффициенты линейного уравнения регрессии $y=b_0+b_1x$.
Существенно ли отличаются от нуля найденные коэффициенты?
Проверьте значимость полученного уравнения при $alpha = 0,01$.
Если количество населения в 1995 году составит 11,5 млн. чел., каково ожидаемое количество врачей? Рассчитайте 99%-й доверительный интервал для данного прогноза.
Рассчитайте коэффициент детерминации
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.
- Остатки нормально распределены с нулевым средним значением;
- Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.
Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
http://www.matburo.ru/ex_ms.php?p1=msmnk
http://statistica.ru/theory/osnovy-lineynoy-regressii/
Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.
Одна переменная x известна как предикторная переменная .
Другая переменная, y , известна как переменная ответа .
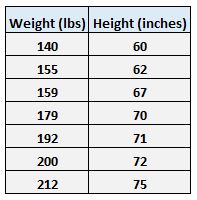
Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:
Пусть вес будет предикторной переменной, а рост — переменной отклика.
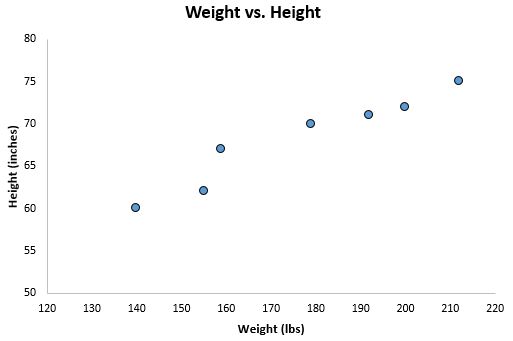
Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:
Предположим, нам интересно понять взаимосвязь между весом и ростом. На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.
Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным. Эта линия известна как линия регрессии наименьших квадратов, и ее можно использовать, чтобы помочь нам понять взаимосвязь между весом и ростом. Обычно вы должны использовать программное обеспечение, такое как Microsoft Excel, SPSS или графический калькулятор, чтобы найти уравнение для этой линии.
Формула линии наилучшего соответствия записывается так:
ŷ = б 0 + б 1 х
где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.
Связанный: 4 примера использования линейной регрессии в реальной жизни
Поиск «Линии наилучшего соответствия»
Для этого примера мы можем просто подключить наши данные к калькулятору линейной регрессии Statology и нажать « Рассчитать »:
Калькулятор автоматически находит линию регрессии методом наименьших квадратов :
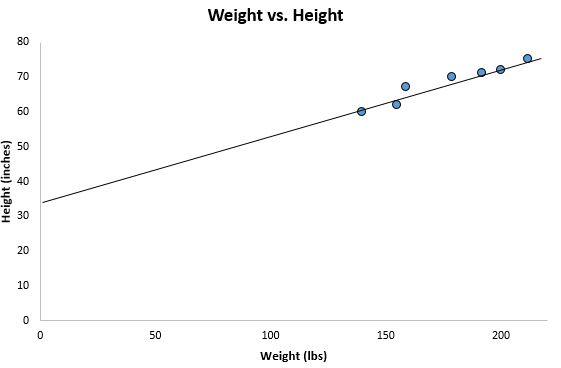
ŷ = 32,7830 + 0,2001x
Если мы уменьшим масштаб нашей диаграммы рассеяния и добавим эту линию на диаграмму, вот как это будет выглядеть:
Обратите внимание, как наши точки данных близко разбросаны вокруг этой линии. Это потому, что эта линия регрессии методом наименьших квадратов лучше всего подходит для наших данных из всех возможных линий, которые мы могли бы нарисовать.
Как интерпретировать линию регрессии методом наименьших квадратов
Вот как интерпретировать эту линию регрессии наименьших квадратов: ŷ = 32,7830 + 0,2001x
б0 = 32,7830.Это означает, что когда предикторная переменная веса равна нулю фунтов, прогнозируемый рост составляет 32,7830 дюйма. Иногда может быть полезно знать значение b 0 , но в этом конкретном примере на самом деле нет смысла интерпретировать b 0 , поскольку человек не может весить ноль фунтов.
б 1 = 0,2001.Это означает, что увеличение x на одну единицу связано с увеличением y на 0,2001 единицы. В этом случае увеличение веса на один фунт связано с увеличением роста на 0,2001 дюйма.
Как использовать линию регрессии наименьших квадратов
Используя эту линию регрессии наименьших квадратов, мы можем ответить на такие вопросы, как:
Какого роста мы ожидаем от человека, который весит 170 фунтов?
Чтобы ответить на этот вопрос, мы можем просто подставить 170 в нашу линию регрессии для x и найти y:
ŷ = 32,7830 + 0,2001 (170) = 66,8 дюйма
Какого роста мы ожидаем от человека, который весит 150 фунтов?
Чтобы ответить на этот вопрос, мы можем подставить 150 в нашу линию регрессии для x и найти y:
ŷ = 32,7830 + 0,2001 (150) = 62,798 дюйма
Предупреждение. При использовании уравнения регрессии для ответа на подобные вопросы убедитесь, что вы используете только те значения переменной-предиктора, которые находятся в пределах диапазона переменной-предиктора в исходном наборе данных, который мы использовали для создания линии регрессии методом наименьших квадратов. Например, вес в нашем наборе данных варьировался от 140 до 212 фунтов, поэтому имеет смысл отвечать на вопросы о прогнозируемом росте только тогда, когда вес составляет от 140 до 212 фунтов.
Коэффициент детерминации
Одним из способов измерения того, насколько хорошо линия регрессии наименьших квадратов «соответствует» данным, является использование коэффициента детерминации , обозначаемого как R 2 .
Коэффициент детерминации — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.
Коэффициент детерминации может варьироваться от 0 до 1. Значение 0 указывает на то, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
R 2 между 0 и 1 указывает, насколько хорошо переменная отклика может быть объяснена переменной-предиктором. Например, R 2 , равный 0,2, указывает, что 20% дисперсии переменной отклика можно объяснить переменной-предиктором; R 2 , равное 0,77, указывает, что 77% дисперсии переменной отклика можно объяснить переменной-предиктором.
Обратите внимание, что в нашем предыдущем выводе мы получили значение R2, равное 0,9311 , что указывает на то, что 93,11% изменчивости роста можно объяснить предикторной переменной веса:
Это говорит нам о том, что вес является очень хорошим предиктором роста.
Предположения линейной регрессии
Чтобы результаты модели линейной регрессии были достоверными и надежными, нам необходимо проверить выполнение следующих четырех допущений:
1. Линейная зависимость. Существует линейная зависимость между независимой переменной x и зависимой переменной y.
2. Независимость: Остатки независимы. В частности, нет корреляции между последовательными остатками в данных временных рядов.
3. Гомоскедастичность: остатки имеют постоянную дисперсию на каждом уровне x.
4. Нормальность: остатки модели нормально распределены.
Если одно или несколько из этих предположений нарушаются, то результаты нашей линейной регрессии могут быть ненадежными или даже вводящими в заблуждение.
Обратитесь к этому сообщению для объяснения каждого предположения, как определить, выполняется ли предположение, и что делать, если предположение нарушается.