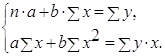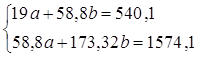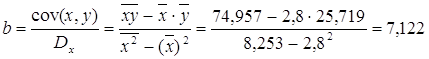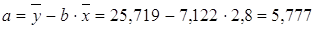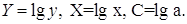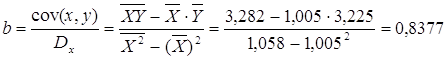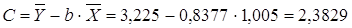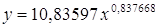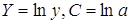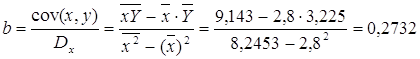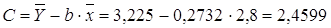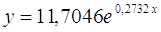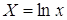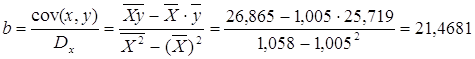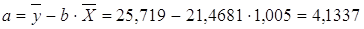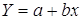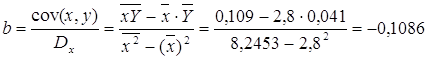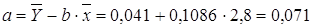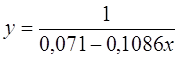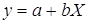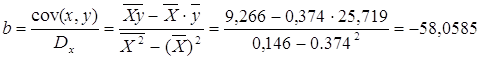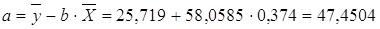Нелинейные модели парной регрессии
- Параболическая регрессия
- Гиперболическая регрессия
- Показательная (экспоненциальная) регрессия)
- Степенная регрессия
Параболическая регрессия
Уравнение регрессии в
форме параболы второго порядка имеет следующий вид:
Если при линейной связи
среднее изменение результативного признака на единицу фактора постоянно по всей
области вариации фактора, то при параболической корреляции изменение признака
меняется
равномерно с изменением величины фактора. В результате связь может даже
поменять знак на противоположный, из прямой превратится в обратную, из обратной в прямую. Такой характер связи присущ многим системам. Например, с увеличением дозы
удобрений урожайность сельхозкультур сначала
повышается, но если превысить оптимальную величину дозы, то при дальнейшем
росте дозы удобрения растения угнетаются и урожайность снижается.
Нормальные уравнения
метода наименьших квадратов (МНК) для параболы 2-го порядка таковы:
Ввиду симметричности
кривой парабола второй степени далеко не всегда пригодна в конкретных
исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами
параболы, а не с полной параболической формой.
Кроме того, параметры
параболической связи не всегда могут быть логически истолкованы. Поэтому если
график зависимости не демонстрирует четко выраженной параболы второго порядка
(нет смены направленности связи признаков), то она может быть заменена другой
нелинейной функцией, например степенной. В частности, в литературе часто
рассматривается парабола второй степени для характеристики зависимости
урожайности от количества внесенных удобрений. Данная форма связи мотивируется
тем, что с увеличением количества внесенных удобрений урожайность растет лишь
до достижения оптимальной дозы вносимых удобрений. Дальнейший же рост их дозы
оказывается вредным для растения, и урожайность снижается. Несмотря на несомненную
справедливость данного утверждения, следует отметить, что внесение в почву
минеральных удобрений производится на основе учета достижений агробиологической
науки. Поэтому на практике часто данная зависимость представлена лишь сегментом
параболы, что и позволяет использовать другие нелинейные функции.
Задача 1
Постройте
криволинейную регрессионную модель (параболу) для следующих исходных данных.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение параболической
регрессии имеет вид:
Составим
расчетную таблицу:
Для
нахождения коэффициентов параболы необходимо решить систему уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Уравнение
параболической регрессии имеет вид:
Коэффициент
детерминации:
Коэффициент эластичности:
Гиперболическая регрессия
Уравнение регрессии в
форме гиперболы имеет следующий вид:
Гиперболические
зависимости характерны для связей, в которых результативный признак не может
варьировать неограниченно, его вариация имеет односторонний предел. Например,
совершенствуя двигатель, можно увеличивать его КПД, но не выше предела, допускаемого
данным видом преобразования энергии. Или таков характер связи между уровнем
душевого дохода в семье и долей семей, имеющих телевизоры – он приближен к
пределу (100%) в наиболее обеспеченной группе семей.
Если величина
положительна, то при увеличении значений
факторного признака
значения
результативного признака уменьшаются, причем это уменьшение все время
замедляется, и при
средняя
величина признака
будет
равна
. Классическим примером является кривая Филлипса, характеризующая нелинейное соотношение между
нормой безработицы
и
процентом прироста заработной платы.
Если же параметр
отрицателен,
то значения результативного признака с ростом фактора возрастают, причем их
рост замедляется, и в пределе при
. Примером может служить взаимосвязь доли
расходов на товары длительного пользования и общих сумм расходов.
Математическое описание подобного рода взаимосвязей получило название кривых Энегеля.
Нормальные уравнения
метода наименьших квадратов (МНК) для гиперболы таковы:
Легко увидеть, что эти
уравнения, по существу, те же, что для линейной связи. Линеаризация гиперболического
уравнения достигается заменой
на
новую переменную, которую можно обозначить
. Тогда уравнение гиперболической регрессии
примет вид
.
Задача 2
Постройте
криволинейную регрессионную модель (гиперболу) для следующих исходных данных.
|
|
0,96 | 0,75 | 0,64 | 0,55 | 0,68 | 0,71 | 0,95 | 0,45 | 0,71 | 0,63 |
|
|
1,95 | 2,6 | 4,28 | 6,52 | 4,55 | 2,91 | 1,81 | 8,21 | 2,84 | 4,38 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение гиперблической регрессии имеет вид:
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
| № |
|
|
|
|
|
|
|
|
| 1 | 0,96 | 1,95 | 1,042 | 1,085 | 2,031 | 1,436 | 6,598 | 4,223 |
| 2 | 0,75 | 2,6 | 1,333 | 1,778 | 3,467 | 3,105 | 0,809 | 1,974 |
| 3 | 0,64 | 4,28 | 1,563 | 2,441 | 6,688 | 4,417 | 0,169 | 0,076 |
| 4 | 0,55 | 6,52 | 1,818 | 3,306 | 11,855 | 5,880 | 3,514 | 6,325 |
| 5 | 0,68 | 4,55 | 1,471 | 2,163 | 6,691 | 3,891 | 0,013 | 0,297 |
| 6 | 0,71 | 2,91 | 1,408 | 1,984 | 4,099 | 3,535 | 0,221 | 1,199 |
| 7 | 0,95 | 1,81 | 1,053 | 1,108 | 1,905 | 1,499 | 6,279 | 4,818 |
| 8 | 0,45 | 8,21 | 2,222 | 4,938 | 18,244 | 8,192 | 17,527 | 17,682 |
| 9 | 0,71 | 2,84 | 1,408 | 1,984 | 4,000 | 3,535 | 0,221 | 1,357 |
| 10 | 0,63 | 4,38 | 1,587 | 2,520 | 6,952 | 4,559 | 0,306 | 0,141 |
| Итого | 7,03 | 40,05 | 14,905 | 23,306 | 65,932 | 40,048 | 35,658 | 38,092 |
Для
нахождения коэффициентов гиперболической регрессии необходимо решить систему
уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Искомое уравнение гиперболической
регрессии:
Коэффициент
детерминации:
Коэффициент эластичности:
Показательная (экспоненциальная) регрессия
Уравнение регрессии в
показательной форме имеет следующий вид:
Данное
уравнение является нелинейным по коэффициенту
и относится к классу моделей регрессии,
которые можно с помощью преобразований привести к линейному виду.
Показательная функция
является внутренне линейной, поэтому оценки неизвестных параметров её
линеаризованной формы можно рассчитать с помощью классического метода
наименьших квадратов
Нормальные уравнения
метода наименьших квадратов (МНК) для показательной регрессии:
Отсюда:
Задача 3
Постройте
криволинейную регрессионную модель (показательная функция) для следующих
исходных данных.
|
|
1,95 | 2,58 | 3,26 | 4,51 | 5,14 | 5,92 | 6,81 | 7,45 | 8,02 | 8,75 |
|
|
6,1 | 8,51 | 10,82 | 17,92 | 24,21 | 33,1 | 45,51 | 61,21 | 72,38 | 95,24 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение показательной
регрессии имеет вид:
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
| № |
|
|
|
|
|
|
|
|
| 1 | 1,95 | 6,1 | 3,803 | 1,808 | 3,526 | 6,433 | 0,104 | 985,960 |
| 2 | 2,58 | 8,51 | 6,656 | 2,141 | 5,524 | 8,292 | 0,048 | 840,420 |
| 3 | 3,26 | 10,82 | 10,628 | 2,381 | 7,763 | 10,904 | 0,007 | 711,822 |
| 4 | 4,51 | 17,92 | 20,340 | 2,886 | 13,015 | 18,041 | 0,015 | 383,376 |
| 5 | 5,14 | 24,21 | 26,420 | 3,187 | 16,380 | 23,252 | 0,918 | 176,624 |
| 6 | 5,92 | 33,1 | 35,046 | 3,500 | 20,717 | 31,835 | 1,600 | 19,360 |
| 7 | 6,81 | 45,51 | 46,376 | 3,818 | 26,000 | 45,561 | 0,003 | 64,160 |
| 8 | 7,45 | 61,21 | 55,503 | 4,114 | 30,652 | 58,959 | 5,066 | 562,164 |
| 9 | 8,02 | 72,38 | 64,320 | 4,282 | 34,341 | 74,176 | 3,226 | 1216,614 |
| 10 | 8,75 | 95,24 | 76,563 | 4,556 | 39,869 | 99,532 | 18,423 | 3333,908 |
| Итого | 54,39 | 375 | 345,654 | 32,674 | 197,788 | 29,408 | 8294,409 |
Для
нахождения коэффициентов показательной регрессии необходимо решить систему
уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Искомое уравнение показательной
регрессии:
Коэффициент
детерминации:
Коэффициент эластичности:
Степенная регрессия
В моделях, нелинейных по
оцениваемым параметрам, но приводимых к линейному виду, метод наименьших
квадратов и его требования применяются не к исходным данным результативного
признака, а к их преобразованным величинам.
Так, в степенной функции:
метод наименьших квадратов
применяется к преобразованному уравнению:
Система линейных уравнений
будет иметь вид:
Отсюда:
Степенная регрессия широко
используется в исследованиях при изучении эластичности спроса от цен.
Задача 4
По данным постройте
степенную регрессию:
|
|
2,21 | 17,45 | 8,6 | 61,05 | 5,76 | 33,38 | 16,22 | 3,88 | 0,75 | 149,3 |
|
|
9,63 | 25,92 | 31,6 | 17,71 | 14,87 | 44,03 | 13,7 | 9,13 | 3,86 | 170,45 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение степенной
регрессии имеет вид:
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
| № |
|
|
|
|
|
|
|
|
|
| 1 | 2,21 | 9,63 | 0,793 | 0,629 | 2,265 | 1,796 | 8,690 | 105,030 | 86,655 |
| 2 | 17,45 | 25,92 | 2,859 | 8,176 | 3,255 | 9,307 | 20,871 | 3,733 | 48,736 |
| 3 | 8,6 | 31,6 | 2,152 | 4,630 | 3,453 | 7,430 | 15,461 | 12,093 | 160,304 |
| 4 | 61,05 | 17,71 | 4,112 | 16,906 | 2,874 | 11,818 | 35,494 | 274,065 | 1,510 |
| 5 | 5,76 | 14,87 | 1,751 | 3,066 | 2,699 | 4,726 | 13,045 | 34,739 | 16,556 |
| 6 | 33,38 | 44,03 | 3,508 | 12,306 | 3,785 | 13,277 | 27,478 | 72,911 | 629,564 |
| 7 | 16,22 | 13,7 | 2,786 | 7,763 | 2,617 | 7,293 | 20,234 | 1,677 | 27,446 |
| 8 | 3,88 | 9,13 | 1,356 | 1,838 | 2,212 | 2,999 | 11,033 | 62,506 | 96,214 |
| 9 | 0,75 | 3,86 | -0,288 | 0,083 | 1,351 | -0,389 | 5,496 | 180,711 | 227,373 |
| Итого | 149,3 | 170,45 | 19,029 | 55,397 | 24,511 | 58,257 | 747,465 | 1294,358 |
Для
нахождения коэффициентов степенной регрессии необходимо решить систему
уравнений:
Подставляя
в систему уравнений, получаем:
Решая
систему уравнений, получаем:
Искомое уравнение
степенной регрессии:
Коэффициент
детерминации:
Коэффициент эластичности:
Уравнение степенной модели имеет вид:
Для
построения этой модели необходимо
произвести линеаризацию переменных.
Для этого произведем логарифмирование
обеих частей уравнения:
lgŷ =lga+blgx
|
Факт |
Lg(Y) |
Переменная |
Lg(x) |
|
|
Y(t) |
X(t) |
|||
|
1 |
64.0 |
1.806 |
64 |
1.806 |
|
2 |
56.0 |
1.748 |
68 |
1.833 |
|
3 |
52.0 |
1.716 |
82 |
1.914 |
|
4 |
48.0 |
1.681 |
76 |
1.881 |
|
5 |
50.0 |
1.699 |
84 |
1.924 |
|
6 |
46.0 |
1.663 |
96 |
1.982 |
|
7 |
38.0 |
1.580 |
100 |
2.000 |
|
28 |
354 |
11.893 |
570 |
13.340 |
|
Сред.знач. |
50.5714 |
1.699 |
81.429 |
1.906 |
Обозначим
Y=lgŷ, X = lg
x, A = lg a. Тогда уравнение примет вид:
Y=A+bX- линейное уравнение регрессии.
Рассчитаем его параметры, используя
данные таблицы 3.6
Таблица 3.6
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
64 |
1,8062 |
64 |
1,8062 |
3,2623 |
3,2623 |
61.294 |
2.706 |
4.23 |
7.322 |
|
2 |
56 |
1,7482 |
68 |
1,8325 |
3,2036 |
3,3581 |
58.066 |
-2.066 |
3.69 |
4.270 |
|
3 |
52 |
1,7160 |
82 |
1,9138 |
3,2841 |
3,6627 |
49.133 |
2.867 |
5.51 |
8.220 |
|
4 |
48 |
1,6812 |
76 |
1,8808 |
3,1621 |
3,5375 |
52.580 |
-4.580 |
9.54 |
20.976 |
|
5 |
50 |
1,6990 |
84 |
1,9243 |
3,2693 |
3,7029 |
48.088 |
1.912 |
3.82 |
3.657 |
|
6 |
46 |
1,6628 |
96 |
1,9823 |
3,2960 |
3,9294 |
42.686 |
3.314 |
7.20 |
10.982 |
|
7 |
38 |
1,5798 |
100 |
2,0000 |
3,1596 |
4,0000 |
41.159 |
-3.159 |
8.31 |
9.980 |
|
итог |
354 |
11,8931 |
13,3399 |
22,6370 |
25,4528 |
0,51 |
42.32 |
65.407 |
Уравнение
регрессии будет иметь вид :
Y=3.3991-0,8921 X
Перейдем к исходным
переменным x и y, выполнив потенцирование
данного уравнения.
Получим уравнение
степенной модели регрессии:
Определим
индекс корреляции:
Связь
между показателем y
и фактором x
можно
считать достаточно сильной.
Коэффициент
детерминации:
0.836
Вариация результата
Y(объема выпуска продукции)
на 83,6 % объясняется вариацией фактора
Х (объемом капиталовложений).
РассчитаемF-критерий Фишера:
F>FТАБЛ
= 6,61 для
= 0,05. к1=m=1,
k2=n-m-1=5
Уравнение регрессии
с вероятностью 0,95 в целом статистически
значимое, т. к. F>FТАБЛ.
Средняя
относительная ошибка
.
В среднем расчетные
значения ŷ для степенной модели отличаются
от фактических значений на 6,04 %.
Соседние файлы в папке Дополнительный материал
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение нелинейной регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Виды нелинейной регрессии
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
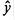
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели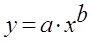 
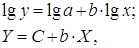
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где 
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: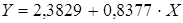 
. Выполнив его потенцирование, получим: 
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y.
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели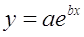 
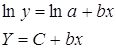
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где 
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: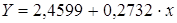 
. Выполнив его потенцирование, получим: 
Для расчета теоретических значений y подставим в уравнение 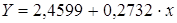значения x.
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели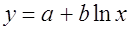 
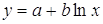
предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:
где 
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: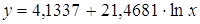 
.
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель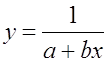 
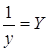
к линейному виду, заменив 
, тогда 
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: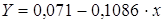 
. Выполнив его потенцирование, получим: 
Для расчета теоретических значений y подставим в уравнение 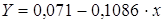значения x.
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы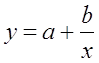 
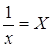
к линейному виду, заменив 
, тогда 
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: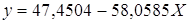 
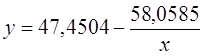
. Получим уравнение регрессии: 
.
3. Оценка тесноты связи с помощью показателей корреляции и детерминации:
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy=b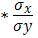
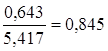
=7,122*
, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²xy=(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции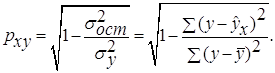 
=
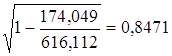
, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²xy=0,7175. Это означает, что 71,75% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy=0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy=0,66. Это означает, что 66% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy=0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,58% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy=0,8448 и коэффициент корреляции rxy=-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy=0,8114 и коэффициент корреляции rxy=-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,6584. Это означает, что 65,84% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy=0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x 2 | y 2 | ||
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
| 8,4988 | 11,1431 | х | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .
,
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x) 2 | (lg y) 2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
| 8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х | |
| 72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата . По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | ||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
| 8,4988 | 11,1431 | 0,000640820 | х | х | х | |
| 72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
http://kazedu.com/referat/102126/1
http://ecson.ru/economics/econometrics/zadacha-1.postroenie-regressii-raschyot-korrelyatsii-oshibki-approximatsii-otsenka-znachimosti-i-prognoz.html
Power regression is a type of non-linear regression that takes on the following form:
y = axb
where:
- y: The response variable
- x: The predictor variable
- a, b: The regression coefficients that describe the relationship between x and y
This type of regression is used to model situations where the response variable is equal to the predictor variable raised to a power.
The following step-by-step example shows how to perform power regression for a given dataset in R.
Step 1: Create the Data
First, let’s create some fake data for two variables: x and y.
#create data
x=1:20
y=c(1, 8, 5, 7, 6, 20, 15, 19, 23, 37, 33, 38, 49, 50, 56, 52, 70, 89, 97, 115)
Step 2: Visualize the Data
Next, let’s create a scatterplot to visualize the relationship between x and y:
#create scatterplot
plot(x, y)
From the plot we can see that there exists a clear power relationship between the two variables. Thus, it seems like a good idea to fit a power regression equation to the data instead of a linear regression model.
Step 3: Fit the Power Regression Model
Next, we’ll use the lm() function to fit a regression model to the data, specifying that R should use the log of the response variable and the log of the predictor variable when fitting the model:
#fit the model model <- lm(log(y)~ log(x)) #view the output of the model summary(model) Call: lm(formula = log(y) ~ log(x)) Residuals: Min 1Q Median 3Q Max -0.67014 -0.17190 -0.05341 0.16343 0.93186 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.15333 0.20332 0.754 0.461 log(x) 1.43439 0.08996 15.945 4.62e-12 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.3187 on 18 degrees of freedom Multiple R-squared: 0.9339, Adjusted R-squared: 0.9302 F-statistic: 254.2 on 1 and 18 DF, p-value: 4.619e-12
The overall F-value of the model is 252.1 and the corresponding p-value is extremely small (4.619e-12), which indicates that the model as a whole is useful.
Using the coefficients from the output table, we can see that the fitted power regression equation is:
ln(y) = 0.15333 + 1.43439ln(x)
Applying e to both sides, we can rewrite the equation as:
- y = e 0.15333 + 1.43439ln(x)
- y = 1.1657x1.43439
We can use this equation to predict the response variable, y, based on the value of the predictor variable, x.
For example, if x = 12, then we would predict that y would be 41.167:
y = 1.1657(12)1.43439 = 41.167
Bonus: Feel free to use this online Power Regression Calculator to automatically compute the power regression equation for a given predictor and response variable.
Additional Resources
How to Perform Multiple Linear Regression in R
How to Perform Exponential Regression in R
How to Perform Logarithmic Regression in R