Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Расчет треугольника по координатам вершин
Этот онлайн калькулятор по введенным координатам вершин вычисляет параметры треугольника: длины сторон, углы, периметр и площадь.
Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:
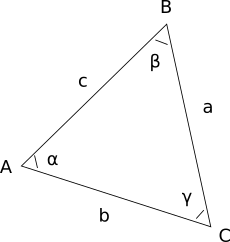
- длину стороны a — стороны, противолежащей вершине А
- длину стороны b — стороны, противолежащей вершине B
- длину стороны c — стороны, противолежащей вершине C
- значение угла α при вершине A
- значение угла β при вершине B
- значение угла γ при вершине C
- периметр треугольника
- площадь треугольника
Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором.
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
http://planetcalc.ru/9423/
http://matworld.ru/geometry/reshenie-treugolnikov.php
Уравнения сторон треугольника по координатам его вершин
A ( ; )
B ( ; )
C ( ; )
Пример решения
На этой странице можно составить онлайн уравнения сторон треугольника и
угловые коэффициенты по заданным координатам его вершин. Вставте
координаты и программа выведет подробное решение.
Калькулятор онлайн.
Решение треугольников.
Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем
данным элементам, определяющим треугольник.
Эта математическая программа находит углы ( alpha, beta ) и ( gamma ) по заданным пользователем
сторонам ( a, b ) и ( c )
Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно задать не только целые, но и дробные.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так 2.5 или так 2,5
Введите стороны a, b и c
Наши игры, головоломки, эмуляторы:
Немного теории.
Теорема синусов
Теорема
Пусть в треугольнике ABC AB = c, ВС = а, СА = b. Тогда
Стороны треугольника пропорциональны синусам противолежащих углов:
$$ frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C} $$
Теорема косинусов
Теорема
Пусть в треугольнике ABC AB = c, ВС = а, СА = b. Тогда
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное
на косинус угла между ними.
$$ a^2 = b^2+c^2-2ba cos A $$
Решение треугольников
Решением треугольника называется нахождение всех его шести элементов (т.е. трёх сторон и трёх углов) по каким-нибудь трём данным
элементам, определяющим треугольник.
Рассмотрим три задачи на решение треугольника. При этом будем пользоваться такими обозначениями для сторон треугольника ABC:
AB = c, BC = a, CA = b.
Решение треугольника по двум сторонам и углу между ними
Дано: ( a, b, angle C ). Найти ( c, angle A, angle B )
Решение
1. По теореме косинусов находим (c):
$$ c = sqrt{ a^2+b^2-2ab cos C } $$
2. Пользуясь теоремой косинусов, имеем:
$$ cos A = frac{ b^2+c^2-a^2 }{2bc} $$
По ( cos A ) находим ( angle A ) с помощью микрокалькулятора или по таблице.
3. ( angle B = 180^circ -angle A -angle C )
Решение треугольника по стороне и прилежащим к ней углам
Дано: ( a, angle B, angle C ). Найти ( angle A, b, c )
Решение
1. ( angle A = 180^circ -angle B -angle C )
2. С помощью теоремы синусов вычисляем b и c:
$$ b = a frac{sin B}{sin A}, quad c = a frac{sin C}{sin A} $$
Решение треугольника по трём сторонам
Дано: ( a, b, c ). Найти ( angle A, angle B, angle C )
Решение
1. По теореме косинусов получаем:
$$ cos A = frac{b^2+c^2-a^2}{2bc} $$
По ( cos A ) находим ( angle A ) с помощью микрокалькулятора или по таблице.
2. Аналогично находим угол B.
3. ( angle C = 180^circ -angle A -angle B )
Решение треугольника по двум сторонам и углу напротив известной стороны
Дано: ( a, b, angle A ). Найти ( c, angle B, angle C )
Решение
1. По теореме синусов находим ( sin B ) получаем:
$$ frac{a}{sin A} = frac{b}{sin B} Rightarrow sin B = frac{b}{a} cdot sin A $$
Введём обозначение: ( D = frac{b}{a} cdot sin A ). В зависимости от числа D возможны случаи:
Если D > 1, такого треугольника не существует, т.к. ( sin B ) больше 1 быть не может
Если D = 1, существует единственный ( angle B: quad sin B = 1 Rightarrow angle B = 90^circ )
Если D < 1 и a < b, то ( angle B ) имеет два возможных значения: острый ( angle B = arcsin D ) и тупой
( angle B’ = 180^circ — angle B )
Если D < 1 и ( a geqslant b), то ( angle A geqslant angle B ) (против большей стороны лежит больший угол). Т.к. в треугольнике не
может быть двух тупых углов, тупой угол для ( angle B ) исключён, и угол ( angle B = arcsin D ) единственный.
2. ( angle C = 180^circ -angle A -angle B )
3. С помощью теоремы синусов вычисляем сторону c:
$$ c = a frac{sin C}{sin A} $$
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Пример.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
Решение:
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Уравнение стороны AC —









