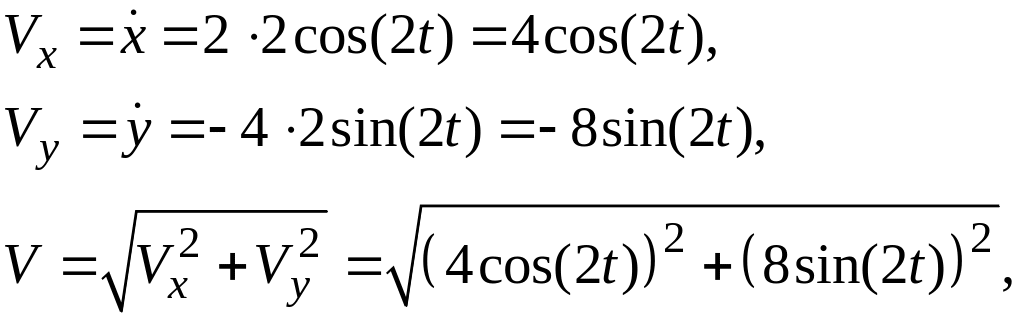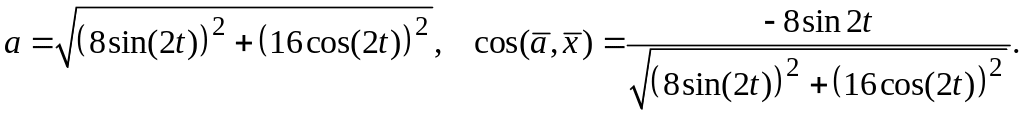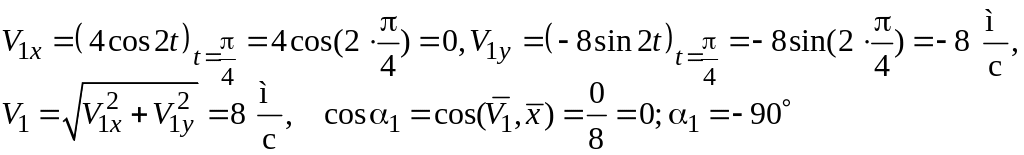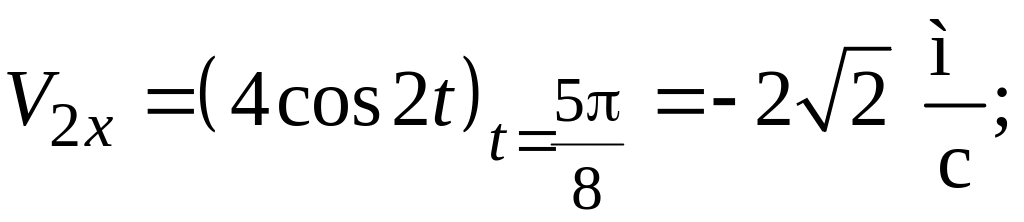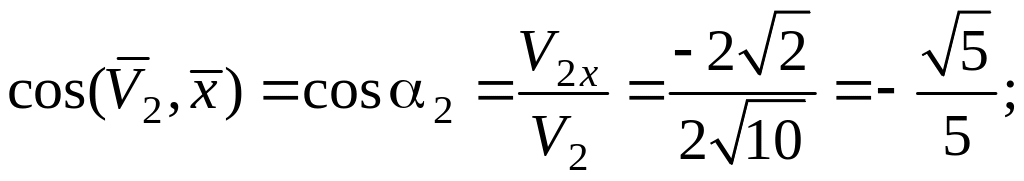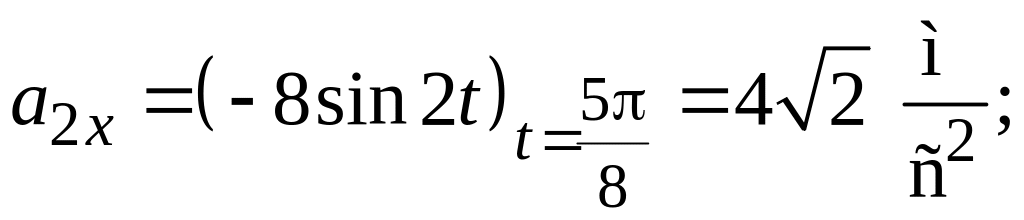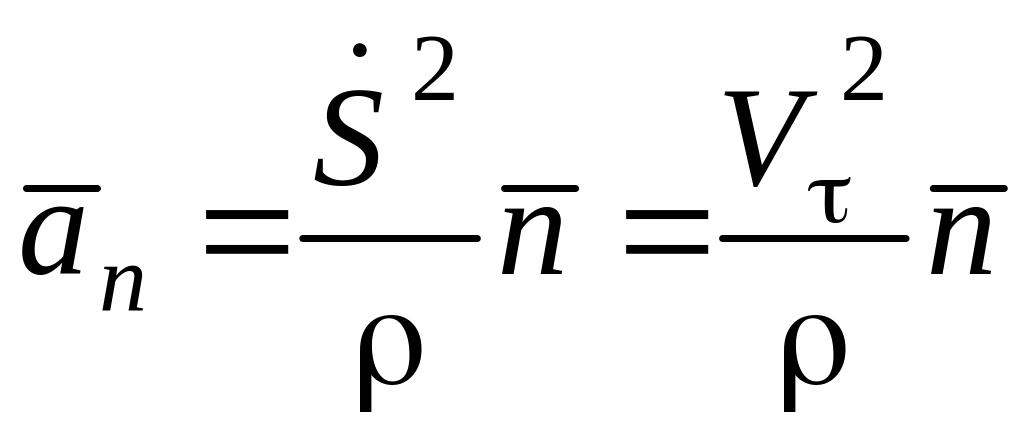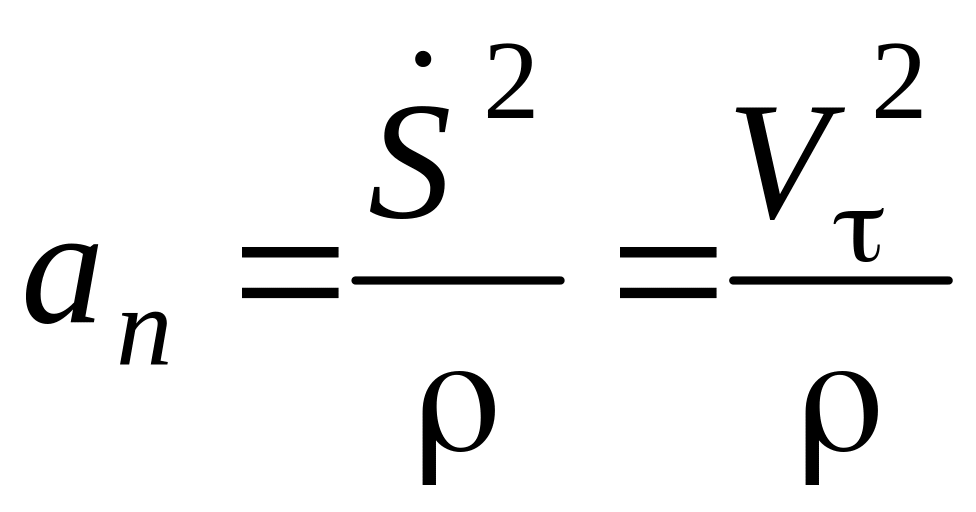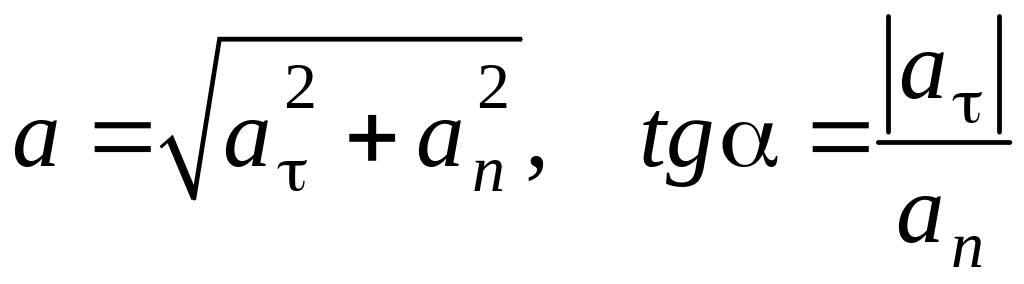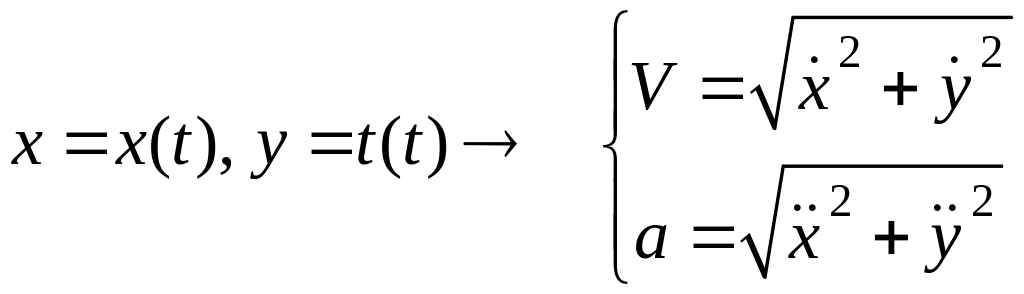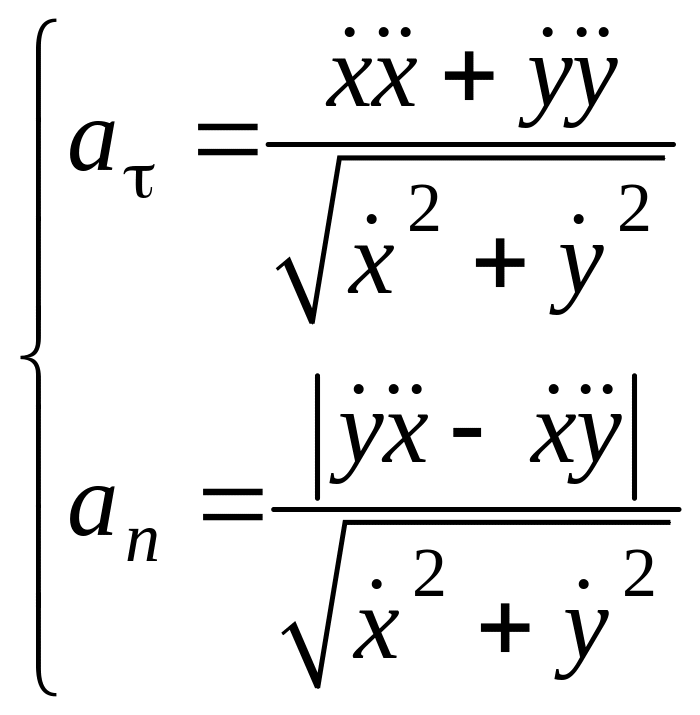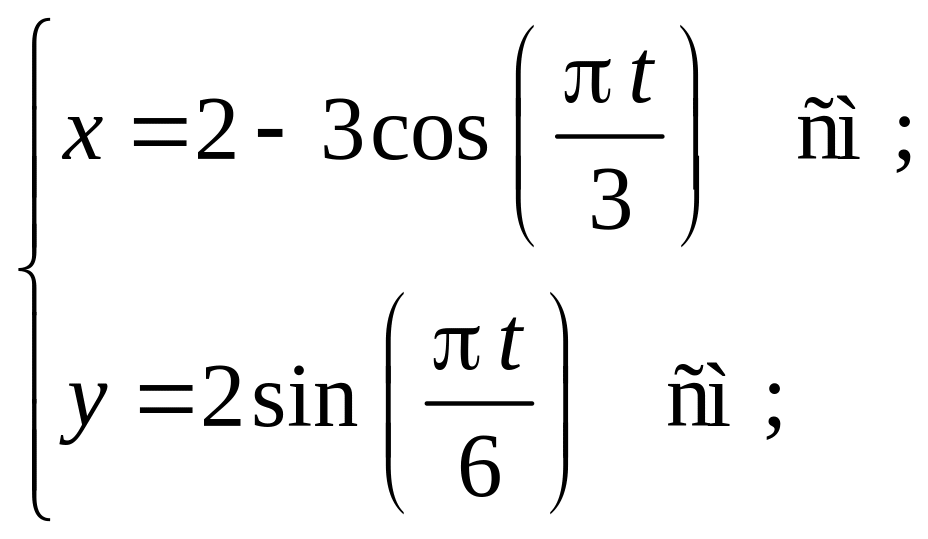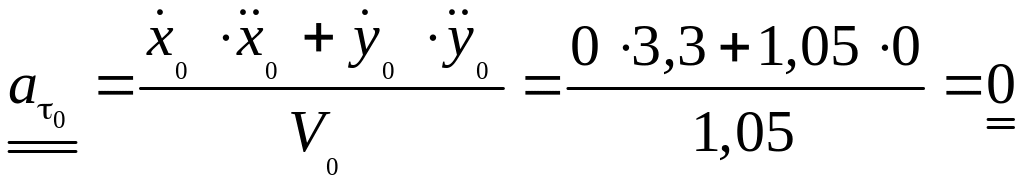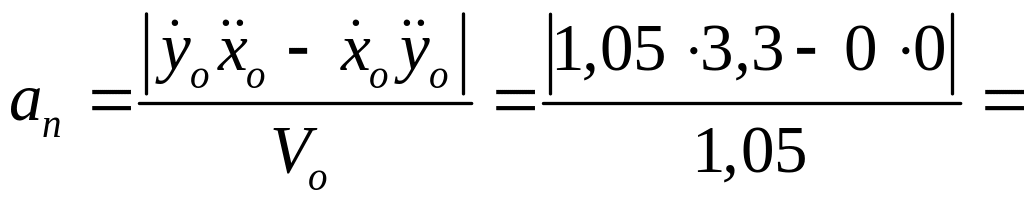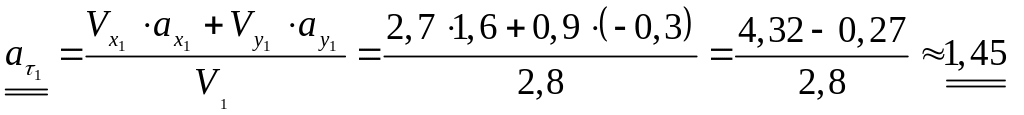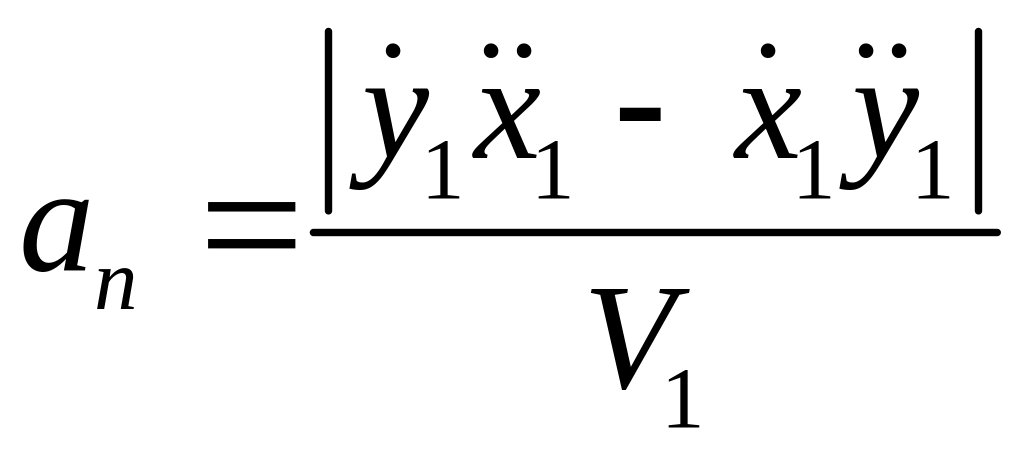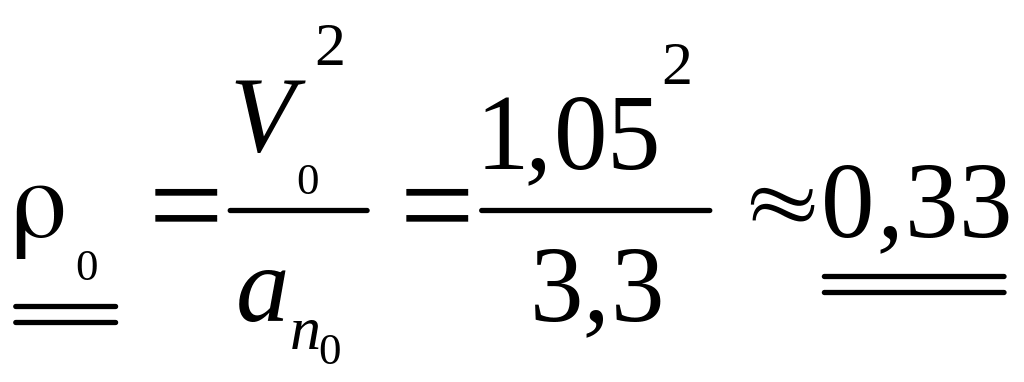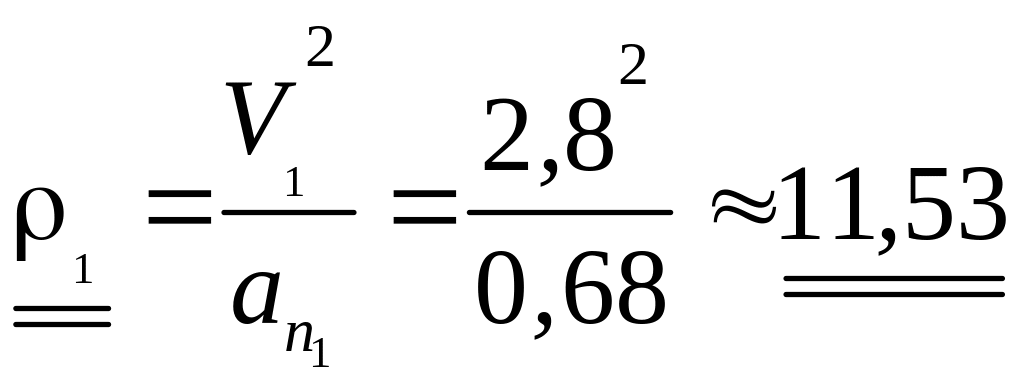Как найти уравнение траектории движения тела - Исправление недочетов и поиск решений вместе с Examum.ru

Траектория движения в физике, теория и онлайн калькуляторы

Траектория движения

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Определение

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
и криволинейное перемещение (траектория — кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

[overline{r}left(tright)={overline{r}}_0+{overline{v}}_0t+frac{overline{a}t^2}{2}left(1right),]

(где $overline{r}left(tright)$ — радиус-вектор точки в момент времени $t$; ${overline{v}}_0$ — начальная скорость движения точки; $overline{a}$ — ускорение точки,) траектория движения представляет собой плоскую кривую, что означает все точки этой кривой находятся в одной плоскости. Положение этой плоскости в пространстве задают векторы ускорения и начальной скорости. Ориентацию координатных осей чаще всего выбирают так, чтобы плоскость движения совпадала с одной из координатных плоскостей. В этом случае векторное уравнение (1) можно свести к двум скалярным уравнениям.

Уравнение траектории движения

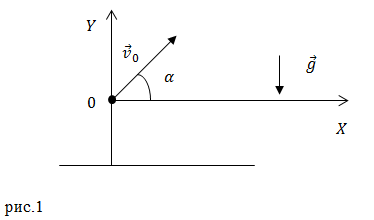
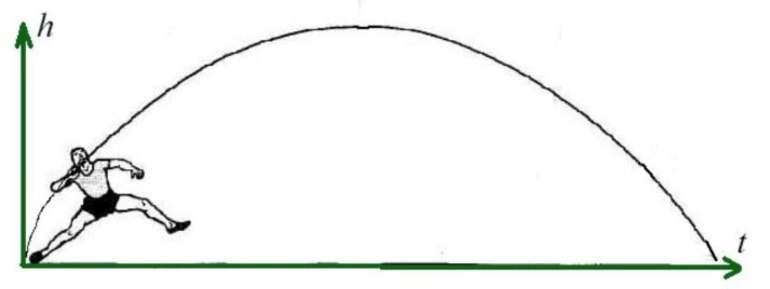
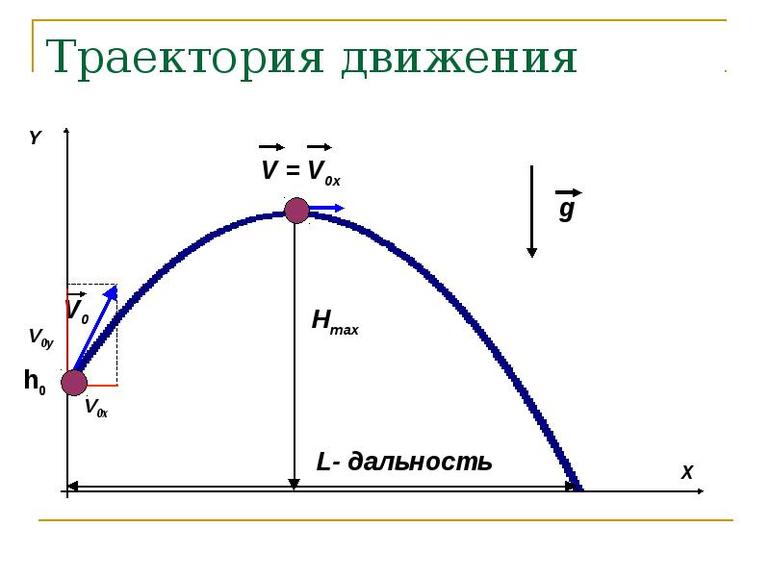
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

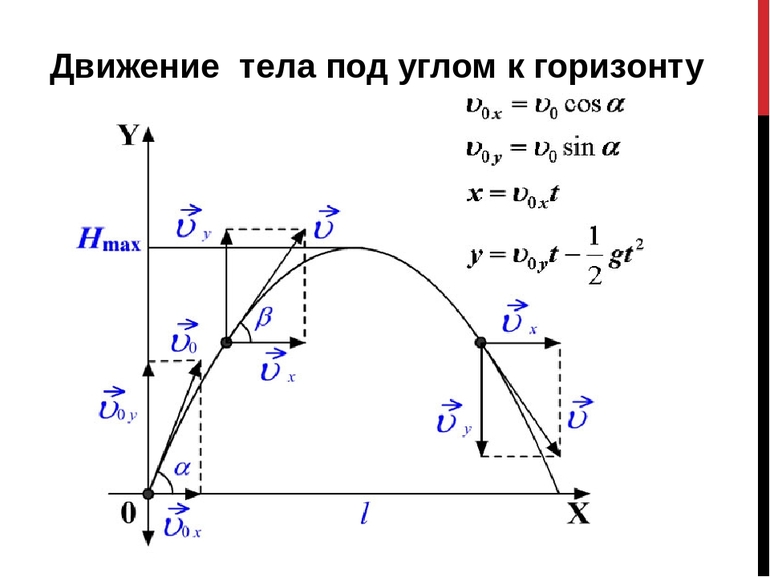
Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

[left{ begin{array}{c}
x=v_0t{cos alpha left(2right), } \
y=v_0t{sin alpha }-frac{gt^2}{2}left(3right). end{array}
right.]

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

[t=frac{x}{v_0{cos alpha }}; y=v_0frac{x}{v_0{cos alpha }}{sin alpha }-frac{g}{2}{left(frac{x}{v_0{cos alpha }}right)}^2to y=x tg alpha -frac{gx^2}{2v^2_0{cos}^2alpha }left(4right).]

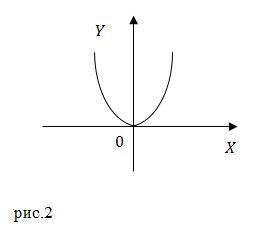
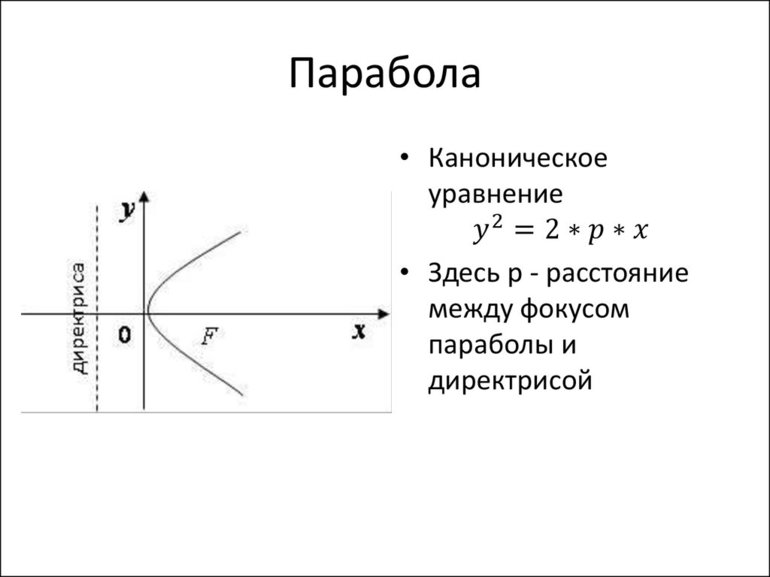
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

[left{ begin{array}{c}
x=frac{v^2_0{sin alpha {cos alpha } }}{g} \
y=frac{v^2_0{sin}^2alpha }{2g} end{array}
right.left(5right).]

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac{dy}{dx}$) от нее по $x$.

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции:

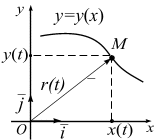
[x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]

При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline{r}$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline{r}$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение:

[overline{r}=overline{r}left(tright)left(7right).]

Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

[s=sleft(tright)left(8right).]

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

[s=Atleft(9right),]

где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Примеры задач с решением

Пример 1

Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline{v}=Aoverline{i}+Bxoverline{j} , $где $overline{i}$, $overline{j}$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit{}

Решение: Рассмотрим уравнение изменения скорости частицы:

[overline{v}=Aoverline{i}+Bxoverline{j} left(1.1right).]

Из этого уравнения следует, что:

[left{ begin{array}{c}
v_x=A, \
v_y=Bx end{array}
right.left(1.2right).]

Из (1.2) имеем:

[dx=v_xdt=Adtto dt=frac{dx}{A};;dy=v_ydt=Bxdtto dy=Bxfrac{dx}{A} left(1.3right).]

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

[y=intlimits^x_0{frac{B}{A}}xdx=frac{B}{2A}x^2.]

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

[left{ begin{array}{c}
x=0 \
y=0. end{array}
right.]

Пример 2

Задание: Движение материальной точки в плоскости описывает система уравнений: $left{ begin{array}{c}
x=At. \
y=At(1+Bt) end{array}
right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

[left{ begin{array}{c}
x=At. \
y=Atleft(1+Btright) end{array}
right.left(2.1right).]

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

[t=frac{x}{A}left(2.2right).]

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

[y=Atleft(1+Btright)=At+ABt^2=Afrac{x}{A}+AB{(frac{x}{A})}^2=x+frac{B}{A}x^2.]

Ответ: $y=x+frac{B}{A}x^2$

Читать дальше: ускорение тела.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Кинематика изучает простейшую форму движения – механическое движение. Кинематически определить движение тела – это значит указать его положение относительно выбранной системы отсчета в каждый момент времени.

Движение материальной точки (в дальнейшем будем говорить просто точки) задано, если известен закон движения.

Закон движения. Закон движения – это уравнение, позволяющее определить положение точки относительно выбранной системы отсчета в любой момент времени.

Основная задача кинематики точки. По известному закону движения определить траекторию движения точки, ее положение на траектории, скорость и ускорение точки в ее положении на траектории.

Способы задания движения точки

В зависимости от выбора системы отсчета существуют три способа задания движения точки – векторный, координатный и естественный. Рассмотрим эти способы задания движения в отдельности.

Векторный способ задания движения точки

Пусть точка движется вдоль некоторой линии. В качестве начала отсчета выберем произвольный центр . Положение точки на линии определяется радиус-вектором (рис.К.9).

Таким образом, вектор определяет положение движущейся точки в любой момент времени. Следовательно, уравнение является законом движения при векторном способе задания движения.

Величина $vec v = mathop {lim }limits_{Delta t to o} frac{{Delta vec r}}{{Delta t}} = frac{{dvec r}}{{dt}}$ называется вектором скорости точки. Вектор скорости точки всегда направлен по касательной к годографу (траектории движения точки) в сторону перемещения точки.

Величина $vec a = mathop {lim }limits_{Delta t to o} frac{{Delta vec v}}{{Delta t}} = frac{{dvec v}}{{dt}}$ называется вектором ускорения точки.

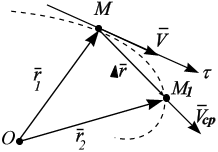
Определим направление вектора . Направление вектора vec a определяется направлением вектора . Пусть точка движется по некоторой траектории (рис.К.10) от точки ${A_1}$ к точке ${A_2}$ . Пусть скорость в точке ${A_1}$ равна ${vec v_1}$ , а скорость в точке ${A_2}$ равна ${vec v_2}$ . Перенесем вектор ${vec v_2}$ параллельно самому себе из точки ${A_2}$ в точку ${A_1}$ .

Тогда вектор $Delta vec v = {vec v_2} - {vec v_1}$ .

Как показано на рис.К.10, вектор направлен в сторону вогнутости траектории движения точки, следовательно и вектор ускорения vec a всегда направлен в ту же сторону, то есть в сторону вогнутости траектории движения точки.

Координатный способ задания движения точки

Пусть точка движется вдоль некоторой линии. В качестве системы отсчета выберем декартовую систему координат с началом в произвольном центре . Тогда положение точки на линии определяются текущими координатами в любой момент времени $left{ begin{array}{l} x = x(t)\ y = y(t) end{array} right.$

Следовательно, система уравнений $left{ begin{array}{l} x = x(t)\ y = y(t) end{array} right.$ определяют закон движения точки при координатном способе задания движения. Исключая из закона движения время , получим уравнение вида , являющееся уравнением траектории движения точки.

Пример. Закон движения записывается уравнениями $left{ begin{array}{l} x = 5t + 5\ y = 6t + 7 end{array} right.$ . Найти уравнение траектории движения точки.

Решение. Из первого уравнения следует, что или $(t + 1) = frac{x}{5}$ . Тогда из второго уравнения $y = 6(t + 1) + 1 = frac{6}{5}x + 1$ . Или $y = frac{6}{5}x + 1$ . Таким образом получено, что траекторией движения точки является прямая линия $y = frac{6}{5}x + 1$ .

Компоненты скорости и ускорения движущейся точки в любой момент времени определяются по формулам

${v_x} = frac{{dx(t)}}{{dt}} = dot x(t)$

${a_x} = {dot v_x} = ddot x(t)$

${v_y} = frac{{dy(t)}}{{dt}} = dot y(t)$

${a_y} = {dot v_y} = ddot y(t)$ (К.9)

Модули скорости и ускорения $v = sqrt {v_x^2 + v_y^2}$

$a = sqrt {a_x^2 + a_y^2}$ (К.10)

Векторы скорости и ускорения

$vec v = {v_x}vec i + {v_y}vec j$

$vec a = {a_x}vec i + {a_y}vec j$ .

Источник

Кинематика

2.1. Траектория, скорость, ускорение материальной точки

Траектория
точки.
Геометрическое
место последовательных положений
движущейся точки называется ее
траекторией.
Если в интервале времени

траектория 
прямая линия, то движение в этом интервале
называется прямолинейным,
в противном случае движение называется
криволинейным.

Рис.
2.1

корость точки.
Пусть
положение движущейся точки М
относительно произвольно выбранного
неподвижного центра О
определяется в момент времени t
радиус-вектором

,
который соединяет движущуюся точку М
с центром О
(рис.
2.1).

За
время

радиус-вектор изменится на

.

Мгновенная
скорость точки

в момент времени t
определяется как предел средней скорости
при t
→ 0,
т. е.

.
(2.1)

Производная
по времени от функций обозначается
точкой над символом этой функции, а
вторая производная – двумя точками.

Вектор
скорости приложен в точке М,
направлен в сторону ее движения по
предельному направлению вектора

→
0, т. е. совпадает
с касательной к траектории в точке М.
Размерность скорости в СИ:

= длина/время = м/с. Часто скорость выражают
в км/ч = 0,28 м/с.

Скорость
–
это
векторная величина, характеризующая
быстроту и направление движения точки

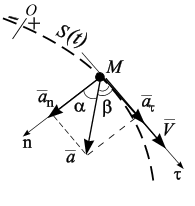
Ускорение
точки. Пусть
движущаяся точка М
в момент времени t
имеет скорость

(рис.
2.2). В момент времени

=
t + Δt
эта точка занимает положение

,
имея скорость

.
Чтобы изобразить приращение скорости

за время Δt,
перенесем вектор скорости

параллельно самому себе в точку М,
тогда

.

Ускорением
точки

в момент времени t
называют предел, к которому стремится
среднее ускорение при Δt
→ 0, т. е.

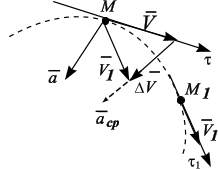
Рис.
2.2

. (2.2)

Вектор
ускорения

всегда направлен внутрь вогнутости под
любым углом к касательной к траектории
движения (рис. 2.2). Размерность ускорения
в СИ:

= длина/время²
= м/с².

Ускорение – это векторная
величина, характеризующая быстроту

изменения
модуля и направления вектора скорости.

Движение
точки на плоскости

Рис.
2.3

Рис.
2.5

оординатный способ задания движения
точки. Зададим радиус-вектор

в декартовой системе координат
Оху:

Тогда
движение точки можно задать уравнениями

(2.3)

Уравнения
(2.3) являются уравнениями движения точки,
а также уравнениями траектории точки,
заданными параметрически. Уравнение
траектории в системе координат

будет иметь вид функции

(рис. 2.3). Для получения этой зависимости
следует из уравнений (2.3) исключить
параметр

_.Уравнение
траектории в явном виде будет иметь вид
функции

Скорость
и ускорение точки по модулю и направлению
вычисляются по формулам:

;

Содержание
контрольных работ для студентов на тему
«кинематика точки» дано в приложении
(контрольная работа 1, задача 1).

Пример
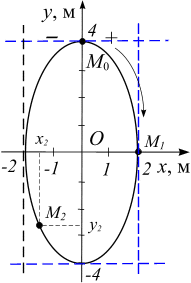
2.1. Движение
точки M
по плоскости Оху
задано уравнениями движения

.
(а)

Значения
х и
у – в
метрах. Построить траекторию движущейся
точки, вычислить скорость и ускорение
точки в моменты времени

и

.

Решение.
Для
построения
траектории движущейся точки в декартовой
системе координат определим область,
в которой движется точка, т. е. область
значений

и

.^¹
Так как

и

,
получаем:

Выделяем
область, ограниченную полученными
неравенствами, за эту область точка при
движении не выходит (рис. 2.4) Исключим
параметр t
из
уравнений движения (a).
Для этого делим первое уравнение на 2,
второе – на 4, возводим их в квадрат и
складываем между собой:

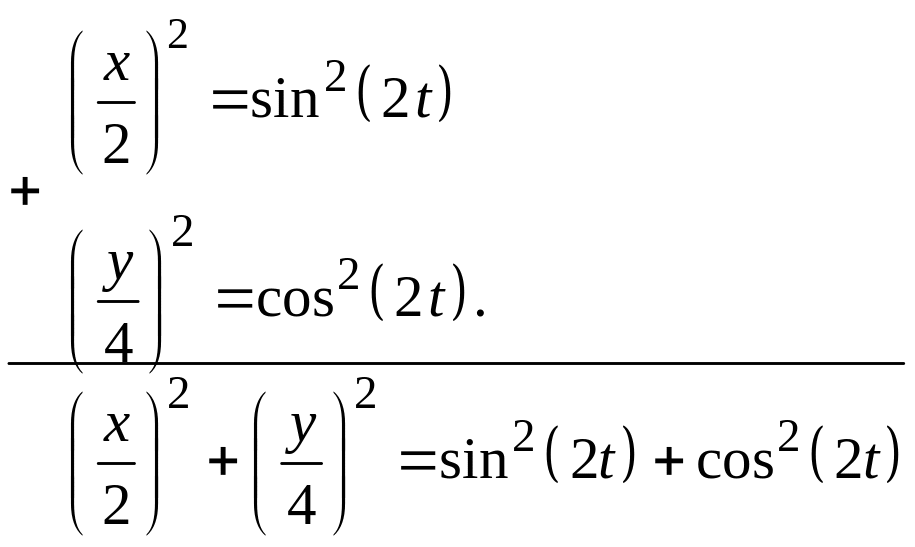
Учитывая,
что

,
получим:

. (б)

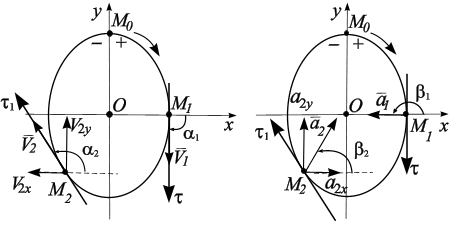
Траекторией
движущейся точки является эллипс (рис.
2.4). Подставляя в (а) значение

,
находим:

;

м.

Точка
в начальный момент времени занимает
положение

.

_{Определим

направление движения точки. Уравнения

движения (а) заданы возрастающей функцией}

и убывающей функцией

,
поэтому при увеличении t
координата «х» возрастает, а «у»
убывает, следовательно, точка движется
по эллипсу по часовой стрелке.

Р
ис.2.4

Определим
модуль и направление вектора скорости
точки М.
Имеем:

(в)

Определим
модуль и направление вектора ускорения
точки М.
Имеем:

(г)

При

из (а) получаем, что точка М
имеет координаты х₁
= 2,

у₁
= 0, т. е.
занимает положение (рис. 2.4) М₁.
Подставляя в (в) и (г) время

,
получим

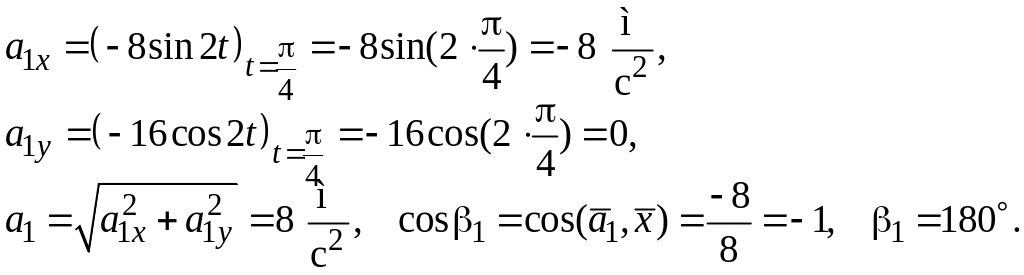
Откладываем
значение скорости (рис. 2.5, а)
и ускорения (рис. 2.5, б)
точки М₁на траектории.

При

из (а) получаем, координаты точки

:

Вычислим, используя
(в) и (г), модуль и направление векторов
скорости и ускорения.


а	б
Рис. 2.5

Имеем:

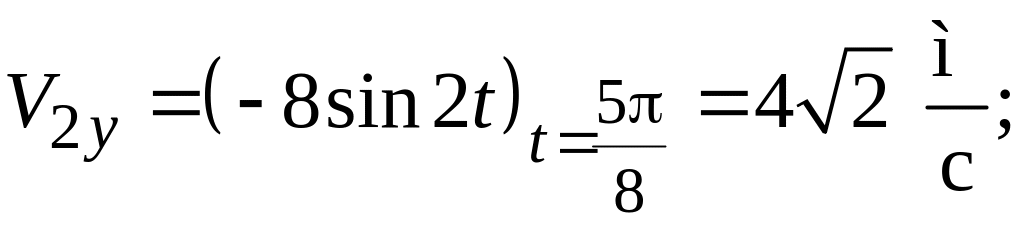
для
ускорения

,

.

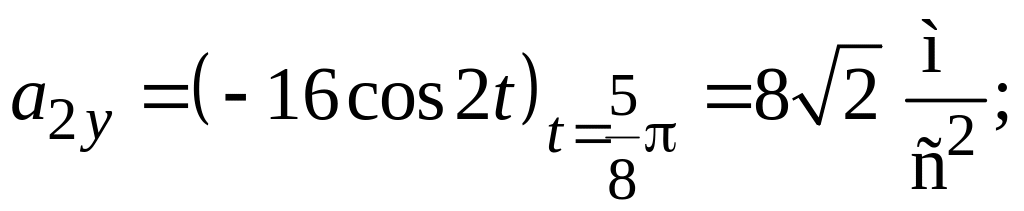
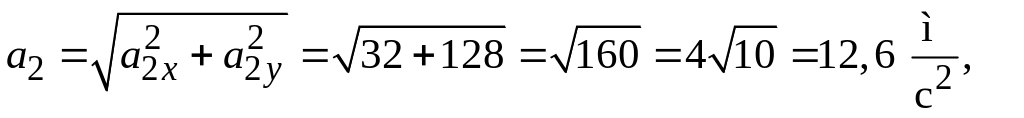
Откладываем
значение скорости (рис. 2.5, а)
и ускорения (рис. 2.5, б)
точки

на
траектории.

Вектор
скорости точки совпадает по направлению
с касательной к траектории в точках

,
а вектор ускорения в точках

направлен во внутрь вогнутости траектории
(к центру О).

Ответ:
V₁=
8 м/с,
a₁=
8 м/с²;
V₂=
6,3 м/с, a₂=
12,6 м/с².

Естественный
способ задания движения точки.

Р
ис.
2.6

При
естественном способе задания движения
точки задаются (рис. 2.6):

– траектория
движения точки;

– начало
и направление увеличения дуговой
координаты

;

– уравнение
движения точки по траектории, как
функция времени:

где
S
– дуговая координата, отчитываемая
от начала движения.

Примером
естественного способа задания движения
является движение поезда: траектория
и направление движения определены
рельсами, а уравнение движения задано
таблицей – расписанием движения поезда.

Движение
точки рассматривается в координатах

.
Единичный вектор

направлен по вектору скорости, единичный
вектор

перпендикулярен вектору

,
направлен по главной нормали кривой в
сторону ее вогнутости (рис. 2.6).

Скорость
точки

направлена по касательной и равна

Ускорение

точки

при
естественном способе задания движения
раскладывается на два – касательное
ускорение

,
и нормальное ускорение

:

Касательное
ускорение

характеризует изменение величины
скорости, нормальное

– изменение направления вектора
скорости.

Естественный
способ задания движения это:

+
траектория

– касательное
ускорение;

– нормальное
ускорение;

Связь координатного
и естественного способов заданий
движения точки

Рис. 2.7

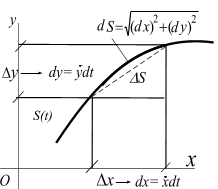
Известно,
что если
точка движется в плоскости О
,
элемент дуги

связан
с приращениями координат теоремой
Пифагора (рис. 2.7):

При

имеем

тогда
дифференциал дуги

связан с дифференциалами функций

(рис.2.7):

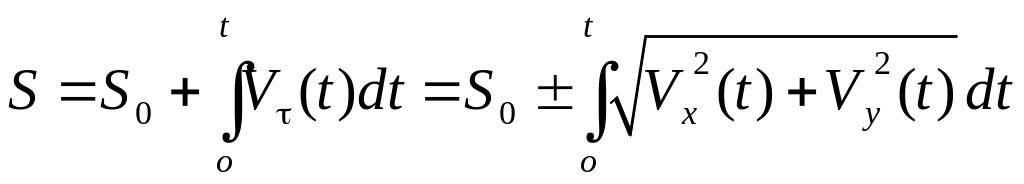
(знак
+ или 
совпадает со знаком

,
так как

).

Пример
2.2.

Точка
движется в плоскости

.
Уравнение движения точки задано
координатами

,

,
где

выражены в см,


в с.

Исходные
данные:

(см);

(см).

Требуется:

Записать
уравнение траектории в явном виде:

(или

).
Построить
траекторию.
Определить
положение точки в начальный момент
времени

и момент времени

с, направление движения точки по
траектории.
Вычислить
вектор скорости

и вектор ускорения

точки в начальный (
)
и конечный (

с) моменты времени.
Задать
движение точки естественным способом
(вывести закон

).
Геометрически
и аналитически определить нормальную

и касательную

составляющие ускорения точки в начальный
и конечный моменты времени.
Найти
радиус кривизны траектории в начальный
и конечный моменты времени.

Решение

Выводим
уравнение траектории в явном виде.

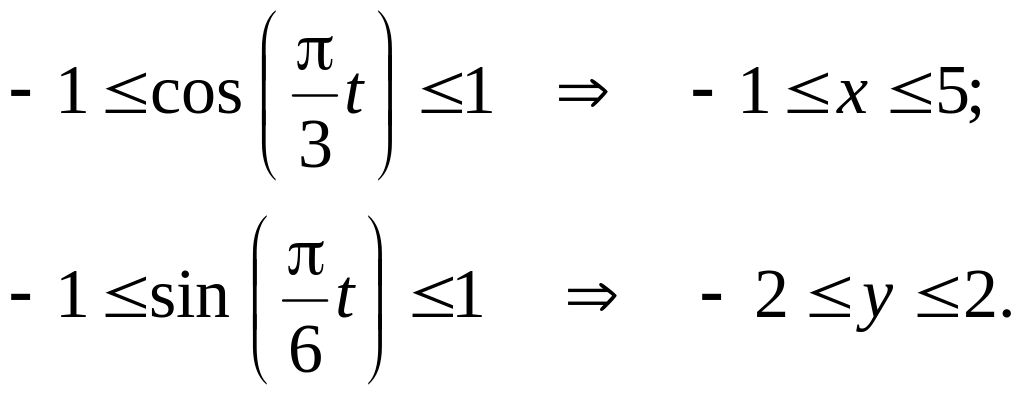
Из
первого уравнения системы:

;
из второго уравнения системы:

.
Получаем:

;

,
или

.

Таким
образом, получаем уравнение параболы

Строим
траекторию в масштабе

(рис. 2.8).

Ветви
параболы вытянуты вдоль оси

.
Вершина параболы:

;

см

С (−1;0).

, см	± 1	± 2
, см	0,5	5

Определяем
положение точки в заданные моменты
времени.

;

М₀
(−1; 0);

с;

М₁
(0,5; 1).

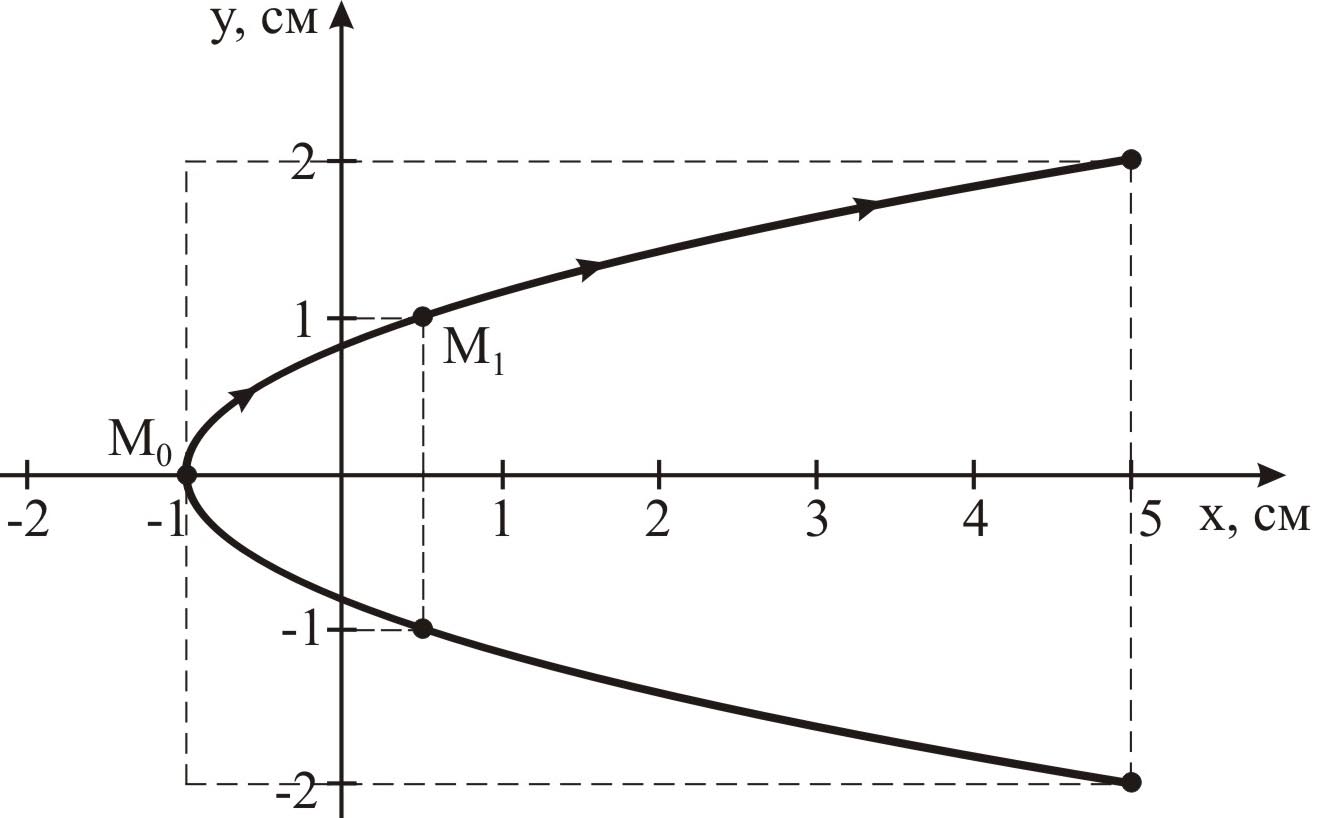
Рис. 2.8

Направление
движения точки по траектории в промежуток
времени от

с до

с определяем по уравнениям движения

и

:

– функция
убывающая, но она в выражении со знаком

«–», значит, координата

возрастает;
– функция
возрастающая, значит, координата

возрастает.

Таким
образом, движение точки по параболе в
указанный промежуток времени происходит
по часовой стрелке (по верхней ветви
параболы) (рис. 2.8).

В
целом, точка совершает колебательные
движения по построенной параболе в
области, указанной пунктиром на графике
(рис. 2.8).

Вычисляем
скорость и ускорение для заданных
моментов времени.

Так
как движение точки задано координатным
способом, то скорость

и ускорение

определяются по их проекциям на
координатные оси (рис. 2.9).

Скорость

см/с;

;

см/с;

с;

см/с;

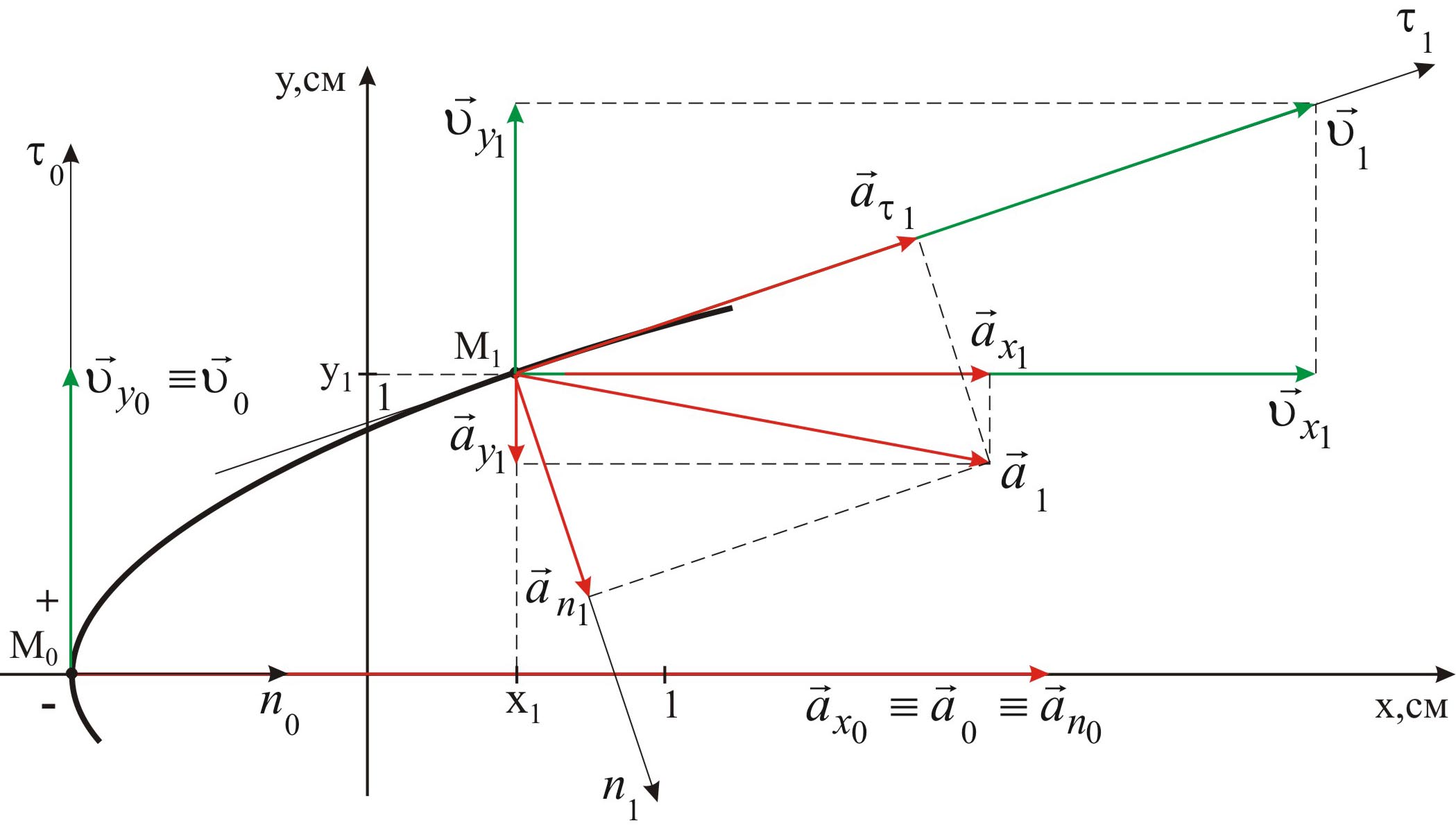
Рис. 2.9

Масштабы:
чертежа в 1 см 
0,5 см; скоростей в 1 см 
0,233 см/с; ускорений в 1 см 
0,236 см/с².

Ускорение

см/с²;

;

см/с²;

с;

см/с²;

см/с².

Выводим
закон движения точки в естественной
форме, имеем:

Для
промежутка времени от

с до

с имеем:

;

=
=

,
см.

Вычисляем
нормальное и касательное ускорения.

а)
Аналитически:

;

см/с²;

с;

см/с²,

см/с².

Так
как

,

,
движение точки в момент времени

с ускоренное.

б)
Графическое решение предполагает
выполнение геометрического равенства

для
соответствующего момента времени (рис.
2.9).

Вычисляем
радиус кривизны траектории.

Из
формулы

получаем для каждого времени

;

см;

с;

см.

Ответ:

см	см/с

−1	0	0,5	1	0	1,05	1,05	2,7	0,9	2,8

см/с²

3,3	0	3,3	1,6	−0,3	1,6

см/с²	см

граф.	анал.	граф.	анал.	граф.	анал.	граф.	анал.
0	0	3,3	3,3	1,45	1,45	0,68	0,68	0,33	11,53

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Кинематика. Механическое движение. Система отсчета. Материальная точка. Траектория. Путь

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Сегодня мы поговорим о систематическом изучении физики и первом ее разделе – механике. Физика изучает разные виды изменений или процессов, происходящих в природе, а какие процессы в первую очередь интересовали наших предков? Конечно, это процессы, связанные с движением. Им было интересно, долетит ли копье, которое они бросили, и попадет ли оно в мамонта; им было интересно, успеет ли гонец с важной вестью добежать до заката к соседней пещере. Все эти виды движения и вообще механическое движение как раз и изучает раздел, который называется механика.

Уравнение траектории тела — определение и формулы

Общие сведения

Под движением тела понимают процесс его перемещения из одной точки пространства в другую. Произошедшее действие исследуют относительно другого объекта или выбранных начальных координат. При этом положение вовсе не обязательно может изменяться сразу ко всем окружающим его телам. Например, стоящий человек на Земле находится в состоянии покоя по отношению к планете, но движется относительно Солнца.

В физике принято любое изменение определять в системе пространственных координат. За оси принимают перпендикулярные линии x, y, z. Совокупность данных, используемых для изучения движения, называют системой отсчёта.

Существует несколько видов механического перемещения (во времени) физической точки:

равномерное и равноускоренно прямолинейное;
по дуге;
гармоническое колебание.

При движении тело проходит определённый путь. Описать его можно виртуальной линией, при этом она может быть как прямой, так и кривой. Именно она и называется траекторией движения. По сути, эта линия соединяет последовательно все положения точки в пространстве — от начальной до конечной. Длина отрезка является пройденным путём и считается векторной величиной.

Изменение радиус-вектора r (значения, задающего положение точки в пространстве относительно другого тела) описывает кинематический закон: r = r (t). В трёхмерных декартовых координатах его можно записать так: r = xe + ye + ze = (x, y, z). Вектор, построенный из начальной точки движущегося тела в расположение её в данный момент времени, то есть приращение радиус-вектора за определённый промежуток t, как раз и называют перемещением.

Результирующее движение же равно векторной сумме последовательных изменений положения. При прямолинейном перемещении вектор пути совпадает с соответствующим участком траектории, а модуль перестановки равняется пройденному расстоянию.

Время, за которое тело пройдёт по установленной траектории пути, называют скоростью. Фактически это быстрота изменения координаты. Физики, исследуя передвижение, изучают не только положение материальной точки в начальный и конечный момент времени, но и закон, по которому происходит перемещение. Другими словами, они определяют зависимость радиус-вектора от времени.

Горизонтальное перемещение

Пусть имеется тело, брошенное горизонтально поверхности. Высота падения равняется h, а начальная скорость V0. Здесь систему отсчёта удобно связать с Землёй. Объект будет передвигаться под действием силы тяжести. Остальными силами, например, сопротивлением воздуха, можно пренебречь. Тело перемещается в плоскости, содержащей вектора ускорения и свободного падения (g).

Таким образом, система начальных условий будет выглядеть так: x (t = 0) = 0; y (t = 0) = 0; v0x = v0; voy = 0. Вектор ускорения постоянный, поэтому a = g. Если тело представить как совокупность материальных точек, движущихся по одинаковому пути, то путь можно определить как сумму перемещений по прямым. Уравнение скорости примет вид: v (t) = v0 + gt. Об изменении положения можно сказать, что оно выполняется с постоянной скоростью и ускорением в горизонтальной плоскости, являясь равномерным. Значит, проекцию на оси ординаты и абсциссы можно записать как vx = v0; vy = -gt.

Скорость перемещения рассчитывают по формуле: V = √‎(V 2 x + V 2 y). После подстановки полученных ранее выражений равенство примет вид: V = √‎(V 2 0 + g 2 t 2 ). Отсюда следует, что уравнение для вектора движения материальной точки будет: s (t) = s0 + V0t + (g t 2 ) / 2, где: s0 — смещение тела, соответствующее начальному моменту времени.

Так как s0 = y (t = 0) = h0, то скалярные выражения для координат изменяющей положение частицы можно представить в виде системы: x = V0t; y = h0 — (gt 2 / 2). Перемещение происходит по прямой как отдельное движение в двух плоскостях, при этом из формулы следует, что изменение положения будет соответствовать правой половине направленной вниз параболы. Учитывая то, что время можно определить из отношения икса к начальной скорости (t = x /V0), можно записать окончательную формулу для вычисления траектории движения тела: y = h0 — (gx 2 ) / (2 2 V0) .

Можно сделать вывод, что уравнение траектории не записывается через время, поэтому частица будет и перемещаться обратно по той же самой траектории. Временные отрезки между точками пути будут одинаковы как при прямом, так и при обратном движении.

Каждому положению соответствует определённое значение скорости, которое не зависит от направления перемещения. Нужно отметить, что наибольшей величиной в горизонтальной траектории полёта будет начальная точка.

Движение тела под углом

Свободное падение является частным случаем равноускоренного, то есть на перемещаемый объект действует только сила притяжения. Если физическая точка перемещается, то кривая, которая описывается её радиус-вектором, обозначает пройденный путь. Эту траекторию можно описать некоторой математической функцией.

Итак, вектор скорости точки определяется как производная по времени: V = dr / dt = r. Ускорение же можно найти, продифференцировав скорость: a = dV / dt = d 2 r / dt. Если обозначить производную времени точкой, то формулу можно переписать так: a = V = r.

Для того чтобы вывести формулу, нужно воспользоваться основными выражениями, определяющими проекции:

ускорения: ax = 0, ay = — g, az = 0;
радиус-вектора: rx (t) = V0 * cosat, ry (t) = v * sin (at — (g * t2)/2)), rz (t) = 0;
скорости: vx (t) = V0 * cosa, vy (t) = V0 * sin (a — gt), vz (t) = 0.

Чтобы запись зависимости вертикальной оси от горизонтальной была как можно более компактной, соответствующие координаты rx и ry можно обозначить через икс и игрек. Из уравнения, связывающего координатную ось X и время, можно определить t как функцию ординаты. Линейное выражение будет иметь вид: t = x / (Vo * cosa).

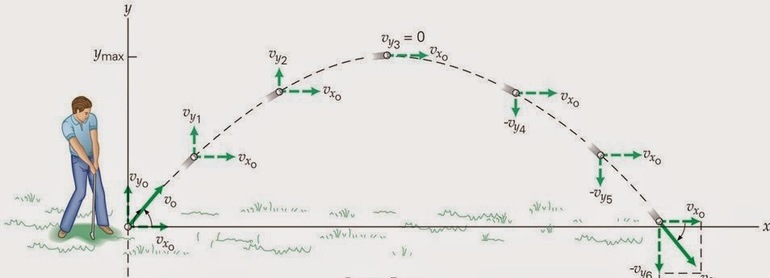
Если полученную формулу для времени подставить в уравнение для игрек координаты, то вместо временного параметра появится икс. То есть можно будет вывести зависимость абсциссы от ординаты: y = V 0 * sinat — (g * t 2 ) / 2 = (tga) * x — (g / 2 * V0 * cos 2 a) * x 2 . Значение t нужно подставить в каждое слагаемое, но при этом учесть, что отношение синуса к косинусу называют тангенсом. Альфа в формуле — это угол между направлением начальной скорости и горизонтальным направлением (угол броска). После исключения времени из этих уравнений получим уравнение траектории.

В итоге останется два слагаемых. Первое будет линейно по иксу, а второе квадратично. Таким образом, зависимость игрека от икса в уравнении траектории — это парабола (справа стоит квадратичная функция). Она проходит через начало координат. Если верно равенство x = 0, то игрек тоже будет равняться нулю.

Следует обратить внимание на то, что в квадрате стоит отрицательный коэффициент. Известно, что если перед квадратичным слагаемым в уравнении параболы стоит отрицательное число, то концы кривой будут направлены вниз.

Решение задач

Решение практических заданий лучше всего помогает закрепить полученные знания. Существуют физические сборники, которые интересны тем, что включают в себя различные примеры, приближенные к реалистичным задачам. Прорешивая их самостоятельно, ученик не только лучше разберётся в теме, но и научится применять полученные знания на практике.

Вот два таких задания:

Пусть имеется тело, движение которого описывается равенствами: x = Vx * t; y = y0 + Vy * t. Нужно определить траекторию его перемещения, учитывая, что Vx = 20 см/с, Vy = 2 м/с, Yo = 0,2 м. Для решения задачи нужно записать систему, определяемую исходными данными. Затем из первого равенства выразить время: t = x / Vx. Полученную формулу можно подставить в выражение нахождения координат абсциссы: y = y0 + (Vy * x) / Vx. Если теперь использовать исходные данные, то уравнение, описывающее траекторию, примет вид: y = 0.2 + 4x. Равенство напоминает собой формулу прямой: y = k * x + b. Исходя из этого можно утверждать, что траектория пути также будет представлять собой прямую линию. Действительно, в этом можно убедиться, если построить график движения. Для этого нужно взять несколько произвольных значений для икса, подставить их в формулу и найти вторую координату.
Следующая задача довольно интересная. Нужно составить траекторию движения для тела, движущегося равномерно со скоростью два метра в секунду, при отклонении пути от оси икс на 60 градусов. За начало координат нужно принять точку (0, 0). Тогда начальный радиус-вектор тоже будет равен нулю: R = 0. Для успешного решения примера понадобится вспомнить скалярные уравнения для проекции при равномерном движении. Так как по условию вектор задан, то можно найти его проекцию на ось игрек: Vx = v * cos60 = 1; Vy = v * cos30 = √‎3. Отсюда: x = Vx * t = t; y = Vy * t = √‎3t.

Таким образом, чтобы успешно решать задачи, нужно знать несколько основных формул для определения местоположения тела, а также то, как выглядят уравнения параболы и прямой.

Стоит отметить, что существующие онлайн-калькуляторы не умеют вычислять формулы, описывающие траекторию пути. Но вместе с тем их можно использовать для выполнения расчётов или как справочники.

Траектория движения

Определение и основные понятия траектории движения

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
и криволинейное перемещение (траектория — кривая линия).

При движении точки с постоянным ускорением, которое описывает уравнение:

Уравнение траектории движения

Вершина этой параболы находится в точке с координатами:

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Параметры траектории движения

Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit<>

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

источники:

http://nauka.club/fizika/formula-uravneniya-traektorii-tela-dvizhushchegosya-pod-uglom.html

http://www.webmath.ru/poleznoe/fizika/fizika_95_traektorija_dvizhenija.php

Источник