По этой ссылке вы найдёте полный курс лекций по математике:
Определение. Если в каждой точке M(x,y,z) пространства или части пространства определена векторная величина то говорят, что там задано векторное поле а. Задание векторного поля равносильно заданию ipex скалярных функций от трех переменных , Примерами векторных полей могут служить: силовое поле — поле некоторой силы F, поле скоростей v течения некоторой жидкости и др.
Для геометрической характеристики векторного поля служат векторные линии. Векторной линией векторного поля а называется кривая, касательная к которой в любой точке М имеет то же направление, что и вектор поля а в этой точке (рис. 7). В силовом поле векторные линии называются силовыми линиями’, в поле скоростей дви-женияжидкости векторные линии называются линиями тока. Рис. 7 3.1.
Дифференциальные уравнения векторных линий Пусть векторное поле определяется вектор-функцией ) — непрерывные функции переменных x, у, z, имеющие ограниченные частные производные первого порядка. Пусть — есть радиус-вектор текущей точки векторной линии векторного поля a (t — параметр). Из определения векторной линии следует, что вектор и вектор касательной к этой кривой должны быть коллинеарны в каждой точке векторной линии. Условием коллинеарности векторов является пропорциональность их координат:
Векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток вектора через поверхность и его свойства Свойства потока вектора через поверхность Понятие ориентации поверхности Таким образом, мы получили для векторных линий систему дифференциальных уравнений в симметричной форме. Допустим, что нам удалось найти два независимых интеграла системы (2): . Система уравнений (3) определяет векторную линию как линию пересечения двух поверхностей. Произвольно меняя параметры с, и Сг, мы получаем семейство векторных линий как семейство с двумя степенями свободы.
Пример 1. Найти векторные линии векторного поля 4 Выписываем дифференциальные уравнения векторных линий, или Интегрируя эту систему, получим два уравнения — произвольные постоянные. Пересечение плоскостей у — Сх с параболическими цилиндрами дает двух параметрическое семейство векторных линий поля (рис.8). Олредрм*т . Векторное поле называется плоским, если все векторы а параллельны одной и той же плоскости и в каждой плоскости, параллельной указан ной, векторное поле одно и то же.
Посмотрим, как плоское векторное поле описывается в координатах.
Если указанную в определении плоскость (или любую ей параллельную) принять за плоскость хОу, то векторы плоского поля не будут содержать компоненты по оси Oz и координаты векторов не будут зависеть от z: Дифференциальные уравнения векторныхл иний плоского поля можно записать в следующем виде Отсюда видно, что векторные линии плоского поля являются плоскими кривыми, лежащими в плоскостях, параллельных плоскости хОу.
Возможно вам будут полезны данные страницы:
Пример 2. Найти векторные линии магнитного поля бесконечно длинного прямого провода. ^ Предположим, что проводник направлен вдоль оси Oz и по нему течет ток силы J, т.е. вектор тока Тогда вектор напряженности Н магнитного поля определяется по формуле — радиус-вектор точхи М, р — расстояние от оси провода до точки М. Раскрывая векторное произведение (6), получим Дифференциальные уравнения векторных линий: Отсюда х = const, = или . Окончательно имеем т.е. векторные линии являются офужносгями с центрами на оси О г (рис.9). Пример 3.
Найти векторные линии поля сил тяготения, образованного притягивающей материальной то*«ой массы ш, расположенной в начале координат. Дифференциальные уравнения векторных линий: стсуда, умножая каждую из дробей на , получим Чтобы получить уравнения векторных линий в параметрической форме, приравняем каждую из дробей величине у. Имеем Это — полупрямые, выходящие из начала координат. Чтобы из семейства векторных линий выделить одну, надо задать точку ), через которую эта векторная линия должна проходить, и по координатам заданной точки определить величины.
Пусть, например, точка А/о имеет координаты . Уравнение векторной линии, проходящей через точку, можно записать так: . Сама точка Л/о получается при значении параметра § 4. Поток вектора через поверхность и его свойства Рассмотрим сначала частный случай поля скоростей v течения жидкости. Выделим в поле некоторую поверхность Потоком жидкости через поверхность Е называется количество жидкости, протекающее через поверхность Е за единицу времени.
Этот поток легко вычислить
если скорость течения постоянна (v = const), а поверхность £ —плоская. В этом случае поток жидкости равен объему цилиндрического тела с параллельными основаниями и образующими длины |v|, так как за единицу времени кажд ая частица перемещается на величину v (рис. 10), где S — площадь основания, — высота цилиндра и n — нормаль к его основанию, Итак, при постоянной скорости v поток жидкости через плоскую поверхность Е равен Если скорость v изменяется непрерывно, а поверхность Е — гладкая, то можно разбить поверхность Е на столь малые части , чтобы каждую часть Е* можно было приближенно считать плоской и вектор v на ней постоянным.
Так как поток жидкости через поверхность Е равен сумме потоков жидкости через все ее части Е*, то мы получаем для вычисления потока приближенную формулу Векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток вектора через поверхность и его свойства Свойства потока вектора через поверхность Понятие ориентации поверхности где п — общее число частей Efc, на которые разбита поверхность Е, Рк — точка, лежащая на fc-ой части, Аак — площадь части Е* поверхности, означает скалярное произведение векторов в точке *(рис. 11).
Назовем потоком жидкости через поверхность Е предел суммы (2) при стремлении к нулю наибольшего из . диаметров площадок Е*, где d — наибольший из диаметров частей . Интеграл (3), определяющий поток жидкости, берется от скалярной функции (v, п°) по площади поверхности Е. Понятие потока произвольного вектора а через поверхность Е вводится по аналогии с введенным выше понятием потока жидкости через поверхность. Определение.
Потоком вектора {векторного поля) а через поверхность Е называется интеграл по поверхности Е от проекции вектора а на нормаль к поверхности ( = n da). Ясно, что интеграл (4) существует, если вектор непрерывен,т. е. непрерывны его координаты ), и поверхность Е — гладкая, т. е. имеетнепрерывно меняющуюся касательную плоскость. Пример 1. Поле создается точечным зарядом (электрическое поле) или точечной маосой (поле тяготения), помещенными в начале координат.
Тогда вектор напряженности поля в любой точке Р будет равен где ч — величина заряда (массы), г ОР — радиус-вектор точки Р. Требуется найти поток вектора напряженности Е через Sn — сферу радиуса R с центром в начале координат. Так как направление нормали к сфере совпадает с направлением радиус-вектора г, и поэтому На сфере 5д радиуса R имеем . Поэтому поток вектора чероз Sn равен 4.1. Свойства потока вектора через поверхность 1. Линейность. где А и ц — постоянные числа. 2. Аддитивность. Если поверхность Е разбита кусочно-гладкой кривой на две части , то поток через поверхность Е равен сумме потоков через поверхности Ei и Е2, Это свойство позволяет распространить понятие потока на кусочно-гладкие поверхности Е.
Понятие ориентации поверхности Взяв, к примеру, цилиндрическую поверхность, замечаем, что если в некоторой ее точке М выбрать определенный (один из двух) единичный вектор нормали и непрерывно перемещаться затем по поверхности вместе с соответствующим вектором нормали по любому пути, не переходящему через край поверхности, то при возвращении в точку М единичный вектор нормали совпадает с исходным (рис. 12). Вместе с тем, существуют поверхности, для которых это не так.
Примером такой поверхности может служить лист Мёбиуса (рис. 13). Существует путь (отмеченная на рисунке пунктиром средняя линия листа), перемещаясь по которому, мы возвратимся в начальную точку с единичным вектором нормали, противоположным исходному. Описанное свойство разбивает все поверхности на два класса — двусторонние, или ориентируемые (плоскость, сфера, поверхность куба и т. п.), и односторонние, или неориентируемые (лист Мёбиуса). 3. Зависимость потока от ориентации поверхности (от ориентации вектора нормали к поверхности). Понятие потока вводится только для двусторонних поверхностей.
Будем считать, что если в одной точке такой поверхности направление вектора нормали уже выбрано, то Рис. 13 в любой другой ее точке берется тот вектор нормали, который получается из выбранного при непрерывном перемещении точки по поверхности (без перехода через границу). В частности, на замкнутой поверхности во всех точках берется либо внешняя нормаль, либо внутренняя (внутренняя нормаль направлена внутрьтела, ограниченного замкнутой поверхностью).
Обозначим через ту сторону поверхности £, на которой выбран вектор нормали п+ = п, а через Е~ — сторону поверхности Е, на которой берется вектор нормали (п_ = -п). Тогда получим (7) где . Таким образом, при изменении ориентации поверхности (при изменении направления вектора нормали п° к поверхности Е) поток вектора меняет знак на противоположный.
Пример 2. Вычислить поток радиус-вектора через поверхность прямого кругового цилиндра высоты Н с радиусом основания R и осью Ог. Поверхность состоит из трех частей: боковой поверхности £j, верхнего основания £2 и нижнего основания £3 цилиндра. Искомый поток П в силу свойства аддитивности равен — потоки данного поля через и соответственно. На боковой поверхности цилиндра вектор внешней нормали п? параллелен плоскости хОу, и поэтому (см. рис. 14).
Следовательно, Векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток вектора через поверхность и его свойства Свойства потока вектора через поверхность Понятие ориентации поверхности На верхнем основании £2 вектор нормали параллелен оси Oz, и поэтому можно положить п§ = к-Тогда имеем так что На нижнем основании вектор г перпендикулярен к вектору нормали п» = -к. Поэтому Здесь символ означает двойной интеграл по замкнутой поверхности,
Если
в каждой точке
пространственной
области
задан определенный вектор
то говорят, что в этой области задановекторное
поле. Векторное
поле задается тремя скалярными функциями
,
являющимися проекциями вектора
на координатные оси декартовой системы:
.
Примерами
векторных полей могут служить поле
электрической напряженности, силовое
поле, поле скоростей текущей жидкости
и др. Векторное поле тоже может быть
плоским, например,
.
Векторной
линией поля
называется такая линия, касательная в
каждой точке которой направлена вдоль
заданного в этой точке вектора поля
(рисунок 1).
Рисунок
1
Всякое
векторное поле
обладает семейством векторных линий.
Уравнения этого семейства есть общее
решение дифференциальных уравнений
вида
.
(4)
Задача
2. Для плоского
поля
найти уравнения семейства векторных
линий и векторной линии, проходящей
через точку
Решение.
Так как
то,
согласно равенству (4), уравнение семейства
одно и определяется общим решением
дифференциального уравнения
.
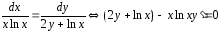
Это
уравнение линейное относительно
как функции от
.
Решая его методом вариации произвольной
постоянной, получим общее решение в
виде
.
Выделим
из этого семейства одно решение то,
которое представляет собой уравнение
векторной линии, проходящей через точку
.
Подставив в общее решение
получим
Итак, искомая векторная линия
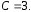
3 Поток векторного поля
Пусть
в поле вектора
задана ориентированная поверхность
.
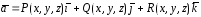
Обозначим через
единичный вектор нормали к выбранной
стороне поверхности в ее произвольной
точке. Поверхностный интеграл первого
рода по поверхности
от скалярного произведения вектора
на вектор
(5)
называется
потоком
векторного поля
через ориентированную поверхность
и обозначается
.
В случае замкнутой поверхности
поток записывается в виде
.
Если
ввести в рассмотрение вектор
и обозначить его проекции на оси координат
то формулу (5) можно переписать в виде
(6)
где
вектор
направлен по нормали к выбранной стороне
поверхности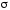
.
Правая часть равенства (6) является
поверхностным интегралом второго рода.
Если,
например,
– поле скоростей текущей жидкости в
области
и
– незамкнутая поверхность с выбранным
направлением нормали
,
то
равен количеству жидкости, проходящей
в единицу времени через поверхность
в направлении
.
Если
– замкнутая поверхность, ограничивающая
некоторую область
с внешней нормалью
,
то
равен разности количеств втекающей в
эту область жидкости и вытекающей. Когда
это означает, что в области
имеютсяисточники
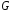
(где векторные
линии порождаются), а если
то это указывает на наличие в области
стоков
(где векторные линии заканчиваются).
Если
ориентированная поверхность
задана явно непрерывно дифференцируемой
функцией
то по формуле (6) можно получить следующую
формулу, связывающую поверхностный
интеграл по поверхности
с двойным интегралом по проекции
этой поверхности на плоскость
:
(7)
где
знак плюс берется, когда интегрирование
в левой части ведется по стороне
положительно ориентированной по
отношению к оси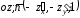
— вектор нормали к ориентированной
поверхности. Запись
означает, что в произведении
переменную
следует заменить на
Если
поверхность
задана явно уравнением
или
то соответственно меняются роли
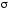
переменных в формуле (7).
Замечание.
Если
поверхность
задана уравнением
которое неоднозначно разрешается
относительно одной из переменных и,
следовательно, поверхность
неоднозначно проецируется на
соответствующую координатную плоскость
(например
— цилиндрическая поверхность неоднозначно
проецирующаяся на плоскость
),
ее следует разбить на части, однозначно
проецирующиеся на координатную плоскость.
Задача
3. Вычислить
поток вектора
через нижнюю сторону поверхности
,
отсеченной плоскостью
(рисунок 2).
Рисунок
2
Решение.
Учитывая, что
имеет различный знак
для правой и левой части поверхности
,
а
– сохраняет отрицательный знак для
всей поверхности, будем иметь
где
–
правая часть поверхности (нормаль к ней
составляет с
острый угол),
–
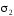
левая часть поверхности. Первые два
слагаемых уничтожаются, так как
и
имеют одинаковую проекцию на
Окончательно имеем :
где
–
проекция
на
имеет форму круга с границей
.
Поэтому, переходя к полярным координатам,
получим
Определение. Векторной линией поля 
называется векторная функция 
точки М вместе с областью её определения [5].
Задание векторного поля равносильно заданию трёх скалярных функций 
, 
, 
, являющихся проекциями на координатные оси:
.
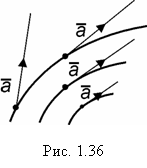
Определение. Векторной линией поля 
называется такая линия L, в каждой точке которой касательная совпадает с направлением вектора 
(рис. 1.36).
Векторная линия обычно называется линией тока при ламинарном течении жидкости (газа) и др. для поля скоростей, силовой линией – для силового поля и др.
Совокупность всех векторных линий, проходящих через точки куска поверхности вращения S, называются векторной трубкой.
Из определения векторной линии следует, что вектор 
параллельный 
. Из условия коллинеарности векторов и 
следует:
(1.95)
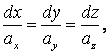
где ax, ay, az – заданные функции от x, y, z; и (1.95) является системой дифференциальных уравнений векторных линий.
Таким образом, задача нахождения векторных линий поля равносильна задаче нахождения интегральных кривых системы (1.95).
Пример 1
Найти векторные линии поля 
.
Решение. Составим систему (1.95):
Интегрируем систему. Получим:
семейство параболических цилиндров
;
семейство параболических цилиндров
.
Семейством векторных линий являются линии пересечения названных цилиндров.
Пример 2
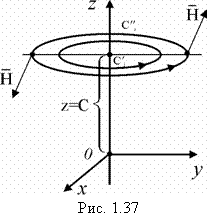
Найти векторные линии магнитного поля (вектор напряженности магнитного поля), образованного постоянным электрическим током I, текущим по бесконечно длинному проводу, совпадающему с осью Оz (рис.
1.37).
Решение. Как известно вектор напряженности магнитного поля равен:
.
Проекции 
на оси: 
Дифференциальное уравнение векторных линий имеет вид:
.
Последнее отношение имеет смысл когда z = c – постоянная величина. Оставшееся уравнение запишем так: 
Интегрируя, получим:
.
Следовательно, векторные линии поля 
определяются уравнениями: , z = c. Они являются окружностями с центрами на оси Оz, лежащие в плоскостях, перпендикулярных к этой оси (т.е. линии пересечения цилиндров и плоскостей) (рис. 1.37).
Пример 3
Вектор 
линейных скоростей частиц жидкости, вращающейся вокруг оси Оz с постоянной угловой скоростью 
, может быть представлен в виде 
, где 
– вектор угловой скорости, направленной по оси Оz; 
. точки M(x, y, z).
Найти векторные линии поля.
Решение. Найдем сначала вектор 
.Он будет найден как векторное произведение векторов и 
:
Видно, что задачу свели к предыдущей (вектор 
).
Рекомендуется в качестве упражнения проделать шаги до конца.