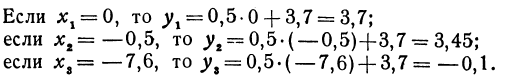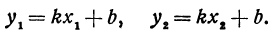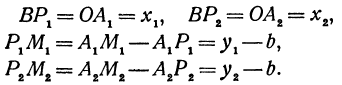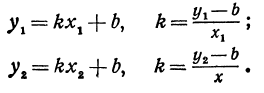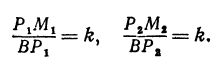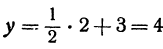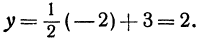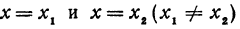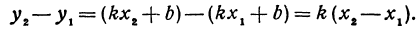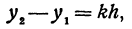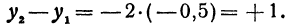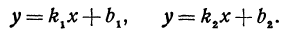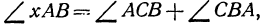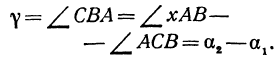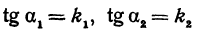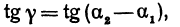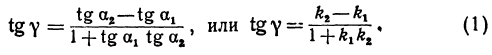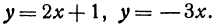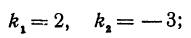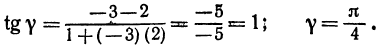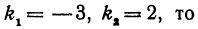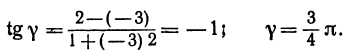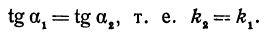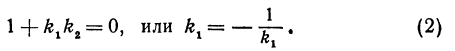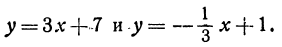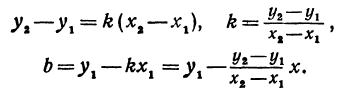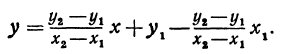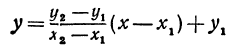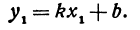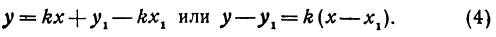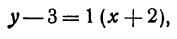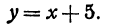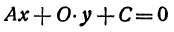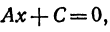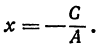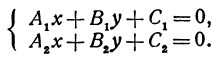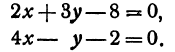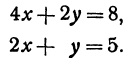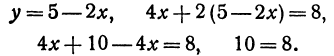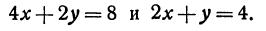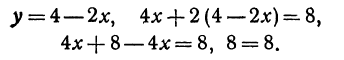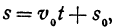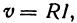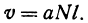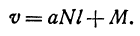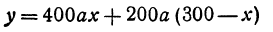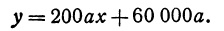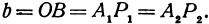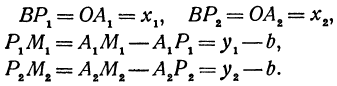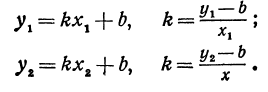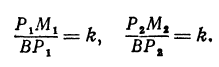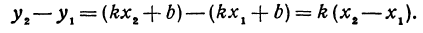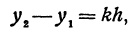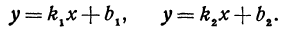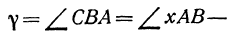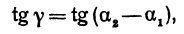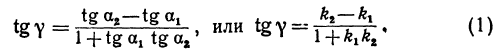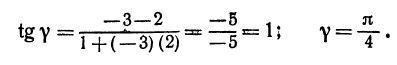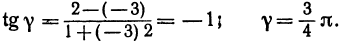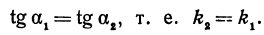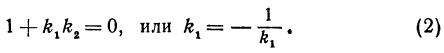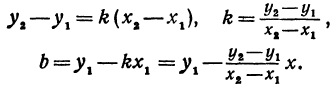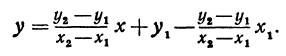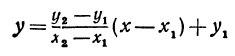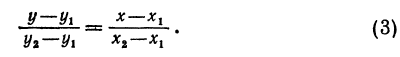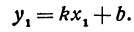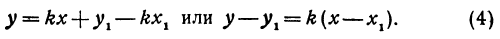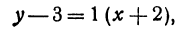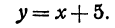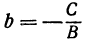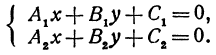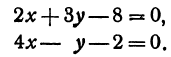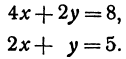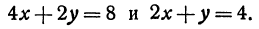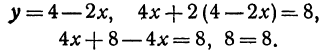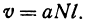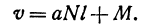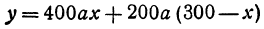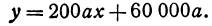Инфоурок
›
Алгебра
›Конспекты›Алгоритм определения формулы линейной функции по графику
Алгоритм определения формулы линейной функции по графику
Скачать материал
Скачать материал


- Сейчас обучается 176 человек из 51 региона




- Сейчас обучается 21 человек из 16 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 263 482 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
Тема
16. Линейная функция и её график
Больше материалов по этой теме
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Скачать материал
-
30.09.2020
54812
-
DOCX
549.2 кбайт -
253
скачивания -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 103851
-
Всего материалов:
37
Линейные функции
Движение с постоянной скоростью (или равномерное движение) по определению – это движение, при котором с изменением времени на одну и ту же величину, пройденный путь также изменяется одинаково (Рис. 1).
Рис. 1. График изменения пути при равномерном движении
Такие функции, как , у которых одинаковые изменения аргумента приводят к одинаковым изменениям значения функции (Рис. 2), называются линейными функциями.
Рис. 2. Одинаковые изменения аргумента приводят к одинаковым изменениям значениям функции
Правильнее было бы называть их прямолинейными (потому что их графиками являются прямые, о чём мы поговорим чуть позже), но прижилось именно такое сокращенное название.
Примеры линейных функций в жизни
Линейную функцию (или линейную зависимость) мы часто используем в жизни. Например, если из книги, в которой 50 страниц, мы за день прочитали 10 страниц, то можно сделать предположение, что всю книгу мы прочитаем за 5 дней (Рис. 3).
Рис. 3. Пример линейной зависимости в жизни
Или если мы идем в школу и прошли третью часть пути за 5 минут, то предполагаем, что на оставшийся путь потратим 10 минут.
Конечно, вряд ли мы будем успевать читать каждый день одно и то же количество страниц или будем идти в школу, не меняя свою среднюю скорость движения. Но для оценки значения некоторых величин, как видим, линейная функция является удобным инструментом.
Различные классы функций
Чтобы изучать какие-то объекты, их часто разбивают на группы, которые чем-то похожи. Например, разных живых организмов очень много, поэтому, чтобы их изучать, их делят на царства (животные, растения и т.д.), которые в свою очередь также делятся на более мелкие группы.
Различных функций очень много, поэтому для изучения их разбивают на разные классы. Как в жизни, мы объединяем объекты в одну группу по некоторым общим признакам (например, в супермаркете – хлебобулочные изделия, бакалея, соки-воды и т.д.), так и классы функций объединяют функции одного вида.
Линейные функции – один из этих классов (Рис. 4). Все остальные функции – нелинейные и их гораздо больше: реальные процессы описываются, в основном нелинейными функциями (Рис. 5).
Рис. 4. Линейные функции
Рис. 5. Нелинейные функции
Но, во-первых, линейные функции мы умеем изучать и описывать, а во-вторых, многие нелинейные функции в малых областях можно рассматривать как линейные (Рис. 6).
Рис. 6. Приближение нелинейных функций линейными
Значит, линейные функции можно использовать как удобный инструмент для изучения других функций.
Конечно, линейные функции – не единственный класс функций, который мы умеем и будем изучать. Ещё будут квадратичные функции, показательные, обратная пропорциональность и т.д. Но о них поговорим позже.
Аналитическое задание линейной функции и ее характеристическое свойство
Итак, линейные функции часто встречаются и их можно изучать. Поэтому на этом уроке мы и займемся этим классом функций.
Аналитически линейная функция задается формулой , где
и
– произвольные заданные числа,
– угловой коэффициент,
– свободный коэффициент (свободен от
).
Ее характеристическое свойство (т.е. свойство, которым обладают только линейные функции, ее эквивалентное определение) состоит в том, что при изменении аргумента на одну и ту же величину значение функции так же изменяется на одну и ту же величину.
Только для линейных функций совершенно неважно, изменился на
от
до
или от
до
и т.д. –
тоже изменится одинаково (Рис. 7).
Рис. 7. Эквивалентное определение линейной функции
Например, растём мы нелинейно (с до
лет и с
до
изменение роста сильно отличается), бегаем – тоже (бежать первый километр значительно легче, чем, например, пятый) и т.д.
Линейное уравнение с двумя переменными
Рассмотрим линейное уравнение .
Мы уже умеем его решать – для этого перенесем число из левой части в правую, затем разделим на коэффициент при переменной:
Рассмотрим похожее уравнение . Его решение будет практически таким же:
Аналогично:
Обобщим рассмотренные уравнения и напишем в правой части число , решение от этого не изменится:
Когда меняется значение , меняется и значение
. Если мы не знаем значение
, то тогда в уравнении
две неизвестных:
и
.
Уравнение вида называют линейным уравнением с двумя переменными, где
– переменные,
– произвольные числа.
Перепишем уравнение следующим образом:
.
Если , то на него мы можем разделить обе части уравнения:
.
Перепишем так, чтобы один член был с переменной , а второй – без:
Переобозначим коэффициенты:
Тогда .
Т.е. линейное уравнение с двумя переменными задает линейную функцию.
Рассмотрим отдельно случай, когда :
При мы получим
. Или просто
.
Такое уравнение тоже задает прямую (только вертикальную), но линейной функцией не является, т.к. одному значению
(
) соответствует бесконечное множество значений
(Рис. 1).
Рис. 1. Одному значению соответствует бесконечное множество значений
Построение графика линейной функции
Чтобы охарактеризовать поведение функции, обычно строят ее график.
Пример 1. Построить график функции .
Решение:
Найдем несколько значений при различных значениях
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь возьмем пары и отметим их в декартовой системе координат (Рис. 8).
Рис. 8. Построение графика линейной функции
Соединим отмеченные точки линией (Рис. 9).
Рис. 9. Построение графика линейной функции
Похоже, что все точки лежат на одной прямой. И на самом деле графиком любой линейной функции является прямая.
Полученная прямая и есть график линейной функции .
На уроках геометрии мы уже обсуждали, что через две точки можно провести только однупрямую. Поэтому, если мы найдем две точки, которые принадлежат графику линейной функции (т.е. прямой), мы сможем его построить. Вывод: для построения графика линейной функции достаточно найти координаты двух точек, которые ей принадлежат (найти значения
при любых двух значениях
).
Интерполяция и аппроксимация
При проведении различных исследований возникает такая задача: по некоторым известным значениям функции попытаться восстановить саму функцию (график или формулу) (Рис. 1). Если мы знаем, что функция линейная, то достаточно двух значений (прямая однозначно задаётся двумя точками).
Рис. 1. Восстановление функции по некоторым известным значениям функции
Например, сила растяжения пружины зависит от растяжения пружины по закону Гука (Рис. 2).
Достаточно измерить силу для двух различных значений растяжения пружины, чтобы найти жёсткость пружины (коэффициент ) и восстановить функцию (Рис. 3).
Рис. 2. Закон Гука
Рис. 3. Нахождение жёсткости пружины при помощи закона Гука
Но можно ли попытаться восстановить функцию, не зная, какой вид она имеет? (Рис. 4).
Рис. 4. Восстановление функции, вид которой заранее неизвестен
Такая задача называется аппроксимацией – на основании экспериментального набора значений функции в нескольких точках построить функцию, на которую с высокой точностью попадут получаемые в ходе эксперимента значения (как те, что у нас уже есть, так и остальные, которые можно получить).
Если мы хотим, чтобы построенной функции точно принадлежали все имеющиеся значения функции, то этот частный случай аппроксимации называется интерполяцией.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации (т.е. приближении) какой-либо сложной функции другой, более простой функцией. (Рис. 5).
Рис. 5. Приближение сложной функции к более простой
Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но для некоторых задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Подробнее почитать об интерполяции и аппроксимации можно в Интернете.
Пример 2. Построить график функции .
Решение:
Возьмем два произвольных значения переменной , например, 0 и 4.
Двух точек нам достаточно, чтобы построить прямую. Поэтому возьмем полученные пары , отметим их в декартовой системе координат и соединим их линией (Рис. 10).
Рис. 10. Иллюстрация к примеру 2
Частные случаи линейных функций
Отдельно рассматривают два частных случая линейной функции :
,
.
Если , то функцию
называют прямой пропорциональностью. Ее график всегда проходит через начало координат. Например,
(Рис. 11).
Рис. 11. Графики прямой пропорциональности
О втором типе линейных функций мы поговорим чуть позже.
Угловой коэффициент 
Название углового коэффициента неслучайно: в зависимости от его значений будет изменяться угол наклона прямой по отношению к положительному направлению оси абсцисс.
1. – угол наклона острый.
Рассмотрим на примере функции (Рис. 12).
Рис. 12. Угловой коэффициент
2. – угол наклона тупой.
Рассмотрим на примере функции (Рис. 13).
Рис. 13. Угловой коэффициент
3. – прямая параллельная оси абсцисс.
Рассмотрим на примере функции (Рис. 14).
Рис. 14. Угловой коэффициент
Теперь посмотрим, какое значение будет принимать функция , когда
:
Мы получили, что графику прямой принадлежит точка , это его точка пересечения с осью ординат (Рис. 15).
Рис. 15. Значение линейной функции при
Параллельность и пересечение прямых
Мы знаем, что на плоскости две прямые могут или пересекаться, или быть параллельными. Зададим условия, при которых графики двух линейных функций будут параллельны.
Прямые и
будут параллельными тогда, когда у них совпадают угловые коэффициенты:
. Например,
;
;
(Рис. 16).
Рис. 16. Параллельные прямые
Доказательство
Пусть у нас есть две различных прямых, у которых равны угловые коэффициенты (Рис. 1).
Рис. 1. Прямые с одинаковыми угловыми коэффициентами
Докажем, что эти прямые параллельны, методом от противного.
Пусть они непараллельны, т.е. пересекаются, тогда существует точка с абсциссой , в которой их значение совпадает (Рис. 2).
Рис. 2. Предположение, что прямые пересекаются в точке
Перепишем в эквивалентном виде: .
Тогда , т.е. прямые совпадают. Получили противоречие, т.к. заданы разные прямые. Значит, наше предположение неверно, прямые не пересекаются, т.е. они параллельны.
Прямые и
пересекаются тогда, когда их угловые коэффициенты не равны:
. Например,
,
(Рис. 17).
Рис. 17. Пересекающиеся прямые
Перпендикулярность
Для пересекающихся прямых можно выделить особый случай, когда при пересечении получаются равные углы (прямые), т.е. прямые перпендикулярны (Рис. 1).
Рис. 1. Перпендикулярные прямые
Прямые и
перпендикулярны, когда выполнено
.
Пример 1
Графики этих функций действительно перпендикулярны (Рис. 2).
Рис. 2. Пример перпендикулярных прямых
Заключение
На этом уроке мы познакомились с линейной функцией (функцией, у которой при одинаковом изменении аргумента одинаково меняется значение самой функции).
Аналитически такие функции задаются уравнением , где
– произвольные числа,
– угловой коэффициент,
– свободный коэффициент.
Ее график – прямая. Чтобы его построить, достаточно найти две точки, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент – за точку пересечения графика функции с осью ординат.
Прямые параллельны, если их угловые коэффициенты равны () и пересекаются, если
.
Список рекомендованной литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, издательство «Просвещение», 2017.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник, издательство «Просвещение», 2014.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник, издательство «Просвещение», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал youclever.org (Источник)
- Интернет-портал tofmal.ru (Источник)
Домашнее задание
- Линейная функция задана формулой
. Найти значение
, соответствующее
. При каком значении
значение
равно
?
- Построить график функции, заданной уравнением:
.
- У ученика было
рублей. На эти деньги он купил
марок по
рублей. После покупки у него осталось
рублей. Задать формулой зависимость
от
. Является ли эта зависимость линейной?
Линейная функция — функция вида y=kx+b (для функций одной переменной).
Определение и геометрический смысл
Рассмотрим уравнение с двумя неизвестными х и у:
где 
Например, уравнению
удовлетворяют следующие пары:
и т. д.
Для того чтобы найти пару чисел, удовлетворяющих уравнению ( * ), нужно придать х произвольное числовое значение и подставить в уравнение ( * ), тогда у получит определенное числовое значение. Например, если х = 27, то у = 2 x 27 — 6 = 48. Очевидно, что пара чисел х =27 и у =48 удовлетворяет уравнению (*). Так же и в случае уравнения (1) можно придать х произвольное числовое значение и получить для у соответствующее числовое значение.
Так как в данном уравнении х может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то х называют независимой переменной величиной или аргументом.
Для у получаются также различные значения, но уже в зависимости от выбранного значения х; поэтому у называют зависимым переменным или функцией.
Функцию у, определяемую уравнением (1), называют линейной функцией.
Пример:
Вычислить значения линейной функции, определяемой уравнением у = 0,5х + 3,7, при следующих значениях независимого переменного: х1 = 0, х2 = —0,5, х3 = —7,6.
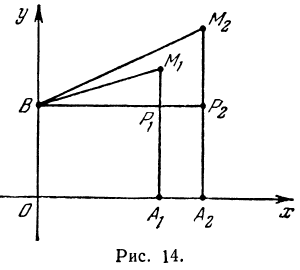
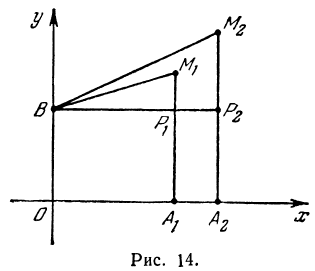
Покажем, что если принять пару чисел х и у, удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).
В самом деле, рассмотрим точку В(0, b) и точки М1(х1, у1) и М2(х2, у2), координаты которых удовлетворяют уравнению (1), т. е.
Обозначим проекции точек М1 и М2 на ось Ох через А1 и A2, тогда ОА1 = х1, ОА2 = х2, А1М1= у1, А2М2 = у2. Проведем из точки В прямую, параллельную оси Ох. При этом получим b = ОВ = А1Р1 = А2Р2.
Предположим, что точки BМ1 и М2 не лежат народной прямой. Соединяя точку В с точками М1 и М2, получим два прямоугольных треугольника ВР1М1 и ВР2М2, из которых имеем:
Но так как х1, у1 и х2, у2 удовлетворяют уравнению (1), то
Иначе говоря,
Выражения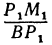
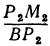








Так как М1 и М2 — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси Оу отрезок ОВ = b и образующей с положительным направлением оси Ох угол а такой, что tg a = 
Число b называется начальной ординатой, число 
Предыдущие рассуждения позволяют сделать вывод: линейная функция y = 

Например, линейная функция 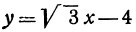
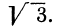
Если имеем определенную прямую, отсекающую на оси Оу отрезок b и наклоненную к оси Ох под углом 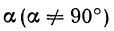
Очевидно, имеет место и такое предложение:
Всякой прямой, отсекающей на оси Оу отрезок b и наклоненной к оси Ох под углом, тангенс которого равен числу 

Координаты любой тонки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение у = 
Отметим частные случаи.
1.Пусть b = 0, т. е. линейная функция определяется уравнением
Прямая, определяемая этим уравнением, проходит через начало координат. Здесь у пропорционален х, т. е. если х увеличить (уменьшить) в несколько раз, то и у увеличится (уменьшится) во столько же раз.
2.Пусть 
Этому уравнению соответствует прямая, параллельная оси Ох и отстоящая от нее на расстояние b.
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Задача:
Даны точки А (3, 5) и В(— 1, 4). Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид
Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки А в уравнение (*), получим 5 = 2 x 3 — 1. Это тождество, следовательно, точка А лежит на прямой. Подставляя координаты точки В, получаем 4 = 2(— 1)—1 = —3. Отсюда видно, что точка В не лежит на прямой.
Задача:
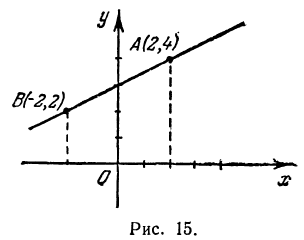
Построить прямую, уравнение которой
Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим х произвольное значение, например х = 2, и найдем из уравнения (**) значение
Значит, точка A (2, 4) лежит на прямой.
Это первая точка. Теперь дадим х какое-нибудь другое значение, например х = —2, и вычислим у из уравнения (**).
Получим
Точка B ( — 2, 2) лежит на прямой. Это вторая точка. Строим точки A и B (рис. 15) и проводим через них прямую, это и есть искомая прямая.
Основное свойство линейной функции
Рассмотрим линейную функцию у = 
Здесь первое и второе значения х различны, они отличаются друг от друга на величину х2 — х1. Величину разности х2 — х1, на которую изменяется x при переходе от x1 к х2, назовем приращением независимого переменного х. Эту величину часто будем обозначать через h, так что h = x2 — x1. Найдем, насколько изменилось значение у при изменении х1 на h . Для этого вычтем из у2 значение у1
Таким образом,
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции. Заметим, что х2 может быть больше, а может быть и меньше, чем х1. Поэтому h = x2 — x1 может быть как положительным, так и отрицательным числом, иначе говоря, приращение h независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине у2—у1.
Пример:
Найдем приращение функции y = 0,6x—3, если приращение независимого переменного h = 0,1.
По основному свойству у2—у1 = 0,6 x 0,1 = 0,06.
Приращение этой же функции y = 0,6x—3 , если h = —3, будет равно у2—у1 = 0,6 x (— 3) = —1,8. В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
Пример:
Найдем приращение функции у = —2x+10 при изменении х на h = —0,5. Будем иметь
Задачи на прямую
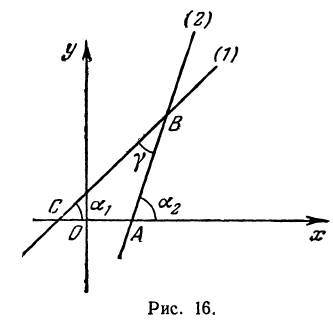
Задача:
Найти угол y между двумя прямыми, заданными уравнениями
Решение:
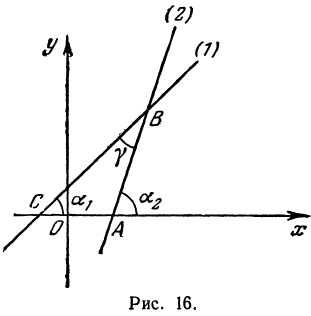
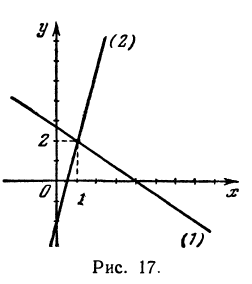
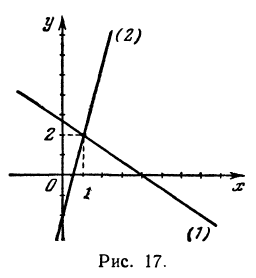
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
Угол хАВ является внешним по отношению к треугольнику ABC, поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е.
откуда
Но углы а1 и а2 непосредственно неизвестны, а известны их тангенсы
Поэтому напишем
или
Пример:
Найти угол между прямыми, заданными уравнениями
Здесь
применяя формулу (1), получим;
Если же будем считать, что
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы а1 и а2 равны, как соответственные, следовательно, тангенсы их тоже равны
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 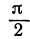
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями
Здесь угловые коэффициенты (первый равен 3, а второй 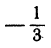
Задача:
Даны две точки: M1(x1, у1) и М2(х2, у2), где 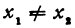
Решение:
Искомая прямая не параллельна оси Оу, поэтому ее уравнение можно написать в виде 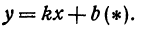

Так как прямая проходит через точки М1 и М2, то координаты этих точек должны удовлетворять уравнению ( * ), т. е.
В уравнениях ( ** ) и (*** ) все числа, кроме 

Подставляя найденные выражения в уравнение (*), получим
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси Оу.
Полученному уравнению можно придать форму, удобную для запоминания, а именно:
или
Задача:
Написать уравнение прямой, проходящей через данную точку М(х1,у1) и образующей с осью Ох угол а.
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла а. Обозначим 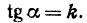
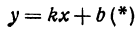
Находим отсюда неизвестное b, получим 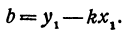
Это и есть уравнение прямой, проходящей через точку М в заданном направлении.
Если в уравнении (4) менять направление, не меняя точку M, то получим уравнение всех прямых, проходящих через заданную точку. Уравнение 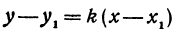

Пример:
Напишем уравнение прямой, проходящей через точку М( — 2, 3) и образующей с осью Ох угол 45°.
Так как tg 45° = 1, то угловой коэффициент равен 1; х1 = —2; у1 = 3. Уравнение прямой запишется в виде
или
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными
Решим его относительно у:
т. е. мы получили линейную функцию, где 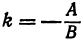
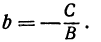
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой.
Рассмотрим особо случай, когда B = 0, так как на нуль делить нельзя.
Уравнение (1) примет вид
или
откуда
Поэтому, каков бы ни был у, х всегда равен 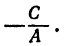
Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
Из уравнения (1) (если 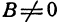
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке).
Рассмотрим систему двух уравнений
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения х и у, которые удовлетворяют и первому и второму уравнениям. Но так как х и у определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
Пример:
Найдем точку пересечения двух прямых:
Решая эту систему, получим: х = 1, у = 2, т. е. прямые пересекаются в точке (1,2) (рис. 17).
Пример:
Найдем точку пересечения двух прямых:
Решая эту систему, получим:
Последнее равенство нелепо, значит, прямые не пересекаются, Рис. 17. т. е. они параллельны.
Пример:
Найдем точку пересечения данных прямых
Решая эту систему, получим:
Полученное равенство всегда справедливо, т. е. справедливо при любом значении x. Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры решения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения
где — начальное расстояние, v0 — скорость, t — время; это, как мы уже знаем, есть линейная функция.
Пример:
Закон Ома записывается в виде
где v — напряжение, R — сопротивление и I — ток. Если не изменяется, то v является линейной функцией тока I .
Пример:
Если стоимость провоза единицы товара по железной дороге равна а руб. за километр, то стоимость v провоза N единиц товара на l км равна
Если же стоимость товара на месте равна М руб., то после перевозки за него надо заплатить
Здесь v—линейная функция l.
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Задача:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А и В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В—200 т. Перевозка одной тонны нефти на один километр обходится в а руб.
Решение:
Обозначим расстояние от А до предполагаемого пункта С через х. Тогда расстояние от города В до С равно 300 — х. Стоимость перевозки одной тонны нефти из С в A равна ах руб., а перевозки 400 т—400аx руб. Аналогично перевозка нефти из С в В будет стоить 200а (300 — х) руб. Стоимость всех перевозок, которую обозначим через у, будет выражаться так:
или
Это линейная функция. Если примем х за абсциссу, а у за ординату точки, то полученная линейная функция определяет уравнение некоторой прямой. Угловой коэффициент ее равен 200а, т. е. положителен, следовательно, эта прямая образует с осью Ох острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина х заключена между 0 и 300, т. е. 
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе A, если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к A, тем выгодней.
Примеры применения линейной функции
Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Выпуклые множества точек
- Система координат
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2×0 – 1= –1;
у=2х – 1=2×3 – 1= 5.
Вписываем в таблицу значения у:
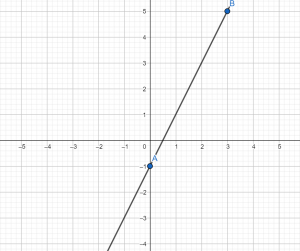
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
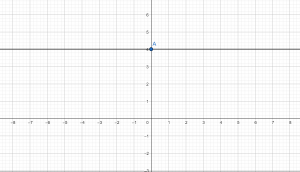
Пример №3
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
Задание OM1106o
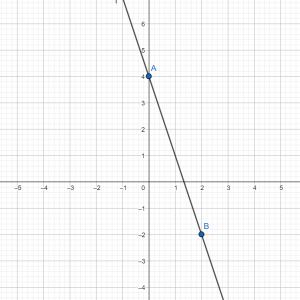
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор
Задание OM1103o
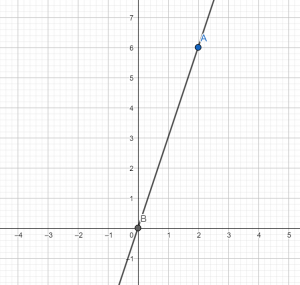
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 6.1k
Содержание:
Рассмотрим уравнение с двумя неизвестными
где 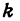
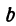
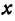
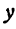
Например, уравнению
удовлетворяют следующие пары:
и т. д.
Для того чтобы найти пару чисел, удовлетворяющих уравнению 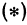

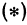

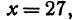
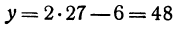
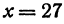
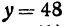
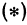


Так как в данном уравнении 

Для 


Функцию 
Пример:
Вычислить значения линейной функции, определяемой уравнением 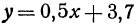
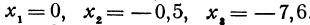
Решение:
Если 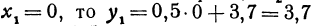
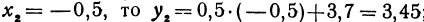
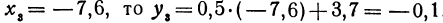
Покажем, что если принять пару чисел 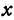
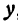
В самом деле, рассмотрим точку 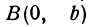
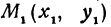
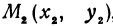
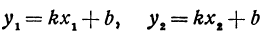
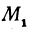
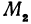
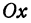
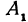
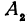
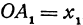

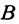
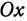
Предположим, что точки 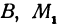
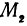
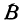
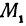
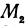
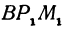
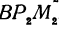
Но так как 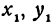
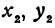
Иначе говоря,
Выражения 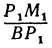
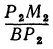
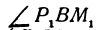
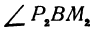
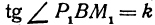
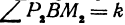

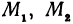
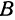
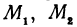
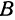
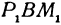
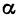
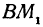
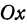
Так как 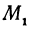
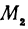
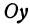
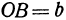
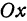
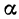
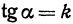
Число 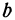
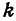
Предыдущие рассуждения позволяют сделать вывод: линейная функция 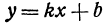
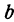
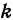
Например, линейная функция 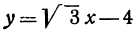
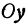
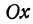
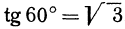
Если имеем определенную прямую, отсекающую на оси 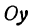
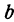
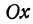
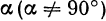
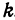
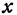
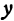
Очевидно, имеет место и такое предложение: Всякой прямой, отсекающей на оси 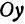
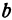
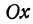
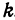
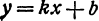
Координаты любой, точки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение 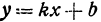
Таким образом, всякая линейная функция является уравнением некоторой прямой.
Отметим частные случаи.
1. Пусть 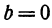
Прямая, определяемая этим уравнением, проходит через начало координат. Здесь 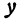
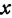
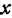
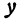
2. Пусть 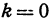
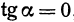
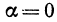
Этому уравнению соответствует прямая, параллельная оси 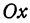
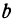
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Пример:
Даны точки 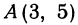
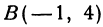
Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки 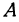
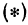
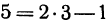
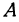
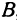
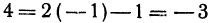
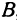
Пример:
Построить прямую, уравнение которой
Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим 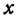
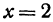
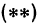
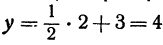
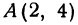
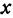
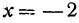
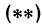
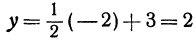
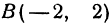
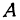
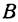
Основное свойство линейной функции
Рассмотрим линейную функцию 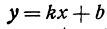
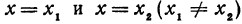
Здесь первое и второе значения 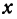
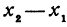

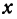
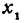
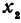
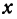
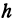
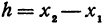
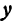
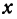
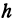
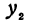
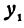
Таким образом,
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции.
Заметим, что 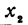
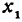
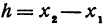
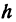
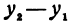
Пример:
Найдем приращение функции 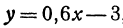
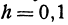
Решение:
По основному свойству 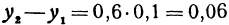
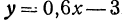
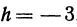
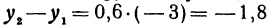
Пример:
Найдем приращение функции 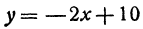
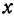

Будем иметь
Задачи на прямую
Пример:
Найти угол 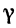
Решение:
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
Угол 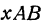
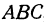
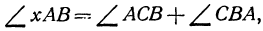
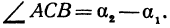
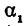
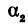
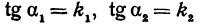
или
- Заказать решение задач по высшей математике
Пример:
Найти угол между прямыми, заданными уравнениями 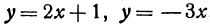
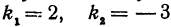
Решение:
Применяя формулу (1), получим:
Если же будем считать, что 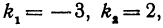
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы 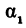
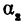
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 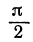
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями 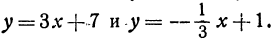
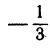
Решение:
Следовательно, рассматриваемые прямые перпендикулярны.
Пример:
Даны две точки: 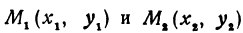
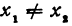
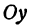
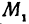
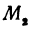
Решение:
Искомая прямая не параллельна оси 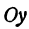
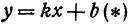
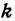
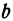
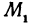
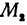
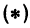
В уравнениях 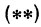
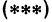
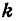
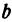
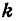
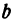
Решая систему, находим:
Подставляя найденные выражения в уравнение 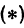
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси 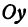
или
Пример:
Написать уравнение прямой, проходящей через данную точку 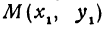
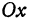
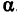
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла 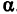
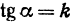
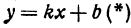
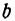
Так как прямая должна проходить через точку 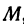
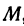
Находим отсюда неизвестное 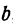
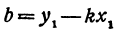
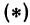
Это и есть уравнение прямой, проходящей через точку 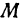
Если в уравнении (4) менять направление, не меняя точку 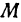
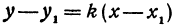
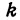
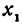
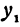
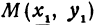
Пример:
Напишем уравнение прямой, проходящей через точку 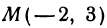
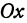
Решение:
Так как 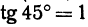
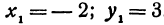
или
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными
Решим его относительно 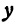
т. е. мы получили линейную функцию, где 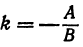
Уравнения (1) и (2) равносильны, поэтому пара чисел 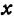
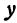
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой. Рассмотрим особо случай, когда 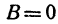
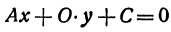
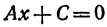
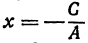
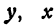
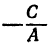
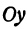
Из уравнения (1) (если 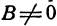
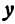
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке). Рассмотрим систему двух уравнений
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения 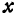
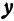
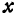
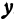
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: 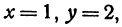
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: 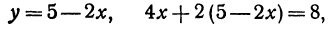
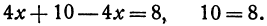
Пример:
Найдем точку пересечения данных прямых
Решение:
Решая эту систему, получим:
Полученное равенство всегда справедливо, т. е. справедливо при любом значении 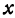
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры применения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения 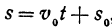
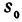
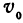
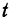
Пример:
Закон Ома записывается в виде 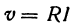
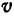
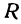
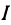
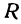
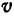
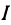
Пример:
Если стоимость провоза единицы товара по железной дороге равна 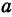
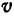
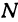
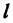
Если же стоимость товара на месте равна 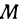
Здесь 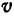
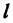
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Пример:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А к В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В —200 т. Перевозка одной тонны нефти на один километр обходится в 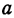
Решение:
Обозначим расстояние от А до предполагаемого пункта С через 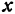
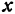
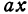
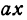
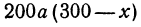
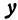
или
Это линейная функция. Если примем 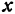
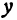
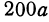
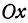
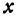
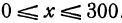
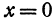
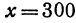
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе А; если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к А, тем выгодней.
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Производная сложной функции
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Координаты на плоскости