Как найти уровень шума в сигнале

В данном посте освещены 3 темы по основам цифровой обработки сигналов:

• Виды шумов, отношение сигнал/шум,
• Статистическая обработка сигнала,
• Корреляционная функция.

Виды шумов, отношение сигнал/шум.

В данной публикации мы поговорим о характеристиках случайных процессов, познакомимся с разными видами шумов, и узнаем о важном определении – отношение сигнал/шум. Начнём с характеристик.

Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием.

Насколько сильно значения случайного процесса могут отличаться от матожидания описывает параметр дисперсия, мера разброса случайной величины.

Также в качестве меры разброса употребляется среднеквадратичное отклонение, также именуемое стандартным отклонением. Значение его — квадратный корень из дисперсии.

На рисунке представлены нормальные распределения 4-х случайных процессов с разными значениями матожидания и дисперсии. В случае большего значения дисперсии колокол гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений, и меньшей вероятности значений, близких к матожиданию.

В качестве меры скорости изменения случайного процесса может использоваться авто-корреляционная функция или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.

В случае нулевого сдвига сигналы полностью совпадают, и значение авто-корреляционной функции максимально. При увеличении расхождения это значение уменьшается, причём для слабо изменяющихся во времени сигналов спад функции происходит медленнее, чем для быстро изменяющихся.

Математическое ожидание, дисперсия, авто-корреляционная функция – это примеры численных характеристик, которыми можно описать случайный процесс.

Законы изменения реальных физических величин весьма сложны, и для того, чтобы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определённые допущения. При описании сигналов случайными процессами мы часто оговариваем свойства стационарности и эргодичности.

Стационарым процесс называется в том случае, когда его плотность вероятности не зависит от временного сечения. То есть его статистические характеристики – матожидание, дисперсия, коореляционная функция – не будут зависеть от времени.

Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализаций мы можем использовать усреднение по времени одной реализации. На практике нам обычна доступна только одна реализация случайного процесса.

Ещё одна важная характеристика случайного процесса – спектральная плотность мощности. По определению, это распределение мощности сигнала в зависимости от частоты, то есть мощность, приходящаяся на единичный интервал частоты.

Мы можем рассматривать спектральную плотность мощности как ещё одну меру скорости изменения случайного процесса. Она связана с корреляционной функцией случайного процесса теоремой Винера-Хинчина-Колмогорова, и с ней я советую познакомиться самостоятельно.

А мы пока что рассмотрим два синусоидальных сигнала разной частоты. В частотной области эти сигналы будут представлены двумя линиями. Положение линии на оси Х говорит о величине частоты синусоиды, а длина линии – о её мощности или амплитуде.

Случайные процессы мы также можем рассматривать как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющихся быстро или медленно. Спектр медленно изменяющегося случайного процесса содержит больше синусоид, или спектральных компонент, в левой части оси f – то есть в зоне низких частот. В то время как спектр быстро меняющегося процесса содержит больше компонент большей амплитуды в левой части частотной оси.

Слуйчайный процесс, у которого область частот заполнена равномерно, называется белым шумом.

Белый шум – это стационарный слуйчайный процесс с равномерно распределённой спектральной плотностью мощности. В таком процессе присутствуют компоненты, изменяющиеся быстро, медленно, средне, и ни одна из них не преобладает над другими.

Белый шум получил свой название по аналогии со спектром белого света. Нам известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона. Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определённым цветом можно обозначить преобладание в спектре сигнала определённых компонент. Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты. Если наложим синий фильтр – получим сигнал с относительно высокими частотами в спектре.

Цветовое обозначение частотного состава используется для описания так называемых цветных шумов. Они никак не привязаны к какому-либо конкретному частотному диапазону, и различаются только видом их спектральной плотностью мощности. Сразу оговорюсь, что цветные шумы, в том числе и белый шум – это модели шумов, приближающие некоторые физические явления. К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к так называемому фликкер-шуму, который достаточно успешно описывается моделью розового шума. Красный шум описывает броуновское движение, модель серого шума используется в психоакустике и так далее.

Какая же модель шума чаще всего используется в цифровой обработке сигналов? Это аддитивный белый гауссовский шум.

• У него равномерная спектральная плотность мощности, поэтому он белый.
• Нормальное распределение, поэтому он Гауссовский.
• С полезным сигналом он суммируется, поэтому он аддитивный.
• И  статистически он от сигнала независим.

На системы беспроводной связи и обработки сигналов воздействуют множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме распределение их суммарного воздействия будет близко к нормальному.

Именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных. Шум в подобных системах, конечно же, является нежелательным явлением.

Одной из мер качества системы является отношение сигнал/шум. Это безразмерная величина, равная отношению мощности полезного сигнала к мощности шума. Отношение сигнал/шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться. Но в любом случае, чес выше этот показатель, тем лучше.

Одна из задач цифровой обработки сигналов – повышение отношения сигнал/шум. Существуют разные способы повышения. О фильтрации мы поговорим в дальнейших публикациях, а сейчас давайте познакомимся с усреднением, или когерентным накоплением.

Если мы сложим два одинаковых сигнала в фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные – с отрицательными. Но сложить две реализации случайного процесса в фазе не получится. В каких-то точках произойдёт усиление, в каких-то – ослабление шума. Проще говоря, при усреднении амплитуда шума не растёт.

Давайте рассмотрим пример накопления сигнала с шумом в MATLAB.

Мы генерируем синусоиду, и добавляем к ней аддитивный белый Гауссовский шум при помощи функции awgn. Функция эта содержится в расширении MATLAB Communications Toolbox. На её вход мы подаём исходный незашумлённый сигнал, и параметр отношения сигнал/шум в децибелах. Строим на графике сигнал с шумом и без шума.

Затем мы выделим только шумовую компоненту, вычитаем из смеcи сигнал/шум исходный сигнал. Визуализируем его отсчёты командой stem. Функция периодограм позволит нам оценить спектральную плотность мощности нашего шума. Мы видим, то что распределение действительно равномерное, это белый шум.

Гистрограмма показывает нам, что распределение значений вектора noise близко к нормальному. 

Теперь мы генерируем большое число зашумлённых сигналов.  Несмотря на то, что мы вызываем одну и ту же команду, реализации шума в каждом из векторов будут отличаться. Можем убедиться в этом, отразив четыре первых вектора на графике.

Если мы будем складывать эти вектора между собой, то их синусоидальная компонента будет всегда складываться в фазе, в то время как шумовые компоненты будут складываться случайным образом. Убедимся в том, что амплитуда шума в результирующей сумме заметно ниже.

В завершении давайте поговорим о ещё двух хар-ках системы, которые непосредственно связаны с шумом.

Динамический диапазон – это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу – так называемым шумовым дном, или чувствительностью.

Чувствительность – это численный параметр, равный уровню сигнала, различимого системой над шумами. Если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счёт этого способна различать сигналы малой энергетики.

В следующей публикации мы подробнее поговорим о статистических параметрах сигнала.

Наверх

Статистическая обработка сигнала.

В этой публикации мы под робнее поговорим о статистической обработке сигналов. Давайте вспомним, какие статистические параметры мы рассматривали, когда говорили о случайных процессах. Когда мы рассматривали случайный процесс с нормальным распределением мы оперировали понятиями математического ожидания  и дисперсии. Когда мы рассматриваем сигналы в общем виде, то у них так же есть статистические показатели со схожим смыслом.

У любого сигнала, непрерывного и дискретного, можно определить среднее значение. Оно может вычисляться по-разному.

Если мы ищем среднее арифметическое, то для этого мы складываем все отсчёты сигнала и делим сумму на количество отсчётов.

Но также в качестве среднего значения для дискретной последовательности может применяться медианное значение. При его вычислении все элементы дискретного сигнала выстраиваются по возрастанию, и находится центральный элемент упорядоченной последовательности.

То, что мы называли дисперсией случайного процесса, у произвольного сигнала может именоваться отклонением от среднего значения. Для колебательных процессов отклонение по сути – это амплитуда колебаний.

Для любого сигнала мы можем определить минимальное и максимальное значение на отрезке наблюдения. Минимум и максимум сигнала определяют его размах, или динамический диапазон.

Ну и скорость изменения сигнала может характеризоваться корреляционной функцией. Её мы подробно рассмотрим в следующей публикации.

Статистические показатели реальных сигналов часто изменяются во времени. К примеру, при относительной стабильности амплитуды колебаний во времени, среднее значение, вокруг которого изменяется сигнал, может «плавать».

При обработке зачастую выбирают некоторые временные рамки относительной стабильности статистических характеристик, и подсчитывают эти характеристики для коротких отрезков исходного сигнала. Временной интервал, на котором рассматривается сигнал, называется окном. И окно это обычно перемещается или скользит по исходному сигналу.

Подобным образом мы можем находить локальные статистические характеристики, такие как, например, локальные средние значения, или локальные минимумы и максимумы. Подобная обработка позволяет отслеживать постоянную составляющую сигнала, которую мы также называем трендом, и находить пики или спады на графике сигнала.

Рассмотрим пример нахождения тренда или меняющейся во времени постоянной составляющей сигнала методом скользящего среднего. Как вы поняли из названия, этот метод подразумевает нахождение локального среднего арифметического. Окно перемещается по сигналу, и в результате обработки формируется выходной вектор, в отсчёты которого записываются значения среднего арифметического для каждого шага.

Результирующий вектор становится сглаженным, по сравнению с исходным. И чем больше размер окна – тем больше степень сглаживания. Можно использовать небольшие окна для сглаживания формы сигнала и избавления от нежелательных высокочастотных колебаний, либо можно взять большое окно для выделения постоянной составляющей.

Если рассматривать процесс вычисления среднего значения, как набор арифметических операций над каждым из отсчётов, попавших в окно, то в случае со скользящим средним каждый отсчёт умножается на величину, обратную размеру окна, и затем все результаты произведения складываются.

Если мы берём окно не из трёх, а из пяти элементов, то и коэффициент становится равным одной пятой. Но коэффициенты не обязательно должны быть одинаковыми. В общем случае мы рассматриваем операцию нахождения взвешенного среднего. Окна с разнообразными коэффициентами могут усиливать или ослаблять различные частотные компоненты сигнала. Процесс взвешенного усреднения – одна из форм цифровой фильтрации. О цифровых фильтрах мы будем подробно говорить в других публикациях. А пока что давайте осуществим статистическую обработку сигнала в MATLAB.

 

Мы вновь проанализируем сигнал ЭКГ, но в этот раз мы попробуем выделить из него так называемый Q-R-S комплекс, то есть определить положение Q-, R-, S-зубцов в наших данных. Но наши данные зашумлены и постоянная составляющая у сигнала изменяется во времени, что может помешать нам выделить искомое зубцы. Поэтому нам необходимо отфильтровать наши данные, избавиться от постоянной составляющей и выделить локальные экстремумы. Для фильтрации и удаления тренда мы можем воспользоваться одной и той же функцией movmean из состава Signal Processing Toolbox. Она у нас выполняет операцию скользящего среднего. Если мы возьмём маленькое кошка из 10 отсчётов, то мы сгладим форму нашего сигнала. А если мы возьмём большое окно из 300 отсчётов, то мы выделим постоянную составляющую. Отразим её на том же графике.

Для выделения пиков наших Q-, R-, S-зубцов воспользуемся встроенной функцией findpeaks. Выделение R-, S-зубцов происходит достаточно просто, мы просто берём выбросы величины, которые больше чем 0,5 или меньше чем –0,5 и отображаем их на том же графике.

А вот для выделения Q-зубцов нам придется воспользоваться логической индексацией. Мы знаем то, что Q-выброс лежит в пределах от –0,2 мВ до –0,5 мВ, поэтому мы выделяем только те минимальные, скажем так экстремумы, минимальные значение сигнала, которые лежат в этих пределах. Также можно построить Q-зубцы на том же самом графике.

Как видите воспользовавшись двумя встроенными функциями мы успешно выделили Q-R-S комплекс из наших зашумленных и нестабильных по времени данных ЭКГ. В следующей публикации мы поговорим о корреляционной функции и корреляционной обработке.

Наверх

Корреляционная функция.

Когда мы рассматривали случайные процессы, мы упоминали корреляционную функцию, как меру изменения скорости процесса. КФ измерялась для одного сигнала, а значит происходило сравнение сигнала с самим собой, сдвинутым во времени. По факту мы рассматривали так называемую автокорреляционную функцию. Но в предыдущих видео мы не рассказали, как эта функция вычисляется. Для того, чтобы понять, как мы находим корреляционную функцию сигнала, надо вспомнить понятие корреляции.

Корреляция – это мера зависимости двух величин. Для численной оценки используется коэффициент корреляции. Он не может быть больше единицы, и меньше минус единицы. Когда коэффициент корреляции +1, говорят, что две величины идеально коррелированы друг с другом, а значит что при изменении первой величины на какой-то значение вторая изменяется на такое-же значение. Если коэффициент –1 , то росту первой величины соответствует уменьшение второй величины на такое же значение.

Проиллюстрируем зависимость коэффициента корреляции от временного сдвига двух идентичных сигналов.

В начальный момент времени сигналы выровнены, и коэффициент корреляции равен +1. При равном приращении первая и вторая функции изменяются одинаково. Теперь сдвинем вторую зависимость по времени.

При равном приращении она изменяется на меньшую величину. А значит, коэффициент корреляции между двумя зависимостями становится меньше. Увеличивая временной сдвиг мы доходим до момента, когда умен ьшение значения первой величины соответствует увеличению значения второй, а значит коэффициент корреляции становится отрицательным.

Зависимость коэффициента корреляции от временного сдвига между сигналами – по сути есть корреляционная функция. Но давайте рассмотрим формулу.

В общем случае мы рассматриваем взаимно-корреляционную функцию и оцениваем зависимость между двумя сигналами. Частным случаем взаимно-корреляционной функции является автокорреляционная функция, когда мы сравниваем сигнал с его задержанной во времени копией. 

Рассмотрим формулу. Я тут привёл формулу для непрерывных функций, но если мы берём дискретные величины, то операция интегрирования будет заменена на простое суммирование. Здесь есть две функции. Первая функция f (не обращайте пока что внимания на знак звёздочки, это комплексное сопряжение, но для действительных сигналов оно не важно), так вот, первая функция f умножается на вторую функцию g, при этом вторая функция сдвигается во времени на величину τ. От величины сдвига τ мы и строим зависимость коэффициента корреляции.

Рассмотрим графическое представление. Первую функцию f мы фиксируем на временной оси, а вторая g по этой оси будет перемещаться. Она перемещается из значений отрицательного сдвига между функциями в область положительных значений сдвига. Величина корреляции соответствует площади перекрытия двух графиков, и максимума она достигает, когда две фигуры максимально накладываются друг на друга. Стоит отметить, что если мы поменяем функции местами, то есть зафиксируем g и будем скользить функцией f, то вид корреляционной функции изменится на зеркальный. В случае автокорреляционной функции форма зависимости всегда симметрична, и имеет максимум в точке, равной нулевому сдвигу сигнала относительно самого себя.

Давайте посмотрим на несколько примеров подсчёта корреляционной функции для дискретных сигналов в MATLAB.

Автокорреляционная функция прямоугольного импульса имеет форму треугольника.

Взаимнокорреляционная функция пилообразного импульса и прямоугольного импульса несимметрична.

Автокорреляционная функция отрезка синусоиды симметрична, и имеет вид нарастающего и затухающего колебательного процесса с выраженным максимумом в моменте совпадения импульсов

А автокорреляционная функция бесконечной синусоиды – это такая же синусоида, с той же частотой.

Особо важно отметить автокорреляционную функцию случайного процесса, или шума. Она имеет один выраженный максимум, и при малейшем сдвиге значения её падают почти до нуля. Это говорит о том, что шум – слабо коррелированный процесс, и этим свойством мы будем пользоваться при обработке.

А обработка корреляционными методами – это важная часть ЦОС. При помощи вычисления взаимнокорреляционной функции  мы можем обнаруживать интересующие нас отрезки сигнала в эфире, в том числе на фоне шумов, находить сигналы, похожие на некий выбранный эталон, и оценивать степень схожести, или мы можем точно определять задержу распространения сигнала. К примеру, радиолокационная станция отправляет импульс известной формы в сторону цели и ждёт отражённый сигнал. Максимум корреляционной функции даст нам величину задержки между переданным и принятым импульсами, которую мы затем можем использовать для определения расстояния до цели.

Выполним корреляционную обработку сигнала в MATLAB. В данном случае мы будем пытаться найти фрагмент аудиосигнала в полном сигнале, в том числе на фоне шумов. Загружаемый аудиосигнал – эта запись звука кольца, крутящегося на столе. Давайте загрузим его и послушаем командой Sound. Так вот звучит фрагмент аудиосигнала, который мы попробуем найти. 

Область, которую мы выделили, обозначена на графике двумя пунктирными линиями. Давайте также построим график взаимной корреляционной функции исходного сигнала и выделенного фрагмента. Для этого воспользуемся функцией xcorr и передадим ей исходный сигнал и выделенный фрагмент.

В первую выходной переменной записываются отчёты функции, а во вторую – величины временного сдвига. На графике взаимной корреляционной функции мы видим явно выраженный максимум, в тот момент времени когда наш фрагмент совпадает с самим собой на исходном сигнале. Используем максимум вектора lags для того, чтобы отразить фрагмент на сигнале. 

Теперь давайте добавим шум к исходному сигналу и к фрагментам.

Причем, обратите внимание, что мы добавляем разный шум к полному сигналу и к нашему фрагменту. Послушаем как звучит фрагмент на фоне шума. Уровень шума достаточно велик, и мы совершенно не слышим звука кольца.

Но даже в этом случае корреляционная обработка позволяет нам точно определить момент начала фрагмента, и мы также сможем показать где наш искомый фрагмент на всём сигнале. Пока что закончим с корреляционной функцией и обработкой. Тема следующей публикации – моделирование сигнала, то есть приближение его аналитической функцией.

Введение

Чем более слабые сигналы приходится обрабатывать в цифровых системах связи, тем большее значение приобретают такие параметры, как уровень бит-ошибок, который непосредственно зависит от чувствительности тракта обработки сигнала и, конечно, коэффициента шума. Из перечисленных параметров коэффициент шума интересен в том плане, что его можно использовать не только как критерий оценки работы всей приемной системы в целом, но и как ключевую характеристику отдельных СВЧ-компонентов, таких как усилители и смесители, которые образуют эту систему. Если разработчик контролирует коэффициент шума и усиление отдельных каскадов приемной системы, то это означает, что он контролирует всю систему в целом. Если величина коэффициента шума известна, то рассчитать чувствительность всей системы, зная полосу обработки сигнала, не составит труда. Именно коэффициент шума — это зачастую тот параметр, который выгодно отличает одно приемное устройство от другого, один усилитель от другого, один транзистор от другого. Тот факт, что без использования понятия коэффициента шума сегодня сложно представить спецификацию на приемное устройство, подразумевает, что точность и повторяемость измерения данного параметра особенно важны при разработках и производстве СВЧ-устройств.

Измерение шумов некого электронного устройства — важная процедура для минимизации шума, генерируемого этим устройством в приемных системах. Основным способом снижения вероятности бит-ошибок при приеме и обработке цифровых потоков является усиление полезного сигнала электронными устройствами, которые имеют низкий уровень собственных шумов. Традиционные методы увеличения соотношения полезного сигнала к шуму заключаются, с одной стороны, в увеличении мощности сигнала, передаваемого в направлении приемника, а с другой — в увеличении усиления приемной антенны. Подобные способы связаны с известными трудностями, поскольку увеличение мощности сигнала передатчика ограничивается законодательно соответствующими контрольными органами, а увеличение усиления в антенне обычно связано с необходимостью разработки более дорогой и более громоздкой антенной системы. Альтернативным способом увеличения соотношения полезного сигнала к шуму является минимизация коэффициента шума приемной системы и ее компонентов. Таким образом, измерения коэффициента шума абсолютно необходимы, чтобы иметь уверенность в том, что шум, вносимый элементами приемной системы, допустимый.

Основная задача данной статьи — рассмотрение способов оценки коэффициента шума электронных устройств при помощи современных измерительных приборов. При этом мы покажем возможность измерения коэффициента шума при помощи анализатора спектра «СК4-БЕЛАН 32», который укомплектован соответствующей опцией.

Для четкого понимания смысла подобных измерений и правильной интерпретации их результатов необходимо напомнить, что скрывается под термином «коэффициент шума», а также что подразумевают связанные с ним понятия (эффективная шумовая температура, Y-фактор, избыточный коэффициент шума и т. д.).

Теория

Шум, с которым мы имеем дело на практике, состоит из многих составляющих. Основные из них — это тепловой и дробовой шумы. Тепловой шум возникает при флуктуациях электронов в проводниках, имеющих некую конечную температуру. Некоторые из таких флуктуаций могут иметь спектральные составляющие в той же полосе частот, что и полезные сигналы, то есть их маскировать и затруднять их обработку. Шумовой спектр, генерируемый тепловым шумом, по своей природе однороден на всех частотах. Дробовой шум возникает из-за квантовой стохастической природы электрического тока. Ток не представляет собой непрерывного и предсказуемого движения электронов, а скорее является хаотическим потоком со случайным их распределением. Статистический анализ стохастического потока электронов показывает, что вариации тока имеют широкополосный характер (распределены в широкой полосе частот). Есть и другие природные феномены, которые имеют квантовую структуру и генерируют случайный шум. Примером может служить шум генерации и рекомбинации основных носителей, возникающий в транзисторах при распределении тока эмиттера между базой и коллектором. Несмотря на многообразие источников шума, у всех механизмов генерации шума есть одно свойство, общее с тепловым шумом: они имеют однородный спектр, равномерно распределенный в полосе частот до 5000 ГГц. Поэтому при оценке шума все его источники принято рассматривать как тепловой шум. Мощность теплового шума определяется как:

где P_A — доступная мощность (Дж/с или Вт); k — постоянная Больцмана (1,38×10^–23 Дж/К); T — абсолютная температура (К); B — полоса частот (Гц).

Важно помнить, что k×T×B — это «доступная» мощность. То есть она «доступна» только при оптимальной (согласованной) нагрузке (если нет отражения энергии).

Определение k×T×B позволяет интуитивно лучше понять природу шума. Постоянная Больцмана k характеризует среднюю величину выделяемой кинетической энергии на единицу температуры. Присутствие в формуле температуры T предполагает, что с ее ростом выделяется больше мощности. Ну, и поскольку шум имеет широкополосную природу, в формуле мощности шума фигурирует B — используемая полоса частот.

Абсолютную температуру в 290 К (обычно обозначается как T₀) принято считать опорной величиной источников шума при измерениях коэффициента шума. Эта величина соответствует 16,8 °С и 62,3° по Фаренгейту. Спектральная плотность тепловых шумов k×T, генерируемая резистором на согласованную нагрузку в каждом герце электромагнитного спектра при данной температуре, равна 4×10^–21 Вт или –174 дБ·м.

Неотъемлемой частью определения коэффициента шума является понятие «соотношение сигнал/шум». Этот термин интуитивно понятен, особенно если перейти к логарифмическим соотношениям. Поясним данный термин на простом примере. Допустим, мы имеем сигнал (S) с уровнем 10 мВт (+10 дБ·м). Чему равно теоретическое соотношение «сигнал/шум», измеряемое в децибелах, для данного сигнала в полосе 1 МГц при температуре 290 К? Сначала рассчитаем мощность шума (N) в полосе 1 МГц:

Теперь вычислим соотношение «сигнал/шум»: S/N = (+10–(–114)) = 124 дБ.

Заметим, что соотношение «сигнал/шум» выражается просто в дБ. Хотя и мощность шума, и сигнал первоначально были в логарифмическом масштабе относительно 1 мВт.

Уяснив термин «соотношение сигнал/шум». мы можем перейти к определению понятия «коэффициент шума». Этот коэффициент описывает уменьшение соотношения «сигнал/шум» по мере прохождения сигнала через приемное устройство или его отдельный каскад (усилитель, смеситель). Фундаментальное определение коэффициента шума следующее:

где S_in / N_in — соотношение «сигнал/шум» на входе устройства; S_out / N_out — соотношение «сигнал/шум» на выходе устройства.

Поскольку все электронные устройства «шумят» и, соответственно, добавляют некое количество шума к сигналу, величина F всегда больше единицы. Хотя величина F исторически называлась коэффициентом шума, современный термин «коэффициент шума» (децибельная величина NF) обычно подразумевает логарифмический масштаб величины F, равный 10 log₁₀F (дБ). В зарубежной специальной литературе, публикуемой ведущими производителями измерителей коэффициента шума (Agilent Technologies, Anritsu, Rohde & Schwarz) последовательно разграничиваются два термина: «фактор шума», или F, и, собственно, коэффициент шума NF. Итак,

NF = 10 log₁₀×F                                                          (3).

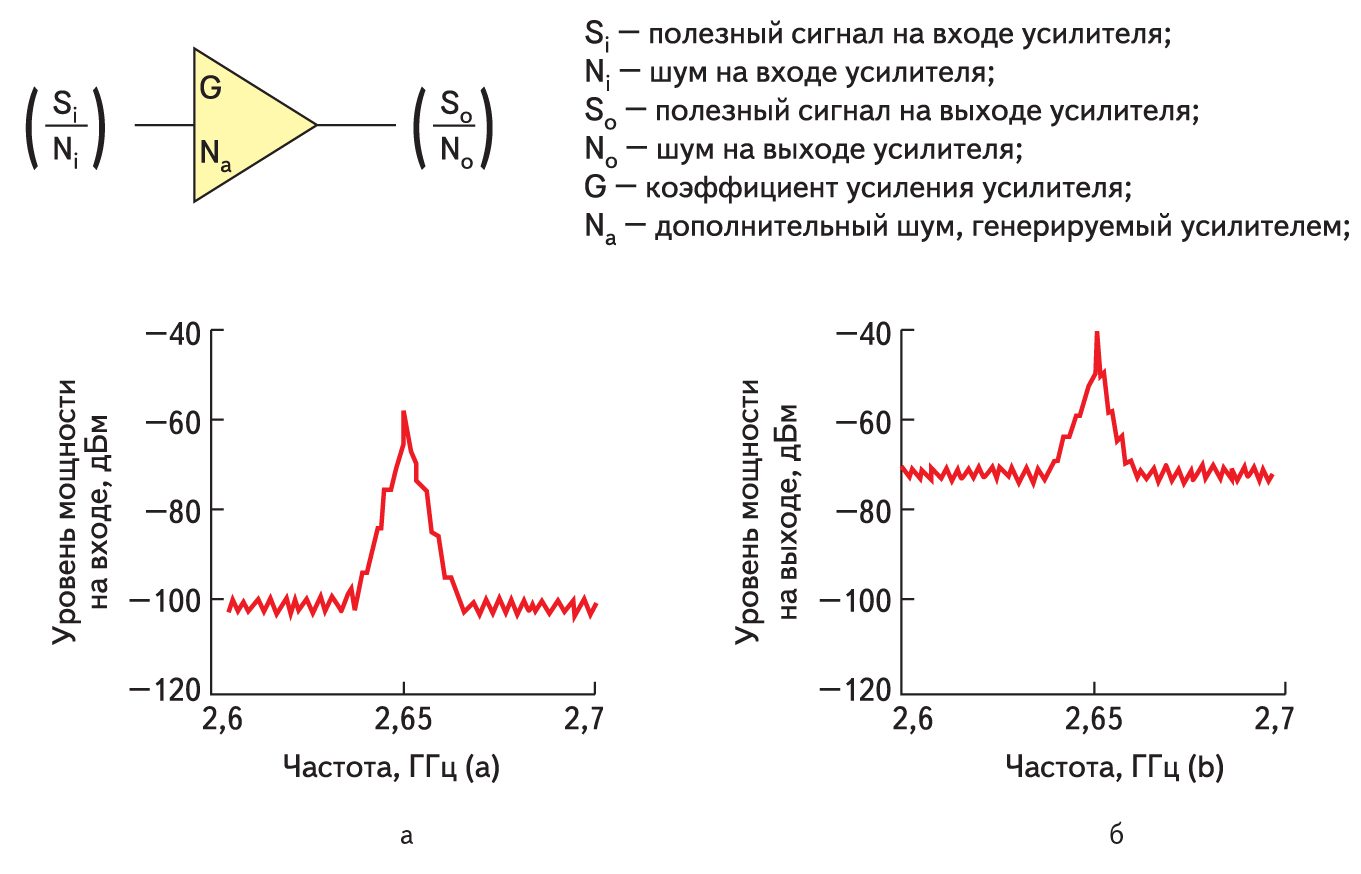
Рассмотрим коэффициент шума некоего известного усилителя. На рис. 1 показана его условная схема, а также сигналы на его входе и выходе.

Если мы подключим к входу усилителя согласованную нагрузку при температуре 290 К, то она будет генерировать на входе усилителя шум k×T₀×B. На выходе этот шум усилится и превратится в k×T₀×B×G (G — коэффициент усиления усилителя) плюс к нему добавится некое количество шума, генерируемого в самом усилителе N_A. Тогда выражение (2) можно переписать следующим образом:

отсюда:

или

Выражение (4) является определением коэффициента шума, которое официально принято международным Институтом Радиоинженеров (сейчас Institute of Electrical and Electronics Engineers (IEEE)).

Если опираться на уравнения (4) и (5), то видно, что измерения коэффициента шума сводятся к измерениям уровня шума, коэффициента усиления и полосы. Однако, несмотря на понятность данных величин, в практических измерениях формулами (4) и (5) пользуются не так уж часто (хотя использовать их можно, о чем мы расскажем ниже). Это связано с тем, что измерить с большой точностью усиление в заданной полосе — зачастую не тривиальная задача. Большинство систем измерения коэффициента шума элегантно обходят задачу прямого измерения уровня шума и усиления, основывая алгоритмы своей работы на использовании, в первую очередь, линейных свойств тепловых шумов.

Дело в том, что тепловой шум (P_A = k×T×B) в постоянной полосе частот имеет линейные характеристики. На рис. 2 представлен график функции мощности теплового шума от абсолютной температуры. Очевидно, что мощность шума — это линейная функция вида ƒ (x) = m×x+b, где ƒ (x) — это P_A , x — абсолютная температура T, m — переменная k×B, а b — это точка пересечения с осью Y, где при абсолютной температуре в 0 К мощность шума будет равна 0.

Таким образом, P_A(T) = k×B(T)+0 = k×B(T). При постоянной величине полосы, которая нам известна, это уравнение позволяет рассчитать мощность теплового шума для любой абсолютной температуры, то есть полностью описывает характеристики теплового шума. Поскольку прямая определяется двумя точками, то для описания характеристик теплового шума нам фактически лишь нужно взять две температурные точки и провести в них два измерения мощности шума. Если мы произведем измерение мощности на выходе некоего устройства (например усилителя), подключив к его входу согласованную нагрузку (генератор шума) при температуре T₀ = 290 K, то уравнение для мощности P₁ можно записать в таком виде:

Затем предположим, что мы нагрели согласованную нагрузку (включили генератор шума) до значения T_HOT = T₀+T_EX и снова измерили мощность P₂ на выходе усилителя. Уравнение для мощности P₂ будет иметь вид:

Отношение мощностей P₂ / P₁ исторически называется «Y-фактором» или Y (по-видимому, в связи с тем, что значения мощностей графически откладываются на оси Y — рис. 2).

Используя (4), получаем:

Или:

откуда находим, что фактор шума равен:

Величину T_EX/T₀ или (T_HOT–T₀)/T₀ обычно называют избыточным коэффициентом шума, или ENR (excess noise ratio), и производители источников шума нормируют ее в дБ. Формула (8) чаще записывается как:

в логарифмическом виде выражение для коэффициента шума имеет вид:

Часто при измерениях коэффициента шума может использоваться другое понятие, которое также является фундаментальным, — понятие «эффективной температуры шума». Любой инженер, занимающийся измерением коэффициента шума, должен четко понимать взаимосвязь понятий «коэффициент шума» и «температура шума».

Что же такое температура шума? Если 50-омный резистор с температурой 290 К подключен к входу идеального (не имеющего шумов) приемника с сопротивлением входа 50 Ом (рис. 3), то мощность шума на входе такого виртуального приемника составит:

А теперь представьте себе тестируемое устройство, например усилитель, подключенный в разрыв между 50-омным резистором и идеальным приемником (рис. 4).

Шум на выходе тестируемого устройства теперь включает две составляющие. Одна из них — это усиленный шум резистора с температурой 290 К. Другая составляющая — это шум, генерируемый самим тестируемым устройством. Обратите внимание, что приемник не может различить эти две составляющие шума. Для приемника результат измерения был бы тем же, если бы тестируемое устройство было идеально и не генерировало шума, а резистор, подключенный к входу устройства, был нагрет до некоторой более высокой температуры (290+T_e ) К. В сущности, реальное тестируемое устройство может быть промоделировано как идеальное устройство, не вносящее шума, но имеющее на входе дополнительный источник шума с эквивалентной температурой T_e. Это — эффективная температура шума тестируемого устройства (или эквивалентная температура шума тестируемого устройства).

Преимущество понятия эффективной температуры шума заключается в том, что это понятие подводит общее основание под измерения случайного электрического шума, генерируемого любым источником: от транзистора на основе технологии GaAs до галактики. Есть много разновидностей электрического шума, и большинство из них не имеют тепловой природы. Однако все виды случайного шума можно выразить как эквивалентное количество теплового шума, который генерировался бы при температуре T_e. Обычно слово «эффективная» или «эквивалентная» в сочетании с «температурой шума» опускается и традиционно употребляется выражение «температура шума».

Поскольку мощность теплового шума P_А прямо пропорциональна температуре T (что следует из уравнения (1)), то значения температуры шума можно складывать, точно так же, как значения мощности шума при условии, что полоса B не меняется.

Дополнительно прояснить понятие температуры шума можно при помощи графического представления функции мощности шума от температуры (рис. 5).

График 1 (рис. 5) представляет собой функцию мощности шума некоего реального усилителя. Обратите внимание, что T_e — это экстраполированная в минус точка пересечения графика с температурной осью, а также что усилитель вносит собственный шум N_A . На выходе данного усилителя при температуре T₀ можно будет детектировать мощность, равную N₁. Теперь сместим график 1 вправо на величину T_e и получим график 2 (рис. 5). График 2 — это график мощности на выходе идеального усилителя, не вносящего собственных шумов (мощность шума при нулевой температуре равна нулю) с неизменным значением переменной k×B×G (усиление и полоса константны, так же, как и постоянная Больцмана). Однако видно, что данный усилитель имеет на выходе ту же самую мощность шума N₁. Таким образом, на выходе идеального усилителя можно получить ту же самую мощность, что и у реального усилителя, если источник шума на входе идеального усилителя «нагреть» на величину T_e. Обратите внимание, что увеличение мощности на выходе идеального усилителя, вызванное «нагревом» источника шума, точно соответствует вносимому шуму N_A исходного реального усилителя. Следовательно:

Связь между фактором шума (коэффициентом шума) и температурой шума описывается следующим выражением:

или

В таблице даны некоторые значения для F, NF и T_e. Можно запомнить, что 0,1 дБ приблизительно соответствует 7–7,5 K.

Перед тем как перейти к практике измерений коэффициента шума, совершенно необходимо коснуться еще одного теоретического аспекта — определения коэффициента шума и температуры шума в многокаскадных системах. На рис. 6 показано, как генерируется шум в многокаскадной системе.

Шум на входе показан как резистор с температурой T₀. Каждый каскад характеризуется своей полосой B, усилением G и вносимым шумом N_А. Фактор шума системы задается следующим уравнением:

и для двухкаскадной системы:

Выражения (13) и (14) обычно называются каскадной формулой Харальда Фриса. Обратите внимание на то, что полоса B не фигурирует в уравнениях (13) и (14). Это демонстрирует преимущество методов, основывающихся на понятиях коэффициента шума и температуры шума: они не зависят от полосы.

Величина [(F₂–1)/G₁] в уравнении (13) часто называется эффектом второго каскада. Если усиление в первом каскаде большое, то эффект второго каскада будет минимальным, так что общий фактор шума F₁₂ будет определяться фактором шума первого каскада F₁. Вот почему приемник с высокой чувствительностью практически всегда начинается с малошумящего усилителя с малым коэффициентом шума (с предварительного усилителя).

Уравнение (14) можно переписать таким образом, чтобы найти F₁, если другие значения известны:

Это же уравнение, выраженное через температуру шума, имеет вид:

Уравнения (15) и (16) являются основой для большинства автоматических анализаторов коэффициента шума и прочих подобных приборов. Тестируемое устройство всегда является первым каскадом, а прибор, к входу которого подключается тестируемое устройство, является вторым каскадом.

Окончание статьи

Отношение сигнал/шум — один из важнейших факторов, определяющих качество работы любой радиотехнической системы. Для сетей кабельного телевидения (СКТ, по терминологии нового ГОСТа) этот параметр тем более важен, что он является фактически единственной доступно измеряемой величиной, характеризующей качество работы всей системы в целом. Согласитесь, что честно измерить CTB/CSO на реальной сети средствами кабельных операторов практически невозможно.

Вместе с тем, когда речь заходит о расчетах отношения сигнал/шум, понятии коэффициента шума прибора, шумовых характеристиках оптических трактов, как правило, наблюдаются полнейшая неразбериха и путаница. Вызвано это, по всей видимости, тем, что в нашей литературе отсутствует четкое и последовательное изложение перечисленных вопросов применительно к телевизионным сетям, а искать ответы, переворачивая горы литературы, не каждому по силам, да и времени на все не хватает. Поэтому мы решили попытаться прояснить эти понятия, чтобы у читателя возникла ясное и однозначное представление о том, что же происходит на самом деле. Настоящая статья отнюдь не претендует на глубокое исследование вопроса или какую-то особую новизну и многим специалистам она покажется весьма банальной — в ней говорится о хорошо известных вещах. Мы лишь попытались сконцентрировать накопленный опыт, чтобы помочь тем, кто испытывает дискомфорт от недостаточно ясного понимания проблемы. Цель данной работы — обратить внимание специалистов на некоторые нюансы классического расчета шумов и возникающие при этом заблуждения.

1. Понятия коэффициента шума и собственного шума устройства.

Каждый элемент сети в большей или меньшей степени генерирует электрический шум. Электроны в проводнике находятся в хаотическом температурном движении, поэтому на каждом сопротивлении, в каждом проводящем канале полевого транзистора возникает так называемый температурный (тепловой) шум сопротивления — белый шум, который равномерно распределен по всем частотам. Статистический (случайный) характер тока, текущего через p-n потенциальный барьер в полупроводниковых диодах и транзисторах, приводит к образованию так называемого дробового шума. Генерация и рекомбинация электронов и дырок в полупроводнике также имеет случайный характер и создает шум генерации-рекомбинации. При исследовании шумов в любой радиотехнической системе, в том числе в сети кабельного телевидения, все шумы (тепловые, дробовые, рекомбинационные), возникающие в отдельных элементах сети — усилителях, конверторах, кабелях, пассивных элементах — учитываются введением универсального параметра, определяемого для каждого элемента — коэффициента шума прибора. Зная эти коэффициенты (из каталогов) для всех входящих в систему составляющих и входное отношение сигнал/шум, можно однозначно определить отношение сигнал/шум на выходе. Учитывая важность этого параметра для дальнейшего изложения, остановимся подробнее на его определении и некоторых связанных с ним заблуждениях.

Определение термина «коэффициент шума» приводится практически в каждом учебнике по радиотехнике и устройствам СВЧ. Но в литературе он определяется по-разному. Очень широкое распространение получило определение коэффициента шума как показателя ухудшения отношения сигнал/шум на выходе прибора по сравнению с этим отношением на его входе. Т.е. коэффициент шума определяется здесь как отношение:

, (1.1)

или, в логарифмических единицах (дБ),

. (1.2)

Во многих учебниках и справочниках определение коэффициента шума на этом, к большому сожалению, и заканчивается, что приводит в дальнейшем к путанице и недоразумениям.

Действительно, допустим, мы принимаем с эфирной антенны ТВ-программу с отношением сигнал/шум, равным 60 дБ (померили прибором на выходе антенны), и подаем ее на усилитель головной станции, имеющий коэффициент шума 6 дБ (по каталогу). На выходе этого усилителя мы вроде бы должны получить отношение сигнал/шум в 54 дБ, как следует из вышеприведенного определения. В действительности же мы получаем практически те же 60 дБ, что и на входе. Это происходит вследствие того, что в приведенном определении опущена очень существенная оговорка, что под входным отношением сигнал/шум понимается отношение «чистого» (не содержащего шума) сигнала к (только!) тепловому шуму, создаваемому подключенным к входу устройства согласованному сопротивлению, в качестве которого должно выступать выходное сопротивление генератора этого самого сигнала. Таким образом, речь здесь идет не о реальных значениях сигналов и шумов на входе и выходе, а о весьма искусственных величинах, что сводит на нет красоту и лаконичность приведенного определения.

Мы воспользуемся несколько иным определением коэффициента шума. Это определение приводится в ряде серьезных учебников, а также в Большой Советской энциклопедии и более физично по своей сути. Ниже будет показано, что оба эти определения (с указанной оговоркой) эквивалентны.

Под коэффициентом шума F устройства при температуре T будем понимать отношение полной мощности всех шумов на выходе этого устройства в полосе измерения Df к выходной мощности шумов такого же идеального (нешумящего) устройства в той же полосе при условии, что единственный источник входного шума в обоих случаях — тепловой шум согласованного сопротивления, подключенного к входу устройства и находящегося при температуре T.

Это определение не так лаконично и, может быть, и не так наглядно как предыдущее, но зато гораздо более корректно. Отметим попутно еще одну маленькую, но важную деталь. Речь здесь идет о тепловом шуме, создаваемом именно внешним, подключаемым к входу сопротивлением, а не входным (внутренним) сопротивлением устройства, как указывается в некоторой литературе. Т.е. устройство представляется в виде черного ящика без внутренней структуры. Это очень важно иметь в виду, особенно при рассмотрении каскадирования устройств. В противном случае неизбежно возникнет путаница при выводе формул.

Если обозначить через K коэффициент передачи устройства (будем считать его постоянным в полосе измерения), а через nt — мощность теплового шума согласованного сопротивления на входе в полосе Df при температуре T, то для идеального (нешумящего) устройства мощность выходного шума будет равна ntK и коэффициент шума в соответствии с определением запишется как:

, (1.3)

где N_out — полная мощность всех шумов на выходе устройства в полосе Df.

Для предотвращения путаницы в дальнейшем сразу оговоримся, что здесь и ниже мы используем линейные единицы. При переходе к логарифмическим величинам мы это будем специально оговаривать и вводить индекс _(lg), как это сделано в формуле (1.2).

Полную мощность шума на выходе можно представить в виде суммы усиленного (если, допустим, речь идет об усилителе) входного теплового шума n_tK и собственного шума устройства N^o, тогда можно записать:

, (1.4)

откуда можно выразить собственный шум устройства через его коэффициент шума:

. (1.5)

Заметим, что эти формулы справедливы для любого устройства, не обязательно усилителя.

Собственный шум — это параметр, эквивалентно описывающий шумовые характеристики устройства. В ряде случаев, особенно при расчете большого числа каскадно соединенных устройств пользоваться им удобнее, чем коэффициентом шума. В литературе можно встретить эквивалентное определение собственного шума, приведенного к входу устройства, n^o. Физически приведенный к входу собственный шум можно рассматривать как добавку к тепловому входному шуму, в результате которой на выходе устройства получается полный выходной шум: N_out = (n_t + n^o)K. Связь между n^o и N^o очевидна: N^o = n^oK, поэтому (1.5) перепишется в виде:

. (1.5)

Мощность теплового шума согласованного сопротивления в полосе Df выражается известной формулой Найквиста:

, (1.6)

где

k = 1,38·10-23 Вт·с/К — постоянная Больцмана,
T — температура сопротивления, К,
Df — полоса измерения, Гц.

Для принятого у нас стандарта телевизионного вещания шумовая полоса выбирается равной 5.75 МГц, поэтому при стандартной температуре T = 293 K (20°C) получим nt = 2.32·10^-14 Вт или, в логарифмических единицах, n_t(lg) = 2.41 дБмкВ (ниже мы специально остановимся на связи мощности и напряжения в логарифмических единицах).

Из определения приведенного к входу собственного шума no, связи его с коэффициентом шума (1.5) и формулы Найквиста (1.6) вытекает еще один (уже третий!) альтернативный параметр для описания шумовых свойств устройства — его шумовая температура: Т_ш = (F — 1)T. Для идеального (нешумящего) устройства его Т_ш = 0.

Коэффициент шума — величина, которая может зависеть как от частоты, так и от температуры. Как правило, с ростом частоты и температуры она возрастает. В каталогах обычно приводится худшее значение этого параметра в рабочем частотном диапазоне при комнатной температуре. Зависимость коэффициента шума от температуры связана в основном с тепловыми шумами прибора, а от частоты — с шумами дробовыми и рекомбинации. Однако, в расчетах, как правило, эти зависимости не учитываются.

Покажем теперь эквивалентность приведенных определений коэффициента шума. Пусть на вход устройства подключено согласованное сопротивление, обеспечивающее тепловой шум n_t и действует какой-то сигнал C_in. Домножим числитель и знаменатель в (1.3) на C_in, получим:

,

что совпадает с формулой (1.1).

В заключение этого раздела заметим, что понятие коэффициента шума применимо не только к активным элементам сети, но и вообще к любому устройству, представляемому в виде четырехполюсника. Можно легко показать, что для пассивного устройства, имеющего затухание L > 1 (и, соответственно, коэффициент передачи K = 1/L <1) коэффициент шума численно равен этому затуханию: F = L. Чем больше затухание в пассивном элементе сети, тем больше его коэффициент шума. Этот факт просто отражает затухание сигнала при прохождении его через пассивный четырехполюсник и не говорит о какой-то дополнительной генерации шума.

2.Коэффициент шума каскадированных устройств. Формула Фрииса.

Выше мы говорили о шумовых характеристиках отдельного устройства. В сетях кабельного телевидения сигнал, распространяясь от антенны к абоненту, последовательно проходит все элементы каждой ветви, т.е. по отношению к этому сигналу мы имеем каскадное включение устройств — усилителей, ответвителей, кабелей и т.п. Наша задача — определить шумовые свойства всей цепочки, зная характеристики каждого элемента.

Пусть мы имеем m каскадно включенных устройств, каждое их которых имеет собственный коэффициент передачи K_i, коэффициент шума F_i и все устройства между собой согласованы по входу и выходу, т.е. как это принято в телевидении имеют входной и выходной импеданс 75 Ом, что, как правило, всегда более-менее выполняется (рис.1). Пусть к входу первого элемента подключено согласованное сопротивление, обеспечивающее тепловой шум nt на входе нашей цепочки. В соответствии с принятым определением найдем коэффициент шума всей этой цепи.

Входной тепловой шум сопротивления, проходя последовательно все элементы, будет усиливаться/ослабляться соответственно коэффициентам передачи устройств K_i и к нему будут добавляться собственные шумы всех этих устройств . Поэтому выходной шум нашей цепи будет равен:

. (2.1)

С другой стороны, если бы наша цепочка была идеальной (нешумящей), то выходной шум составил бы n_tK₁K₂…K_m. Отсюда в соответствии с определением (1.3) получим коэффициент шума каскадно включенных устройств:

откуда, вспоминая связь собственного шума и коэффициента шума (1.5):

,

сразу получим:

. (2.2)

Это известная формула, полученная Фриисом еще в 1944 г. Здесь обычно обращают внимание на то, что результирующий коэффициент шума определяется, в основном, шумами первого каскада, поскольку F₁ входит в формулу без знаменателя, тогда как остальные слагаемые имеют в знаменателях коэффициенты передачи входящих в цепочку устройств. Если бы речь шла исключительно о каскадировании усилителей, для которых, как правило, K_i>>1, то это было бы вполне справедливо. У нас же в качестве звеньев цепи выступают все устройства, образующие ветвь СКТ, как усилители, так и все пассивные элементы — ответвители, аттенюаторы, отрезки коаксиального кабеля, для которых, как уже говорилось выше, коэффициент шума численно равен затуханию и может быть весьма большим. Коэффициент же передачи в этом случае будет существенно меньше единицы. Из этого можно сделать вывод, что для улучшения шумовых свойств цепочки необходимо стремиться к тому, чтобы первый каскад был каскадом усиления с возможно бoльшим усилением и меньшим коэффициентом шума.

Приведем маленький пример. Пусть у нас антенна подключается к усилителю головной станции с коэффициентом шума F кабелем снижения с затуханием L. Т.е. мы имеем двухкаскадную систему, коэффициент шума которой по формуле Фрииса (2.2) будет равен:

,

или в децибелах:

.

И если коэффициент шума усилителя был, допустим, 10 дБ (не самый плохой усилитель), и затухание в кабеле снижения 10 дБ, то результирующий коэффициент шума системы будет 20 дБ, что уже, согласитесь, не так хорошо. Если же этот усилитель поставить на мачте до кабеля снижения, то результирующий коэффициент шума по формуле Фрииса получится равным 10,4 дБ, что при том же выходном уровне сигнала уже гораздо лучше. Поэтому при длинных спусках очень полезно использовать мачтовые антенные усилители. Здесь же стоит обратить внимание на следующее. Обычно в телевизионных усилителях перед собственно схемой усиления производители устанавливают аттенюатор и эквалайзер для выравнивания спектра входного сигнала. Коэффициент же шума усилителя, обозначенный в каталоге, приводится без учета этих деталей на входе — точнее, молчаливо предполагается, что они находятся в положении максимального пропускания. Как только мы начинаем пользоваться входными регулировками, у нас сразу же возрастает коэффициент шума. Установили аттенюатор на 10 дБ — на 10 дБ вырос коэффициент шума! Об этом также необходимо помнить и учитывать это при расчетах сетей. Именно по этой причине в хороших усилителях на входе добавляют каскад предусиления и только после него устанавливают регулируемые аттенюатор и эквалайзер.

3. Расчет выходного отношения сигнал/шум в прямом канале.

Конечной целью расчета телевизионной сети по шумовым параметрам в прямом канале является определение итогового отношения сигнал/шум у абонента. В данном разделе будем исходить из того, что в нашей сети имеется единственный источник сигнала — головная телевизионная станция. В принципе, возможна ситуация, когда к абоненту поступают сигналы от нескольких источников. Допустим, к сигналу, формируемому центральной головной станцией, на каком-то этапе подмешиваются сигналы местных телевизионных студий. Расчет шумов в этом случае сводится к суммированию шумов от всех источников в полосе сигнала и имеет некоторую специфику, на которой мы здесь останавливаться не будем. Предположим, что источник сигнала всего один, что справедливо для большинства практических случаев.

Перед тем как приступать к дальнейшему изложению, давайте определим, что же мы понимаем под сигналом, шумом и отношением сигнал/шум в телевизионных кабельных сетях. Мы не заостряли внимания на этом вопросе, считая это интуитивно понятным. На самом же деле, как показывает опыт общения с операторами, проектировщиками и инженерно-техническим персоналом СКТ, каждый понимает эти моменты по-своему, в результате чего происходят разночтения и казусы в подходах и трактовке результатов.

Прежде всего, отметим, что телевизионная сеть — это радиочастотная система, работающая с высокочастотными сигналами, т.е. с несущими, модулированными низкочастотными видеосигналами. Поэтому, говоря об отношении сигнал/шум применительно к системам СКТ, всегда имеют в виду именно отношение мощности высокочастотного сигнала (несущей) к шуму, а не отношение видеосигнал/шум. Это находит отражение и в обозначениях, используемых в формулах. Отношение сигнал/шум в СКТ принято обозначать как C/N или CNR (Carrier to Noise Ratio), т.е. несущая/шум, в то время как для видеосигнала отношение сигнал/шум обозначают S/N или SNR (Signal to Noise Ratio). Для того, чтобы не путать эти понятия и чтобы было ясно, что речь идет о высокочастотном сигнале, мы в дальнейшем будем пользоваться термином несущая/шум. С другой стороны, качество изображения на телевизоре абонента определяется как раз демодулированным видеосигналом, поэтому представляет большой интерес связь между отношениями сигнал/шум на радио- и видеочастотах. Это довольно непростой вопрос, связанный с используемым телевизионным стандартом, глубиной модуляции, алгоритмом работы демодулятора и схем обработки сигнала в телевизоре, а также с особенностями человеческого зрения — они учитываются так называемой процедурой «взвешивания» шума путем добавления в измерительный тракт «взвешивающего фильтра», отражающего частотную зависимость нашего восприятия шума на экране. Мы не будем останавливаться подробно на этой проблеме, отметим лишь, что в литературе встречаются различные данные на этот счет — обычно предполагается, что взвешенное отношение S/N на 1.5-3 дБ выше соответствующего отношения C/N.

Если посмотреть на спектр высокочастотного аналогового телевизионного сигнала, точнее, на спектр его яркостной составляющей, то мы увидим, что почти вся мощность этого сигнала сосредоточена вблизи несущей — более 90% в полосе 1 МГц. Поэтому за уровень аналогового сигнала в сетях кабельного телевидения принято принимать эффективное напряжение немодулированной несущей. Средняя мощность за период этой немодулированной несущей будет тогда практически соответствовать полной мощности высокочастотного телевизионного аналогового сигнала. Для всевозможных расчетов в СКТ удобнее уровни сигналов выражать в логарифмических единицах, поскольку тогда практически все вычисления сводятся к операциям сложения-вычитания. Обычно за сигнал с нулевым уровнем принимают сигнал с действующим напряжением U₀ = 1 мкВ, а уровень реального сигнала определяют как 20lg их отношения:

, [дБмкВ],

где U — действующее значение немодулированной несущей реального сигнала.

Действующее значение немодулированной несущей измеряется в реальном сигнале в момент передачи синхроимпульса (разумеется, для негативной модуляции несущей, принятой в большинстве стран).

Аналогично можно ввести логарифмические единицы для уровня мощности высокочастотного сигнала, определив его как 10lg отношения мощности сигнала к опорной мощности P₀. Если теперь за опорную мощность принять мощность, выделяемую на сопротивлении R = 75 Ом сигналом с действующим напряжением 1 мкВ, то в логарифмических единицах уровни сигнала, выражаемые через напряжения и через мощности, будут совпадать:

, [дБмкВ].

Таким образом, мы видим еще одно очень ценное качество логарифмического представления уровня сигнала — совершенно не надо задумываться, о чем идет речь — напряжении или мощности. Возникает одна универсальная величина — уровень. И когда мы говорим об отношении несущая/шум, мы вполне можем пользоваться нашими измерительными приборами, отградуированными в дБмкВ, понимая под измеренным значением мощность сигнала, поскольку логарифмические единицы на самом деле являются величинами безразмерными. Здесь же можно коснуться и работы спектроанализатора. Обычно спектроанализатор измерителя ТВ-сигналов имеет полосу измерения 1МГц, в которой, как уже говорилось, вблизи несущей сосредоточена практически вся мощность сигнала. Поэтому уровень несущей на экране спектроанализатора, отградуированного в дБмкВ, будет совпадать с измеренным уровнем сигнала в режиме просмотра изображения, когда происходит измерение действующего напряжения несущей во время синхроимпульса.

Перейдем теперь к понятию уровня шума. Если взглянуть на экран спектроанализатора, то наряду с пичками от аналоговых ТВ-сигналов мы увидим более-менее равномерный во всем частотном диапазоне шумовой «забор», образующий как бы фундамент для полезных сигналов. Но уровень этого «забора» отнюдь не обозначает уровень шума, который входит в отношение несущая/шум. Не надо забывать, что спектроанализатор показывает нам не абсолютную величину мощности или уровня сигнала, а его спектральную плотность, т.е. мощность, приходящуюся на полосу измерения спектроанализатора. Реальный уровень телевизионного сигнала мы наблюдаем на экране только потому, что полоса измерения телевизионного спектроанализатора выбирается, как правило, 1 МГц, и практически вся мощность аналогового ТВ-сигнала сосредоточена в этой полосе. Для любого другого более широкополосного сигнала, а уж тем более белого шума, это совсем не так. Для нахождения полной мощности широкополосного сигнала или шума необходимо проинтегрировать спектральную плотность в исследуемой частотной полосе. Поскольку спектральная плотность шума в полосе канала практически постоянна, то для определения реального уровня шума достаточно умножить ее на ширину шумовой полосы. Для отечественного телевизионного сигнала SECAM шумовая полоса, как уже отмечалось, принята равной 5.75 МГц. Поэтому для определения отношения несущая/шум, необходимо найти полную мощность шума в этой полосе. Для этого мы должны значение спектральной плотности шума (уровень того самого «забора») в [Вт/Гц] умножить на отношение шумовой полосы к полосе измерения спектроанализатора, т.е. 5,75МГц/1МГц. Поскольку спектроанализатор выдает значение спектральной плотности уже в логарифмических единицах, дБмкВ, то к этому значению мы просто должны добавить величину 10lg(5,75МГц/1МГц) = 7.6 дБ. Другими словами, если на экране спектроанализатора уровень нашего сигнала составляет 70 дБмкВ, а «уровень» шума — 30 дБмкВ, то отношение несущая/шум будет равно 32.4 дБ, а вовсе не 40 дБ, как многие ошибочно полагают.

Все, что было сказано выше об уровне шума, можно в полной мере отнести и к измерению уровня цифровых сигналов. Тот «уровень» цифровых пакетов, который мы наблюдаем на спектроанализаторе, вовсе не является настоящим уровнем, пригодным для проведения расчетов, а точно так же нуждается в пересчете в зависимости от реально занимаемой полосы. Например, когда говорят, что уровень цифровых пакетов должен быть на 10 дБ ниже уровня аналоговых сигналов, то для цифровых пакетов QAM, занимаемых полосу 6 МГц. Это означает, что на экране спектроанализатора разница между ними должна составлять 17.8 дБ (10 дБ + 10lg(6МГц/1МГц)).

После всех этих предварительных замечаний перейдем, наконец, к вычислению выходного отношения несущая/шум. Пусть нам заданы уровни несущей C_in и шума N_in на входе цепочки, состоящей из m последовательно соединенных устройств, каждое из которых характеризуется коэффициентом передачи K_i и коэффициентом шума F_i (рис.2). Наша задача — определить отношение C/N на выходе. Заметим, что под входным шумом N_in мы понимаем полный шум на входе цепочки, включая тепловой шум и все шумы, накопленные до этого. Т.е. тот реальный шум, который можно измерить.

Точно так же, как и при выводе формулы Фрииса (см. (2.1)) найдем уровень результирующего шума на выходе нашей цепи:

,

где — собственный шум i-го устройства.

Сигнал на выходе будет равен:

.

Деля одно на другое, получим:

.

Здесь мы ввели обозначение: C₁, C₂, …, C_m — выходные уровни сигналов соответственно на выходе 1-го, 2-го, …, m-го устройства.

Таким образом, мы получили хорошо известную формулу для вычисления выходного отношения несущая/шум в сетях кабельного телевидения:

, (3.1)

или, в логарифмическом виде:

. (3.2)

Очень важно иметь в виду, что в этих формулах, как следует из вывода, под отношением (C/N)_i понимается отношение несущей на выходе i-го устройства к собственному шуму этого устройства:

. (3.3)

Очень часто об этом забывают, опуская -1 в знаменателе и понимая под (C/N)_i отношение выходного сигнала к полному выходному шуму устройства, в котором кроме собственного шума присутствует еще и усиленный входной тепловой шум. Это приводит к ошибкам в расчетах, которые накапливаются при увеличении числа каскадов.

Формула (3.2) очень удобна для практических расчетов, поскольку оказывается, что для определения выходного отношения несущая/шум достаточно рассмотреть лишь прохождение сигнала вдоль трассы, а шумовые параметры, входящие в формулу, оказываются свойствами входящих в цепочку элементов и могут быть определены заранее. Не стоит только забывать, что в качестве элементов нашей цепи необходимо рассматривать все устройства, вплоть до отрезков кабеля и используемых входных аттенюаторов/эквалайзеров в усилителях, иначе расчет получится неверным.

Остановимся теперь на расчете отношения несущая/шум для сети, использующей оптический сегмент. В принципе, расчет здесь совершенно аналогичен, если рассматривать систему «оптический передатчик-приемник» как отдельное устройство, включенное в цепь прохождения сигнала. Есть только одна особенность. В отличие от остальных компонентов сети, имеющих определенные, приводимые в каталогах, значения коэффициента шума, для системы «оптический передатчик-приемник» производители такого параметра не дают, но приводят графики зависимости выходного отношения несущая/шум для системы «передатчик-приемник» в зависимости от мощности оптического излучения на входе приемника и количества используемых каналов. Возникает вопрос, как пользоваться такими графиками при расчетах? Для ответа на него, прежде всего, заметим, что при измерениях производитель оборудования использует на входе системы «чистые» сигналы с генератора, следовательно, входной шум обусловлен наличием только теплового шума на входе передатчика. С другой стороны, измеренные значения, представленные на графиках есть отношение несущей к полному шуму на выходе оптического приемника, т.е. к шуму, складывающемуся из усиленного входного теплового шума и собственного шума системы. Если воспользоваться найденным из графика значением и непосредственно использовать его в формуле (3.2), то мы совершим ту же ошибку, о которой говорилось касательно формулы (3.3). Поэтому, строго говоря, необходимо поступать следующим образом. Найдя из графика выходное отношение несущая/шум для нужного числа каналов в сети при имеющемся входном оптическом уровне на приемнике и зная расчетный уровень сигнала на выходе оптического приемника, определяем полную мощность шума на выходе. Далее определяем коэффициент передачи оптической системы как отношение сигнала на выходе приемника к сигналу на входе передатчика. По определению находим коэффициент шума системы (формула (1.3)) и подставляем все это в формулу (3.3). И только после этого можно использовать полученное для оптики значение C/N в формуле (3.2) для проведения дальнейших вычислений. Однако справедливости ради стоит заметить, что приведенная методика хотя и является более точной, дает не очень существенную для практического расчета поправку в итоговое отношение несущая/шум и ею, особенно при ручных расчетах, в принципе, можно пренебречь.

И, наконец, два слова о практических измерениях несущая/шум в сетях кабельного телевидения. Как уже говорилось в начале статьи, такие измерения — фактически единственная доступная оператору возможность объективного контроля качества сигнала. Все остальное — визуальная оценка на экране телевизора. И многие недорогие измерители уровня декларируют эту возможность. Как правило, алгоритм измерения заключается в следующем: пользователь выбирает канал, а прибор в автоматическом режиме меряет уровень несущей, затем отстраивается по частоте немного левее, за полосу канала, где, предположительно, никаких сигналов быть не должно, измеряет там уровень шума и, деля одно на другое, выдает результат. Насколько можно доверять этому результату? Боюсь разочаровать владельцев таких устройств, но доверять подобным измерениям мы бы очень не советовали. Во-первых, нет никакой гарантии, что там, куда прибор отстраивается, нет ничего, кроме шума. Там могут присутствовать какие-то помехи, «хвосты» от соседних каналов и бог знает что еще, что будет восприниматься устройством как шум и ошибочно измерено. Во-вторых, мы уже говорили о необходимости пересчета уровней в зависимости от измерительной полосы прибора и шумовой полосы сигнала. Причем, шумовая полоса для сигналов PAL и SECAM, строго говоря, разная. Заложен ли в приборе такой алгоритм пересчета? Ни в одном описании популярных на нашем рынке измерителей мы не находили этой информации. Ну и последнее, но самое главное. Уровень шума для измерения отношения C/N должен измеряться обязательно в полосе канала, а не за ее пределами! В противном случае можно говорить лишь о шумовых характеристиках самой сети, но никак не о качестве телевизионного сигнала, поскольку сигнал может быть сильно зашумлен уже до ввода его в сеть кабельного телевидения. Действительно, сигнал с эфирной антенны может достигать уровня более 100 дБмкВ и измеритель C/N при этом просто зашкалит, в то время как картинку на телевизоре из-за шумов смотреть будет невозможно. В то же время, если бы прибор измерял уровень шума в полосе канала, допустим, там, где сигнал яркости уже «закончился», а звук еще не «начался», то результат измерения был бы существенно другим. Вообще говоря, поскольку отношение сигнал/шум у лучших студийных камер не превышает, как правило, 60 дБ и в дальнейшем при распространении сигнала, разумеется, не улучшается, то говорить о каких-то величинах, больших этого значения, вообще не имеет смысла. В этом отношении гораздо корректнее работают приборы, которые меряют уже демодулированное отношение сигнал/шум. Они измеряют размах яркостного сигнала и взвешенный шум в какой-нибудь пустой строке, выбираемой автоматически или вручную и усредняя результат по нескольким измерениям. Достоверность такой методики оказывается, конечно, на порядок выше.

В заключение хотелось бы выразить особую благодарность Виталию Анатольевичу Германову за плодотворные дискуссии и важные замечания, оказавшие неоценимую помощь при подготовке данной работы.

From Wikipedia, the free encyclopedia

In signal processing, noise is a general term for unwanted (and, in general, unknown) modifications that a signal may suffer during capture, storage, transmission, processing, or conversion.^[1]

Sometimes the word is also used to mean signals that are random (unpredictable) and carry no useful information; even if they are not interfering with other signals or may have been introduced intentionally, as in comfort noise.

Noise reduction, the recovery of the original signal from the noise-corrupted one, is a very common goal in the design of signal processing systems, especially filters. The mathematical limits for noise removal are set by information theory.

Types of noise[edit]

Signal processing noise can be classified by its statistical properties (sometimes called the «color» of the noise) and by how it modifies the intended signal:

• Additive noise, gets added to the intended signal
  • White noise
    • Additive white Gaussian noise
  • Black noise
  • Gaussian noise
  • Pink noise or flicker noise, with 1/f power spectrum
  • Brownian noise, with 1/f² power spectrum
  • Contaminated Gaussian noise, whose PDF is a linear mixture of Gaussian PDFs
  • Power-law noise
  • Cauchy noise
• Multiplicative noise, multiplies or modulates the intended signal
• Quantization error, due to conversion from continuous to discrete values
• Poisson noise, typical of signals that are rates of discrete events
• Shot noise, e.g. caused by static electricity discharge
• Transient noise, a short pulse followed by decaying oscillations
• Burst noise, powerful but only during short intervals
• Phase noise, random time shifts in a signal

Noise in specific kinds of signals[edit]

Noise may arise in signals of interest to various scientific and technical fields, often with specific features:

• Noise (audio), such as «hiss» or «hum», in audio signals
  • Background noise, due to spurious sounds during signal capture
  • Comfort noise, added to voice communications to fill silent gaps
  • Electromagnetically induced noise, audible noise due to electromagnetic vibrations in systems involving electromagnetic fields
• Noise (video), such as «snow»
• Noise (radio), such as «static», in radio transmissions
• Image noise, affects images, usually digital ones
  • Salt and pepper noise or spike noise, scattered very dark or very light pixels
  • Fixed pattern noise, that is tied to pixel sensors
  • Shadow noise, made visible by increasing brightness or contrast
  • Speckle noise, typical of radar imaging and interferograms
  • Film grain in analog photography
  • Compression artifacts or «mosquito noise» around edges in JPEG and other formats
• Noise (electronics) in electrical signals
  • Johnson–Nyquist noise, in semiconductors
  • Quantum noise
  • Quantum 1/f noise, a disputed theory about quantum systems
  • Generation-recombination noise, in semiconductor devices
  • Oscillator phase noise, random fluctuations of the phase of an oscillator
  • Barkhausen effect or Barkhausen noise, in the strength of a ferromagnet
  • Spectral splatter or switch noise, caused by on/off transmitter switching
  • Ground noise, appearing at the ground terminal of audio equipment
• Synaptic noise, observed in neuroscience
• Neuronal noise, observed in neuroscience
• Transcriptional noise in the transcription of genes to proteins
• Cosmic noise, in radioastronomy
• Phonon noise in materials science
• Internet background noise, packets sent to unassigned or inactive IP addresses
• Fano noise, in particle detectors
• Mode partition noise in optical cables
• Seismic noise, spurious ground vibrations in seismology
• Cosmic microwave background, microwave noise left over from the Big Bang

Measures of noise in signals[edit]

A long list of noise measures have been defined to measure noise in signal processing: in absolute terms, relative to some standard noise level, or relative to the desired signal level. They include:

• Dynamic range, often defined by inherent noise level
• Signal-to-noise ratio (SNR), ratio of noise power to signal power
  • Peak signal-to-noise ratio, maximum SNR in a system
  • Signal to noise ratio (imaging), for images
  • Carrier-to-noise ratio, the signal-to-noise ratio of a modulated signal
• Noise power
• Noise figure
• Noise-equivalent flux density, a measure of noise in astronomy
• Noise floor
• Noise margin, by how much a signal exceeds the noise level
• Reference noise, a reference level for electronic noise
• Noise spectral density, noise power per unit of bandwidth
• Noise temperature
• Effective input noise temperature
• Noise-equivalent power, a measure of sensitivity for photodetectors
• Relative intensity noise, in a laser beam
• Antenna noise temperature, measure of noise in telecommunications antenna
• Received noise power, noise at a telecommunications receiver
• Circuit noise level, ratio of circuit noise to some reference level
• Channel noise level, some measure of noise in a communication channel
• Noise-equivalent target, intensity of a target when the signal-to-noise level is 1^[2]
• Equivalent noise resistance, a measure of noise based on equivalent resistor
• Carrier-to-receiver noise density, ratio of received carrier power to receiver noise
• Carrier-to-noise-density ratio,
• Spectral signal-to-noise ratio
• Antenna gain-to-noise temperature, a measure of antenna performance
• Contrast-to-noise ratio, a measure of image quality
• Noise print, statistical signature of ambient noise for its suppression
• Equivalent pulse code modulation noise, measure of noise by comparing to PCM quantization noise

Technology for noise in signals[edit]

Almost every technique and device for signal processing has some connection to noise. Some random examples are:

• Noise shaping
• Antenna analyzer or noise bridge, used to measure the efficiency of antennas
• Noise gate
• Noise generator, a circuit that produces a random electrical signal
• Radio noise source used to calibrate radiotelescopes
• Friis formulas for the noise in telecommunications
• Noise-domain reflectometry, uses existing signals to find cable faults
• Noise-immune cavity-enhanced optical heterodyne molecular spectroscopy

See also[edit]

• Anti-information
• Noise (electronics)
• Signal-to-noise statistic, a mathematical formula to measure the difference of two values relative to their standard deviations

References[edit]