Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
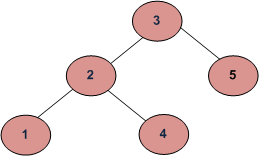
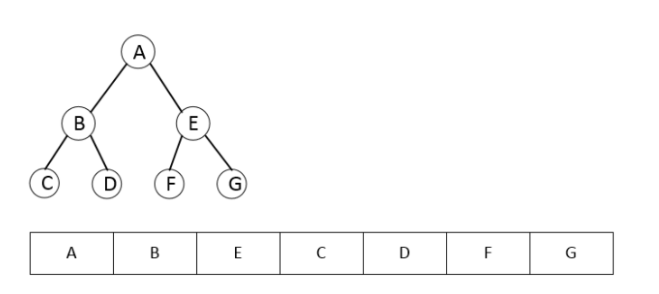
Given a Binary Tree and a key, write a function that returns level of the key.
For example, consider the following tree. If the input key is 3, then your function should return 1. If the input key is 4, then your function should return 3. And for key which is not present in key, then your function should return 0.
The idea is to start from the root and level as 1. If the key matches with root’s data, return level. Else recursively call for left and right subtrees with level as level + 1.
C++
#include <bits/stdc++.h>
using namespace std;
struct node {
int data;
struct node* left;
struct node* right;
};
int getLevelUtil(struct node* node, int data, int level)
{
if (node == NULL)
return 0;
if (node->data == data)
return level;
int downlevel
= getLevelUtil(node->left, data, level + 1);
if (downlevel != 0)
return downlevel;
downlevel = getLevelUtil(node->right, data, level + 1);
return downlevel;
}
int getLevel(struct node* node, int data)
{
return getLevelUtil(node, data, 1);
}
struct node* newNode(int data)
{
struct node* temp = new struct node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
int main()
{
struct node* root = new struct node;
int x;
root = newNode(3);
root->left = newNode(2);
root->right = newNode(5);
root->left->left = newNode(1);
root->left->right = newNode(4);
for (x = 1; x <= 5; x++) {
int level = getLevel(root, x);
if (level)
cout << "Level of " << x << " is " << level
<< endl;
else
cout << x << "is not present in tree" << endl;
}
getchar();
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int data;
struct node* left;
struct node* right;
} node;
int getLevelUtil(node* node, int data, int level)
{
if (node == NULL)
return 0;
if (node->data == data)
return level;
int downlevel
= getLevelUtil(node->left, data, level + 1);
if (downlevel != 0)
return downlevel;
downlevel = getLevelUtil(node->right, data, level + 1);
return downlevel;
}
int getLevel(node* node, int data)
{
return getLevelUtil(node, data, 1);
}
node* newNode(int data)
{
node* temp = (node*)malloc(sizeof(node));
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
int main()
{
node* root;
int x;
root = newNode(3);
root->left = newNode(2);
root->right = newNode(5);
root->left->left = newNode(1);
root->left->right = newNode(4);
for (x = 1; x <= 5; x++) {
int level = getLevel(root, x);
if (level)
printf(" Level of %d is %dn", x,
getLevel(root, x));
else
printf(" %d is not present in tree n", x);
}
getchar();
return 0;
}
Java
class Node {
int data;
Node left, right;
public Node(int d)
{
data = d;
left = right = null;
}
}
class BinaryTree {
Node root;
int getLevelUtil(Node node, int data, int level)
{
if (node == null)
return 0;
if (node.data == data)
return level;
int downlevel
= getLevelUtil(node.left, data, level + 1);
if (downlevel != 0)
return downlevel;
downlevel
= getLevelUtil(node.right, data, level + 1);
return downlevel;
}
int getLevel(Node node, int data)
{
return getLevelUtil(node, data, 1);
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(3);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(4);
for (int x = 1; x <= 5; x++) {
int level = tree.getLevel(tree.root, x);
if (level != 0)
System.out.println(
"Level of " + x + " is "
+ tree.getLevel(tree.root, x));
else
System.out.println(
x + " is not present in tree");
}
}
}
Python3
class newNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def getLevelUtil(node, data, level):
if (node == None):
return 0
if (node.data == data):
return level
downlevel = getLevelUtil(node.left,
data, level + 1)
if (downlevel != 0):
return downlevel
downlevel = getLevelUtil(node.right,
data, level + 1)
return downlevel
def getLevel(node, data):
return getLevelUtil(node, data, 1)
if __name__ == '__main__':
root = newNode(3)
root.left = newNode(2)
root.right = newNode(5)
root.left.left = newNode(1)
root.left.right = newNode(4)
for x in range(1, 6):
level = getLevel(root, x)
if (level):
print("Level of", x,
"is", getLevel(root, x))
else:
print(x, "is not present in tree")
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int d)
{
data = d;
left = right = null;
}
}
public class BinaryTree {
public Node root;
public virtual int getLevelUtil(Node node, int data,
int level)
{
if (node == null) {
return 0;
}
if (node.data == data) {
return level;
}
int downlevel
= getLevelUtil(node.left, data, level + 1);
if (downlevel != 0) {
return downlevel;
}
downlevel
= getLevelUtil(node.right, data, level + 1);
return downlevel;
}
public virtual int getLevel(Node node, int data)
{
return getLevelUtil(node, data, 1);
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(3);
tree.root.left = new Node(2);
tree.root.right = new Node(5);
tree.root.left.left = new Node(1);
tree.root.left.right = new Node(4);
for (int x = 1; x <= 5; x++) {
int level = tree.getLevel(tree.root, x);
if (level != 0) {
Console.WriteLine(
"Level of " + x + " is "
+ tree.getLevel(tree.root, x));
}
else {
Console.WriteLine(
x + " is not present in tree");
}
}
}
}
Javascript
<script>
class Node
{
constructor(d) {
this.data = d;
this.left = null;
this.right = null;
}
}
let root;
function getLevelUtil(node, data, level)
{
if (node == null)
return 0;
if (node.data == data)
return level;
let downlevel
= getLevelUtil(node.left, data, level + 1);
if (downlevel != 0)
return downlevel;
downlevel
= getLevelUtil(node.right, data, level + 1);
return downlevel;
}
function getLevel(node, data)
{
return getLevelUtil(node, data, 1);
}
root = new Node(3);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(1);
root.left.right = new Node(4);
for (let x = 1; x <= 5; x++)
{
let level = getLevel(root, x);
if (level != 0)
document.write(
"Level of " + x + " is "
+ getLevel(root, x) + "</br>");
else
document.write(
x + " is not present in tree");
}
</script>
Output
Level of 1 is 3 Level of 2 is 2 Level of 3 is 1 Level of 4 is 3 Level of 5 is 2
Time Complexity: O(n) where n is the number of nodes in the given Binary Tree.
Auxiliary Space: O(n)
Alternative Approach: The given problem can be solved with the help of level order traversal of given binary tree.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
int printLevel(Node* root, int X)
{
Node* node;
if (root == NULL)
return 0;
queue<Node*> q;
int currLevel = 1;
q.push(root);
while (q.empty() == false) {
int size = q.size();
while (size--) {
node = q.front();
if (node->data == X)
return currLevel;
q.pop();
if (node->left != NULL)
q.push(node->left);
if (node->right != NULL)
q.push(node->right);
}
currLevel++;
}
return 0;
}
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(7);
root->right->right = newNode(6);
cout << printLevel(root, 6);
return 0;
}
Java
import java.util.LinkedList;
import java.util.Queue;
class Node {
int data;
Node left, right;
public Node(int item)
{
data = item;
left = null;
right = null;
}
}
class BinaryTree {
Node root;
public static int currLevel = 1;
int printLevelOrder(int X)
{
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
Node tempNode = queue.poll();
if (tempNode.data == X)
return currLevel;
if (tempNode.left != null)
queue.add(tempNode.left);
if (tempNode.right != null)
queue.add(tempNode.right);
}
currLevel++;
}
return currLevel;
}
public static void main(String args[])
{
BinaryTree tree_level = new BinaryTree();
tree_level.root = new Node(1);
tree_level.root.left = new Node(2);
tree_level.root.right = new Node(3);
tree_level.root.left.left = new Node(4);
tree_level.root.left.right = new Node(5);
tree_level.root.right.left = new Node(7);
tree_level.root.right.right = new Node(6);
System.out.println(
"Level order traversal of binary tree is - "
+ tree_level.printLevelOrder(6));
}
}
Python3
class Node:
def __init__(self, key):
self.data = key
self.left = None
self.right = None
def printLevel(root, X):
if root is None:
return 0
q = []
currLevel = 1
q.append(root)
while(len(q) > 0):
size = len(q)
for i in range(size):
node = q.pop(0)
if(node.data == X):
return currLevel
if node.left is not None:
q.append(node.left)
if node.right is not None:
q.append(node.right)
currLevel += 1
return 0
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(7)
root.right.right = Node(6)
print(printLevel(root, 6))
C#
using System;
using System.Collections.Generic;
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = null;
right = null;
}
}
public class BinaryTree {
Node root;
int printLevel(int X)
{
Node node;
if (root == null)
return 0;
Queue<Node> q = new Queue<Node>();
int currLevel = 1;
q.Enqueue(root);
while (q.Count != 0) {
int size = q.Count;
while (size-- != 0) {
node = q.Dequeue();
if (node.data == X)
return currLevel;
if (node.left != null)
q.Enqueue(node.left);
if (node.right != null)
q.Enqueue(node.right);
}
currLevel++;
}
return 0;
}
public static void Main()
{
BinaryTree tree_level = new BinaryTree();
tree_level.root = new Node(1);
tree_level.root.left = new Node(2);
tree_level.root.right = new Node(3);
tree_level.root.left.left = new Node(4);
tree_level.root.left.right = new Node(5);
tree_level.root.right.left = new Node(7);
tree_level.root.right.right = new Node(6);
Console.WriteLine(tree_level.printLevel(6));
}
}
Javascript
class Node
{
constructor(d) {
this.data = d;
this.left = null;
this.right = null;
}
}
let root;
let currLevel = 1;
function printLevelOrder(X){
let queue = [root];
while(queue[0]){
let size = queue.length;
for(let i=0;i<size;i++){
let tempNode = queue.shift();
if(tempNode.data==X){
return currLevel;
}
if(tempNode.left){
queue.push(tempNode.left);
}
if(tempNode.right){
queue.push(tempNode.right);
}
}
currLevel+=1;
}
return root.data;
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(7);
root.right.right = new Node(6);
console.log(printLevelOrder(6));
Time Complexity: O(n) where n is the number of nodes in the binary tree.
Auxiliary Space: O(n) where n is the number of nodes in the binary tree.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Last Updated :
21 Nov, 2022
Like Article
Save Article
#c #binary-tree #binary-search-tree
Вопрос:
Это код для поиска уровня при передаче уровня в качестве аргумента функции.
int findLevel(node* root, node* ptr,
int level = 0) {
if (root == NULL)
return -1;
if (root == ptr)
return level;
// If NULL or leaf Node
if (root->left == NULL amp;amp; root->right == NULL)
return -1;
// Find If ptr is present in the left or right subtree.
int levelLeft = findLevel(root->left, ptr, level 1);
int levelRight = findLevel(root->right, ptr, level 1);
if (levelLeft == -1)
return levelRight;
else
return levelLeft;}
Но как найти, не проходя уровень в качестве аргумента? Должен ли у меня быть уровень в структуре узла? Как же тогда его инициализировать?
Это моя структура и вставьте ее прямо сейчас:
typedef struct Node{
int value;
bst left;
bst right;
} node;
node* bst_insert (node* root, int value){
if(root == NULL){
root = (node*) malloc(sizeof(node));
root->value = value;
root->left = NULL;
root->right = NULL;
}
else{
if(value > root->value)
root->right = bst_insert(root->right, value);
else
root->left = bst_insert(root->left, value);
}
return root;
}
Ответ №1:
Ваш лучший вариант, вероятно, состоит в том, чтобы преобразовать ваш рекурсивный алгоритм в итеративную версию. Затем вы можете сохранить уровень в локальной переменной и отслеживать путь поиска с помощью стека (для первого поиска по глубине (DFS)).
Вы можете, как вы упомянули, хранить уровень в каждом узле, но технически это означает передачу его в качестве аргумента. При вставке вы устанавливаете уровень нового узла на уровень родительского 1. Вот минимальная реализация этой идеи:
#include <assert.h>
#include <stdlib.h>
struct node;
struct node {
int value;
int level;
struct node *left;
struct node *right;
};
struct node *node_new(int value, int level) {
struct node *n = malloc(sizeof(struct node));
assert(n);
n->value = value;
n->level = level;
n->left = 0;
n->right = 0;
return n;
}
void node_insert(struct node **current, int value) {
// leaf
struct node **next = value < (*current)->value ? amp;(*current)->left : amp;(*current)->right;
if(!*next) {
*next = node_new(value, (*current)->level 1);
return;
}
// non-leaf
node_insert(next, value);
}
int main() {
struct node *root = node_new(10, 0);
node_insert(amp;root, 5);
node_insert(amp;root, 20);
node_insert(amp;root, 30);
}
Комментарии:
1. Как это реализовать: «вы устанавливаете уровень текущего узла на уровень родительского 1»?
2. Исправьте свой bst_insert, чтобы подключать каждый новый узел к вашему дереву. Я бы переименовал root в current в вашем текущем коде. Указатель корневого узла обычно хранится в дереве структуры. Когда вы вставляете первый узел, вы замечаете, что ваш корневой узел равен нулю, поэтому вы устанавливаете уровень 0 (или 1 в зависимости от того, как вы хотите считать) в его узле. Затем при следующей вставке вы выясняете, идет ли новый лист влево и вправо, затем вы устанавливаете, например, current->left = malloc(размер(узел)) и current->>left->>>высота = current->>>>высота 1.
Бинарные деревья поиска и рекурсия – это просто
Время на прочтение
8 мин
Количество просмотров 524K
Существует множество книг и статей по данной теме. В этой статье я попробую понятно рассказать самое основное.
Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.
Рис. 1 Бинарное дерево
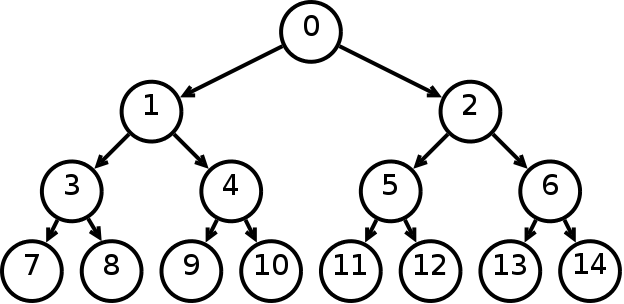
Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.
Рис. 2 Бинарное дерево поиска
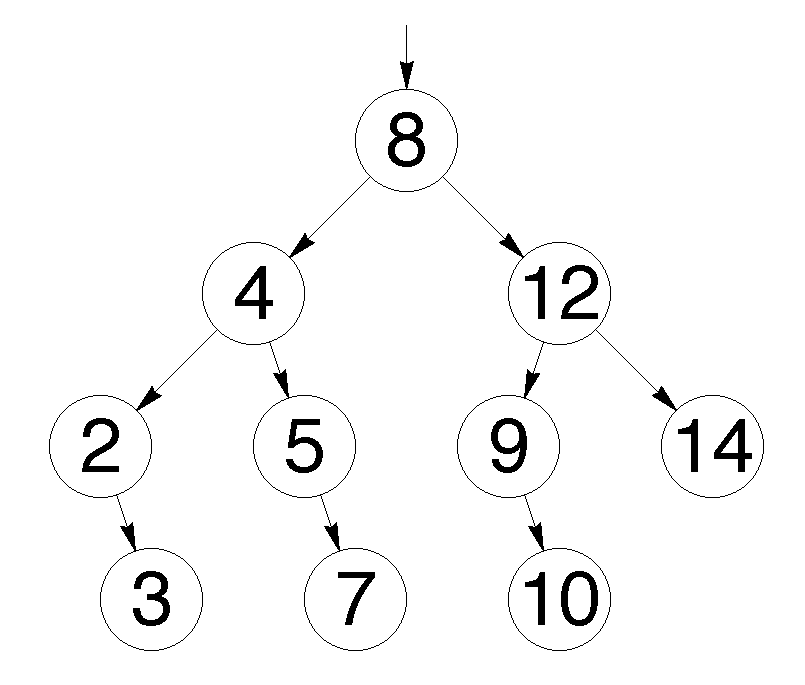
Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.
Рис. 3 Сбалансированное бинарное дерево поиска
Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.
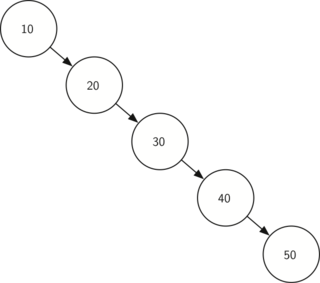
Рис. 4 Экстремально несбалансированное бинарное дерево поиска
Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO).
int factorial(int n)
{
if(n <= 1) // Базовый случай
{
return 1;
}
return n * factorial(n - 1); //рекурсивеый вызов с другим аргументом
}
// factorial(1): return 1
// factorial(2): return 2 * factorial(1) (return 2 * 1)
// factorial(3): return 3 * factorial(2) (return 3 * 2 * 1)
// factorial(4): return 4 * factorial(3) (return 4 * 3 * 2 * 1)
// Вычисляет факториал числа n (n должно быть небольшим из-за типа int
// возвращаемого значения. На практике можно сделать long long и вообще
// заменить рекурсию циклом. Если важна скорость рассчетов и не жалко память, то
// можно совсем избавиться от функции и использовать массив с предварительно
// посчитанными факториалами).
void reverseBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2;
reverseBinary(n/2); //рекурсивеый вызов с другим аргументом
}
// Печатает бинарное представление числа в обратном порядке
void forvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
forvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2;
}
// Поменяли местами две последние инструкции
// Печатает бинарное представление числа в прямом порядке
// Функция является примером эмуляции стека
void ReverseForvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2; // печатает в обратном порядке
ReverseForvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2; // печатает в прямом порядке
}
// Функция печатает сначала бинарное представление в обратном порядке,
// а затем в прямом порядке
int product(int x, int y)
{
if (y == 0) // Базовый случай
{
return 0;
}
return (x + product(x, y-1)); //рекурсивеый вызов с другим аргументом
}
// Функция вычисляет произведение x * y ( складывает x y раз)
// Функция абсурдна с точки зрения практики,
// приведена для лучшего понимания рекурсии
Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину.
Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO).
Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек.
С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна.
Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой.
DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности.
Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order).
Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции.
Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов.
Рис. 5 Вспомогательный рисунок для обходов
Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка.
struct TreeNode
{
double data; // ключ/данные
TreeNode *left; // указатель на левого потомка
TreeNode *right; // указатель на правого потомка
};
void levelOrderPrint(TreeNode *root) {
if (root == NULL)
{
return;
}
queue<TreeNode *> q; // Создаем очередь
q.push(root); // Вставляем корень в очередь
while (!q.empty() ) // пока очередь не пуста
{
TreeNode* temp = q.front(); // Берем первый элемент в очереди
q.pop(); // Удаляем первый элемент в очереди
cout << temp->data << " "; // Печатаем значение первого элемента в очереди
if ( temp->left != NULL )
q.push(temp->left); // Вставляем в очередь левого потомка
if ( temp->right != NULL )
q.push(temp->right); // Вставляем в очередь правого потомка
}
}
void preorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в прямом порядке.
// Вместо печати первой инструкцией функции может быть любое действие
// с данным узлом
void inorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
cout << root->data << " ";
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в симметричном порядке.
// То есть в отсортированном порядке
void postorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
}
// Функция печатает значения бинарного дерева поиска в обратном порядке.
// Не путайте обратный и обратноотсортированный (обратный симметричный).
void reverseInorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
}
// Функция печатает значения бинарного дерева поиска в обратном симметричном порядке.
// То есть в обратном отсортированном порядке
void iterativePreorder(TreeNode *root)
{
if (root == NULL)
{
return;
}
stack<TreeNode *> s; // Создаем стек
s.push(root); // Вставляем корень в стек
/* Извлекаем из стека один за другим все элементы.
Для каждого извлеченного делаем следующее
1) печатаем его
2) вставляем в стек правого! потомка
(Внимание! стек поменяет порядок выполнения на противоположный!)
3) вставляем в стек левого! потомка */
while (s.empty() == false)
{
// Извлекаем вершину стека и печатаем
TreeNode *temp = s.top();
s.pop();
cout << temp->data << " ";
if (temp->right)
s.push(temp->right); // Вставляем в стек правого потомка
if (temp->left)
s.push(temp->left); // Вставляем в стек левого потомка
}
}
// В симметричном и обратном итеративном обходах просто меняем инструкции
// местами по аналогии с рекурсивными функциями.
Надеюсь Вы не уснули, и статья была полезна. Скоро надеюсь последует продолжение
банкета
статьи.
Напишите эффективный алгоритм для вычисления высоты бинарного дерева. Высота или глубина бинарного дерева — это общее количество ребер или узлов на самом длинном пути от корневого узла до конечного узла.
Программа должна учитывать общее количество узлов на самом длинном пути. Например, высота пустого дерева равна 0, а высота дерева только с одним узлом равна 1.
Потренируйтесь в этой проблеме
Рекурсивное решение
Идея состоит в том, чтобы обойти дерево в мода на заказ и вычислить высоту левого и правого поддерева. Высота поддерева с корнем в любом узле будет на единицу больше, чем максимальная высота его левого и правого поддеревьев. Рекурсивно примените это свойство ко всем узлам дерева восходящим образом (пост-порядок) и верните максимальную высоту поддерева с корнем в этом узле.
Алгоритм может быть реализован следующим образом на C++, Java и Python:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
#include <iostream> using namespace std; // Структура данных для хранения узла бинарного дерева struct Node { int key; Node *left, *right; Node(int key) { this->key = key; this->left = this->right = nullptr; } }; // Рекурсивная функция для вычисления высоты заданного бинарного дерева int height(Node* root) { // базовый случай: пустое дерево имеет высоту 0 if (root == nullptr) { return 0; } // повторяем для левого и правого поддерева и учитываем максимальную глубину return 1 + max(height(root->left), height(root->right)); } int main() { Node* root = new Node(15); root->left = new Node(10); root->right = new Node(20); root->left->left = new Node(8); root->left->right = new Node(12); root->right->left = new Node(16); root->right->right = new Node(25); cout << «The height of the binary tree is « << height(root); return 0; } |
Скачать Выполнить код
результат:
The height of the binary tree is 3
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
// Класс для хранения узла бинарного дерева class Node { int key; Node left = null, right = null; Node(int key) { this.key = key; } } class Main { // Рекурсивная функция для вычисления высоты заданного бинарного дерева public static int height(Node root) { // базовый случай: пустое дерево имеет высоту 0 if (root == null) { return 0; } // повторяем для левого и правого поддерева и учитываем максимальную глубину return 1 + Math.max(height(root.left), height(root.right)); } public static void main(String[] args) { Node root = new Node(15); root.left = new Node(10); root.right = new Node(20); root.left.left = new Node(8); root.left.right = new Node(12); root.right.left = new Node(16); root.right.right = new Node(25); System.out.println(«The height of the binary tree is « + height(root)); } } |
Скачать Выполнить код
результат:
The height of the binary tree is 3
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# Класс для хранения узла бинарного дерева. class Node: def __init__(self, key=None, left=None, right=None): self.key = key self.left = left self.right = right # Рекурсивная функция для вычисления высоты заданного бинарного дерева def height(root): # Базовый случай: пустое дерево имеет высоту 0 if root is None: return 0 # повторяется для левого и правого поддерева и учитывает максимальную глубину return 1 + max(height(root.left), height(root.right)) if __name__ == ‘__main__’: root = Node(15) root.left = Node(10) root.right = Node(20) root.left.left = Node(8) root.left.right = Node(12) root.right.left = Node(16) root.right.right = Node(25) print(‘The height of the binary tree is’, height(root)) |
Скачать Выполнить код
результат:
The height of the binary tree is 3
Временная сложность приведенного выше рекурсивного решения равна O(n), куда n это общее количество узлов в бинарном дереве. Вспомогательное пространство, необходимое программе, равно O(h) для стека вызовов, где h это высота дерева.
Итеративное решение
В итеративной версии выполните обход порядка уровней на дереве. Тогда высота дерева равна общему количеству уровней в нем. Ниже приведена программа на C++, Java и Python, которая демонстрирует это:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
#include <iostream> #include <list> using namespace std; // Структура данных для хранения узла бинарного дерева struct Node { int key; Node *left, *right; Node(int key) { this->key = key; this->left = this->right = nullptr; } }; // Итерационная функция для вычисления высоты заданного бинарного дерева // путем обхода дерева по уровням int height(Node* root) { // пустое дерево имеет высоту 0 if (root == nullptr) { return 0; } // создаем пустую queue и ставим в queue корневой узел list<Node*> queue; queue.push_back(root); Node* front = nullptr; int height = 0; // цикл до тех пор, пока queue не станет пустой while (!queue.empty()) { // вычисляем общее количество узлов на текущем уровне int size = queue.size(); // обрабатываем каждый узел текущего уровня и ставим их в queue // непустые левый и правый потомки while (size—) { front = queue.front(); queue.pop_front(); if (front->left) { queue.push_back(front->left); } if (front->right) { queue.push_back(front->right); } } // увеличиваем высоту на 1 для каждого уровня height++; } return height; } int main() { Node* root = new Node(15); root->left = new Node(10); root->right = new Node(20); root->left->left = new Node(8); root->left->right = new Node(12); root->right->left = new Node(16); root->right->right = new Node(25); cout << «The height of the binary tree is « << height(root); return 0; } |
Скачать Выполнить код
результат:
The height of the binary tree is 3
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
import java.util.ArrayDeque; import java.util.Queue; // Класс для хранения узла бинарного дерева class Node { int key; Node left = null, right = null; Node(int data) { this.key = data; } } class Main { // Итерационная функция для вычисления высоты заданного бинарного дерева // путем обхода дерева по уровням public static int height(Node root) { // пустое дерево имеет высоту 0 if (root == null) { return 0; } // создаем пустую queue и ставим в queue корневой узел Queue<Node> queue = new ArrayDeque<>(); queue.add(root); Node front = null; int height = 0; // цикл до тех пор, пока queue не станет пустой while (!queue.isEmpty()) { // вычисляем общее количество узлов на текущем уровне int size = queue.size(); // обрабатываем каждый узел текущего уровня и ставим их в queue // непустые левый и правый потомки while (size— > 0) { front = queue.poll(); if (front.left != null) { queue.add(front.left); } if (front.right != null) { queue.add(front.right); } } // увеличиваем высоту на 1 для каждого уровня height++; } return height; } public static void main(String[] args) { Node root = new Node(15); root.left = new Node(10); root.right = new Node(20); root.left.left = new Node(8); root.left.right = new Node(12); root.right.left = new Node(16); root.right.right = new Node(25); System.out.println(«The height of the binary tree is « + height(root)); } } |
Скачать Выполнить код
результат:
The height of the binary tree is 3
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
from collections import deque # Класс для хранения узла бинарного дерева. class Node: def __init__(self, data, left=None, right=None): self.key = data self.left = left self.right = right # Итерационная функция для вычисления высоты заданного бинарного дерева #, выполняя обход по порядку уровней в дереве def height(root): # Пустое дерево # имеет высоту 0 if root is None: return 0 # создает пустую queue и ставит в queue корневой узел queue = deque() queue.append(root) height = 0 # Цикл # до тех пор, пока queue не станет пустой while queue: # вычисляет общее количество узлов на текущем уровне size = len(queue) # обрабатывает каждый узел текущего уровня и ставит их в queue. # непустые левый и правый потомки while size > 0: front = queue.popleft() if front.left: queue.append(front.left) if front.right: queue.append(front.right) size = size — 1 # увеличивает высоту на 1 для каждого уровня height = height + 1 return height if __name__ == ‘__main__’: root = Node(15) root.left = Node(10) root.right = Node(20) root.left.left = Node(8) root.left.right = Node(12) root.right.left = Node(16) root.right.right = Node(25) print(‘The height of the binary tree is’, height(root)) |
Скачать Выполнить код
результат:
The height of the binary tree is 3
Временная сложность приведенного выше итеративного решения равна O(n), куда n это общее количество узлов в бинарном дереве. Вспомогательное пространство, необходимое программе, равно O(n) для структуры данных queue.
Спасибо за чтение.
Пожалуйста, используйте наш онлайн-компилятор размещать код в комментариях, используя C, C++, Java, Python, JavaScript, C#, PHP и многие другие популярные языки программирования.
Как мы? Порекомендуйте нас своим друзьям и помогите нам расти. Удачного кодирования 
Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
***
В предыдущих статьях серии мы имели дело с довольно простыми линейными структурами данных. В них были начало и конец, а все элементы шли друг за другом и имели порядковый номер. Этой простоте приходит конец, когда мы выходим за пределы линии. Сегодня поговорим об очень важной структуре данных – деревьях – и алгоритмах для работы с ней.
Другие статьи цикла:
- Часть 1. Основные понятия и работа с массивами
- Часть 2. Стеки, очереди и связные списки
- Часть 4. Графы
- Часть 5. Объекты и хеширование
- Часть 6. Полезные алгоритмы для веб-разработки
Структура данных «Дерево»
В самом начале изучения деревья могут сбивать с толку, ведь они используют совсем другой способ упорядочивания данных – иерархический. Но хотя это и может показаться сложным, на практике это обычно оборачивается профитом, так как деревья позволяют применять более эффективные алгоритмы.
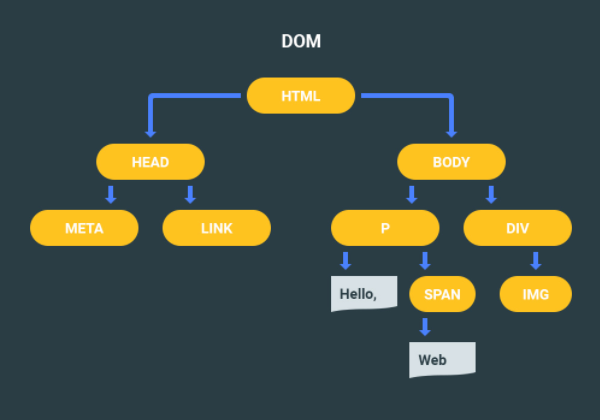
Структура дерево очень активно используется в разработке, например, всеми любимый DOM – это дерево. В виде дерева можно представить, например, иерархию должностей в компании или каталог библиотеки.
Устройство дерева
В отличие от обычных деревьев, структура данных дерево растет сверху вниз – ее корень находится на самом верху – так удобнее изображать.
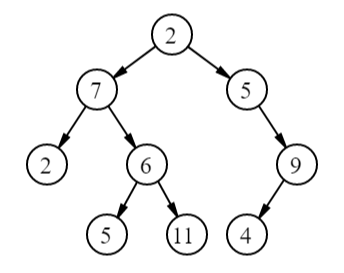
- У корневого элемента (на картинке узел со значением 2) есть несколько дочерних узлов (7 и 5), каждый из которых в свою очередь сам является корнем поддерева. Таких уровней может быть сколько угодно.
- Элемент, у которого нет дочерних узлов, называется листом, или терминальным узлом (2, 5, 11, 4). Все остальные узлы (кроме корневого), у которых есть потомки, называются внутренними.
- Каждый узел дерева имеет только одного родителя, не больше. Кроме корневого узла, у которого родителей нет вообще.
- Высота дерева – длина самой длинной ветви (количество ребер). У дерева на картинке она равна 3 – ветка от корня 2 до листа 5. Высоту также можно найти для любого внутреннего узла, например, для узла 6 высота равна 1.
Бинарные деревья
В общем случае число дочерних узлов в дереве не ограничено, но нас в основном интересуют деревья, узлы которых имеют не больше двух потомков (левый и правый). Такие деревья называются двоичными (бинарными) и широко используются во многих задачах программирования. Далее мы будем работать именно с двоичными деревьями.
Кроме двоичных, широкое практическое применение имеют деревья с четырьмя узлами (дерево квадрантов). Они используются в геймдеве для организации сетки. Каждый узел в таком дереве представляет одно направление (север-запад, юго-восток и так далее).
Основные операции
Деревья – довольно сложные структуры. Для работы с иерархическими данными они должны предоставлять ряд алгоритмов.
Основные операции, которые нам нужны:
- Добавление нового узла (
add); - Удаление узла по его значению (
remove); - Поиск узла по значению (
find); - Обход всех элементов (
traverse).
При необходимости этот список можно расширить более сложными алгоритмами:
- Вставка/удаление поддерева;
- Вставка/удаление ветви;
- Вставка элемента в определенную позицию;
- Поиск наименьшего общего предка для двух узлов.
В этой статье мы рассмотрим только основные алгоритмы работы с деревьями, а более продвинутые вы сможете реализовать сами на их основе.
Мы реализуем дерево, начиная с корневого узла. Каждый узел будет содержать собственное значение, а также ссылки на дочерние элементы (на левый и на правый) и на родителя. Это очень похоже на связный список, который мы разбирали в прошлой статье.
При этом важно, чтобы не было дубликатов и у каждого узла был только один родитель.
class BinaryTreeNode {
constructor(value) {
this.left = null;
this.right = null;
this.parent = parent;
this.value = value;
}
get height() {
let leftHeight = this.left ? this.left.height + 1 : 0;
let rightHeight = this.right ? this.right.height + 1 : 0;
return Math.max(leftHeight, rightHeight);
}
}
let tree = new BinaryTreeNode('a');
Высота узла (height) вычисляется рекурсивно, на основе высоты его дочерних узлов.
Добавление узлов
Первый алгоритм, который мы должны реализовать для дерева, – это вставка новых узлов. Самая простая реализация не предъявляет никаких правил к расположению элементов, поэтому мы можем просто приписать новый узел к существующему как дочерний (с нужной стороны).
class BinaryTreeNode {
// …
setLeft(node) {
if (this.left) {
this.left.parent = null;
}
if (node) {
this.left = node;
this.left.parent = this;
}
}
setRight(node) {
if (this.right) {
this.right.parent = null;
}
if (node) {
this.right = node;
this.right.parent = this;
}
}
}
При вставке важно обновить все затронутые ссылки: left или right для родительского узла и parent для дочернего. Если у родителя уже был потомок, его свойство parent нужно обнулить.
Создание дерева
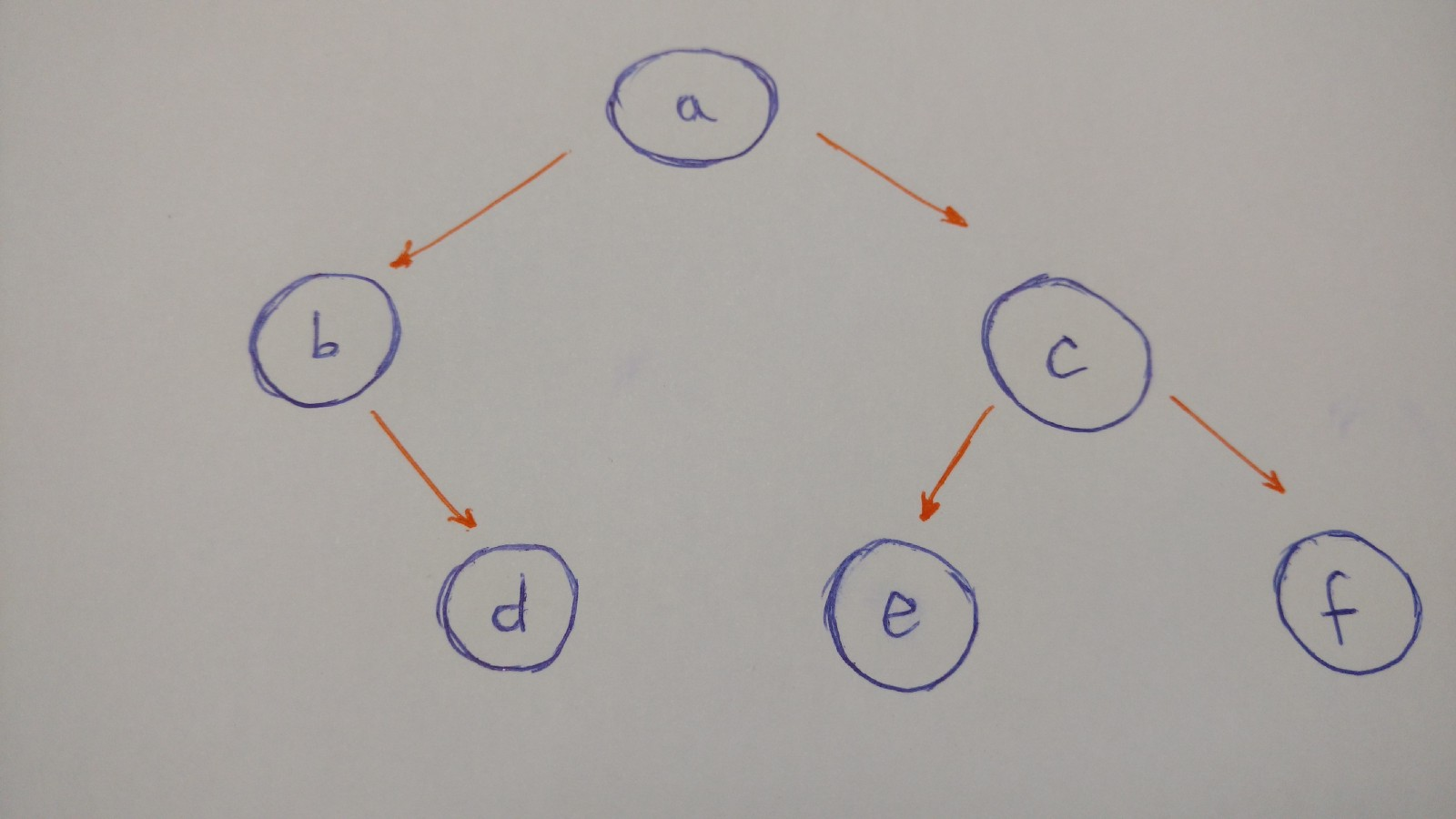
Реализация очень простая, но с ее помощью мы уже можем построить настоящее двоичное дерево, например, такое как на картинке:
let aNode = new BinaryTreeNode('a');
let bNode = new BinaryTreeNode('b');
aNode.setLeft(bNode);
let cNode = new BinaryTreeNode('c');
aNode.setRight(cNode);
let dNode = new BinaryTreeNode('d');
bNode.setRight(dNode);
let eNode = new BinaryTreeNode('e');
cNode.setLeft(eNode);
let fNode = new BinaryTreeNode('f');
cNode.setRight(fNode);
Обход дерева
Теперь нам нужен способ обойти все узлы дерева, чтобы выполнить для каждого из них какую-либо операцию.
Мы разберем два популярных алгоритма обхода дерева:
- поиск в глубину (depth-first search);
- поиск в ширину (breadth-first search).
DFS: Поиск в глубину
Идея обхода в глубину заключается в максимально возможном спуске по ветвям дерева вниз.
Алгоритм начинает с корневого узла и последовательно проверяет все исходящие из него ребра. Если ребро ведет в вершину, которая ранее не рассматривалась, то алгоритм рекурсивно запускается уже для нее, а после его выполнения продолжается проверка других ребер. Таким образом последовательно осматривается каждая ветка дерева.
function traverseDFRecursive(node, callback) {
// выполнение коллбэка для самого узла
callback(node);
// выполнение коллбэка для левого потомка
if (node.left) {
traverseDFRecursive(node.left, callback);
}
// выполнение коллбэка для правого потомка
if (node.right) {
traverseDFRecursive(node.right, callback);
}
}
function traverseDF(root, callback) {
traverseDFRecursive(root, callback);
}
Запустим перебор для нашего бинарного дерева:
traverseDF(aNode, node => console.log(node.value));
В консоли мы увидим следующее:
Существует три модификации алгоритма с разным способом перебора узлов:
- обход в прямом порядке, или предупорядоченный обход (pre-order walk). Перебор начинается с родительского узла и идет вниз, к дочерним.
- обход в обратном порядке, или поступорядоченный (post-order walk). Сначала перебираем левого и правого потомков, а потом родителя.
- симметричный обход. Начинаем с левого потомка, потом родитель, потом правый потомок.
Мы реализовали обход в прямом порядке, но можно использовать и другие способы.
BFS: Поиск в ширину
Алгоритм начинает с корневого узла (первый уровень) и двигается по всем ребрам, выходящим из него, перебирая последовательно каждый дочерний элемент (второй уровень). Когда все ребра проверены, алгоритм переходит на следующий уровень и начинает перебирать дочерние элементы дочерних элементов (элементы третьего уровня) и так далее.
Для реализации алгоритма обхода дерева в ширину мы будем использовать структуру данных очередь, которую уже разбирали в предыдущей статье цикла. На каждом шаге извлекаем из нее элемент, который был добавлен первым и перебираем всех его потомков. Каждый потомок также добавляется в очередь.
Можно использовать реализацию очереди из предыдущей статьи или воспользоваться простой очередью на базе JavaScript-массива.
class Queue {
constructor() {
this.arr = [];
}
enqueue(value) {
this.arr.push(value);
}
dequeue() {
return this.arr.shift();
}
isEmpty() {
return this.arr.length == 0;
}
}
function traverseBF(root, callback) {
let nodeQueue = new Queue();
nodeQueue.enqueue(root);
while(!nodeQueue.isEmpty()) {
let currentNode = nodeQueue.dequeue();
// Вызываем коллбэк для самого узла
callback(currentNode);
// Добавляем в очередь левого потомка
if (currentNode.left) {
nodeQueue.enqueue(currentNode.left);
}
// Добавляем в очередь правого потомка
if (currentNode.right) {
nodeQueue.enqueue(currentNode.right);
}
}
}
Запустим перебор в ширину:
traverseBF(aNode, node => console.log(node.value));
Результат выглядит так:
Бинарное дерево поиска
Одно из самых распространенных использований деревьев – упрощение поиска информации. В первой статье цикла мы говорили о том, что данные проще и быстрее искать в отсортированном массиве. Так вот, их также просто искать в упорядоченном дереве, о котором мы сейчас и поговорим.
Двоичное (бинарное) дерево поиска (binary search tree, BST) – это дерево, в котором элементы размещаются согласно определенному правилу (упорядоченно):
- Каждый узел должен быть «больше» любого элемента в своем левом поддереве.
- Каждый узел должен быть «меньше» любого элемента в своем правом поддереве.
Слова «больше» и «меньше» соответственно означают результат сравнения двух узлов функцией-компаратором.
Благодаря такой сортировке мы можем использовать все преимущества стратегии «разделяй и властвуй» – при поиске элемента можно смело отбрасывать половину дерева. Такие алгоритмы работают гораздо быстрее, чем линейный перебор каждого узла.
Важно:
Наша реализация предполагает отсутствие в дереве дублей (узлов с одинаковым значением). При необходимости их можно добавить, определив в каком поддереве они должны находиться.
Реализация на JavaScript
Для создания бинарного дерева поиска мы используем уже готовый класс BinaryTreeNode, немного его расширив. Необходимо добавить метод insert, определяющий логику вставки нового узла для сохранения сортировки. Также создадим отдельный класс для самого дерева, который будет хранить ссылку на корневой элемент и делегировать ему рекурсивное выполнение различных методов.
Так как бинарное дерево поиска является упорядоченным, нам еще потребуется функция-компаратор для сравнения элементов.
class BinarySearchTreeNode extends BinaryTreeNode {
constructor(value, comparator) {
super(value);
this.comparator = comparator;
}
insert(value) {
if (this.comparator(value, this.value) < 0) {
if (this.left) return this.left.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setLeft(newNode);
return newNode;
}
if (this.comparator(value, this.value) > 0) {
if (this.right) return this.right.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setRight(newNode);
return newNode;
}
return this;
}
}
class BinarySearchTree {
constructor(value, comparator) {
this.root = new BinarySearchTreeNode(value, comparator);
this.comparator = comparator;
}
insert(value) {
this.root.insert(value);
}
}
Метод insert, сравнивает значение нового элемента со значением узла и определяет, в какое поддерево его нужно поместить.
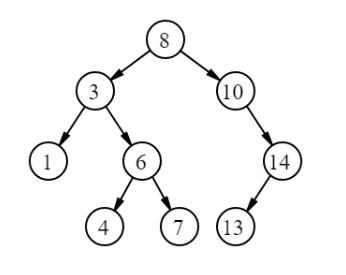
Создадим дерево как на картинке выше:
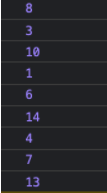
const tree = new BinarySearchTree(8, (a, b) => a - b);
tree.insert(3);
tree.insert(10);
tree.insert(14);
tree.insert(1);
tree.insert(6);
tree.insert(4);
tree.insert(7);
tree.insert(13);
А теперь обойдем все его элементы, чтобы убедиться, что оно сформировано правильно:
traverseBF(tree.root);
Поиск в бинарном дереве поиска
Все эти сложности со вставкой новых узлов и сортировкой дерева нужны для того, чтобы обеспечить удобный поиск по нему.
Алгоритм поиска в BST очень похож на двоичный поиск в отсортированном массиве, который мы разбирали в первой части цикла. Сравниваем искомое значение с корневым узлом, определяем, в каком поддереве нужно искать, а второе поддерево просто отбрасываем.
class BinarySearchTree {
find(value) {
return this.root.find(value);
}
}
class BinarySearchTreeNode {
find(value) {
if (this.comparator(this.value, value) === 0) return this;
if (this.comparator(this.value, value) < 0 && this.left) {
return this.left.find(value);
}
if (this.comparator(this.value, value) > 0 && this.right) {
return this.right.find(value);
}
return null;
}
}
Алгоритм поиска рекурсивно проверяет все узлы, пока не найдет подходящий.
Удаление узлов
Удаление узлов из BST – это достаточно сложный алгоритм, так как после удаления узла необходимо восстановить структуру дерева, чтобы оно оставалось отсортированным.
Есть три сценария:
- У удаляемого узла нет потомков (листовой узел).
- У удаляемого узла один потомок (левый или правый).
- У удаляемого узла два потомка.
- Первый случай самый простой и не требует перестройки дерева после удаления.
- Во втором случае после удаления нужно установить связь между родителем удаленного узла и его потомком. Все потомки удаленного узла в любом случае находятся с той же стороны от его родителя, что и сам узел. Поэтому мы записываем их с той же стороны, на которой находился удаленный узел.
- Третий случай самый сложный. Мы должны найти следующий по порядку узел (минимальный узел в правом поддереве удаляемого узла) и поставить его вместо удаляемого.
Для реализации алгоритма удаления нам понадобится несколько вспомогательных методов.
class BinarySearchTreeNode {
// ...
findMin() {
if (!this.left) {
return this;
}
return this.left.findMin();
}
removeChild(nodeToRemove) {
if (this.left && this.left === nodeToRemove) {
this.left = null;
return true;
}
if (this.right && this.right === nodeToRemove) {
this.right = null;
return true;
}
return false;
}
replaceChild(nodeToReplace, replacementNode) {
if (!nodeToReplace || !replacementNode) {
return false;
}
if (this.left && this.left === nodeToReplace) {
this.left = replacementNode;
return true;
}
if (this.right && this.right === nodeToReplace) {
this.right = replacementNode;
return true;
}
return false;
}
}
findMinищет минимальный элемент в поддереве.removeChildудаляет указанный элемент, если он является дочерним для данного узла.replaceChildзаменяет дочерний элемент на новый.
Теперь добавим в класс BinarySearchTree новый метод remove:
class BinarySearchTree {
//...
insert(value) {
if (!this.root.value) this.root.value = value;
else this.root.insert(value);
}
remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) {
throw new Error('Item not found');
}
const parent = nodeToRemove.parent;
// Нет потомков, листовой узел
if (!nodeToRemove.left && !nodeToRemove.right) {
if (parent) {
// Удалить у родителя указатель на удаленного потомка
parent.removeChild(nodeToRemove);
} else {
// Нет родителя, корневой узел
nodeToRemove.value = undefined;
}
}
// Есть и левый, и правый потомки
else if (nodeToRemove.left && nodeToRemove.right) {
// Ищем минимальное значение в правом поддереве
// И ставим его на место удаляемого узла
const nextBiggerNode = nodeToRemove.right.findMin();
if (this.comparator(nextBiggerNode, nodeToRemove.right) === 0) {
// Правый потомок одновременно является минимальным в правом дереве
// то есть у него нет левого поддерева
// можно просто заменить удаляемый узел на его правого потомка
nodeToRemove.value = nodeToRemove.right.value;
nodeToRemove.setRight(nodeToRemove.right.right);
} else {
// Удалить найденный узел (рекурсия)
this.remove(nextBiggerNode.value);
// Обновить значение удаляемого узла
nodeToRemove.value = nextBiggerNode.value;
}
}
// Есть только один потомок (левый или правый)
else {
// Заменить удаляемый узел на его потомка
const childNode = nodeToRemove.left || nodeToRemove.right;
if (parent) {
parent.replaceChild(nodeToRemove, childNode);
} else {
this.root = childNode;
}
}
// Удалить ссылку на родителя
nodeToRemove.parent = null;
return true;
}
}
Обратите внимание, в результате удаления возможна ситуация, в которой дерево остается пустым (удаляется корневой элемент, не имеющий потомков). В этом случае мы просто удаляем значение элемента root. Из-за этого требуется небольшая доработка метода insert: если у корневого элемента нет значения, мы просто присваиваем ему новое.
Полный код
Полная реализация бинарного дерева поиска на JavaScript:
class BinarySearchTreeNode extends BinaryTreeNode {
constructor(value, comparator) {
super(value);
this.comparator = comparator;
}
insert(value) {
if (this.comparator(value, this.value) < 0) {
if (this.left) return this.left.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setLeft(newNode);
return newNode;
}
if (this.comparator(value, this.value) > 0) {
if (this.right) return this.right.insert(value);
let newNode = new BinarySearchTreeNode(value, this.comparator);
this.setRight(newNode);
return newNode;
}
return this;
}
find(value) {
if (this.comparator(this.value, value) === 0) return this;
if (this.comparator(this.value, value) < 0 && this.left) {
return this.left.find(value);
}
if (this.comparator(this.value, value) > 0 && this.right) {
return this.right.find(value);
}
return null;
}
findMin() {
if (!this.left) {
return this;
}
return this.left.findMin();
}
removeChild(nodeToRemove) {
if (this.left && this.left === nodeToRemove) {
this.left = null;
return true;
}
if (this.right && this.right === nodeToRemove) {
this.right = null;
return true;
}
return false;
}
replaceChild(nodeToReplace, replacementNode) {
if (!nodeToReplace || !replacementNode) {
return false;
}
if (this.left && this.left === nodeToReplace) {
this.left = replacementNode;
return true;
}
if (this.right && this.right === nodeToReplace) {
this.right = replacementNode;
return true;
}
return false;
}
}
class BinarySearchTree {
constructor(value, comparator) {
this.root = new BinarySearchTreeNode(value, comparator);
this.comparator = comparator;
}
insert(value) {
if (!this.root.value) this.root.value = value;
else this.root.insert(value);
}
find(value) {
return this.root.find(value);
}
remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) {
throw new Error('Item not found');
}
const parent = nodeToRemove.parent;
// Нет потомков, листовой узел
if (!nodeToRemove.left && !nodeToRemove.right) {
if (parent) {
// Удалить у родителя указатель на удаленного потомка
parent.removeChild(nodeToRemove);
} else {
// Нет родителя, корневой узел
nodeToRemove.value = undefined;
}
}
// Есть и левый, и правый потомки
else if (nodeToRemove.left && nodeToRemove.right) {
// Ищем минимальное значение в правом поддереве
// И ставим его на место удаляемого узла
const nextBiggerNode = nodeToRemove.right.findMin();
if (this.comparator(nextBiggerNode, nodeToRemove.right) === 0) {
// Правый потомок одновременно является минимальным в правом дереве
// то есть у него нет левого поддерева
// можно просто заменить удаляемый узел на его правого потомка
nodeToRemove.value = nodeToRemove.right.value;
nodeToRemove.setRight(nodeToRemove.right.right);
} else {
// Удалить найденный узел (рекурсия)
this.remove(nextBiggerNode.value);
// Обновить значение удаляемого узла
nodeToRemove.value = nextBiggerNode.value;
}
}
// Есть только один потомок (левый или правый)
else {
// Заменить удаляемый узел на его потомка
const childNode = nodeToRemove.left || nodeToRemove.right;
if (parent) {
parent.replaceChild(nodeToRemove, childNode);
} else {
this.root = childNode;
}
}
// Удалить ссылку на родителя
nodeToRemove.parent = null;
return true;
}
}
Эффективность
Временная сложность всех основных операций в бинарном дереве составляет log(n) – это довольно эффективная структура данных.
| Индексация | Поиск | Вставка | Удаление |
| O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
Сбалансированные бинарные деревья
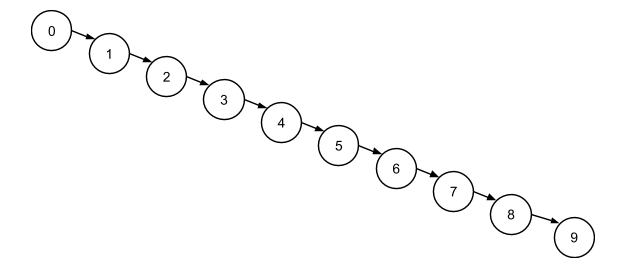
Несмотря на строгие правила сортировки элементов бинарное дерево поиска может оказаться крайне неэффективным.
На картинке изображено валидное бинарное дерево поиска. Для каждого узла соблюдается правило: все узлы в правом поддереве имеют большее значение. Однако такое дерево не позволяет нам пользоваться преимуществами стратегии «разделяй и властвуй», ведь тут нечего отбрасывать. Говорят, что дерево выродилось в список.
Чтобы избежать таких ситуаций, используются более сложные структуры данных – самобалансирующиеся деревья:
- AVL-дерево
- Красно-черное дерево
Эти деревья используют различные алгоритмы «выравнивания» при вставке и удалении элементов.
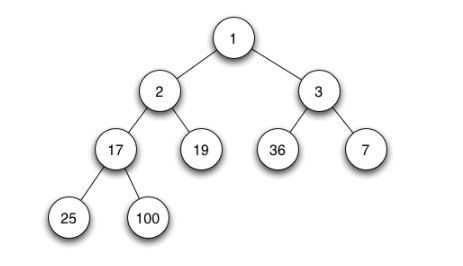
Легким движением руки несбалансированное дерево поиска превращается в сбалансированное:
Визуализация самобалансирующихся деревьев:
- AVL-дерево
- Красно-черное дерево
Двоичная куча
Еще одна древоподобная структура, о которой следует знать – это куча.
У кучи также есть корень, а элементы могут иметь дочерние узлы. У двоичной кучи каждый узел может иметь не более двух потомков.
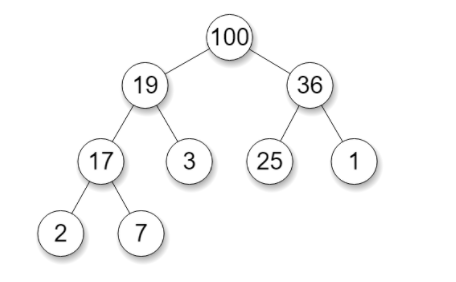
Как и бинарное дерево поиска, куча имеет определенные требования к размещению элементов: все потомки узла должны быть меньше его. Куча, соответствующая этому правилу, называется max-кучей. В ней корень всегда является максимальным элементом.
Бывают также min-кучи, которые следуют противоположному правилу: все потомки узла должны быть больше его. Таким образом, корнем всегда оказывается минимальный элемент кучи.
Куча – это самобалансирующаяся структура, при каждой операции она сортирует себя, чтобы все уровни дерева (кроме последнего) были заполнены.
По сути, куча – это очередь с приоритетом. Каждый новый элемент размещается в этой очереди в соответствии с его приоритетом, чем приоритет выше, тем ближе он к началу очереди.
Каждую кучу можно представить в виде линейного массива:
Чаще всего используется именно линейная реализация, однако дерево более наглядно демонстрирует принцип распределения.
Основные операции
Базовые операции с кучей такие же, как и с очередью:
- найти элемент с максимальным приоритетом (максимальный элемент в max-куче или минимальный элемент в min-куче);
- удалить элемент с максимальным приоритетом;
- добавить в очередь новый элемент.
Реализация
Мы реализуем на JavaScript min-кучу. Для max-кучи нужно только изменить операцию сравнения.
class Heap {
constructor(comparator) {
this.arr = [];
this.comparator = comparator;
}
isCorrectOrder(first, second) {
return this.comparator(first, second) < 0;
}
}
Так как элементы кучи хранятся в виде массива по уровням, нужно определить вспомогательные методы для нахождения потомков и родителей конкретного узла. Мы можем это сделать, так как куча является полным деревом, то есть не имеет пропусков в своей структуре. Индекс нужного элемента в массиве можно вычислить, исходя из его позиции в дереве.
class Heap {
// ...
getLeftChildIndex(parentIndex) {
return (2 * parentIndex) + 1;
}
getRightChildIndex(parentIndex) {
return (2 * parentIndex) + 2;
}
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2);
}
leftChild(parentIndex) {
return this.arr[this.getLeftChildIndex(parentIndex)];
}
rightChild(parentIndex) {
return this.arr[this.getRightChildIndex(parentIndex)];
}
parent(childIndex) {
return this.arr[this.getParentIndex(childIndex)];
}
}
Добавим еще несколько вспомогательных методов для удобных проверок:
class Heap {
// ...
hasParent(childIndex) {
return this.getParentIndex(childIndex) >= 0;
}
hasLeftChild(parentIndex) {
return this.getLeftChildIndex(parentIndex) < this.arr.length;
}
hasRightChild(parentIndex) {
return this.getRightChildIndex(parentIndex) < this.arr.length;
}
isEmpty() {
return !this.arr.length;
}
}
Добавление элемента
Сначала новый элемент помещается в самый конец кучи (конец массива), как и в обычной очереди, а затем начинается процесс его поднятия вверх с учетом приоритета. Это рекурсивный алгоритм, который сравнивает элемент с предыдущим и при необходимости меняет их местами.
class Heap {
// ...
push(item) {
this.arr.push(item);
this.heapifyUp();
return this;
}
heapifyUp(startIndex) {
let currentIndex = startIndex || this.arr.length - 1;
while (
this.hasParent(currentIndex)
&& !this.isCorrectOrder(this.parent(currentIndex), this.arr[currentIndex])
) {
let parentIndex = this.getParentIndex(currentIndex);
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
}
}
swap(indexOne, indexTwo) {
const tmp = this.arr[indexTwo];
this.arr[indexTwo] = this.arr[indexOne];
this.arr[indexOne] = tmp;
}
}
Получение элемента с максимальным приоритетом
Для получения элемента с начала очереди может быть два метода:
peek– просмотр без удаления;pop– получение элемента и удаление его из очереди.
С peek все понятно, нам просто нужно взять нулевой элемент массива. А вот после удаления необходимо перебалансировать дерево. Для этого мы берем самый последний элемент массива, ставим его в начало и начинаем сдвигать вниз, последовательно сравнивая с его дочерними элементами.
class Heap {
// ...
peek() {
if (this.arr.length === 0) {
return null;
}
return this.arr[0];
}
pop() {
if (this.arr.length === 0) {
return null;
}
if (this.arr.length === 1) {
return this.arr.pop();
}
const item = this.arr[0];
this.arr[0] = this.arr.pop();
this.heapifyDown();
return item;
}
heapifyDown(customStartIndex = 0) {
let currentIndex = customStartIndex;
let nextIndex = null;
while (this.hasLeftChild(currentIndex)) {
if (
this.hasRightChild(currentIndex)
&& this.isCorrectOrder(this.rightChild(currentIndex), this.leftChild(currentIndex))
) {
nextIndex = this.getRightChildIndex(currentIndex);
} else {
nextIndex = this.getLeftChildIndex(currentIndex);
}
if (this.isCorrectOrder(
this.arr[currentIndex],
this.arr[nextIndex],
)) {
break;
}
this.swap(currentIndex, nextIndex);
currentIndex = nextIndex;
}
}
}
Полный код
class Heap {
constructor(comparator) {
this.arr = [];
this.comparator = comparator;
}
isCorrectOrder(first, second) {
return this.comparator(first, second) < 0;
}
getLeftChildIndex(parentIndex) {
return (2 * parentIndex) + 1;
}
getRightChildIndex(parentIndex) {
return (2 * parentIndex) + 2;
}
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2);
}
leftChild(parentIndex) {
return this.arr[this.getLeftChildIndex(parentIndex)];
}
rightChild(parentIndex) {
return this.arr[this.getRightChildIndex(parentIndex)];
}
parent(childIndex) {
return this.arr[this.getParentIndex(childIndex)];
}
hasParent(childIndex) {
return this.getParentIndex(childIndex) >= 0;
}
hasLeftChild(parentIndex) {
return this.getLeftChildIndex(parentIndex) < this.arr.length;
}
hasRightChild(parentIndex) {
return this.getRightChildIndex(parentIndex) < this.arr.length;
}
isEmpty() {
return !this.arr.length;
}
swap(indexOne, indexTwo) {
const tmp = this.arr[indexTwo];
this.arr[indexTwo] = this.arr[indexOne];
this.arr[indexOne] = tmp;
}
push(item) {
this.arr.push(item);
this.heapifyUp();
return this;
}
heapifyUp(startIndex) {
let currentIndex = startIndex || this.arr.length - 1;
while (
this.hasParent(currentIndex)
&& !this.isCorrectOrder(this.parent(currentIndex), this.arr[currentIndex])
) {
let parentIndex = this.getParentIndex(currentIndex);
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
}
}
peek() {
if (this.arr.length === 0) {
return null;
}
return this.arr[0];
}
pop() {
if (this.arr.length === 0) {
return null;
}
if (this.arr.length === 1) {
return this.arr.pop();
}
const item = this.arr[0];
this.arr[0] = this.arr.pop();
this.heapifyDown();
return item;
}
heapifyDown(customStartIndex = 0) {
let currentIndex = customStartIndex;
let nextIndex = null;
while (this.hasLeftChild(currentIndex)) {
if (
this.hasRightChild(currentIndex)
&& this.isCorrectOrder(this.rightChild(currentIndex), this.leftChild(currentIndex))
) {
nextIndex = this.getRightChildIndex(currentIndex);
} else {
nextIndex = this.getLeftChildIndex(currentIndex);
}
if (this.isCorrectOrder(
this.arr[currentIndex],
this.arr[nextIndex],
)) {
break;
}
this.swap(currentIndex, nextIndex);
currentIndex = nextIndex;
}
}
}
- Прекрасная визуализация работы кучи.
Заключение
Деревья – довольно сложная (по сравнению с линейными), но очень интересная структура данных. Об одном из самых популярных ее применений (поиске данных) мы уже поговорили.
Деревья также широко применяются для управления различными иерархиями (каталоги), принятием решений (игры), а также для парсинга и синтаксического разбора выражений. Различные компиляторы основаны именно на деревьях. Значение деревьев в программирование очень велико, так как они позволяют вырваться из линейных структур и обеспечить более удобный в ряде случаев способ представления данных.
В следующей статье мы пойдем еще дальше и поговорим самой нелинейной структуре – графах – и алгоритмах работы с ней.
***
Больше полезной информации вы найдете на наших телеграм-каналах «Библиотека программиста» и «Книги для программистов».