Как найти уровень жидкости в конусе - Исправление недочетов и поиск решений вместе с Examum.ru

Всего: 21 1–20 | 21–21

Добавить в вариант

В цилиндрический сосуд налили 2000 см³ воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см³.

В цилиндрический сосуд налили 1200 см³ воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ выразите в см³.

В цилиндрическом сосуде уровень жидкости достигает 8 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в сантиметрах.

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.

В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.

В цилиндрический сосуд налили 5000 см³ воды. Уровень воды при этом достигает высоты 14 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 7 см. Чему равен объем детали? Ответ выразите в

В цилиндрический сосуд налили 1000 см³ воды. Уровень воды при этом достигает высоты 20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 4 см. Чему равен объем детали? Ответ выразите в см³.

В цилиндрическом сосуде уровень жидкости достигает 180 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 6 раз больше первого? Ответ выразите в сантиметрах.

В цилиндрическом сосуде уровень жидкости достигает 128 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 8 раз больше первого? Ответ выразите в сантиметрах.

В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,9 раза. Чему равен объем детали? Ответ выразите в литрах.

В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 54 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

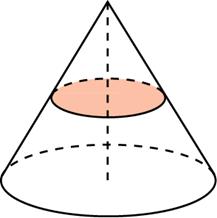
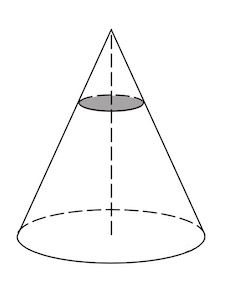
В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.). Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?

В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 14 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?

В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 40 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху?

В цилиндрический сосуд налили 600 см³ воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,6 раза. Найдите объем детали. Ответ выразите в см³.

В цилиндрический сосуд налили 2200 см³ воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 6 см. Чему равен объём детали? Ответ выразите в см³.

В цилиндрический сосуд налили 1800 см³ воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 2 см. Чему равен объём детали? Ответ выразите в см³.

В цилиндрическом сосуде уровень жидкости достигает 147 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ дайте в сантиметрах.

Всего: 21 1–20 | 21–21

Источник

Формулировка задачи: В сосуде, имеющем форму конуса, уровень жидкости достигает K/L высоты. Объём сосуда N мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).

Рассмотрим, как решаются подобные задачи на примерах и выведем общий способ решения.

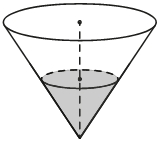
Пример задачи 1:

В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.

Решение:

Судя по картинке, есть 2 конуса: большой и малый, полностью заполненный водой. Данные конусы подобны с коэффициентом подобия, равным 1/2, так как большой конус заполнен водой ровно наполовину.

Поскольку в задаче дан объем большего конуса и по нему нужно получить объем меньшего, а объемы любых двух подобных объемных фигур относятся как куб коэффициента подобия, можно составить следующее соотношение:

V_{мал.кон.} / V_{бол.кон.} = (1/2)³

Выразим из этого соотношения объем малого конуса и вычислим его:

V_{мал.кон.} = V_{бол.кон.} ⋅ (1/2)³ = 1600 / 8 = 200 мл

Ответ: 200

Пример задачи 2:

В сосуде, имеющий форму конуса, уровень жидкости достигает 6/7 высоты. Объем сосуда 3430 мл. Чему равен объём налитой жидкости? Ответ дайте в миллиметрах.

Решение:

В задаче присутствуют 2 подобных конуса. Поскольку высота меньшего конуса составляет 6/7 высоты большего, это число является коэффициентом подобия. Объемы любых двух подобных объемных фигур относятся как куб коэффициента подобия, поэтому можно составить следующее соотношение:

V_{мал.кон.} / V_{бол.кон.} = (6/7)³

Выразим из этого соотношения объем малого конуса и вычислим его:

V_{мал.кон.} = V_{бол.кон.} ⋅ (6/7)³ = 3430 ⋅ 216 / 343 = 2160 мл

Ответ: 2160

В общем виде решение данной задачи по стереометрии выглядит следующим образом:

ОБЪЕМ ЖИДКОСТИ = N ⋅ (K/L)³

где N – объем сосуда, K/L – часть высоты, которую занимает уровень жидкости.

Остается лишь подставить конкретные значения и подсчитать результат.

Источник

План изучения темы

Понятие конуса.
Площадь поверхности конуса.
Объём конуса.
Усечённый конус.
Площадь поверхности усечённого конуса.
Объём усечённого конуса.
Решение задач на тему «Конус».

Понятие конуса

Конус — геометрическое тело, образованное конической поверхностью и пересекающей её плоскости, не проходящей через точку Р (рисунок выше). Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета. На рисунке ниже треугольник РОА вращают вокруг катета РО.

Точка Р — вершина конуса. РО — ось конуса, а её отрезок, заключенный между вершиной и основанием — высота конуса. Основание конуса — это круг, на который опирается данная геометрическая фигура. Любая прямая, соединяющая вершину Р с точкой на окружности основания (РА, РВ) — это образующая конуса (обозначается l). Поверхность, составленная их образующих — это боковая поверхность конуса.

Площадь поверхности конуса

Как и цилиндр, конус имеет два вида площадей — площадь боковой поверхности и площадь полной поверхности.

Развёртка конуса представляет собой сектор. Отсюда есть разные формулы нахождения площади боковой поверхности.

Это формула при использовании развёртки, как сектора. Если же учесть, что длина дуги сектора равна длине окружности основания конуса, то получаем равенство:

где r — радиус основания конуса. Тогда имеем вторую, более простую формулу нахождения площади боковой поверхности конуса:

Площадь полной поверхности состоит из боковой и основания конуса. Значит, формула нахождения этой площади:

Объём конуса

где r — радиус основания конуса, h — высота конуса.

Усечённый конус

Если на какой-либо высоте конуса провести секущую плоскость, параллельную основанию, то мы получим две фигуры: конус меньшего объёма сверху и усечённый конус внизу. При этом, составляющие элементы будут как у обычного конуса: образующие, ось, высота, боковая поверхность. Отличие — будет уже два основания, которые отличаются по площади.

Площадь поверхности усечённого конуса

Из-за того, что теперь у нас два основания, формула площади боковой поверхности усеченного конуса будет выглядеть иначе:

Само собой, меняется и формула площади полной поверхности:

Объём усечённого конуса

Решение задач на тему «Конус»

Пример 1 (Ященко 36 вариантов, 2021 год, вариант 7)

В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 высоты. Объём жидкости составляет 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд.

Решение: объём конуса вычисляется по формуле:

Высота налитой жидкости 0,25 от всей высоты конуса. Значит, высота в 4 раза больше. Но при этом, не забывайте, что радиус всего конуса тоже увеличится в 4 раза. Так как мы на осевом сечении получаем случай подобных треугольников:

С учётом таких изменений, наш новый объём (объём всего конуса) примет вид:

Видим, что объём всего конуса в 64 раза больше налитой жидкости. Значит, в миллилитрах это будет:

Получается, что долить нужно 315 миллилитров.

Ответ: 315

Пример 2 (Ященко 36 вариантов, 2021 год, вариант 11)

Цилиндр и конус имеют общее основание и высоту. Объём цилиндра равен 162. Найдите объём конуса.

Решение: формулы объёмов цилиндра и конуса отличаются незначительно.

Видим, что отличие только в дроби 1/3 в формуле объёма конуса. А раз по условию высота и основания совпадают, значит объём конуса будет просто в 3 раза меньше. Значит, он равен 54.

Ответ: 54

Пример 3 (Ященко 36 вариантов, 2021 год, вариант 25)

Площадь боковой поверхности конуса равна 30. Параллельно основанию конуса проведено сечение, делящее его высоту в отношении 2:3, считая от вершины конуса. Найдите площадь боковой поверхности отсечённого конуса.

Решение: разберемся для начала, какие подобные треугольники тут можно получить.

Видим, что треугольник SAD подобен треугольнику SBC с коэффициентом подобия 2/5. Значит, площади боковых поверхностей конуса и отсечённого конуса будут иметь отношение подобия в квадрате (из-за того, что это площади, а не длины каких-то сторон).

Отсечённый конус — это тот, что сверху, маленький. Значит, с учётом коэффициента подобия:

Ответ: 4,8

Источник

В сосуде, имеющий форму конуса, уровень жидкости достигает 3/4 высоты. Объем сосуда равен 1680 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.

Решение:
Сосуд, имеет форму конуса.
Объём конуса находится по формуле:
V=1/3*πR² *h и данный сосуд согласно условия задачи вмещает 1680мл жидкости.
Если уровень жидкости достигает 3/4 высоты, то объём жидкости в сосуде выразим:
V=1/3*πR² *3/4*h -обозначим этот объём жидкости за (х) мл
Решим задачу методом пропорции:
1/3*πR² *h — 1680
1/3*πR² *3/4*h — х
х=1/3*πR² *3/4*h*1680/ 1/3*πR² *h=3/4*1680=5040/4=1260 (мл)

Ответ: Объём налитой жидкости в сосуде 1260мл

Если вы не нашли ответа на свой вопрос, или сомневаетесь в его правильности, то можете воспользоваться формой ниже и уточнить решение. Или воспользуйтесь формой поиска и найдите похожие ответы по предмету Алгебра.

Источник

09
Сен 2013

Категория: 02 Стереометрия

02. Конус

2013-09-09
2022-09-11

Задача 1. Высота конуса равна , образующая равна Найдите его объем, деленный на .

Решение: + показать

Задача 2. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного Найдите его объем, деленный на .

Решение: + показать

Задача 3. Высота конуса равна а диаметр основания – Найдите образующую конуса.

Решение: + показать

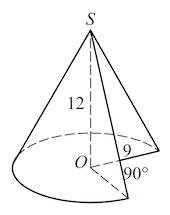
Задача 4. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом В ответе укажите $frac{V}{pi}.$

Решение: + показать

Задача 5. Длина окружности основания конуса равна образующая равна Найдите площадь боковой поверхности конуса.

Решение: + показать

Задача 6. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в раз?

Решение: + показать

Задача 7. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в раз?

Решение: + показать

Задача 8. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в раз, а высота останется прежней?

Решение: + показать

Задача 9. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Решение: + показать

Задача 10. Объем конуса равен Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решение: + показать

Задача 11. Площадь полной поверхности конуса равна Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Решение: + показать

Задача 12. Найдите объем конуса, образующая которого равна и наклонена к плоскости основания под углом $30^{circ}.$ В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 13. Диаметр основания конуса равен а угол при вершине осевого сечения равен °. Вычислите объем конуса, деленный на .

Решение: + показать

Задача 14. Площадь основания конуса равна , высота — Найдите площадь осевого сечения конуса.

Решение: + показать

Задача 15. Площадь основания конуса равна Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной и считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Решение: + показать

Задача 16. Найдите объем части конуса, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 17. Найдите объем части конуса, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 18. В сосуде, имеющем форму конуса, уровень жидкости достигает $frac{1}{2}$ высоты. Объём жидкости равен мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Решение: + показать

Вы можете пройти тест

Автор: egeMax |

комментариев 10

Печать страницы

Источник