Исходный полный конус
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
- Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
- Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
- Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.
Существующие виды
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
- Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
- Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
- Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.
Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
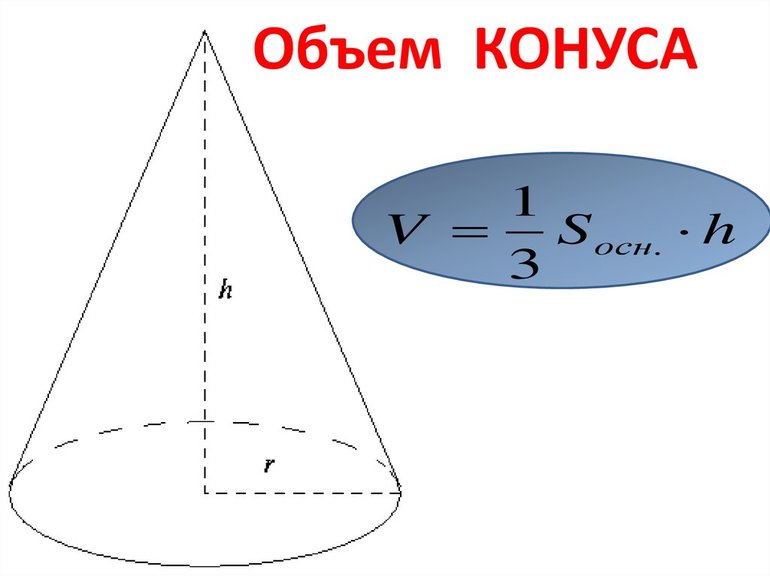
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r2*h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
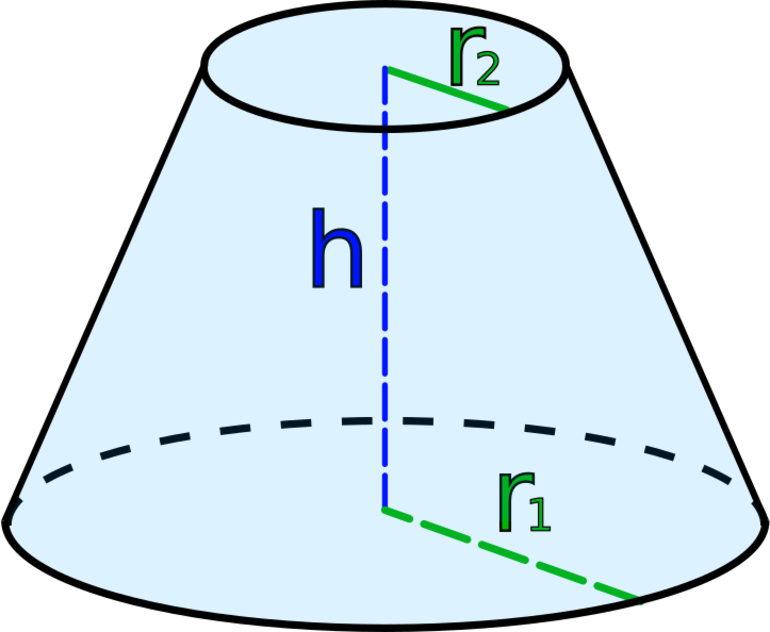
Усеченный геометрический объект
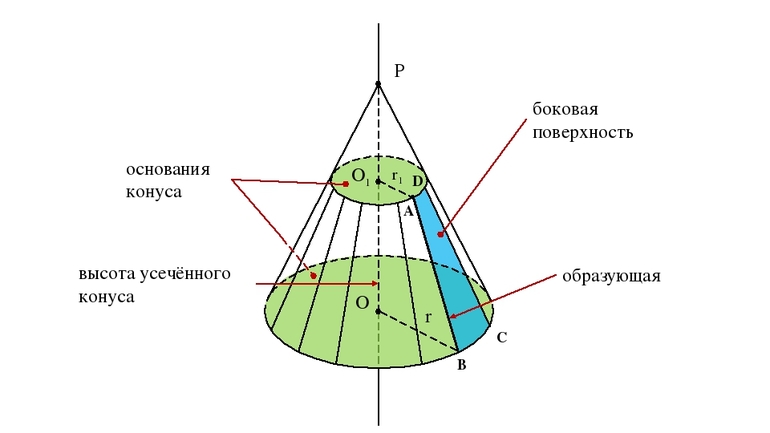
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
Площадь поверхности
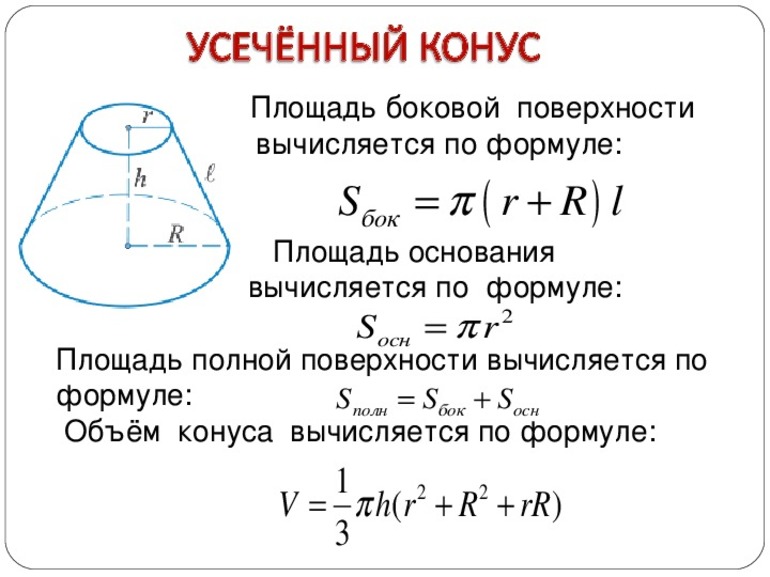
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:
- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r12 + r22 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
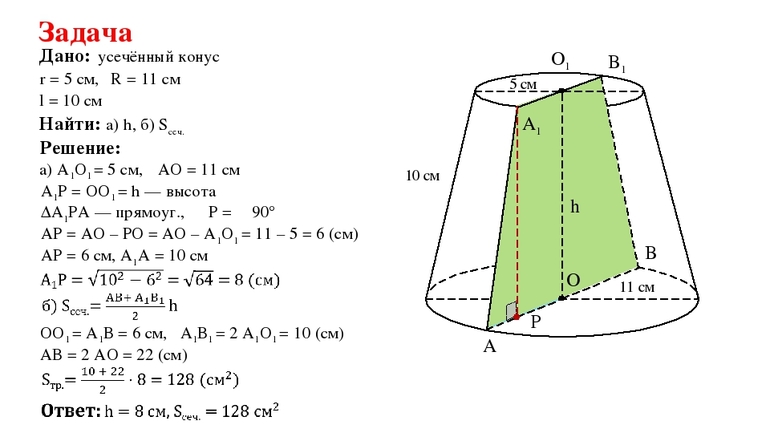
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см2. При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r12 + pi*r22 = 4*pi*r22 + pi*r22 = 5*pi*r22.
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h2)^0,5 = (2,522 + 152 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см2.
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.

Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r2*h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Усеченный геометрический объект
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r12 + r22 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см2. При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r12 + pi*r22 = 4*pi*r22 + pi*r22 = 5*pi*r22.
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.

Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h2)^0,5 = (2,522 + 152 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см2.
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
Источник
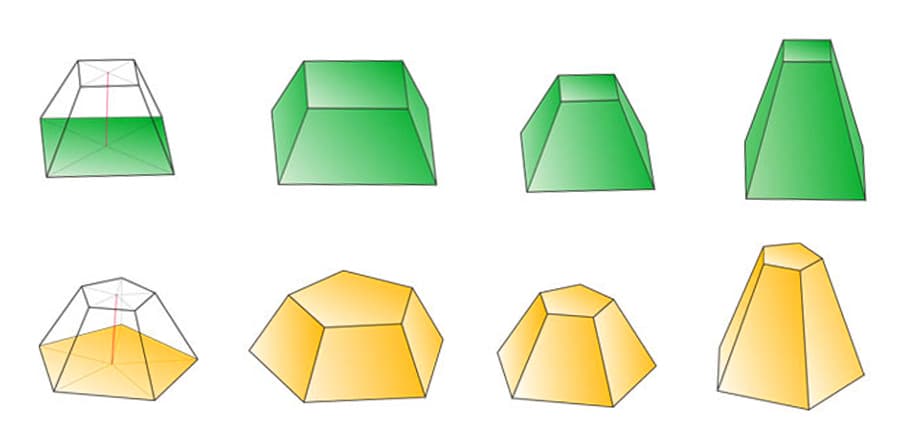
Что такое усеченная пирамида? Свойства и формулы. Пирамиды индейцев майя
Одним из симметричных полиэдров, свойства которого изучает стереометрия, является пирамида. В данной статье рассмотрим подробнее следующие вопросы: что такое пирамида усеченная, как ее можно получить и какими свойствами она характеризуется.
Полная пирамида
Прежде чем раскрывать вопрос, что такое пирамида усеченная, следует дать определение пирамиды в общем случае.
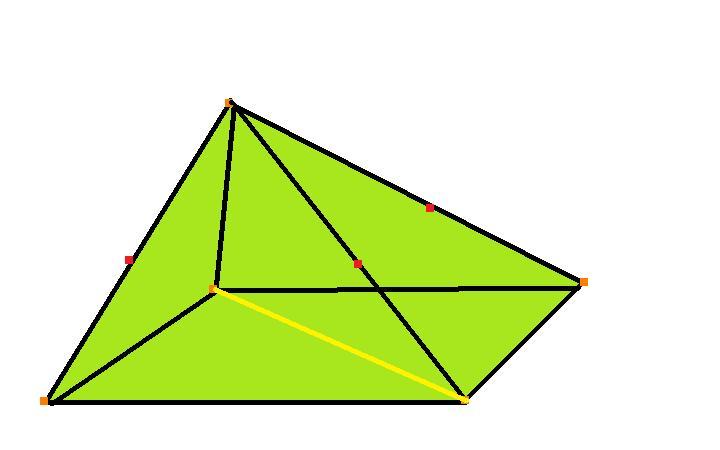
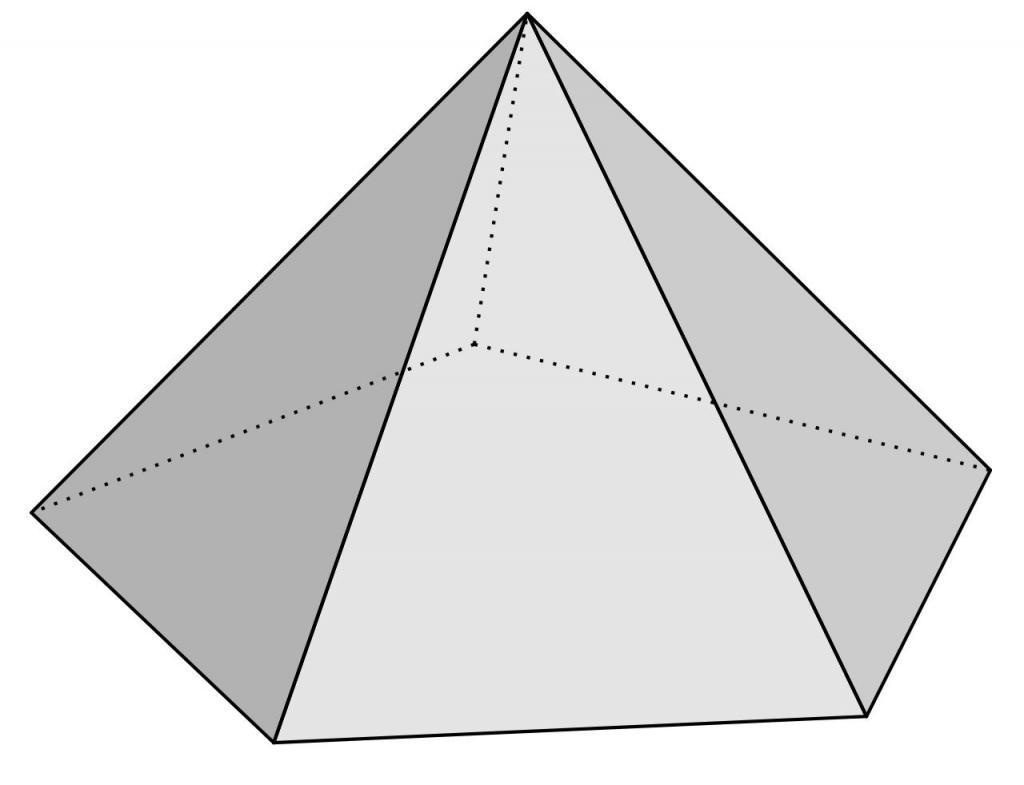
Под пирамидой в геометрии понимают фигуру в трехмерном пространстве, которая состоит из n треугольных граней и одной n-угольной стороны, которая называется основанием. Представить себе пирамиду достаточно просто: необходимо мысленно соединить все углы n-угольника с некоторой одной точкой в пространстве. Рисунок ниже показывает фигуру, которая при этом получается.
Здесь мы видим, что углы четырехугольного основания соединены отрезками с одной точкой, которая называется вершиной пирамиды. Боковая поверхность фигуры образована четырьмя разными треугольниками.
Если все треугольники боковой поверхности будут одинаковыми и равнобедренными, то такая фигура называется прямой пирамидой. Если к тому же основание будет представлять правильный n-угольник, например, квадрат, то говорят о пирамиде правильной.
Усеченная пирамида
Рассмотренная выше фигура называется полной пирамидой. Теперь покажем, что такое усеченная пирамида и как ее можно получить из полной.
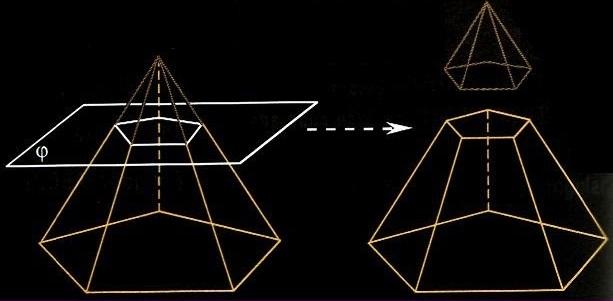
Пусть у нас имеется полная фигура с пятиугольным основанием. Она показана ниже на рисунке слева.
Возьмем произвольную плоскость и отсечем верхнюю часть у полной пирамиды. Плоскость разделит исходную фигуру на две части: верхняя будет представлять также пирамиду, а вот нижняя — это уже усеченная пирамида (см. правое изображение на рисунке).
Заметим, что в данном случае мы выбрали секущую плоскость, которая параллельна основанию исходной фигуры. Полученная из правильной фигуры с помощью параллельного сечения усеченная пирамида также будет называться правильной.
Рисунок также показывает, что основания усеченной пирамиды (пятиугольники в примере) образованы подобными правильными многоугольниками, при этом размер верхнего будет всегда меньше, чем нижнего. Боковая поверхность этой фигуры, в отличие от полной пирамиды, образована равнобедренными трапециями.
Если в основании усеченной пирамиды лежит n-угольник, тогда она имеет 2 × n вершин, 3 × n ребер и n + 2 стороны.
Двумя важными геометрическими параметрами рассматриваемой фигуры являются площадь ее поверхности и объем.
Поверхность пирамиды усеченной
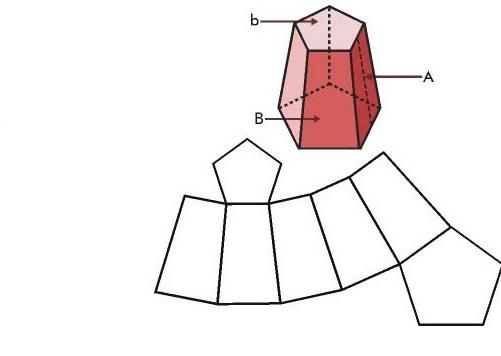
Рассмотрев, что такое усеченная пирамида, перейдем к изучению ее поверхности. Под последней понимают совокупность всех граней, образующих фигуру. Проще всего свойства поверхности изучать на примере развертки. Рисунок ниже показывает развертку для пирамиды с пятиугольными основаниями.
Чтобы вычислить площадь всей ее поверхности, необходимо сложить площадь двух оснований и площадь всех трапеций. Соответствующая формула имеет вид:
S = So1 + So2 + 1/2 × (Po1 + Po2) × Ap.
В этом выражении первые два члена, то есть So1 и So2, представляют собой площади оснований. Третий член — это суммарная площадь всех трапеций, которая равна половине произведения суммы периметров оснований Po1 и Po2 на апофему (высоту) трапеции Ap.
Например, для случая с четырехугольной правильной усеченной пирамидой эта формула перепишется в виде:
S4 = B2 + b2 + 2 × (B + b ) × Ap.
Где B, b — длины сторон большого и малого квадратных оснований соответственно.
Объем усеченной пирамиды
Для определения объема рассматриваемой фигуры необходимо знать ее высоту h, а также площади обоих оснований So1 и So2. Если указанные характеристики известны, тогда для определения объема усеченной пирамиды следует воспользоваться формулой:
V = 1/3 × h × (So1 + So2 + √ (So1 × So2)).
Например, для четырехугольной правильной фигуры, длины сторон оснований которой равны B и b, приходим к следующему выражению для объема:
V = 1/3 × h × (B2 + b2 + B × b).
Пример решения задачи
Рассмотрев, что такое усеченная пирамида, а также разобравшись с необходимыми для описания ее характеристик формулами, покажем, как их использовать на практике.
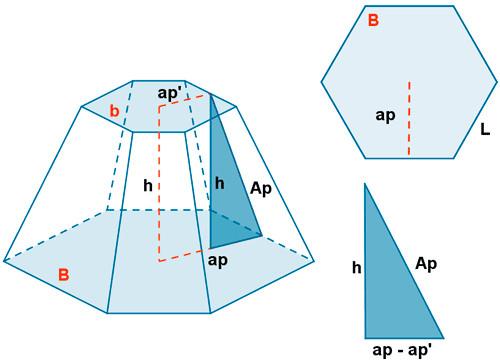
Предположим, что имеется шестиугольная усеченная фигура, которая показана ниже.
Необходимо рассчитать ее объем, если известны стороны оснований B и b и апофема Ap.
Для начала рассчитаем площадь каждого из оснований, которая соответствует площади правильного шестиугольника. Имеем:
Для определения объема необходимо вычислить через Ap высоту h фигуры. Рассматривая изображенный на рисунке прямоугольный треугольник и применяя теорему Пифагора, получаем:
h = √ (Ap2 — 3/4 × (B-b)2).
Тогда объем этой шестиугольной усеченной пирамиды будет равен:
V = √3/2 × √(Ap2 — 3/4 × (B-b)2) × (B2 + b2 + B × b).
Пирамиды индейцев майя
Если египетские пирамиды с точки зрения геометрии представляют собой правильные полные четырехугольные фигуры, то аналогичные сооружения индейцев майя являются четырехугольными усеченными пирамидами.
Эти памятники культуры, сохранившиеся до наших дней, некогда выполняли двойную роль для своих жителей: с одной стороны, они служили гробницей вождям, с другой же стороны, на их верхнем основании располагался храм, где жрецы поклонялись богам.
Источник
При изучении свойств фигур в трехмерном пространстве в рамках стереометрии часто приходится решать задачи на определение объема и площади поверхности. В данной статье покажем, как для усеченной пирамиды объем и площадь боковой поверхности вычислить, используя известные формулы.
Пирамида в геометрии
В геометрии обычной пирамидой называют фигуру в пространстве, которая построена на некотором плоском n-угольнике. Все вершины его соединены с одной точкой, расположенной вне плоскости многоугольника. Для примера приведем фото, где изображена пятиугольная пирамида.

Эта фигура образована гранями, вершинами и ребрами. Пятиугольная грань называется основанием. Остальные треугольные грани образуют боковую поверхность. Точка пересечения всех треугольников — это главная вершина пирамиды. Если из нее опустить перпендикуляр на основание, то возможны два варианта положения точки пересечения:
- в геометрическом центре, тогда пирамида называется прямой;
- не в геометрическом центре, тогда фигура будет наклонной.
Далее будем рассматривать только прямые фигуры с правильным n-угольным основанием.
Что это за фигура — усеченная пирамида?
Чтобы определить объем усеченной пирамиды, необходимо четко понимать, о какой фигуре конкретно идет речь. Внесем ясность в этот вопрос.
Предположим, что мы взяли секущую плоскость, которая параллельна основанию обычной пирамиды, и отсекли с помощью нее часть боковой поверхности. Если эту операцию проделать с изображенной выше пятиугольной пирамидой, то получится такая фигура, как на рисунке ниже.

Из фото видно, что эта пирамида имеет уже два основания, причем верхнее является подобным нижнему, но по размерам оно меньше. Боковая поверхность представлена уже не треугольниками, а трапециями. Они являются равнобедренными, а их число соответствует количеству сторон основания. Усеченная фигура не имеет главной вершины, как обычная пирамида, а ее высота определяется расстоянием между параллельными основаниями.
В общем случае, если рассматриваемая фигура образована n-угольными основаниями, она имеет n+2 грани, или стороны, 2*n вершин и 3*n ребер. То есть усеченная пирамида является многогранником.
Формула объема усеченной пирамиды
Напомним, что объем обычной пирамиды равен 1/3 произведения ее высоты и площади основания. Для усеченной пирамиды эта формула не подходит, поскольку она имеет два основания. А ее объем будет всегда меньше, чем аналогичная величина для обычной фигуры, из которой она получена.
Не вдаваясь в математические подробности получения выражения, приведем конечную формулу для объема усеченной пирамиды . Она записывается в следующем виде:
V = 1/3*h*(S1 + S2 + √(S1*S2))
Здесь S1 и S2 — площади нижнего и верхнего оснований соответственно, h — высота фигуры. Записанное выражение является справедливым не только для прямой правильной усеченной пирамиды, но и для любой фигуры данного класса. Причем независимо от вида многоугольников основания. Единственным условием, ограничивающим применение выражения для V, является необходимость параллельности друг другу оснований пирамиды.
Несколько важных выводов можно сделать, изучая свойства этой формулы. Так, если площадь верхнего основания равна нулю, тогда мы приходим к формуле для V обычной пирамиды. Если же площади оснований равны друг другу, то получаем формулу для объема призмы.
Как определить площадь боковой поверхности?
Знание характеристик усеченной пирамиды предполагает не только умение рассчитывать ее объем, но и знать, как определять площадь боковой поверхности.
Пирамида усеченная состоит из двух типов граней:
- равнобедренные трапеции;
- многоугольные основания.
Если в основаниях находится правильный многоугольник, то расчет его площади не представляет больших трудностей. Для этого нужно знать лишь длину стороны a и их количество n.
В случае с боковой поверхностью расчет ее площади предполагает определение этой величины для каждой из n трапеций. Если n-угольник является правильным, то формула для площади боковой поверхности принимает вид:
Sb = hb*n*(a1+a2)/2
Здесь hb — высота трапеции, которая называется апотемой фигуры. Величины a1 и a2 — это длины сторон правильных n-угольных оснований.
Для каждой правильной n-угольной усеченной пирамиды можно однозначно определить апотему hb через параметры a1 и a2 и высоту h фигуры.
Задача на вычисление объема и площади фигуры
Дана правильная треугольная усеченная пирамида. Известно, что ее высота h равна 10 см, а длины сторон оснований равны 5 см и 3 см. Чему равны объем усеченной пирамиды и площадь ее боковой поверхности?
Сначала вычислим величину V. Для этого следует найти площади равносторонних треугольников, находящихся в основаниях фигуры. Имеем:
S1 = √3/4*a12 = √3/4*52 = 10,825 см2;
S2 = √3/4*a22 = √3/4*32 = 3,897 см2
Подставляем данные в формулу для V, получаем искомый объем:
V = 1/3*10*(10,825 + 3,897 + √(10,825 *3,897 )) ≈ 70,72 см3
Чтобы определить боковую поверхность, следует знать длину апотемы hb. Рассматривая соответствующий прямоугольный треугольник внутри пирамиды, можно для него записать равенство:
hb = √((√3/6*(a1 — a2))2 + h2) ≈ 10,017 см
Значение апотемы и сторон треугольных оснований подставляем в выражение для Sb и получаем ответ:
Sb = hb*n*(a1+a2)/2 = 10,017*3*(5+3)/2 ≈ 120,2 см2
Таким образом, мы ответили на все вопросы задачи: V ≈ 70,72 см3, Sb ≈ 120,2 см2.
Объем усеченной пирамиды
Рассчитайте объем усеченной пирамиды в зависимости от ее высоты и площадей оснований.
Площадь основания 1
см2
Площадь основания 2
см2
Высота
см
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧮 Что такое калькулятор объема усеченной пирамиды?
Калькулятор объема усеченной пирамиды — это инструмент для расчета объема геометрического тела, которое представляет собой усеченную пирамиду.
Усеченная пирамида — это геометрическое тело, которое состоит из двух параллельных и равных многоугольников, называемых основаниями, и боковой поверхности, состоящей из параллельных трапеций. Объем усеченной пирамиды можно вычислить, зная ее высоту и площади оснований.
Калькулятор объема усеченной пирамиды предоставляет пользователю возможность ввести размеры оснований и высоту усеченной пирамиды, после чего вычисляет ее объем.
Как рассчитывается объем усеченной пирамиды?
Объем усеченной пирамиды можно рассчитать с помощью следующей формулы:
V = (1/3) * h * (A + sqrt(A*B) + B)
где V — объем усеченной пирамиды, h — высота усеченной пирамиды, sqrt — означает квадратный корень, A и B — площади большего и меньшего оснований соответственно.
Для расчета объема усеченной пирамиды необходимо знать высоту и площади ее оснований. Первым шагом необходимо определить площади большего и меньшего оснований. Для этого необходимо найти площадь каждого основания (например, площадь треугольника или многоугольника) и обозначить их A и B соответственно.
Затем необходимо найти высоту усеченной пирамиды, которая является расстоянием между плоскостями оснований. Высоту можно измерить прямым измерением или вычислить, зная расстояние между плоскостями оснований и угол между этим расстоянием и боковой гранью.
После этого можно использовать формулу для расчета объема усеченной пирамиды, подставив известные значения площадей оснований и высоты в формулу.
Для чего можно использовать калькулятор объема усеченной пирамиды?
Калькулятор объема усеченной пирамиды можно использовать для расчета объема данной геометрической фигуры, когда известны ее размеры. Это может быть полезно в различных областях, включая:
- Архитектуру и строительство: расчет объема усеченной пирамиды может быть полезен для расчета объема строительных материалов, таких как бетон или кирпич, необходимых для создания определенных форм.
- Производство: объем усеченной пирамиды может использоваться для расчета объема материала, необходимого для производства определенного изделия.
- Образование: расчет объема усеченной пирамиды может быть использован в качестве учебного материала в школах и университетах для изучения геометрии и математики.
- Хобби и ремесло: расчет объема усеченной пирамиды может быть полезен в различных хобби и ремеслах, таких как создание моделей или изготовление ювелирных изделий.
Усеченная пирамида как фигура
Усеченная пирамида является интересной геометрической фигурой, которая обладает несколькими уникальными свойствами:
- Усеченная пирамида имеет два плоских многоугольных основания, которые могут быть различной формы, но параллельны друг другу.
- В отличие от обычной пирамиды, усеченная пирамида может иметь наклонные боковые ребра, которые делают ее форму более сложной и необычной.
- Усеченная пирамида может использоваться в качестве модели для создания архитектурных конструкций, таких как купола, шатры, крыши зданий и т.д.
- Усеченные пирамиды используются в различных областях науки и техники, включая архитектуру, физику, инженерию, компьютерную графику и многие другие.
- Усеченная пирамида может быть использована как основа для создания различных предметов декора и искусства, таких как светильники, вазы, канделябры и т.д.
- Усеченная пирамида может быть использована для создания различных игрушек и головоломок, что делает ее интересной не только для учебных, но и для развлекательных целей.
❓Вопросы и ответы
Вот некоторые часто задаваемые вопросы и ответы, связанные с калькулятором объема усеченной пирамиды:
Что такое усеченная пирамида?
Усеченная пирамида — это геометрическая фигура, которая имеет два параллельных многоугольных основания и наклонные боковые грани.
Как рассчитать объем усеченной пирамиды?
Объем усеченной пирамиды можно вычислить с помощью специальной формулы: V = (1/3) * h * (S1 + S2 + sqrt(S1 * S2)), где h — высота усеченной пирамиды, S1 и S2 — площади оснований, sqrt — квадратный корень.
Как использовать калькулятор объема усеченной пирамиды?
Введите значения высоты усеченной пирамиды, площадей ее оснований и нажмите кнопку «Вычислить». Калькулятор автоматически рассчитает объем усеченной пирамиды для вас.
Какие единицы измерения используются при вычислении объема усеченной пирамиды?
Объем усеченной пирамиды может быть выражен в кубических единицах измерения, таких как кубические метры, кубические сантиметры, кубические дюймы и т.д.
Для чего можно использовать калькулятор объема усеченной пирамиды?
Калькулятор объема усеченной пирамиды может быть полезен в образовательных целях, а также для проектирования и расчета объема различных конструкций и изделий.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Фигура конус
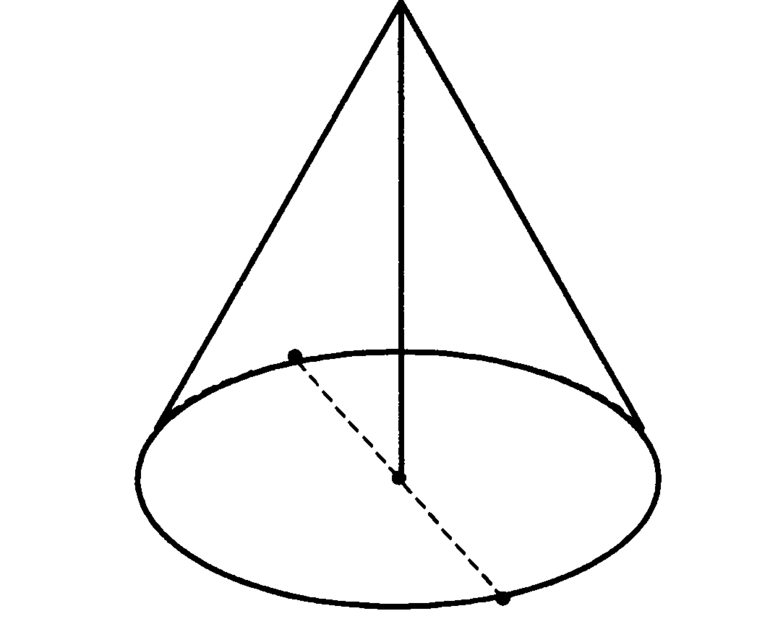
Прежде чем отвечать на вопрос о том, что это — усеченный конус, необходимо познакомиться с фигурой, от которой он образован. Конусом в геометрии принято называть фигуру, получаемую с помощью соединения прямыми отрезками некоторой точки пространства со всеми точками заданной кривой. Точка пространства не должна лежать в плоскости кривой, она называется вершиной конуса. Соединяющие отрезки — это образующие фигуры, а плоская кривая — это направляющая. Она ограничивает основание конуса. В свою очередь, совокупность всех образующих называется конической поверхностью. Конус, основанием которого является круг, показан на рисунке.
Вам будет интересно:«Земляк» – это соотечественник и поддержка на чужбине
Расстояние между вершиной фигуры и основанием называется высотой. Если соответствующий перпендикуляр пересекает основание в геометрическом центре, то фигуру называют прямой.
Вам будет интересно:Полиакриловая кислота: способ получения, свойства, структура и практическое применение
Дальше в статье покажем, как, используя прямой круглый конус, получить усеченную фигуру.
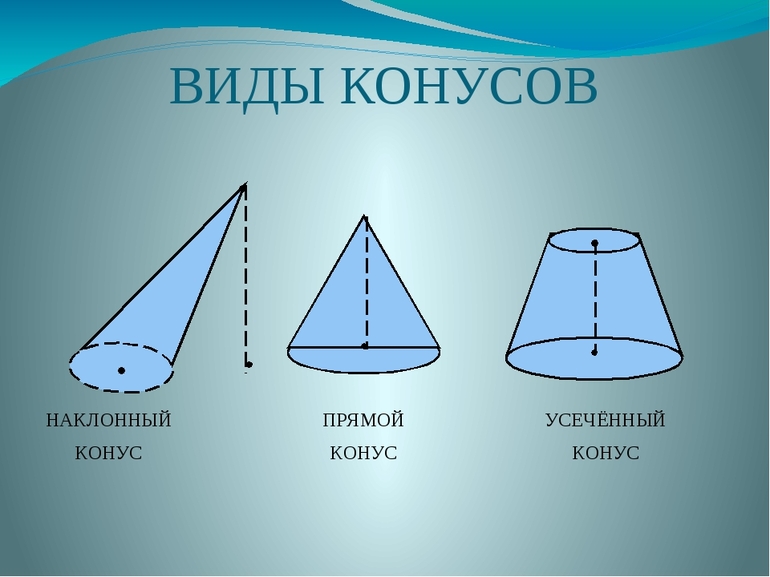
Разновидности конусов
В геометрии насчитывают почти десяток типов конусов:
- Прямой круговой – нижняя грань представлена кругом – фигурой, имеющей центр симметрии. Ось, которая проходит от вершины к центру основания, перпендикулярна плоскости последнего.
- Наклонный либо косой – проекция вершины на нижнюю поверхность не совпадает с его центром.
- Круговой – с кругом в центре.
- Прямой – нижняя поверхность представлена кругом либо эллипсом. Центр нижней поверхности совпадает с проекцией вершины на неё.
- Гиперболический, параболический, эллиптический – опираются на соответствующие фигуры.
- Равносторонний – образующая равна диаметру нижней поверхности.
- Усеченный – ограниченный плоскостью, параллельной основанию. Располагается между ним и вершиной геометрического тела.
- Двойной – два одинаковых тела имеют общую вершину или основание и ось – проходит через оба тела.
Усеченный конус и способы его получения
Предположим, что у нас имеется фигура, которая была показана в предыдущем пункте. Возьмем плоскость, параллельную основанию конуса, и отсечем с помощью нее вершину фигуры. Этот процесс показан на рисунке.
Образованная над плоскостью фигура является конусом, а вот фигура под плоскостью — это конус усеченный.
Существует еще один способ получения рассматриваемой фигуры. Предположим, что имеется некоторая трапеция с двумя прямыми углами. Если вращать эту трапецию вокруг стороны, к которой прямые углы прилегают, то она опишет поверхность усеченного конуса. Этот способ получения фигуры демонстрирует схема ниже.
Сторона трапеции, вокруг которой выполнялось вращение, будет являться осью усеченного конуса. Отрезок, который на оси отсекают два основания фигуры, называется высотой. На рисунке отмечены образующая g и радиусы оснований конуса усеченного r и r’.
Наконец, третий способ получения усеченного конуса заключается в увеличении количества ребер усеченной пирамиды до бесконечного числа. Во время этого процесса пирамида постепенно перейдет в конус.
Любопытно отметить, что форма рассматриваемой геометрической фигуры в первом приближении в природе характерна для действующего вулкана, что отчетливо видно на следующей фотографии.
Понятие
Принципы образования геометрического тела просты. Представим две параллельные плоскости a и a1. С расположенной на первой точке перпендикуляр опускается на вторую. Точка на a1 – основание перпендикуляра, она является центром круга. Если соединить точку на плоскости a с каждой точкой круга на a1, получится конус. Основание перпендикуляра его – высота.
Второй вариант образования рассматриваемого геометрического тела: прямоугольный треугольник вращается вокруг катета по или против часовой стрелки. Катет, ставший осью, будет высотой конуса, лежащий в основании – диаметром нижней поверхности, гипотенуза – образующей.
Длина образующих одинакова, их совокупность называется боковой поверхностью. Квадрат длины образующей равняется сумме квадратов высоты и радиуса основания (из теоремы Пифагора): l2 = h2 + r2. Отсюда
Элементы фигуры и ее линейные характеристики
Усеченный конус — это пространственная фигура, состоящая из трех поверхностей. Две из них представляют собой круглые основания (верхнее и нижнее) и одна — боковую поверхность. В отличие от многогранников, рассматриваемая фигура не имеет вершин и граней.
Важными параметрами конуса усеченного являются радиусы каждого из оснований. Будем больший радиус обозначать r1, меньший — r2. Помимо радиусов фигуры, для ее однозначного определения необходимо знать либо высоту h, либо образующую g. Указанные параметры связаны математически следующим равенством:
g2 = h2 + (r1 — r2)2
Все четыре параметра используются для определения площади поверхности и объема.
Лист 5 Сечение конуса плоскостью (ТТП, Дизайн, Технология и доп. Обр.)
⇐ ПредыдущаяСтр 3 из 3
Задача 6
Построить три проекции конуса, усеченного плоскостью Р, натуральную величину сечения, развертку и изометрию (рис 9).
Координаты точек взять из таблицы 5.
Таблица 5
| № варианта | α г рад | А |
| 1 | 30 | 63 |
| 2 | 45 | 50 |
| 3 | 45 | 45 |
| 4 | 40 | 55 |
| 5 | 35 | 60 |
| 6 | 55 | 40 |
| 7 | 45 | 55 |
| 8 | 40 | 50 |
| 9 | 25 | 63 |
| 10 | 30 | 45 |
Указания к решению задачи
1. В левой половине листа формата A3 намечаются оси координат, и в соответствии с данными своего варианта определяется центр окружности радиуса R основания конуса вращения в горизонтальной плоскости проекций. На вертикальной оси на расстоянии h (88 мм) от плоскости уровня и выше ее определяется вершина конуса вращения. Далее определяется секущая плоскость.
2. Натуральную величину фигуры сечения находим методом введения дополнительной плоскости проекций П4 фронтально проецирующей и параллельной плоскости Р.
3. Построение развертки начинаем с построения полной боковой поверхности. Основание делим на 12 частей, на ней откладываем точки линий пересечения. Точки соединяем плавной кривой. К развертке боковой поверхности присоединяем фигуру сечения и основание.
4. Аксонометрическую проекцию усеченной части конуса строим по координатам. (ось Z совмещаем с SО). Основание конуса – овал в изометрии.
Чертеж обводят, линию сечения обводят цветной пастой. Все вспомогательные линии построения сохранить и показать тонкими сплошными линиями.
Рис. 9
Лист 6 Пересечение многогранников (ТТП, Дизайн, Технология и доп. Обр.)
Задача 7
По двум проекциям геометрических тел построить третью проекцию и изометрию (рис 10). Построить линию взаимного пересечения этих тел. На горизонтальной проекции линия взаимного пересечения тел не показана.
Рис. 10
Варианты задания:
Лист 7 Шрифты и линии (ТТП, Дизайн)
В левой части формата А3 начертить все типы линий. Перечертить фигуру и заштриховать ее.
В правой части формата А3 шрифтом №10 написать заглавные и строчные буквы алфавита, цифры. Ниже этих букв, седьмым номером шрифта, написать предложение, состоящее из 7 слов (поговорка, афоризм).
Задание выполняется в соответствии с образцом (рис. 1), размеры не проставляются.
Рис. 1
Лист 8 Деление окружности. Сопряжения (ТТП)
В правой части формата А3 вычертить контуры деталей своего варианта с простановкой размеров, и применяя правила деления окружности на равные части.
Варианты задания:
В левой части формата А3 вычертить контуры деталей своего варианта с простановкой размеров, и применяя правила построения сопряжений.
Варианты задания:
⇐ Предыдущая3
Поверхность усеченного конуса
Как отмечалось, состоит поверхность фигуры из трех частей. Если отрезать каждое из оснований от фигуры, а затем вдоль образующей разрезать и развернуть боковую поверхность, то мы получим развертку усеченного конуса. Рисунок ниже показывает, как она выглядит.
Площади оснований усеченного конуса находятся по простой формуле для соответствующей величины круга:
So1 = pi × r12;
So2 = pi × r22
С площадью боковой поверхности дело обстоит несколько сложнее. Можно заметить, что она представляет собой сектор круга, некоего радиуса G, у которого вырезали центральную часть радиусом G-g. Если это учесть, то можно получить формулу для площади боковой поверхности Sb. Здесь ограничимся лишь приведением конечного выражения:
Sb = pi × (r1 + r2) × g
Это выражение можно записать через радиусы и высоту h, однако тогда оно будет иметь несколько громоздкий вид.
Складывая записанные выражения, получаем формулу для определения площади S всей поверхности усеченного конуса:
S = So1 + So2 + Sb = pi × r12 + pi × r22 + pi × (r1 + r2) × g =
= pi × (r12 + r22 + (r1 + r2) × g)
Площадь
Под площадью подразумевают количество квадратов со стороной единица, помещающихся на определенной поверхности.
Площадь прямого конуса определяется по формуле:
- основания – Sосн = πr2; r – радиус;
- боковой поверхности – Sбп = πrl; l – длина;
- полная – S = Sосн + Sбп = πr2 + πrl = πr (r + l).
Пример:
- диаметр равен 12 см;
- длина образующей – 10 см.
Решение.
Радиус – это половина диаметра: 12/2 = 6 см.
Подставим значения в выражение: S = πr (r + l).
Получим: S = π * 6 *(6 + 10) = 96 π ≈ 301,584 см2.
Объем фигуры
Как и любая фигура в пространстве, усеченный конус тоже обладает некоторым объемом. Этот объем ограничен двумя основаниями и боковой поверхностью. Здесь не будем приводить подробный вывод соответствующей формулы для V. Запишем, как и в случае с площадью поверхности, лишь конечный результат:
V = h × pi / 3 × (r12 + r22 + r1 × r2)
Эта формула, в отличие от выражения для площади S, в качестве параметров содержит радиусы усеченного конуса и его высоту.
Далее в статье покажем, как следует использовать приведенные формулы для решения конкретной геометрической задачи.
Объем усечённого конуса
Объем – пространство, занимаемое геометрическим телом. Численное значение указывает на количество кубиков с гранью единица, помещающихся в конусе. Объем тела вычисляется как треть произведения площади основания на его высоту.
Основание – круг, его поверхность рассчитывается по формуле: Sосн = πr2. После подстановки получим:
.
Пример: вычислить объем тела: r = 6 см, h = 9 см. Ставим значения в формулу, пошагово упрощаем выражение.
Если известен диаметр, разделите его на два: .
Вычислим объем усеченного конуса. Для понимания, от полного объема исходного тела нужно отнять значение отрезанного параллельной нижней грани плоскостью.
Формула объема усеченного конуса:
Задача 5
Рис. 8. Вращаемый треугольник
Рис. 9. Тело, полученное при вращении равнобедренного треугольника
Равнобедренный треугольник, боковая сторона которого равна , а угол при основании равен , вращается вокруг своего основания (см. рис. 8). Найти площадь поверхности полученного при вращении тела (см. рис. 9).
Решение
Рис. 10. Два равных конуса
Если провести в треугольнике высоту из вершины, то получается два прямоугольных треугольника, вращая которые мы получаем два равных конуса, прилегающих друг к другу основаниями (см. рис. 10).
Значит, площадь поверхности искомого тела равна удвоенной площади боковой поверхности любого из конусов. Таким образом, нам надо найти радиус основания и образующую конуса (см. рис. 11).
Рис. 11. Иллюстрация к последнему шагу
Радиус основания конуса равен высоте исходного треугольника, а образующая – боковой стороне. Очевидно, высота равна , а значит, , таким образом, окончательный ответ: .
Ответ: .