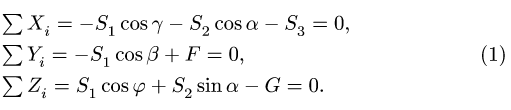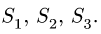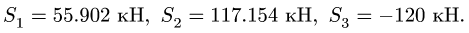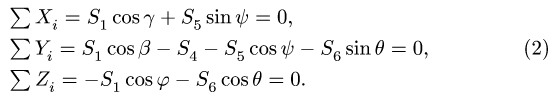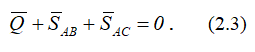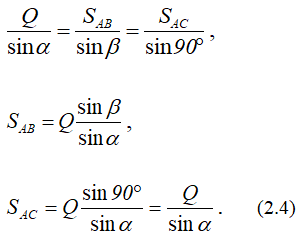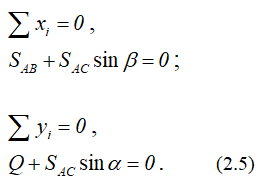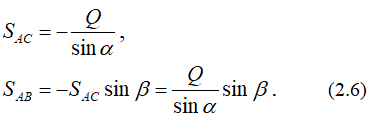Содержание:
Расчет ферм:
При устройстве перекрытий, постройке мостов, кранов, мачт для высоковольтных линий и т. п. применяются конструкции, называемые фермами.
Фермой называется геометрически неизменяемая система, состоящая из невесомых стержней, соединенных между собой по концам шарнирами. Места соединения стержней между собой называются узлами фермы.
Обычно в фермах соединение стержней в узлах осуществляется при помощи клепки или сварки, шарнирное же соединение стержней вводится лишь для облегчения расчета ферм, что приводит к сравнительно небольшим ошибкам в вычислении по сравнению с действительными конструкциями.
Фермы, у которых оси всех стержней расположены в одной плоскости, называются плоскими. В дальнейшем мы ограничимся рассмотрением плоских ферм.
Всякая ферма состоит из ряда стержневых треугольников, соединенных в узлах шарнирно (рис. 79).
Рис. 79.
Для образования фермы мы должны взять основной треугольник, хотя бы abc, и к нему последовательно присоединять каждый узел d, е и т. д. двумя стержнями. Если ферма состоит из
При расчете фермы, т. е. при определении усилий во всех ее стержнях, мы можем для каждого узла составить два уравнения равновесия, а для 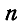
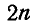
Отсюда следует, что число неизвестных усилий, определяемое числом стержней, сложение с числом опорных реакций не должно превышать общего числа уравнений статики 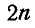
Для определения усилий в стержнях ферм обычно применяют один из следующих трех способов: последовательное вырезание узлов, построение диаграммы Кремона, проведение сквозных сечений (Риттера).
При применении каждого из перечисленных способов следует предварительно по заданным силам, приложенным к ферме, определить опорные реакции (аналитически или графически) и только после этого переходить к определению усилий в стержнях фермы.
Определение усилий по способу последовательного вырезания узлов
Определение усилий по способу последовательного вырезания узлов заключается в том, что последовательно рассматривают равновесие каждого узла фермы и для рассматриваемого узла либо составляют два уравнения равновесия в форме 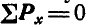
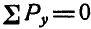
При этом порядок рассмотрения равновесия узлов безразличен, лишь бы в рассматриваемом узле число неизвестных усилий не превышало двух.
Выясним применение этого способа на отдельных примерах.
Задача №1
Найти усилия 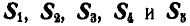
Рис. 80.
Решение. Начнем с рассмотрения равновесия узла А, так как здесь сходятся два неизвестных усилия. Вырежем узел А и взамен пересеченных стержней введем силы 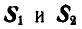
Вырежем теперь узел В и рассмотрим его равновесие (рис. 80, в):
откуда получаем:
Переходим к рассмотрению равновесия узла С (рис. 80, г):
откуда находим:
Составляя уравнения равновесия для точки D (рис. 80, д), имеем:
откуда
Для усилия 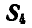
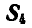
Правильное направление стрелок усилий показано на рисунке 80, а.
Иногда при определении усилий в стержнях полезно сразу выделить те стержни, усилия в которых равны нулю (нулевые стержни). Из рассмотрений равновесия узлов А и С (рис. 80, б и. 80, г) заключаем:
1. Если имеется узел А, в котором сходятся два стержня, то при отсутствии других сил, приложенных к узлу, усилия в этих стержнях равны нулю.
2. Если имеется узел С, где сходятся три стержня, из которых два направлены по одной прямой, а третий примыкает к узлу под любым углом, то при отсутствии других сил, приложенных к узлу, усилие в третьем стержне равно нулю. На основании этого можно сказать, что усилия в стержнях 1, 2, 3, 4, 5 и 6 фермы (рис. 79) равны нулю.
Задача №2
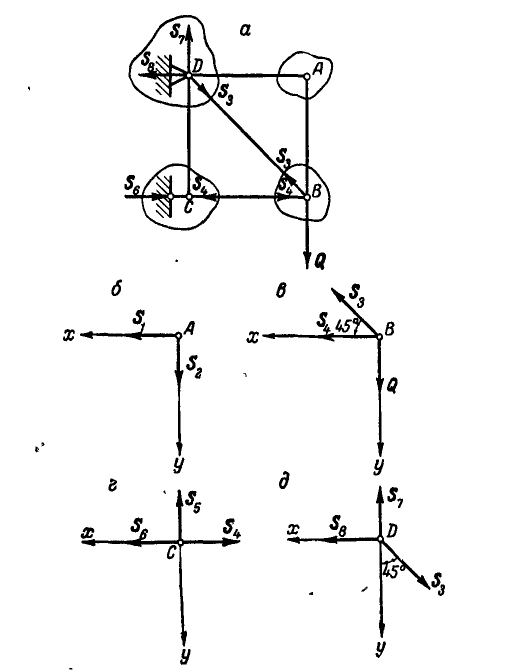
Сцепка состоит из четырех тросов АО, ВО, АС и ВС, образующих квадрат (рис. 81, а).
Между точками А и В по диагонали квадрата вставлен брус, а в точках А, В и С приложены вертикальные силы Q = 500 кГ каждая. Определить натяжения 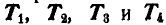
Решение. Из рассмотрения равновесия точки С (рис. 81, б) имеем:
откуда:
Переходим к рассмотрению равновесия узла А (рис. 81, в):
откуда
Рис. 81.
В силу симметрии узлов А и В заключаем, что 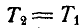
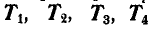
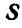
Задача №3
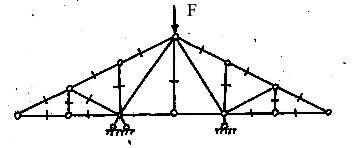
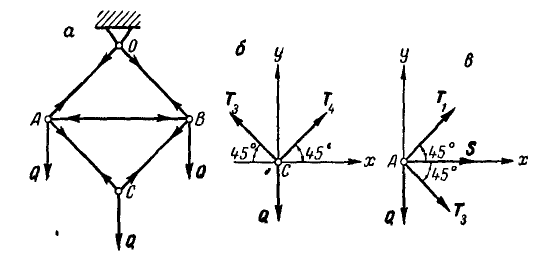
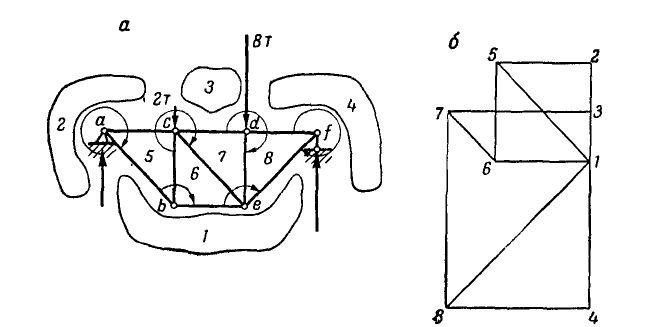
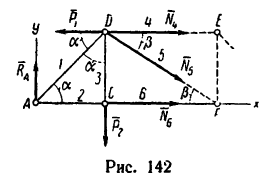
В точках А и F шарнирной стержневой системы (рис. 82, а), внешний контур которой совпадает со сторонами правильного шестиугольника, приложены силы 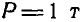
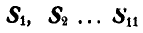
Рис. 82.
Решение. Эту задачу проще всего решить геометрическим способом, построив для каждого из узлов замкнутый треугольник сил. Рассмотрим сначала равновесие точки А (можно F). Отложим в выбранном масштабе силу Р (рис. 82, б) и из начала и конца этой силы проведем направления, параллельные стержням 1 и 6, до их взаимного пересечения. В полученном треугольнике равновесия стрелки сил 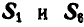
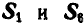
При построении треугольника равновесия для точки В известной нам силой является реакция 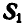
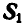
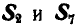
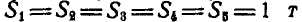
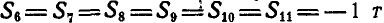
Задача №4
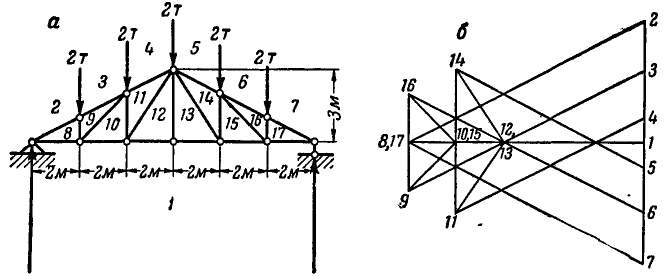
Способом последовательного вырезания узлов определить усилия во всех стержнях ферм (рис. 83 и 84).
Рис. 83. Рис. 84.
Ответ (к рис. 83).
Таблица 1
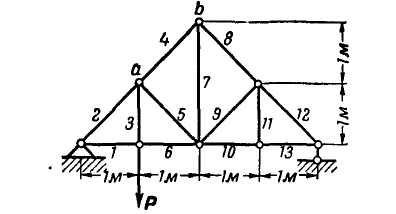
Ответ (к рис. 84).
Таблица 2
Определение усилий в стержнях ферм по способу построения диаграммы Кремона
Идея этого графического способа проста и заключается в построении для узлов фермы, находящихся в равновесии, замкнутых многоугольников сил, образующих диаграмму.
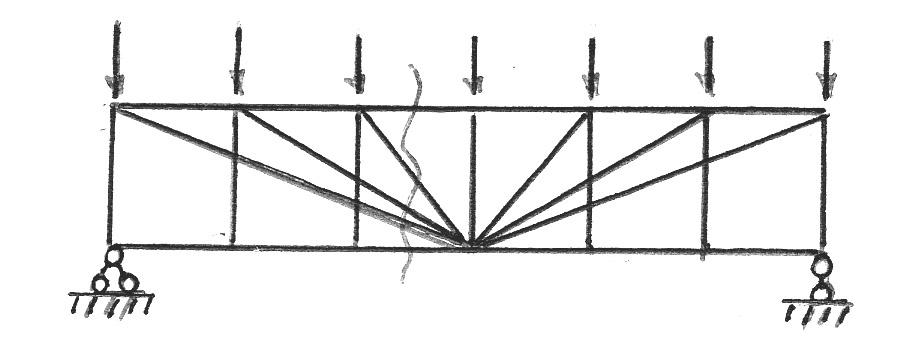
Пусть требуется найти усилия во всех стержнях фермы (рис. 85, а) при действии на нее заданных сил 2 т и 8 т. Известными нам способами находим, что левая опорная реакция равна 4 т, а правая 6 т.
Для облегчения построения диаграммы введем в рассмотрение внешние и внутренние поля. Под внешними полями будем понимать части плоскости, ограниченные с боков внешними силами (заданными и реактивными) и внешним контуром фермы, под внутренними полями — части плоскости, ограниченные стержнями фермы.
Рис. 85.
Условимся нумерацию внешних полей 1, 2, 3 и 4 (рис. 85, а) производить по направлению движения стрелки часов, внутренних 5, 6, 7, 8 — слева направо, а усилия, сходящиеся в каждом узле обозначать двойными цифрами смежных полей, производя обход усилий в каждом узле по часовой стрелке. Так, например, в узле а сходятся три усилия: 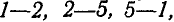
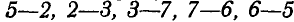
Выбрав масштаб сил, например 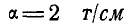
Построение диаграммы следует начинать для того узла, в котором сходятся не более двух стержней. В нашем случае такими узлами являются 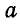
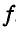
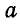
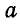
Теперь можно перейти к следующему узлу, где сходятся два неизвестных усилия; таким узлом является 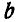
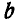
Переходим к узлу с. Здесь сходятся усилия 6—5, 5—2, 2—3, имеющиеся на диаграмме, и неизвестные 3—7 и 7—6. Проводим из точки 3 диаграммы направление, параллельное стержню 3—7, а из точки 6 направление, параллельное стержню 7—6; в пересечении этих направлений получаем на диаграмме точку 7. Подобные построения можно провести для остальных узлов. Узел 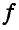
Имея диаграмму Кремона (рис. 85, б), можно:
1. Проверять правильность построенной диаграммы, основываясь на том, что многоугольник сил для каждого узла должен быть замкнут. Возьмем, например, узел d, в котором сходятся усилия 7—3, 3—4, 4—8, 8—7. Мы видим, что эти усилия на диаграмме образуют замкнутый многоугольник.
2. Определять величину и знак усилия в любом стержне, примыкающем к какому-либо узлу. Так, например, если возьмем стержень 3—7, примыкающий к узлу с (если бы мы переставили цифры и рассматривали стержень 7—3, то тогда мы обязаны были бы его отнести к узлу d), то на диаграмме величина усилия, возникающего в этом стержне, выражается отрезком 3—7, умноженным на масштаб, а направление будет к узлу с, так как на диаграмме усилие 3—7 читается от 3 к 7, т. е. справа налево. Точно так же усилие в стержне 7—6 изобразится на диаграмме отрезком 7—6, умноженным на масштаб α , а направление усилия будет от узла с, так как при чтении усилия 7—6 на диаграмме оно направлено от 7 к 6, т. е. сверху вниз по диагонали. Следовательно, в первом случае мы имеем сжатие (—), во втором — растяжение (+).
Задача №5
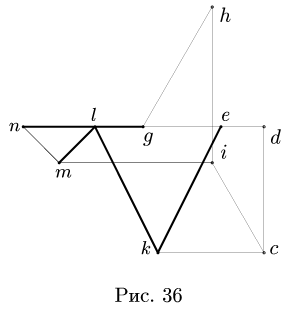
Определить усилия в стержнях ферм путем построения диаграммы Кремона (рис. 86, а и 87, а).
Рис. 86.
Рис. 87.
Решение. На рисунках 86, б и 87, б приведено построение диаграмм.
Определение усилий в стержнях ферм по способу сквозных сечений
Особенность этого способа состоит в том, что он позволяет определять усилие в любом стержне фермы, не определяя усилий в остальных стержнях, что во многих случаях является удобным.
Выясним применение этого способа на отдельном примере.
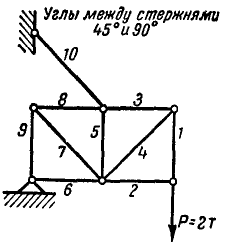
Пусть дана ферма (рис. 88, а), стержни которой образуют между собой углы в 45° и 90°. Определим сначала величины опорных реакций аналитически или способом веревочного многоугольника. Нетрудно видеть, что
Пронумеровав стержни, можно перейти к определению усилий, возникающих в стержнях, по способу сквозных сечений. Положим, требуется найти усилие 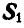
Рассмотрим теперь равновесие одной из частей фермы, расположенной слева или справа от проведенного сечения. В данной задаче удобнее выделить левую часть, так как на нее действует меньше сил (рис. 88, б).
Взамен отброшенной правой части прикладываем реакции стержней 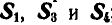
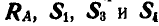

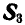
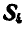

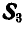
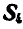
Рис. 88.
Нетрудно видеть, что таким. уравнением является уравнение моментов относительно той точки, где пересекаются линии действия усилий 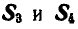
откуда
Чтобы определить усилие 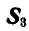
откуда
Для определения усилия 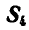
откуда
Знак минус указывает на то, что стержень 4 сжат,
Точки 1, 3; 3, 4 и 1, 4, выбранные таким образом, приводят нас к уравнениям равновесия (36, б).
При определении усилия 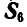
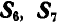
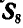
Для определения усилия 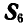
откуда
При определении усилия в стержне 7 следовало бы составить уравнение моментов относительно точки 6, 8, пересечения стержней 6 и 8, но эти стержни параллельны и точка 6, 8 получается в бесконечности; в этом случае вместо уравнения моментов составляют уравнение проекций на ось, перпендикулярную к линиям действия тех реакций стержней, которые параллельны:
откуда
Подобным же способом можно определить усилия и в остальных стержнях.
Преимущество изложенного способа заключается в том, что здесь мы можем определить усилие в любом стержне, не определяя усилий в остальных стержнях.
Рис. 89.
Задача №6
Определить по способу сквозных сечений усилия во всех стержнях фермы (рис. 89).
Указание: предварительно определяем реакцию 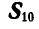
Ответ (к рис. 89) см. в таблице 3.
Таблица 3
Задача №7
По известному усилию в стержне 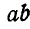
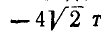
Рис. 90.
Ответ (к рис. 90) см. таблицу 4.
Таблица 4
Статически определимые фермы. Методы вырезания узлов и сквозного сечения
Плоская или пространственная неизменяемая конструкция, составленная из шарнирно соединенных между собой стержней, называется фермой.
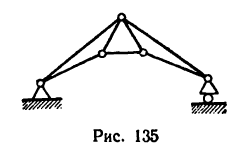
На рис. 135 изображена простая плоская ферма (пример пространственной фермы приведен в § 19-4).
Если число узлов (шарниров) фермы n, а число стержней k, то в простой плоской ферме соблюдается условие
k=2n + 3
Ферма называется статически определимой, если усилия во всех стержнях фермы, нагруженной в шарнирах, можно определить при помощи уравнений равновесия.
Все. плоские простые фермы статически определимы.
Для определения усилий в стержнях ферм употребляются графические или аналитические методы. Рассмотрим только аналитические методы: метод вырезания узлов (задача 103-17) и метод сквозного сечения—метод Риттера (задача 104-17).
При использовании метода вырезания узлов необходимо придерживаться следующего порядка:
- а) выяснить, какие нагрузки действуют на ферму, как они направлены и где приложены, а затем определить реакции связей, используя уравнения равновесия Правильность этой части решения нужно обязательно проверить: для проверки можно использовать любое дополнительно составленное уравнение равновесия;
- б) затем следует определить усилия в стержнях фермы, начиная с того узла, на который действуют не более двух неизвестных сил, так как в каждом случае на узел действует система сходящихся сил и, следовательно, для одного узла можно составить лишь два уравнения равновесия;
- в) вырезав узел, необходимо заменить действие на узел отброшенной части фермы усилиями, действующими вдоль стержней, считая при этом, что все стержни растянуты, а затем составить уравнения равновесия;
- г) путем перехода от узла к узлу определяют усилия во всех стержнях, один из узлов при этом остается нерассмотренным; составив уравнения равновесия для этого узла, можно проверить правильность решения задачи.
При определении усилий в стержнях ферм по методу сквозного сечения необходимо придерживаться следующего порядка:
- а) прежде всего, так же как и при методе вырезания узлов, выявив все нагрузки, определить реакции опор;
- б) мысленно разрезать фермы на две части таким образом, чтобы разрез проходил не более чем через три стержня, усилия в которых неизвестны»1, и, отбросив одну из частей, заменить действие отброшенной части на оставшуюся усилиями, направленными вдоль стержней, предполагая при этом, что все разрезанные стержни (с неизвестными усилиями) растянуты;
- в) составить три уравнения равновесия; при выборе направлений осей проекций, а также центра моментов нужно исходить из того, чтобы в каждое из уравнений по возможности входило не более одной неизвестной силы.
Задача №8
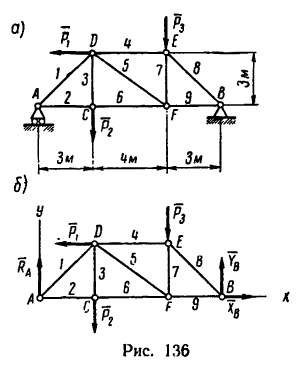
Определить усилия в стержнях фермы, нагруженной, как показано на рис. 136, а, тремя силами: 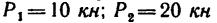
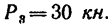
Решение — методом вырезания узлов.
1. Освободим ферму от связей и заменим связи их реакциями. Действие подвижного шарнира А заменим реакцией 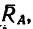
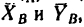
Составим три уравнения равновесия:
Подставив в эти уравнения числовые значения и решив находим (вычисления рекомендуем произвести самостоятельно):
* При разрезании фермы через четыре и большее число стержней образуется плоская система сил с четырьмя или соответственно большим числом неизвестных. Так как для произвольной плоской системы сил можно составить только три уравнения равновесия, задачу решить нельзя.
Для проверки можно использовать уравнение проекций сил на ось у или уравнение моментов сил относительно точки С (или D, или Е, или F).
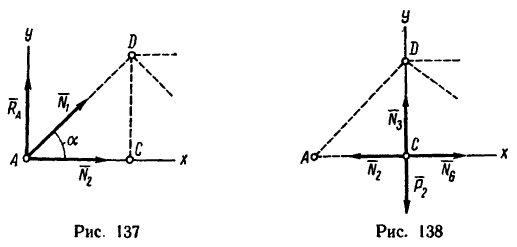
2. Вырежем узел А, заменив действие на узел отброшенной части фермы силами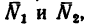
силы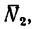
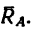
Из уравнения (2)
(стержень 1 сжат).
Из уравнения (1)
(стержень 2 растянут).
3. Вырежем узел С, заменив действие на узел отброшенной части фермы силами 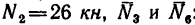
Отсюда
(стержень 6 растянут);
(стержень 3 растянут).
4. Вырежем узел D. В этом случае узел находится в равновесии иод действием пяти сил, три из них известны: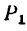
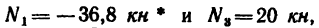
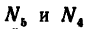
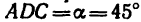
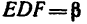
определить, что 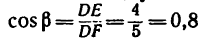
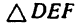
FE=3 л, катет DЕ = 4 м и, следовательно, гипотенуза DF=5 м), a
Составим уравнение равновесия:
Из уравнения (6)
(стержень 5 растянут).
Из уравнения (5)
(стержень 4 сжат).
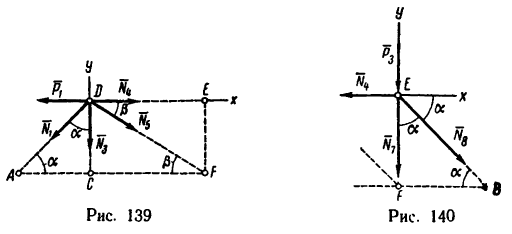
5. Вырежем узел Е, к которому приложены четыре силы: две из них известны (
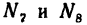
Расположив оси проекций, как показано на рис. 140, и замечая, что угол 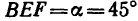
* Хотя из рассмотрения условия равновесия узла А установлено, что усилие в стержне 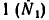
Из уравнения (7)
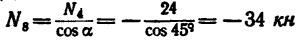
Из уравнения (8)
(стержень 7 сжат).
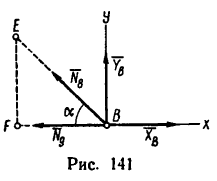
6. Вырежем узел В, к которому приложены четыре силы: реакции 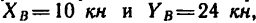

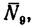
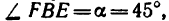
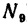
из которого
(стержень 9 растянут).
Усилия, возникающие во всех стержнях под действием внешних нагрузок, определены. Теперь_ рассмотрим узел F. Вырезав этот узел и составив для сил 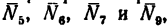
Найденные значения усилий в стержнях целесообразно представить в виде таблицы:
Задача №9
Определить усилия в стержнях 4, 5 и 6 фермы, нагруженной тремя силами: 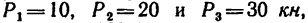
Решение.
1. Так же как и при решении методом вырезания узлов, прежде всего определяем реакции опор; в данном случае они те же, что и в предыдущем примере:
2. Разрежем ферму через стержни 4, 5 и 6 и, отбросив правую ее часть, заменим действие правой части на левую силами 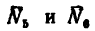
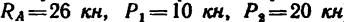
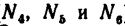
3. Составим три уравнения равновесия:
Из уравнения (1)
(стержень 5 растянут).
Из уравнения (2)
(стержень 6 растянут).
Из уравнения (3)
(стержень 4 сжат).
Сравнивая найденные числовые значения усилий в 4, 5 и 6 стержнях фермы с теми, которые для этих же стержней получены в задаче 103-17, видим, что они одинаковы.
Правильность решения здесь можно проверить, составив уравнение проекций сил на ось х. Для проверки это уравнение вполне надежно, так как в него входят все три искомые силы. Проверку решения этим способом рекомендуется произвести самостоятельно.
- Заказать решение задач по теоретической механике
Ферма и аналитические методы расчета
Постановка задачи:
Плоская ферма опирается на неподвижный и подвижный шарниры. К узлам фермы приложены нагрузки. Найти усилия в стержнях фермы методом Риттера
Эта задача является усложненным вариантом задачи, где усилия в стержнях можно было легко определить только из уравнений проекций, не находя реакции опор и не привлекая понятие момента силы. Аналогично можно поступить и в этой задаче, однако порядок системы линейных уравнений, описывающей равновесие всех узлов, будет велик, поэтому, во-первых, надежно решить такую систему можно только с помощью компьютера, во-вторых, таким образом будет проделана лишняя работа, так как система уравнений содержит усилия всех стержней, в том числе и тех, которые по условию задачи не требуется определять. Поэтому для решения сложных ферм, содержащих большое число стержней, применим метод Риттера, основная идея которого — независимое определение усилий в стержнях. Эту же идею можно с успехом применять и в других задачах статики.
План решения:
1. Освобождаем ферму от внешних связей. Действие опорных шарниров заменяем их реакциями. Для определения реакций опор составляем три уравнения равновесия.
2. Проверяем найденные реакции, составляя еще одно уравнение равновесия фермы.
3. В тех стержнях, где это возможно, усилия находим методом Риттера
Рассматриваем равновесие одной из частей фермы (как правило, где меньше нагрузок). Для стержней, усилия в которых необходимо определить, находим точки Риттера (моментные точки). Они являются точками попарного пересечения линий действия сил в рассеченных стержнях. Искомые усилия определяем из уравнений моментов рассматриваемой части относительно точек Риттера.
Если два стержня в сечении параллельны, то точки Риттера для третьего стержня не существует, и для определения усилия в нем необходимо составить уравнение проекций на ось, перпендикулярную параллельным стержням.
В уравнение метода Риттера всегда входит усилие только одного стержня. Это позволяет искать усилия независимо одно от другого,
уменьшая тем самым возможность ошибок и избегая накопления неизбежных погрешностей округления в численных расчетах.
4. Определяем усилия методом вырезания узлов. Этот метод применяют в тех случаях, когда сечения Риттера для нужного стержня не существует. Вырезаем узел фермы, к которому подходит стержень с искомым усилием. Выбираем оси и составляем уравнения равновесия узла в проекциях. Решаем уравнения относительно искомого усилия. Если к узлу подходит более двух стержней с неизвестными усилиями, то метод вырезания узлов можно комбинировать с методом Риттера.
Задача №10
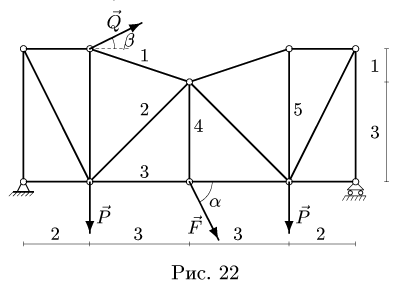
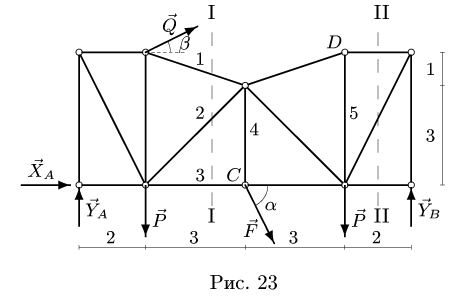
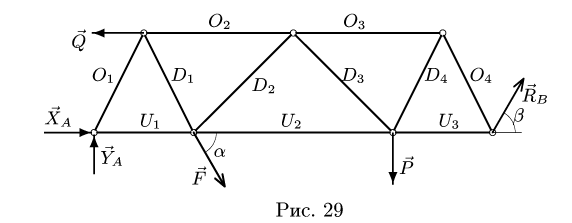
Плоская ферма опирается на неподвижный и подвижный шарниры (рис. 22). К узлам фермы приложены две вертикальные нагрузки Р — 90 кН и две наклонные 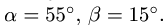
Решение
1. Освобождаем ферму от внешних связей. Действие опор заменяем их реакциями. Левую (неподвижную) шарнирную опору заменяем двумя составляющими реакции 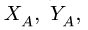
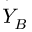
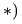
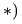
Система уравнений состоит из трех независимых друг от друга уравнений, решение которых легко найти, подставив численные значения нагрузок и углов из условия
2. Проверяем найденные вертикальные реакции, составляя уравнение проекций всех сил на ось у:
Горизонтальную реакцию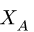
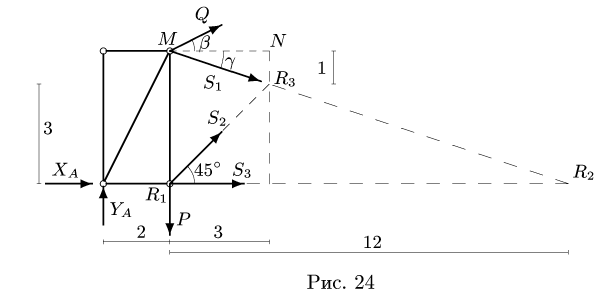
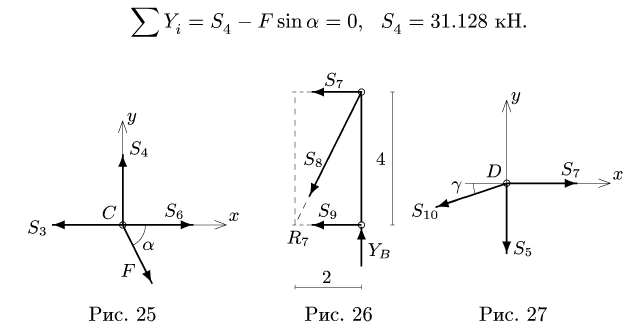
3. Методом Риттера находим усилия в стержнях 1, 2, 3. Сечением I-I (рис. 23) мысленно разделяем ферму на две части, пересекая три стержня.Действие разрезанных частей заменяем их усилиями.
Рассматриваем левую часть (рис. 24), на которую действуют четыре известных силы 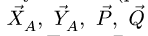
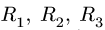
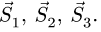
Точка 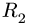
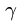
Уравнения метода Риттера имеют вид
Находим решение системы:
4. Методом вырезания узлов определяем 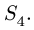
Усилие больше нуля, следовательно, стержень 4 растянут. Усилие в стержне 5 методом Риттера определить нельзя — не существует сечения, делящего ферму на две части и пересекающего при этом три стержня. В этом состоит недостаток метода. Поэтому воспользуемся методом вырезания узлов совместно с методом Риттера. Находим 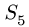
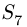
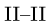
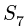
Находим 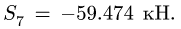
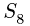
Вырезаем узел D и составляем уравнения равновесия (рис. 27):
Исключая 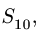
Результаты расчетов в кН занесем в таблицу:
Второе свойство имеет исключения. Существуют фермы, которые одним сечением можно разделить на две, рассекая N > 3 стержней. При этом для одного из стержней существует точка Риттера — точка пересечения остальных N — 1 стержней (подумайте, как выглядит такая ферма).
2. Сечение Риттера не обязательно должно изображаться непрерывной линией. В ферме на рис. 4, с. 15 для определения усилия в стержне АВ надо выполнить разрывное сечение (какое?). Экспериментируя с сечениями, не забывайте про три его основных свойства.
3. Рассматривая одну из частей рассеченной фермы, забудьте на время о существовании другой. Иначе в уравнения равновесия вы можете случайно включить внешние силы или реакции опор отброшенной части.
4. Не стоит беспокоиться, если точка Риттера находится на отрезанной части, располагается где-нибудь далеко или попадает на шарнир. Ее положение может быть где угодно.
5. В уравнения метода Риттера (моментов или проекций) должно войти только одно усилие стержня фермы. В этом основной смысл метода Риттера. Очень часто встречается следующая ошибка. Составляя уравнение, студент неправильно выбирает точку Риттера или составляет не то уравнение, например, уравнение проекций вместо уравнения моментов. При этом в уравнение кроме одного неизвестного усилия входят и другие, ранее найденные. В принципе такое уравнение может быть и верно, и ответ получится верным, но это не метод Риттера, где определение усилий производится независимо одно от другого во избежание накопления ошибок.
6. Положение точки Риттера для каждого стержня не зависит от рассматриваемой части. Однако степень сложности уравнения моментов для разных частей фермы может существенно отличаться. Для большей надежности решения уравнение Риттера (в форме уравнения моментов или уравнения проекций) для одной части может служить проверочным для другой.
7. Проверить расчет можно на компьютере.
Ферма и графический расчет
Постановка задачи:
С помощью диаграммы Максвелла-Кремоны найти усилил в стержнях фермы.
План решения:
Графический метод расчета ферм является дополнением к аналитическим методам расчета, которые вы изучили в предыдущем параграфе. Диаграмма Максвелла-Кремоны состоит из отдельных силовых многоугольников. Каждый многоугольник соответствует равновесию какого-либо узла фермы.
1. Обозначаем усилия в стержнях фермы.
2. Освобождаем ферму от связей. Действие опор заменяем их реакциями. Составляем три уравнения равновесия. Находим реакции.
3. Проверяем найденные реакции, составляя еще одно уравнение равновесия.
4. Изображаем все силы, действующие на ферму (включая найденные аналитически реакции опор), в виде векторов вне фермы. Если реакция опоры отрицательная, то заменяем ее направление на противоположное. Для графического способа требуются только реальные направления реакций.
5. Обозначаем буквами или цифрами внешние поля — области чертежа, разделенные силами и стержнями фермы.
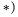
6. Обозначаем буквами или цифрами внутренние поля — области, ограниченные стержнями фермы.
7. Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям.
8. Построение диаграммы Максвелла-Кремоны начинаем с многоугольника внешних сил. Выберем направление обхода фермы (по часовой стрелке или против). Начинаем с произвольной силы. Откладывая ее в масштабе и соблюдая направление, обозначаем на диаграмме начальную и конечную точку строчными буквами, соответствующими ее новому обозначению по направлению обхода. Следующая сила пристраивается к концу первой и т.д. до замыкания многоугольника внешних сил и реакций опор.
9. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены точки двух соседних с ней полей.
Таким образом, начинать графический расчет можно с поля, у которого имеется два соседних с ним внешних поля, уже отмеченные на диаграмме. Искомая точка лежит на пересечении прямых, параллельных стержням, имена которых состоят из имени искомой точки и точек найденных внешних полей. Этот пункт выполняем многократно, до полного построения диаграммы. Модули усилий в стержнях равны длинам соответствующих отрезков на диаграмме.
10. Определяем знаки усилий. Рассматриваем шарнир фермы, к которому подходит какая-либо внешняя нагрузка или стержень с усилием известного знака. Равновесие шарнира изображено на диаграмме замкнутым силовым многоугольником с заданным направлением обхода. Сопоставляя направление усилия на диаграмме и его направление в вырезанном узле, определяем знак усилия. Если направление вектора на многоугольнике совпадает с направлением вектора, приложенного к узлу, то усилие больше нуля. В противном случае — усилие меньше нуля, т.е. стержень сжат.
Задача №11
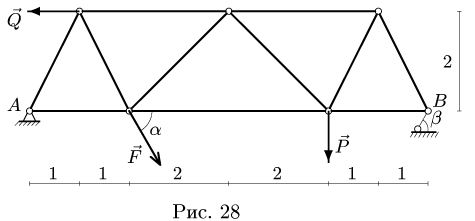
С помощью диаграммы Максвелла-Кремоны найти усилия в стержнях фермы (рис. 28).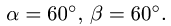
Решение
1. Обозначаем усилия в стержнях фермы так, как это принято в строительной механике. Усилия в стержнях верхнего пояса (слева направо) — 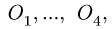
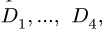
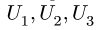
2. Определяем реакции опор фермы. Реакцию 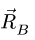
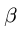
Решаем уравнения и получаем следующие значения:
3. Проверяем вертикальные реакции, составляя уравнение проекций на вертикальную ось:
4. Изображаем все силы, действующие на ферму. Реакцию 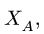
5. Обозначаем внешние поля — области чертежа, разделенные силами и стержнями фермы, — 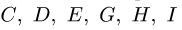
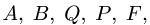
6. Обозначаем внутренние поля 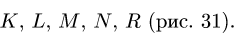
7. Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям. Приведем таблицу соответствия имен.
8. Строим многоугольник внешних сил. Выберем направление обхода фермы по часовой стрелке. Начинаем с произвольной силы, например, F = 20 кН. Откладывая в масштабе эту силу и соблюдая ее направление, обозначаем начальную и конечную точку строчными буквами г и с, соответствующими направлению обхода — из поля I в поле С. Следующая по часовой стрелке нагрузка — вертикальная реакция опоры 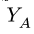
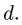
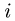
9. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены два соседних с ним поля. Таким образом, начинать графический расчет можно с поля у которого соседние поля Н и G определены на диаграмме, или К с известными соседними полями Е и С (рис. 31). Рассматриваем поле К. По направлению стержней ЕК и КС проводим линии через точки ей с диаграммы. Точка их пересечения — 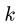
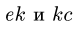
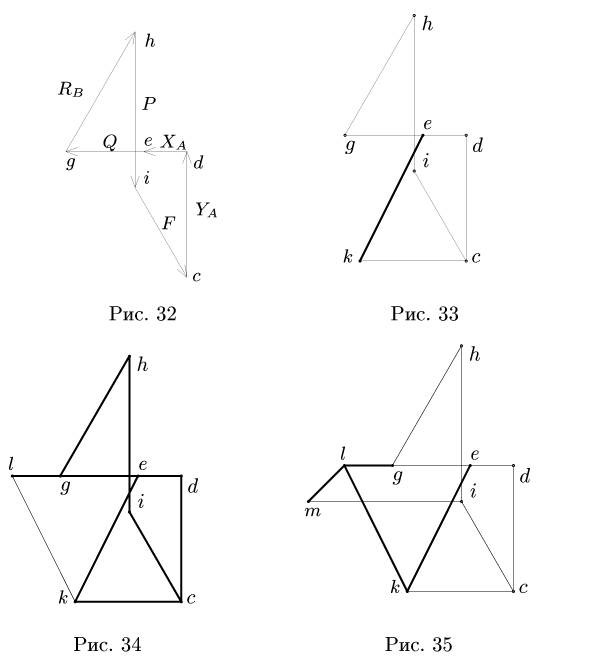
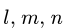
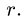
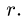
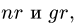
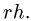
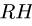
10. Определяем знаки усилий. Рассмотрим, например, усилие Ох. Вырезаем узел А, к которому приложено усилие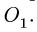
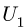
Здесь обход cdek против часовой стрелки задает реакция опоры 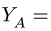
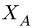
Если направление вектора на многоугольнике совпадает с направлением вектора, приложенного к узлу, то усилие больше нуля — стержень растянут. В противном случае — усилие 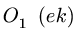
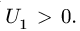
Окончательные результаты в кН заносим в таблицу:
- Замечание 1. Точность, с которой можно получить усилия графическим способом, обычно невысока. Результаты с тремя знаками после запятой, данные в таблицах, получены, конечно, не графически, а из решения задачи аналитическим методом вырезания узлов
.
- Замечание 2. Графический способ расчета ферм в реальной инженерной практике безнадежно устарел, для расчета пространственных ферм он вообще не годится. Однако в учебных целях, для проверки аналитического решения и как пример изящного и быстрого определения усилий с помощью карандаша и линейки, диаграмма Максвелла-Кремоны сохраняет свое значение.
- Замечание 3. В качестве необычной задачи программирования, предлагаем попробовать найти алгоритм автоматического построения диаграммы Максвелла-Кремоны в системе Maple V, Maple 7, Mathematics 4 или в любом другом пакете, позволяющем работать с графикой. Основное требование к программе — не составлять уравнения равновесия узлов фермы в проекциях. Допустимо найти аналитическим методом реакции опор.
Пространственная ферма
Постановка Задачи. Определить усилия е стержнях пространственной фермы, нагруженной в одном узле силами.
План решения:
Задача является естественным обобщением задачи § 1.1, с. 14, в которой методом вырезания узлов определялись усилия в простейшей плоской ферме. Этот же метод применим и здесь, единственное отличие — вместо двух уравнений равновесия узла в проекциях на оси в пространственной задаче будет три уравнения.
1. Узлы фермы находятся в равновесии. Вырезаем узлы, заменяя действие стержней их реакциями. Реакцию незагруженного стержня направляем вдоль его оси. Используя правило знаков, согласно которому усилие растянутого стержня считается положительным, реакцию каждого стержня направляем из шарнира по направлению внешней нормали сечения стержня. Расчет начинаем с узла, к которому подходят три стержня с неизвестными усилиями.
2. Для каждого из шарниров составляем по три уравнения равновесия в проекциях. Решаем полученную систему.
Задача №12
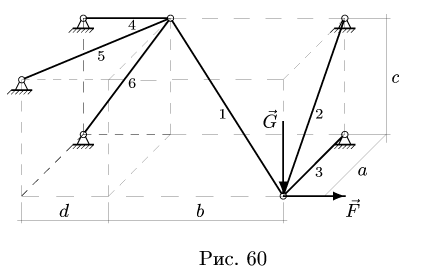
Найти усилия в стержнях 1-6 пространственной фермы, нагруженной в одном узле вертикальной силой G = 100 кН и горизонтальной F = 40 кН. Даны размеры а = 12 м, b = 16 м, с = 10 м, d = 5 м (рис. 60).
Решение
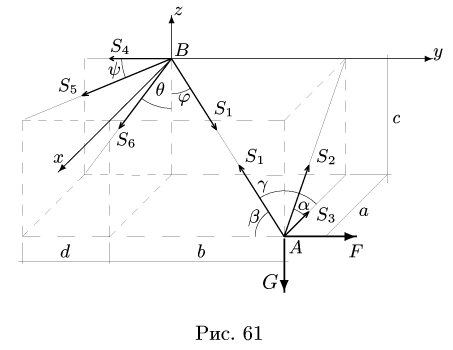
1. Узлы А и В находятся в равновесии. Вырезаем эти узлы, заменяя действие стержней их реакциями, направленными из узла к стержню(рис 61.)
Стержень 1 является общим для обоих узлов, поэтому на рисунке есть два противоположно направленных вектора с усилием 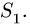
2. Расчет начинаем с узла А, к которому подходят три стержня с неизвестными усилиями. Составляем уравнения равновесия узла в проекциях на три оси координат:
Система уравнений (1) содержит три неизвестных усилия
Вычисляем тригонометрические функции, входящие в уравнения.
Решение системы (1):
Знаки найденных усилий показывают, что стержни 1 и 2 растянуты, а стержень 3 сжат. Составляем уравнения равновесия узла В:
Уравнения (2) содержат три неизвестных усилия 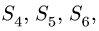
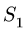
Решение системы (2):
Знаки найденных усилий показывают, что стержни 5 и 6 сжаты, а стержень 4 растянут.
Результаты расчета (в кН) заносим в таблицу:
- Пространственная система сходящихся сил
- Момент силы относительно точки и относительно оси
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Параллельные силы
- Произвольная плоская система сил
- Равновесие системы, состоящей из нескольких тел
- Графостатика в теоретической механике
Содержание:
- Расчет усилий в стержнях фермы
- Простые фермы
- Определение усилий в стержнях фермы
- Определения усилий в стержнях фермы
- Порядок решения задач на тему: Расчет усилий в стержнях фермы
- Способ вырезания узлов
- Способ сечений (метод Риттера)
- Примеры решения задач на тему: Расчет усилий в стержнях фермы
Расчет ферм состоит в определении продольных усилий в стержнях, а также перемещений отдельных узлов. Настоящий параграф посвящен определению усилий в стержнях ферм. Для нахождения внутренних усилий мысленно разрезают ферму на две части и рассматривают условия равновесия одной из частей, к которой прикладывают внешние силы и пока неизвестные усилия в разрезанных стержнях.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Расчет усилий в стержнях фермы
Фермой называется конструкция, состоящая из стержней, соединённых между собой шарнирами, которые называются узлами фермы. Внешняя нагрузка на ферму передаётся через эти узлы. Каждый стержень в ферме находится в условиях простого осевого растяжения – сжатия, но общая деформация фермы – изгибная, то есть ферма работает на изгиб.
Простые фермы
Фермой называется геометрически неизменная конструкция, состоящая из стержней, соединенных между собой на концах шарнирами (рис.6.1).
Шарниры, соединяющие стержни между собой, называются узлами фермы. Стержни, расположенные внутри контура фермы, образуют ее решетку. Если все стержни, образующие ферму, расположены в одной плоскости, то такая ферма называется плоской.
При расчете ферм принимается, что весом стержней можно пренебречь и шарниры расположены на концах стержней. Поскольку нагрузки, действующие на ферму, передаются в шарнирах, то каждый стержень будет воспринимать усилие, которое направлено вдоль оси стержня, то есть будет либо растянут или сжат.
Среди разнообразных типов ферм различают два основных вида:
1. фермы без лишних стержней.
2. фермы, в которых есть лишние стержни.
В дальнейшем будем рассматривать простые плоские фермы, которые строятся следующим образом: к основному стержневому треугольнику двумя стержнями присоединяется новый шарнир (узел), к него второй и т.д.
По своему назначению фермы подразделяются в основном на мостовые, стропильные и крановые (рис.6.1 а, б, в).
Зависимость между числом стержней 

Если 

При расчете ферм предполагается, что выполняются следующие условия:
1. все стержни фермы — прямолинейные.
2. трение в шарнирах отсутствует.
3. силы, действующие на ферму, лежат в плоскости этой фермы и приложены только к ее узлам.
4. собственный вес каждого стержня фермы настолько мал по сравнению с силами приложенными к узлам фермы, что им можно пренебречь.
Основной задачей расчета простых ферм является определение усилий в стержнях фермы, которые представляют собой внутренние силы, возникающие в стержнях под действием внешних сил.
Определение усилий в стержнях фермы
Ограничимся двумя аналитическими способами определения усилий в стержнях простых ферм:
1. способ вырезания узлов.
2. способ сечений (метод Риттера).
Способ вырезания узлов состоит в том, что каждый узел вырезают из фермы и рассматривают отдельно в равновесии под действием приложенных к нему внешних сил и усилий разрезанных стержней.
Метод Риттера позволяет определить усилия в любом стержне фермы независимо от усилий в других стержнях и заключается в том, что ферма рассекается на две части таким образом, чтобы в сечении было не более трех стержней с неизвестными усилиями.
Определения усилий в стержнях фермы
Определение усилий в стержнях ферм упрощается, если при рассмотрении равновесия узла встречаются следующие случаи.
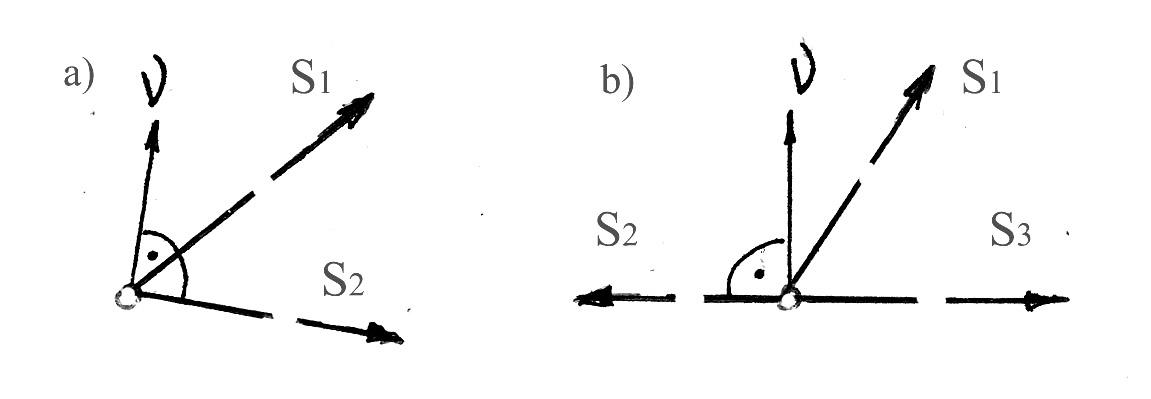
1. Узел фермы с двумя стержнями без нагрузка (рис.6.2).
В этом случае усилия в каждом из стержней равны нулю, поскольку иначе равновесие узла было бы невозможно.
2. Узел фермы с двумя стержнями, по оси одного из которых приложена сила 
Реакция стержня, с осью которого совпадает направление силы, по модулю равна, а по направлению противоположна силе 
3. Узел фермы с тремя стержнями, оси двух стержней которого направлены вдоль прямой (рис.6.4).
В этом случае усилие в третьем стержне равно нулю, а в каждом из первых двух или тоже равны нулю, либо равны между собой по величине и направлены в противоположные стороны, то есть эти стержни либо не подвергаются нагрузкам, либо оба сжаты (растянуты) с одинаковыми силами.
4. Узел фермы с тремя стержнями, у которого оси двух стержней направлены вдоль одной прямой, а по направлению оси третьего стержня приложена сила 
В этом случае реакция третьего стержня по величине равна, а по направлению противоположна силе 
5. К узлу фермы с тремя стержнями с осью одного из стержней приложена сила 
В этом случае реакция стержня, ось которого совпадает с линией действия силы 

6. Узел фермы с четырьмя стержнями, в которой оси стержней попарно расположены по одной прямой (рис.6.7).
В этом случае усилия или:
а) равны нулю в каждом стержне;
б) равны нулю только в двух стержнях, что расположены по одной прямой, а в двух других равны по модулю и противоположны по направлению;
в) для каждой пары стержней, что расположены по одной прямой, равны между собой по модулю и противоположны по направлению.
Порядок решения задач на тему: Расчет усилий в стержнях фермы
Существует два способа:
Способ вырезания узлов
1. Выделить ферму, равновесие которой надо рассмотреть для нахождения неизвестных величин.
2. Приложить активные силы, действующие на объект равновесия.
3. Отбросить связи и заменить их действие реакциями.
4. Рассмотреть равновесие фермы, как твердого тела, под действием активных сил и реакций связей.
5. Определить реакции опор.
6. Вырезать узел, к которому сходятся два стержня и рассмотреть его равновесие под действием активных сил и реакций разрезанных стержней. (При выборе направления реакции стержня, лучше принимать что он растянут, то есть направлять реакцию от узла стержня).
7. Пользуясь условиями равновесия плоской системы сходящихся сил, определить реакции разрезанных стержней.
8. Двигаясь по ферме от узла к узлу, аналогично рассматривается равновесие каждого узла. При этом, в каждом последующем вырезанном узле должно быть только два стержня, реакции в которых неизвестны.
Способ сечений (метод Риттера)
1. Определить опорные реакции, рассматривая равновесие фермы как твердого тела, находящегося под действием плоской системы сил.
2. Мысленно разрезать ферму, к которой приложены все внешние силы, на две части таким образом, чтобы число разрезанных стержней не было больше трех.
3. Отбросить одну из частей фермы и заменить ее действие реакциями разрезанных стержней. (Рекомендуется принимать, что все стержни растянуты).
4. Рассмотреть равновесие выбранной части фермы под действием активных сил и реакций разрезанных стержней. (При составлении условий равновесия лучше руководствоваться тем, чтобы в каждое уравнение входила одна неизвестная реакция. Для этого, за центр моментов выбирают точку, где пересекаются линии действия двух неизвестных реакций, а в случае, когда два разрезанных стержня параллельны, составляют уравнение проекций на ось, которая перпендикулярна этим стержням).
5. Решить составленную систему уравнений, определить неизвестные усилия в стержнях.
Примеры решения задач на тему: Расчет усилий в стержнях фермы
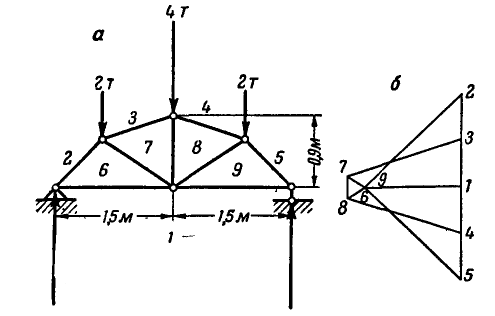
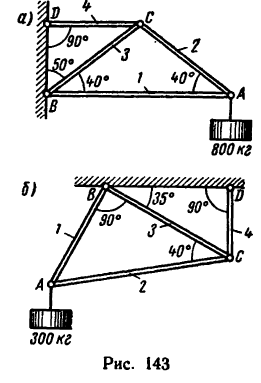
Ферма (рис.6.8) нагружена вертикальными силами 



Определить опорные реакции и усилия в стержнях, если
Решим задачу первым способом – методом вырезания узлов.
Для определения опорных реакций рассмотрим равновесие фермы в целом.
На ферму действуют активные силы 





Свяжем с фермой систему координат 




Реакция 





Составим уравнения равновесия для системы сил, действующей на ферму:
где
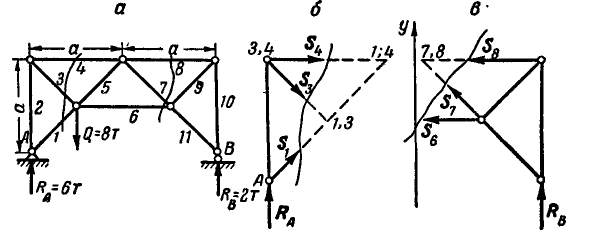
Из второго уравнения получим 
Из первого уравнения найдем 
После определения реакций опор перейдем к определению усилий в стержнях. Для этого надо рассмотреть равновесие каждого узла фермы в отдельности, мнимо отбросив все сходящиеся к нему стержни и заменив их действие на узел реакциями.
Первыми надо рассматривать узлы, к которым приложены только две неведомые силы. В данной задаче таким требованиям соответствуют два узла 

Начнем с узла 





Реакции стержней направим от узла, предполагая, что стержни растянуты.
Через точку 


Решив последовательно уравнения (4) и (3), получим:
Отрицательное значение реакции 
Следующим рассмотрим узел 






Узел 






Проведем через точку 
Из уравнения (5) выразим 
Подставим выражение для 

Тогда:
Таким образом, стержень 6 растянут, как и предполагалось, а стержень 4 – сжат.
Следующим вырезаем узел 
К узлу приложены две неизвестные реакции 







Проводим через точку 

Из уравнения (8) найдем
Из уравнения (7) находим 
Таким образом, стержень 2 растянут, а стержень 7 – сжат.
Рассмотрим равновесие узла 
На узел действуют неизвестна реакция 







Через точку 




Отсюда:
Стержень 3 — сжатый.
Таким образом определены усилия во всех стержнях фермы. Выяснено, что стержни 1, 2, 6 – растянуты, а стержни 3, 4, 5 и 7 – сжаты.
Рассмотрение равновесия узла 
Уравнения равновесия для узла 
Подставив в эти уравнения числовые данные, получим:
Уравнения (10) и (11) преобразуются в тождества, что указывает на правильность выполненного расчета.
Проверим, насколько верно определены усилия в отдельных стержнях фермы методом сечений (методом Риттера).
Для определения усилий в стержнях 1, 6, 4 рассечем ферму сечением 




Таким образом, левая часть фермы будет находиться в равновесии под действием реакции опоры 




Составим уравнения равновесия для левой части фермы.
Воспользуемся формой условий равновесия в виде 3-х уравнений моментов для произвольной плоской системы сил.
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно трех произвольных центров, которые не лежат на одной прямой, были равны нулю:
Выберем за центры моментов точки:









Из уравнения (12) определим реакцию 
где 






Из уравнения (13) определим:
где 









Из уравнения (14) найдем:
где 






Таким образом, при определении усилий в стержнях фермы методом сечений, имеем 
Ответ: 


Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Расчет фермы, как и всякой статически
определимой системы начинается с
определения опорных реакций, Это делают
обычным способом как в балке, составляя
уравнения равновесия для фермы в целом.
После этого приступают к определению
усилий в стержнях.
Основной метод состоит в отделении
части фермы и рассмотрения ее равновесия.
Этот метод разрезовприменялся и в
решении задач сопротивления материалов.
Последовательность действий была
определена еще в курсе теоретической
механики, когда изучалась статика
системы сил на плоскости.
1.Проводят мысленно разрез фермы, который
должен проходить, вообще говоря, не
более, чем через три стержня, в том числе
и через тот, усилие в котором следует
определить.
2. Отбрасывают левую или правую часть
фермы относительно разреза (удобнее
отбрасывать ту часть, к которой приложено
большая часть нагрузок).ли вырезается
узел, то он просто изывается из фермы.
3. Заменяют действие отброшенной части
продольными усилиями в разрезанных
стержнях, полагая их все растягивающими
( действующими “от узла”).
4. Составляют уравнение равновесия так,
чтобы искомое усилие входило в него как
единственное неизвестное.
5. Решают уравнение, находят усилие. Если
результат получается со знаком плюс,
то стержень растянут, если минус – сжат.
Итак, метод общий – метод разрезов. Но
при составлении уравнения равновесия
нужно применить такой способ, Который
позволяет избежать решения системы
совместных уравнений. Различают несколько
таких способов: способ моментной точки,
способ проекций и способ вырезания
узлов.
В строительной механике часто применяют
“фирменные” обозначения усилий в
стержнях. Буквой О обозначают усилие в
элементах верхнего пояса, U– в элементах нижнего пояса,D– в раскосах,V- в стойках.
Этим буквам придается два индекса,
соответствующих номерам узлов по концам
стержня. Некоторые из этих букв оказываются
“перегруженными содержанием”. Например,
буквойVобозначают
вертикальную составляющую опорной
реакции и работу внешних сил. Поэтому
усилия в стержнях фермы можно обозначать
одной буквой (обычноS) с
двумя индексами.
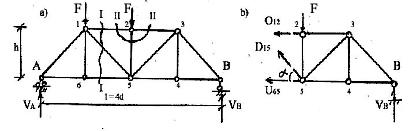
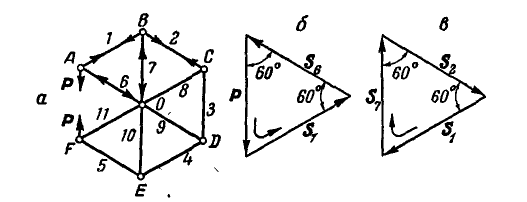
Определим усилия в стержнях фермы,
показанной на рис.4.2.
Опорные реакции определим как в балке
с пролетом, равным пролету фермы:
-VB
VB
=
Рис.4.2
Найдем усилие O12
.Проведем сечениеI–I(рис.4.2 а).
Отбросим левую часть фермы. и заменим
Рис.4.2
ее действие на оставшуюся правую часть
неизвестными усилиями О12 ,D15
иU65 , полагая
их растягивающими (рис.4.2.b).
Уравнение равновесия нужно составить
так , чтобы в него вошло усилие О12
и не вошлиD15 иU65 . Для этого следует
взять момент всех сил, приложенных к
правой части фермы, относительно точки
5, играющей в данном случае роль моментной
точки.
Таким образом, для определения усилия
О12примененспособ моментной
точки.
За моментную принимают ту точку, в
которой пересекаются все неинтересующие
нас стержни , попавшие в сечение..Следовательно, в разрез могут попасть
иn стержней, если
n-1 пересекаются
в одной точке. (рис. 4.3).
Найдем усилие в раскосеD15.
Проводим то же сечение I–I. Изложенный выше
способ здесь не применим: моментную
точку придется
Рис.4.3
искать на пересечении стержней О12 иU65 , а они параллельны.
Поэтому составляем уравнение другого
вида: проектируем все силы, приложенные
к правой части фермы, на вертикаль,
применяяспособ проекций:
Найдем усилие V25.
Провести разрез фермы на две части так,
чтобы он прошел через стойку 2-5 и еще
через два стержня не удается. Поэтому
проводят сечение II–II,
применяяспособ вырезания узлов(рис.4.4).
Проектируя все силы на вертикаль,
получаем
Рис.4.4
Применяя способ вырезания узлов, нужно
помнить, что для системы сходящихся сил
можно записать только два уравнения
равновесия. Поэтому в вырезаемом узле
не должно быть более двух стержней с
неизвестными усилиями.
До начала определения усилий в элементах
фермы полезно выявить те стержни, усилия
в которых при заданной нагрузке равны
нулю. Такие стержни называют нулевыми.
Правила определения нулевых стержней
следуют из уравнений равновесия.
Если в узле сходится два стержня и
узел не нагружен, то усилия в обоих
стержнях равны нулю (рис.4.5a).
Проектируя силы на направление,
получаем
S1= 0. После этого
из проекции на направлениеS2Рис.4.5
следует, что и S2=
0.
Если в узде сходятся три стержня , два
из которых лежат на одной прямой и узел
не нагружен (рис.4.5b), то
усилие в ответвляющемся стержне равно
нулю (S1 = 0), а два
других равны между собой (S2=S3 ). Первое заключение
следует из уравнения равновесия,
втрое – получаем, проектируя все силы
на прямую, вдоль которой действуют силыS2 иS3
.
Пользуясь этими правилами легко
установить, что все стержни, перечеркнутые
одной чертой в ферме на рис.4.6, нулевые.
Рис.4.6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи по определению усилий в двух стержнях, скрепленных шарнирно между собой и с вертикальной опорной стеной, в точке соединения которых подвешен груз.
Задача
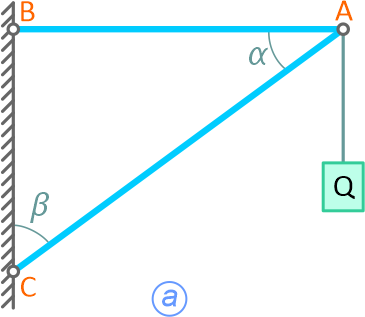
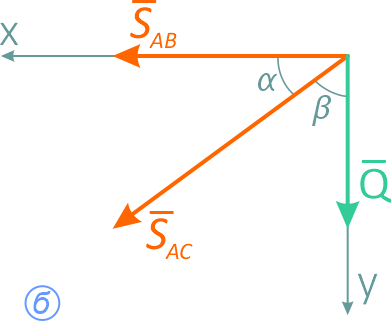
Груз Q=1000Н удерживается с помощью двух невесомых стержней, шарнирно скрепленных между собой в точке A и в шарнирах B и C с вертикальной стеной (α=60°, β=30°).
Рисунок 2.1
Определить усилия в стержнях AB и BC (рисунок 2.1,а).
Другие примеры решений >
Помощь с решением задач >
Решение
Короткое видео про реакции в разных типах связей:
Другие видео
В данном случае следует рассмотреть равновесие точки A, т.к. все силы приложены в этой точке.
Нить с грузом натянута силой Q. В равновесии точку A удерживают два невесомых стержня. Их реакции всегда направлены вдоль стержней.
Реакции принято направлять от узла (точки A), т.е. предполагается, что стержни работают на растяжение (рисунок 2.1, б). В случае отрицательного ответа при решении уравнений стержень работает на сжатие.
При равновесии системы сил выполняется равенство
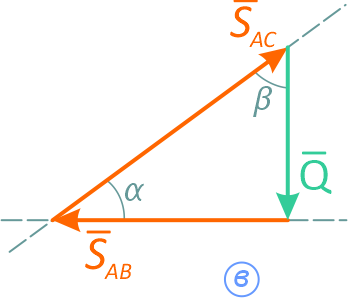
Это векторное равенство можно построить. Откладываем в масштабе известную силу Q, к концу вектора прибавляем SAB, т.к. его величина и направление неизвестны, проводим через конец вектора Q горизонтальную линию (параллельно SAB, рисунок 2.1, б).
Замыкающий вектор SAC должен пройти через начало вектора Q под углом β к вертикали. Результатом построения является замкнутый треугольник (рисунок 2.1, в). Величины усилий в стержнях можно получить, умножая замеренные значения векторов сил на масштаб или воспользовавшись теоремой синусов:
Направление силы SAC в силовом треугольнике говорит о том, что этот стержень работает на сжатие.
Задача может быть решена и аналитически. Для этого выбираем систему координат xAy (рисунок 2.1, б) и проецируем на ее оси векторное равенство (2.3):
При этом
После решения уравнений равновесия находим
То есть и в этом решении по знакам в ответах получаем, что стержень AC работает на сжатие, а стержень AB – на растяжение.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Марина Анатолиевна Придатко
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Ферма в строительной механике
Ферма – это стержневая система, относящаяся к геометрически неизменяемым конструкциям после замены жестких ее узлов на шарнирные.
Следует заметить, что в стержнях любой фермы при отсутствии расцентровки могут возникать только растягивающие или сжимающие усилия. Фермы, полученные из прямолинейных стержней, которые соединены между собой в узлах, образуют геометрически неизменяемую систему, к которой можно прикладывать нагрузку только в узлах.
Также к фермам с некоторыми оговорками следует относить шпренгельные балки, которые представляют собой комбинацию двух- либо трехпролетной неразрезной балки с подпружной тягой. Такие балки часто применяются в стальных и деревянных каркасах с верхними поясами из неразрезных прокатных профилей.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Расчет ферм
Расчет фермы заключается в определении ее опорных реакций. Опорные реакции фермы определяются по аналогии с простыми балками, работающими на изгиб.
Что касается определения усилий в стержнях фермы, то для этого существует несколько способов:
-
Способ моментной точки. Данный метод должен применяться, если ферма рассекается на две части таким образом, что в разрез попадает лишь три ее стержневых элемента. Для определения усилия в одном из них следует найти точку пересечения двух других стержней (ее называют моментной точкой), после чего записать уравнение равновесия для отсеченной части фермы (сумма моментов всех сил системы относительно данной точки);
-
Способ проекций. Данный метод применяется в случае, когда в разрез фермы также попадает лишь три стержня. При определении усилий в одном из стержней два других оказываются параллельны (следовательно, моментная точка удаляется в бесконечность). В данном случае записывается уравнение проекций сил на вертикальную ось любой отсеченной части. Способ проекций чаще всего применяется для определения усилий в раскосах или стойках ферм с параллельными поясами;
-
Способ вырезания узлов. Данный способ применяется в случаях, когда два вышеизложенных метода неприменимы (нельзя рассечь ферму через три стержня). Метод заключается в отделении узла, к которому принадлежит интересуемый стержень и рассмотрения его равновесия.
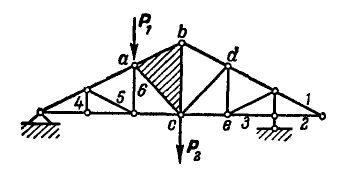
«Как определить усилие в отмеченном стержне фермы» 👇
Метод вырезания узлов
Метод вырезания узлов является наиболее универсальным методом расчета. Как уже отмечалось выше, вначале для расчета требуется вырезать узел, в котором пересекается не более двух стержней с неизвестными внутренними усилиями. Далее, последовательно вырезать узлы до достижения интересуемого стержня. Следует заметить, что в каждом последующем вырезаемом узле также должно быть не более двух неизвестных усилий.
Главный недостаток метода вырезания узлов заключается в том, что ошибка, допущенная при определении усилия в одном стержне, влияет на результат дальнейшего расчета.
Замечание 1
Фермы, в которых каждый из узлов добавляется к предыдущему с помощью двух стержней, не лежащих на одной прямой, называются простейшими.
Как уже отмечалось выше, реакции опор любой фермы определяются как для простой однопролетной балки с помощью составления уравнений равновесия.
Помимо простейших ферм существует системы с более сложными геометрическими характеристиками. Такие фермы называют сложными.
Для определения усилий в сложных фермах применяется метод замены стержней. Путем замены некоторых стержней ферма превращается в простую, которая и закладывается в основу последующего расчета. Систему, полученную в результате такого преобразования, называют заменяющей.
Последовательность действий для определения усилий в заменяющем стержне:
- удаляется какой-либо стержень фермы;
- последовательно удаляются те узлы фермы, которые присоединяются двумя стержнями (такое отбрасывание стержней не влияет на неизменяемость оставшейся части);
- отбрасывание узлов производится до тех пор, пока не обнаружится стержень, имеющий достаточное количество связей с оставшейся системой (стержень, необходимый для его закрепления и будет заменяющим);
- если полученная ферма не будет являться простейшей, то из такой фермы следует удалить еще один стержень и повторить вышеизложенные действия.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

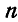
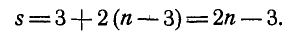
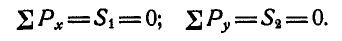
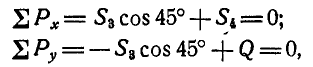
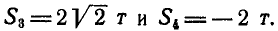
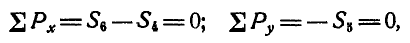
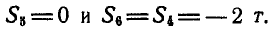

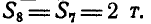
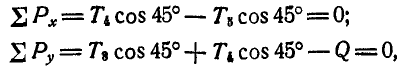
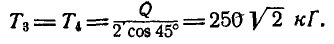
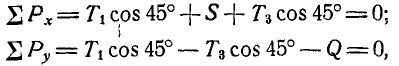
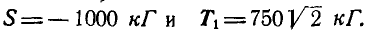
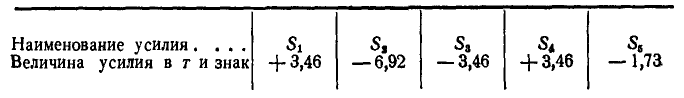
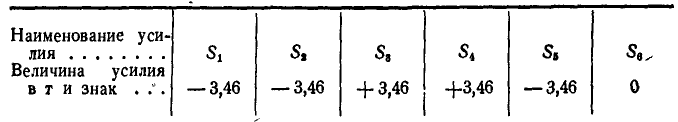
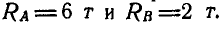
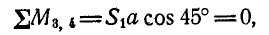
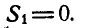
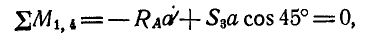
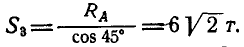
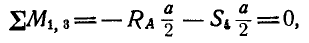
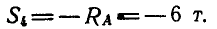
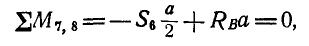
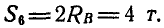

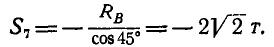
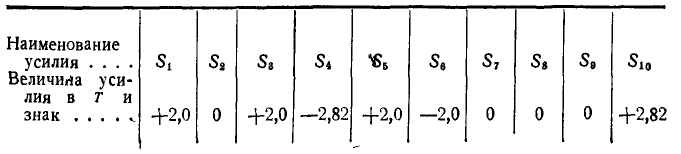
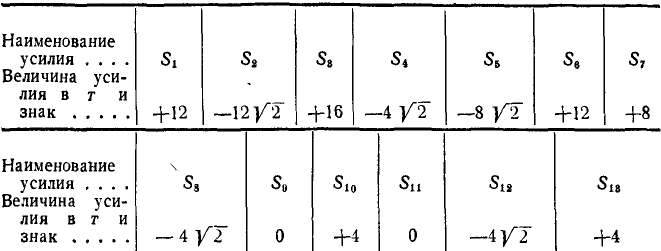
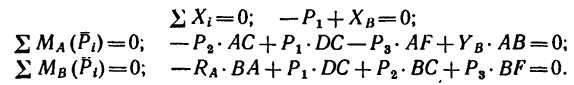
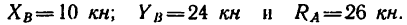
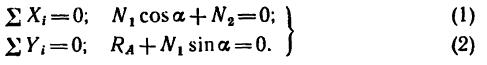
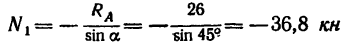
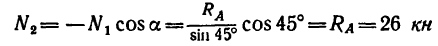
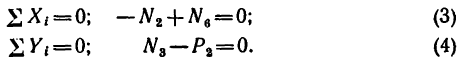
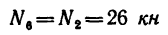
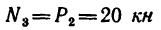
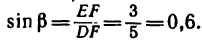
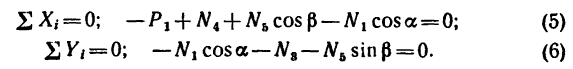
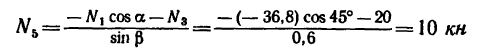
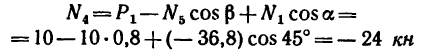
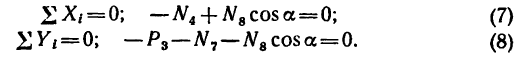
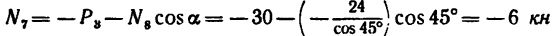
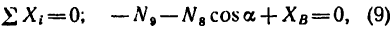
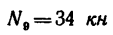

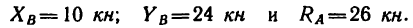
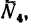
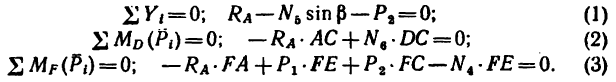
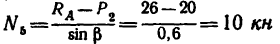
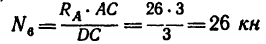
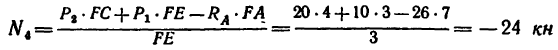
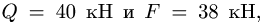
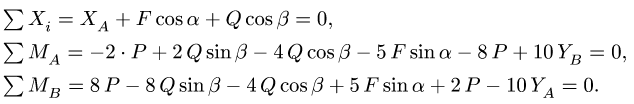
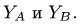
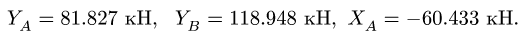
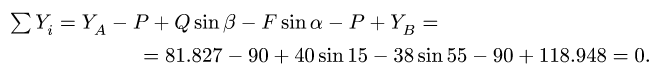
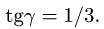
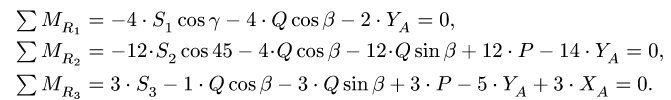
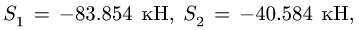
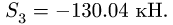
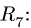
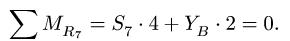
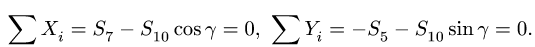
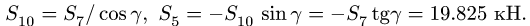

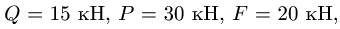
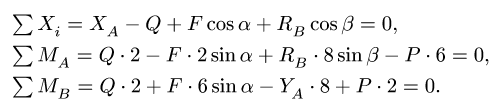
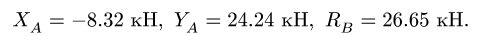
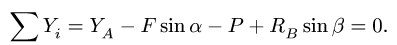
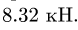


 .
.