Стальные канаты
(ГОСТ 3241-80) используют в механизмах,
полиспастах, различных монтажных
приспособлениях, а также для изготовления
стропов.
Наибольшее
допускаемое усилие в канате определяют
из выражения
S
= P/k,
где Р – разрывное
усилие канта, гарантированное паспортом
(или взятое по ГОСТу для данного типа
каната); k
–коэффициент запаса прочности,
принимаемый в зависимости от условий
работы каната.
в чалочных канатах
различных грузов массой:
до 50 т……………………………………………8
свыше 50
т……………….………………………6
в расчалках, оттяжки
мачт и опор……………3,5
в канатах
подьемно-транспортных устройств при
режиме работы:
ручном………………………………………….4,5
машинном
легком………………..……….…….5
машинном
среднем…………………..……….5,5
машинном тяжелом
и весьма тяжелом.
непрерывного
действия………………..…….…6
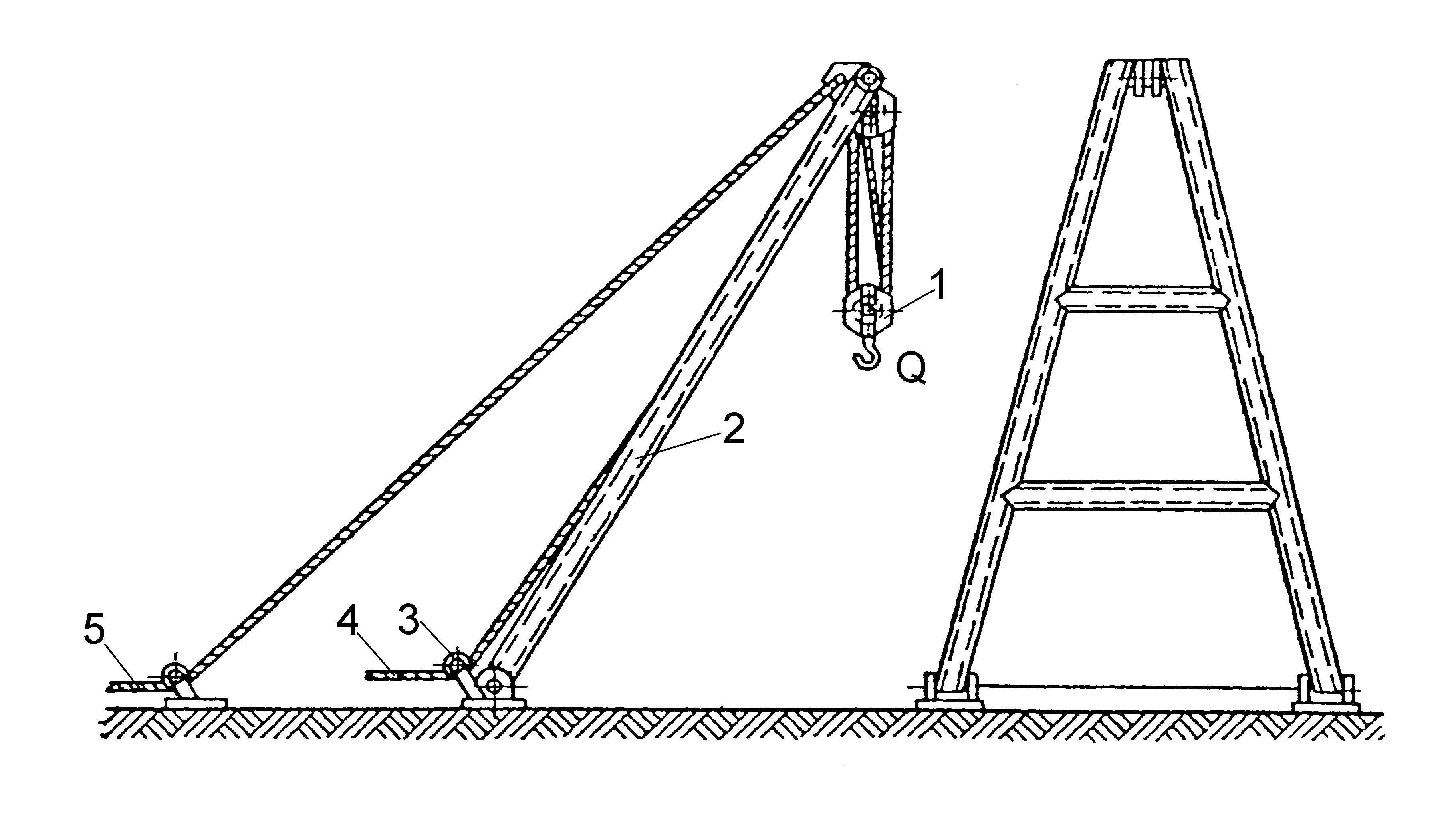
Рис. 122. Шевр: 1 –
грузовой полиспаст; 2 – рама; 3 – отводной
блок; 4 – сбегающая к лебедке ветвь
грузового поли спаста; 5 – канат для
изменения вылета шевра
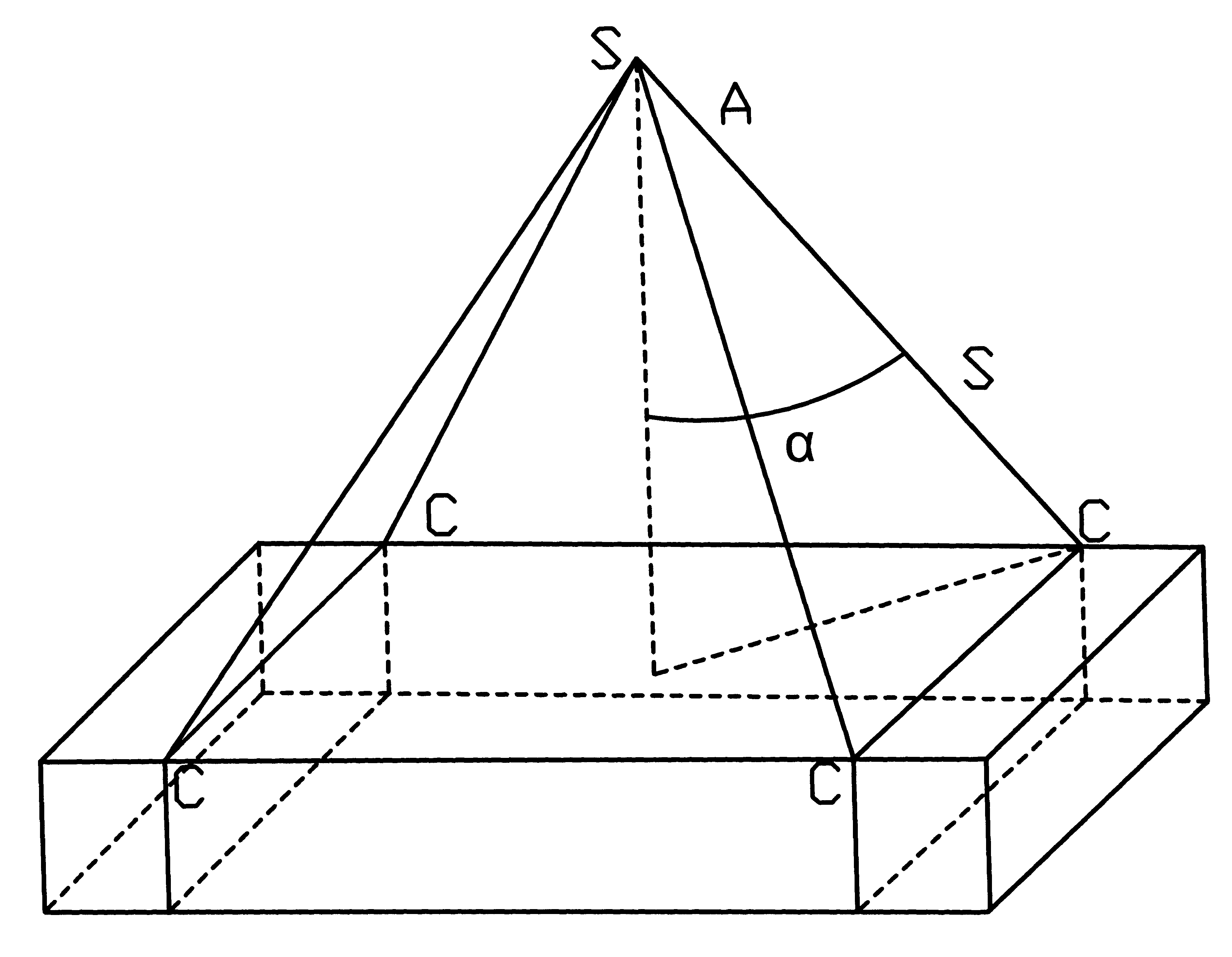
Рис. 123. Схема
расчета натяжения в ветви чалочного
каната
При подвеске
груза к крюку с помощью нескольких
ветвей чалочного каната (рис. 123) натяжение
в каждой ветви определяется из выражения
,
(44)
где Q
– вес груза; m
– число ветвей; α – угол наклона ветвей
к вертикали; kН
– коэффициент
неравномерности нагрузки на ветви
стропа.
Если груз подвешен
на двух ветвях, то kН
= 1. При числе
ветвей больше двух kН
= 1,3 –1,4; для
устойчивого равновесия груза угол α не
должен превышать 60º.
При такелажных
работах применяют также пластинчатые
и сварные цепи. Их используют в качестве
строп или захватных приспособлений.
Цепи рассчитывают аналогично стальным
канатам с коэффициентом запаса прочности
в зависимости от условий работы от 3 до
8.
При расчете
применяется следующий коэффициент
запаса прочности каната: для грузовых
канатов к электролебедкам k
≥ 5, к ручным лебедкам k
≥ 4; для стропов и чалочных канатов k
≥ 6; для расчалок постоянно действующих
кранов k
≥ 3,5. а для кранов и мачт со сроком работы
до 1 года k
≥ 3,0.
Расчет на прочность стропов и чалочных канатов
Представим себе,
что какой-либо груз подвешен на одном
или нескольких параллельных вертикальных
канатах. Канаты будут расположены почти
вертикально в том случае, когда поперечные
размеры груза не велики, а длина канатов
значительна. При этом канаты будут
подвергаться как растягивающим, так и
изгибающим напряжениям; последние
возникают из-за огибания канатом груза
и его перегиба на углах.
Напряжения
растяжения в канате не изменяются по
величине и определяются массой груза
и числом ветвей стропа. Изгибающие же
напряжения зависят от формы груза,
величины углов, огибаемых канатом;
подсчет их величины затруднителен. Для
простоты расчета стропы и чалочные
канаты рассчитывают только на растяжение;
для учета дополнительных напряжений
от изгиба принимают при расчете повышенный
коэффициент запаса прочности, равный
6.
При более значительных
поперечных размерах груза и уменьшении
высоты подвешивания груза направление
ветвей стропа начинает значительно
отклонятся от вертикали, как это видно
на схеме. Угол α означает отклонение
направления ветви стропа от вертикали.
Чем больше отклонится строп от вертикали,
т.е. чем больше угол α, тем большему
растягивающему усилию будут подвергаться
ветви стропа при одной и той же величине
груза.
Таким образом,
усилие, которому подвергается ветвь
стропа, а следовательно, и диаметр каната
стропа зависят от массы поднимаемого
груза, числа ветвей стропа и угла наклона
их к вертикали.
Формула для расчета
усилия на одну ветвь стропа имеет
следующий вид:
,
(45)
где S
– усилие на одну ветвь стропа, кгс; Q
– масса груза, кг; m
– число ветвей стропа; n
– коэффициент, зависящий от угла α
отклонения стропа по вертикали.
Угол α принимается
равным 0, 15, 30, 45; Коэффициент n
равен 1,00, 1,03, 1,15, 1,42.
Угол α более 45º
следует изгибать из-за резкого возрастания
усилия на строп.
Подсчитав усилие,
действующее на одну ветвь стропа,
умножают его на коэффициент запаса
прочности и получают разрывное усилие,
которое должен иметь канат, выбираемый
для изготовления стропа. Затем по
сертификату или из таблиц ГОСТа подбирают
канат с разрывным усилием, равным или
ближайшим большим к полученному по
расчету.
Для тяжелых грузов,
когда диаметр каната стропа из двух
ветвей по расчету получается очень
большим или канат требуемого по расчету
диаметра отсутствует, может быть применен
канат с двойным или большим (4, 6 и 
ветвей и производится пересчет стропа
на большее число ветвей.
Пример.
Требуется определить диаметр каната
стропа для подъема груза массой 5200 кг
при угле отклонения ветвей стропа от
вертикали α = 45º. Выбираем число ветвей
стропа m
= 2. Для α = 45º находим коэффициент n
= 1,42. Тогда усилие, действующее на одну
ветвь стропа S,
будет равно
.
Необходимое
разрывное усилие ветви стропа,
изготовленного из стального каната,
должно быть не менее
,
где k
– коэффициент запаса прочности для
стропов, k
= 6. Тогда разрывное усилие ветви стропа
будет равно
.
Таблица 49
Канаты двойной
свивки типа ЛК-РО конструкции 6x36
(1+7+7/7+14)+1, органический сердечник (ГОСТ
7668-80)
|
Диаметр, мм |
Расчетная масса 100 м смазанного каната, кг |
Маркировочная группа по временному сопротивлению разрыву, кгс/мм2 |
||||||||
|
К |
Проволоки |
140 |
160 |
180 |
200 |
|||||
|
центральной |
1-го слоя |
2-го слоя |
3-го слоя (наружного) |
Расчетное разрывное усилие каната в целом, кгс, не менее |
||||||
|
6 проволок |
42 проволоки |
42 проволоки |
42 проволоки |
84 проволоки |
||||||
|
15,0 |
0,90 |
0,65 |
0,65 |
0,50 |
0,85 |
86,5 |
— |
11450 |
12900 |
13850 |
|
18,0 |
1,1 |
0,8 |
0,8 |
0,6 |
1,0 |
124,5 |
— |
16500 |
17950 |
19450 |
|
20,0 |
1,2 |
0,9 |
0,9 |
0,65 |
1,1 |
152,0 |
— |
2020 |
21950 |
23950 |
|
22,0 |
1,3 |
1,0 |
1,0 |
0,7 |
1,2 |
183,0 |
21200 |
24250 |
26400 |
28650 |
|
23,0 |
1,40 |
1,05 |
1,05 |
0,8 |
1,3 |
212,0 |
24600 |
28150 |
30600 |
33250 |
|
25,5 |
1,60 |
1,15 |
1,15 |
0,85 |
1,4 |
249,5 |
28900 |
33100 |
36000 |
39100 |
|
27,0 |
1,70 |
1,2 |
1,2 |
0,9 |
1,5 |
280,0 |
32500 |
37200 |
40500 |
43950 |
|
29,0 |
1,80 |
1,3 |
1,3 |
0,95 |
1,6 |
321,5 |
37350 |
42650 |
46400 |
50400 |
|
31,0 |
1,90 |
1,4 |
1,4 |
1,0 |
1,7 |
365,5 |
42450 |
48500 |
52800 |
57300 |
Примечание. Канаты,
разрывное усилие которых указано справа
от жирной линии, изготовляются только
из светлой проволоки.
По табл. 49 выбираем
для стропа канат по ГОСТ 7668-69 диаметром
22,0 мм с расчетным пределом прочности
проволоки 160 кгс/мм2,
имеющий разрывное усилие 24250 кгс. Если
выбрать число ветвей стропа m
= 4, то получим усилие на одну ветвь
стропа:
.
Канат стропа должен
в этом случае иметь разрывное усилие.
.
По таблице этому
соответствует канат Ø 15 мм с расчетным
пределом прочности проволоки 160 кгс/мм2,
имеющей разрывное усилие 11450 кгс, т.е.
ближайшее большее к требуемому по
расчету разрывному усилию 11100 кгс.
Вместо расчета
для выбора диаметра стропа можно
пользоваться данными табл. 50.
Таблица 50
Выбор диаметра
стропа
|
Масса
подни-маемого |
|
2 ветви каната |
4 ветви каната |
||||||
|
Количество ветвей |
Угол α, град |
Угол α, град |
|||||||
|
1 |
2 |
3 |
15 |
30 |
45 |
15 |
30 |
45 |
|
|
Диаметр каната |
|||||||||
|
1 |
13,5 |
8,5 |
8,5 |
8,5 |
9,0 |
11,5 |
8,5 |
8,5 |
8,5 |
|
2 |
15,5 |
13,5 |
8,5 |
13,5 |
13,5 |
15,5 |
8,5 |
9,0 |
11,0 |
|
3 |
22,5 |
15,5 |
11,5 |
15,5 |
15,5 |
18,0 |
11,5 |
11,5 |
13,5 |
|
4 |
27 |
18 |
13,5 |
18 |
18 |
20 |
13,5 |
13,5 |
15,5 |
|
5 |
— |
20 |
13,5 |
20 |
20 |
22,5 |
13,5 |
15,5 |
15,5 |
|
6 |
— |
22,5 |
15,5 |
20 |
22,5 |
24,5 |
15,5 |
15,5 |
18 |
|
7 |
— |
22,5 |
15,5 |
22,5 |
24,5 |
27 |
15,5 |
18 |
20 |
|
8 |
— |
— |
18 |
— |
— |
— |
18 |
18 |
20 |
|
9 |
— |
— |
18 |
— |
— |
— |
18 |
20 |
22,5 |
|
10 |
— |
— |
20 |
— |
— |
— |
20 |
20 |
22,5 |
|
12 |
— |
— |
20 |
— |
— |
— |
20 |
22,5 |
24,5 |
|
15 |
— |
— |
22,5 |
— |
— |
— |
24,5 |
24,5 |
27 |
|
20 |
— |
— |
29 |
— |
— |
— |
27 |
29 |
33,5 |
|
25 |
— |
— |
33,5 |
— |
— |
— |
29 |
33,5 |
36,5 |
Примечание. Таблица
составлена для стальных канатов с
пределом прочности проволоки 160 кгс/мм2
(ГОСТ 3071-74) при запасе прочности, равном
6.
Расчет диаметра
каната необходимо производить по
исходным данным (табл. 51). Полученные
результаты занести в таблицу.
Таблица 51
Варианты расчета
|
Номер/ п варианта |
Исходные данные |
Разрывное усилие каната |
||||
|
Q, |
α, град |
m |
Р расч |
Р табл |
dК |
|
|
1 |
1000 |
15 |
2 |
|||
|
2 |
500 |
30 |
2 |
|||
|
3 |
800 |
45 |
4 |
|||
|
4 |
2500 |
15 |
4 |
|||
|
5 |
3200 |
30 |
4 |
|||
|
6 |
4500 |
45 |
4 |
|||
|
7 |
6100 |
15 |
2 |
|||
|
8 |
5700 |
15 |
4 |
|||
|
9 |
1550 |
45 |
2 |
|||
|
10 |
3900 |
30 |
4 |
Примечание.
Q
– масса груза, кг; угол α, град – угол
отклонения стропа от вертикали; m
– число ветвей строп ; Р расч – разрывное
усилие каната расчетное, кгс; Р табл –
разрывное усилие каната табличное,
кгс; dК
– диаметр каната, мм.
Отчет о работе
Отчет включает в
себя следующие пункты:
1. Цель работы:
изучение и исследование такелажной
оснастки для
монтажных работ.
2. Описание
классификации такелажного оборудования.
3. Характеристику
вида чалочных узлов и пользование ими
на практике.
4. Пользоваться
ручной рычажной лебедкой.
5. Расчет усилий
в канатах по исходным данным, выданным
преподавателем.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое разрывное усилие каната?
Стальная канатная продукция (троса) – распространенная и весьма востребованная разновидность металлоизделий. Производимый сегодня ассортимент канатов способен удовлетворить спрос на них во всех отраслях, где троса востребованы. При выборе метиза для определенных целей приходится считаться с рядом факторов. Определяющими из них являются прочностные характеристики, приведенные в заводском паспорте канатной продукции. Важным параметром принято считать разрывные усилия канатов – предельные нагрузки, сопровождающиеся разрушением витого изделия.
На практике прочность канатной продукции зависит от целого комплекса особенностей изделия, среди которых следует назвать:
- конструкцию троса, определяемую ГОСТом, в соответствии с которым он изготовлен;
- маркировочную группу каната, указывающую на прочностные характеристики;
- диаметры и сечения проволок, из которых он свит и пр.
В конечном итоге разрывное усилие троса зависит от диаметра самого изделия и рост его пропорционален увеличению сечения каната.
Понятия и характеристики
Трактовка понятия разрывного усилия стальных канатов вытекает из самого термина. По сути, это силовая нагрузка, которую необходимо приложить к тросу для его разрушения. Существует два значения этой характеристики канатной продукции, обычно приводимых в стандарте на трос стальной. Они представлены:
• разрывным усилием каната в целом;
• суммарным разрывным усилием каната.
Первое из них определяется на каждую партию канатной продукции посредством заводских испытаний. И если с первым все понятно, то суммарное значение складывается из разрывных усилий всех проволок, пошедших на повив каната. Обычно это значение выше, нежели для канатного изделия целиком, так величина разрывного усилия каната ГОСТ 2688 составляет примерно 84.9% от суммы всех проволок.
Важной характеристикой, определяющей прочность канатной продукции можно назвать упомянутую выше маркировочную группу. Она указывает на временное сопротивление разрыву проволок и измеряется в Н/мм² (кгс/мм²). Фактически это сила, приложенная к проволоке, превышение которой приводит к разрыву последней. Среди серийно производимой канатной продукции встречаются маркировочные группы: 1370 (140) … 1860 (190) Н/мм² (кгс/мм²). Более высокие показатели прочности используются для выполнения специальных заказов. Троса от 1960 Н/мм² (200 кгс/мм²) и выше производятся по согласованию с заказчиком.
Практический расчет разрывного усилия каната (Q_раз) производится несложно. Для него следует воспользоваться формулой:
где k – коэффициент, указывающий на запас прочности, а P – расчетная (рабочая) нагрузка, при которой намечается эксплуатация троса.
Чтобы определиться с коэффициентом, необходимо разделить два термина, приведенные в формуле. Разрывной нагрузке мы посвятили предыдущие строки, а рабочая указывает на вес груза, перемещаемого при помощи троса. Для безопасной работы она всегда меньше, нежели величина статического разрывного усилия каната. Коэффициента запаса прочности значение соответственно в разы больше единицы и равно:
k = Q_раз/P.
Приобретая канатную продукцию для определенных целей, следует учитывать оба вида нагрузки – это важно для продолжительной и безупречной ее работы.
Как выбрать нужный трос?
В случае необходимости выбрать канат по разрывному усилию, можно воспользоваться таблицей, размещенной на этой странице. Приведенные в ней данные учитывают все требования действующих стандартов на предлагаемую нами продукцию. Используя эту информацию можно подобрать трос, максимально пригодный для целей потребителя.
Загрузить PDF
Загрузить PDF
В физике, сила натяжения — это сила, действующая на веревку, шнур, кабель или похожий объект или группу объектов. Все, что натянуто, подвешено, поддерживается или качается на веревке, шнуре, кабеле и так далее, является объектом силы натяжения. Подобно всем силам, натяжение может ускорять объекты или становиться причиной их деформации. Умение рассчитывать силу натяжения является важным навыком не только для студентов физического факультета, но и для инженеров, архитекторов; те, кто строит устойчивые дома, должны знать, выдержит ли определенная веревка или кабель силу натяжения от веса объекта так, чтобы они не проседали и не разрушались. Приступайте к чтению статьи, чтобы научиться рассчитывать силу натяжения в некоторых физических системах.
-
1
Определите силы на каждом из концов нити. Сила натяжения данной нити, веревки является результатом сил, натягивающих веревку с каждого конца. Напоминаем, сила = масса × ускорение. Предполагая, что веревка натянута туго, любое изменение ускорения или массы объекта, подвешенного на веревке, приведет к изменению силы натяжения в самой веревке. Не забывайте о постоянном ускорении силы тяжести — даже если система находится в покое, ее составляющие являются объектами действия силы тяжести. Мы можем предположить, что сила натяжения данной веревки это T = (m × g) + (m × a), где «g» — это ускорение силы тяжести любого из объектов, поддерживаемых веревкой, и «а» — это любое другое ускорение, действующее на объекты.
- Для решения множества физических задач, мы предполагаем идеальную веревку — другими словами, наша веревка тонкая, не обладает массой и не может растягиваться или рваться.
- Для примера, давайте рассмотрим систему, в которой груз подвешен к деревянной балке с помощью одной веревки (смотрите на изображение). Ни сам груз, ни веревка не двигаются — система находится в покое. Вследствие этого, нам известно, чтобы груз находился в равновесии, сила натяжения должна быть равна силе тяжести. Другими словами, Сила натяжения (Ft) = Сила тяжести (Fg) = m × g.
- Предположим, что груз имеет массу 10 кг, следовательно, сила натяжения равна 10 кг × 9,8 м/с2 = 98 Ньютонов.
-
2
Учитывайте ускорение. Сила тяжести — не единственная сила, что может влиять на силу натяжения веревки — такое же действие производит любая сила, приложенная к объекту на веревке с ускорением. Если, к примеру, подвешенный на веревке или кабеле объект ускоряется под действием силы, то сила ускорения (масса × ускорение) добавляется к силе натяжения, образованной весом этого объекта.
- Предположим, что в нашем примере на веревку подвешен груз 10 кг, и вместо того, чтобы быть прикрепленным к деревянной балке, его тянут вверх с ускорением 1 м/с2. В этом случае, нам необходимо учесть ускорение груза, также как и ускорение силы тяжести, следующим образом:
- Ft = Fg + m × a
- Ft = 98 + 10 кг × 1 м/с2
- Ft = 108 Ньютонов.
- Предположим, что в нашем примере на веревку подвешен груз 10 кг, и вместо того, чтобы быть прикрепленным к деревянной балке, его тянут вверх с ускорением 1 м/с2. В этом случае, нам необходимо учесть ускорение груза, также как и ускорение силы тяжести, следующим образом:
-
3
Учитывайте угловое ускорение. Объект на веревке, вращающийся вокруг точки, которая считается центром (как маятник), оказывает натяжение на веревку посредством центробежной силы. Центробежная сила — дополнительная сила натяжения, которую вызывает веревка, «толкая» ее внутрь так, чтобы груз продолжал двигаться по дуге, а не по прямой. Чем быстрее движется объект, тем больше центробежная сила. Центробежная сила (Fc) равна m × v2/r где «m»– это масса, «v» — это скорость, и «r» — радиус окружности, по которой движется груз.
- Так как направление и значение центробежной силы меняются в зависимости от того, как объект движется и меняет свою скорость, то полное натяжение веревки всегда параллельно веревке в центральной точке. Запомните, что сила притяжения постоянно действует на объект и тянет его вниз. Так что, если объект раскачивается вертикально, полное натяжение сильнее всего в нижней точке дуги (для маятника это называется точкой равновесия), когда объект достигает максимальной скорости, и слабее всего в верхней точке дуги, когда объект замедляется.
- Давайте предположим, что в нашем примере объект больше не ускоряется вверх, а раскачивается как маятник. Пусть наша веревка будет длиной 1,5 м, а наш груз движется со скоростью 2 м/с, при прохождении через нижнюю точку размаха. Если нам нужно рассчитать силу натяжения в нижней точке дуги, когда она наибольшая, то сначала надо выяснить равное ли давление силы тяжести испытывает груз в этой точке, как и при состоянии покоя — 98 Ньютонов. Чтобы найти дополнительную центробежную силу, нам необходимо решить следующее:
- Fc = m × v2/r
- Fc = 10 × 22/1.5
- Fc =10 × 2,67 = 26,7 Ньютонов.
- Таким образом, полное натяжение будет 98 + 26,7 = 124,7 Ньютона.
-
4
Учтите, что сила натяжения благодаря силе тяжести меняется по мере прохождения груза по дуге. Как было отмечено выше, направление и величина центробежной силы меняются по мере того, как качается объект. В любом случае, хотя сила тяжести и остается постоянной, результирующая сила натяжения в результате тяжести тоже меняется. Когда качающийся объект находится не в нижней точке дуги (точке равновесия), сила тяжести тянет его вниз, но сила натяжения тянет его вверх под углом. По этой причине сила натяжения должна противодействовать части силы тяжести, а не всей ее полноте.
- Разделение силы гравитации на два вектора сможет помочь вам визуально изобразить это состояние. В любой точке дуги вертикально раскачивающегося объекта, веревка составляет угол «θ» с линией, проходящей через точку равновесия и центр вращения. Как только маятник начинает раскачиваться, сила гравитации (m × g) разбивается на 2 вектора — mgsin(θ), действуя по касательной к дуге в направлении точки равновесия и mgcos(θ), действуя параллельно силе натяжения, но в противоположном направлении. Натяжение может только противостоять mgcos(θ) — силе, направленной против нее — не всей силе тяготения (исключая точку равновесия, где все силы одинаковы).
- Давайте предположим, что, когда маятник отклоняется на угол 15 градусов от вертикали, он движется со скоростью 1,5 м/с. Мы найдем силу натяжения следующими действиями:
- Отношение силы натяжения к силе тяготения (Tg) = 98cos(15) = 98(0,96) = 94,08 Ньютона
- Центробежная сила (Fc) = 10 × 1,52/1,5 = 10 × 1,5 = 15 Ньютонов
- Полное натяжение = Tg + Fc = 94,08 + 15 = 109,08 Ньютонов.
-
5
Рассчитайте трение. Любой объект, который тянется веревкой и испытывает силу «торможения» от трения другого объекта (или жидкости), передает это воздействие натяжению в веревке. Сила трения между двумя объектами рассчитывается также, как и в любой другой ситуации — по следующему уравнению: Сила трения (обычно пишется как Fr) = (mu)N, где mu — это коэффициент силы трения между объектами и N — обычная сила взаимодействия между объектами, или та сила, с которой они давят друг на друга. Отметим, что трение покоя — это трение, которое возникает в результате попытки привести объект, находящийся в покое, в движение — отличается от трения движения — трения, возникающего в результате попытки заставить движущийся объект продолжать движение.
- Давайте предположим, что наш груз в 10 кг больше не раскачивается, теперь его буксируют по горизонтальной плоскости с помощью веревки. Предположим, что коэффициент трения движения земли равен 0,5 и наш груз движется с постоянной скоростью, но нам нужно придать ему ускорение 1м/с2. Эта проблема представляет два важных изменения — первое, нам больше не нужно рассчитывать силу натяжения по отношению к силе тяжести, так как наша веревка не удерживает груз на весу. Второе, нам придется рассчитать натяжение, обусловленное трением, также как и вызванное ускорением массы груза. Нам нужно решить следующее:
- Обычная сила (N) = 10 кг & × 9,8 (ускорение силы тяжести) = 98 N
- Сила трения движения (Fr) = 0,5 × 98 N = 49 Ньютонов
- Сила ускорения (Fa) = 10 kg × 1 м/с2 = 10 Ньютонов
- Общее натяжение = Fr + Fa = 49 + 10 = 59 Ньютонов.
Реклама
- Давайте предположим, что наш груз в 10 кг больше не раскачивается, теперь его буксируют по горизонтальной плоскости с помощью веревки. Предположим, что коэффициент трения движения земли равен 0,5 и наш груз движется с постоянной скоростью, но нам нужно придать ему ускорение 1м/с2. Эта проблема представляет два важных изменения — первое, нам больше не нужно рассчитывать силу натяжения по отношению к силе тяжести, так как наша веревка не удерживает груз на весу. Второе, нам придется рассчитать натяжение, обусловленное трением, также как и вызванное ускорением массы груза. Нам нужно решить следующее:
-
1
Поднимите вертикальные параллельные грузы с помощью блока. Блоки — это простые механизмы, состоящие из подвесного диска, что позволяет менять направление силы натяжения веревки. В простой конфигурации блока, веревка или кабель идет от подвешенного груза вверх к блоку, затем вниз к другому грузу, создавая тем самым два участка веревки или кабеля. В любом случае натяжение в каждом из участков будет одинаковым, даже если оба конца будут натягиваться силами разных величин. Для системы двух масс, подвешенных вертикально в блоке, сила натяжения равна 2g(m1)(m2)/(m2+m1), где «g» — ускорение силы тяжести, «m1» — масса первого объекта, «m2»– масса второго объекта.
- Отметим следующее, физические задачи предполагают, что блоки идеальны — не имеют массы, трения, они не ломаются, не деформируются и не отделяются от веревки, которая их поддерживает.
- Давайте предположим, что у нас есть два вертикально подвешенных на параллельных концах веревки груза. У одного груза масса 10 кг, а у второго — 5 кг. В этом случае, нам необходимо рассчитать следующее:
- T = 2g(m1)(m2)/(m2+m1)
- T = 2(9,8)(10)(5)/(5 + 10)
- T = 19,6(50)/(15)
- T = 980/15
- T = 65,33 Ньютонов.
- Отметим, что, так как один груз тяжелее, все остальные элементы равны, эта система начнет ускоряться, следовательно, груз 10 кг будет двигаться вниз, заставляя второй груз идти вверх.
-
2
Подвесьте грузы, используя блоки с не параллельными вертикальными нитями. Блоки зачастую используются для того, чтобы направлять силу натяжения в направлении, отличном от направления вниз или вверх. Если, к примеру, груз подвешен вертикально к одному концу веревки, а другой конец держит груз в диагональной плоскости, то непараллельная система блоков принимает форму треугольника с углами в точках с первых грузом, вторым и самим блоком. В этом случае натяжение в веревке зависит как от силы тяжести, так и от составляющей силы натяжения, которая параллельна к диагональной части веревки.
- Давайте предположим, что у нас есть система с грузом в 10 кг (m1), подвешенным вертикально, соединенный с грузом в 5 кг(m2), расположенным на наклонной плоскости в 60 градусов (считается, что этот уклон не дает трения). Чтобы найти натяжение в веревке, самым легким путем будет сначала составить уравнения для сил, ускоряющих грузы. Далее действуем так:
- Подвешенный груз тяжелее, здесь нет трения, так что мы знаем, что он ускоряется вниз. Натяжение в веревке тянет вверх, так что он ускоряется по отношению к равнодействующей силе F = m1(g) — T, или 10(9,8) — T = 98 — T.
- Мы знаем, что груз на наклонной плоскости ускоряется вверх. Так как она не имеет трения, мы знаем, что натяжение тянет груз вверх по плоскости, а вниз его тянет только свой собственный вес. Составляющая силы, тянущей вниз по наклонной, вычисляется как mgsin(θ), так что в нашем случае мы можем заключить, что он ускоряется по отношению к равнодействующей силе F = T — m2(g)sin(60) = T — 5(9,8)(0,87) = T — 42,14.
- Если мы приравняем эти два уравнения, то получится 98 — T = T — 42,14. Находим Т и получаем 2T = 140,14, или T = 70,07 Ньютонов.
- Давайте предположим, что у нас есть система с грузом в 10 кг (m1), подвешенным вертикально, соединенный с грузом в 5 кг(m2), расположенным на наклонной плоскости в 60 градусов (считается, что этот уклон не дает трения). Чтобы найти натяжение в веревке, самым легким путем будет сначала составить уравнения для сил, ускоряющих грузы. Далее действуем так:
-
3
Используйте несколько нитей, чтобы подвесить объект. В заключение, давайте представим, что объект подвешен на «Y-образной» системе веревок — две веревки закреплены на потолке и встречаются в центральной точке, из которой идет третья веревка с грузом. Сила натяжения третьей веревки очевидна — простое натяжение в результате действия силы тяжести или m(g). Натяжения на двух остальных веревках различаются и должны составлять в сумме силу, равную силе тяжести вверх в вертикальном положении и равны нулю в обоих горизонтальных направлениях, если предположить, что система находится в состоянии покоя. Натяжение в веревке зависит от массы подвешенных грузов и от угла, на который отклоняется от потолка каждая из веревок.
- Давайте предположим, что в нашей Y-образной системе нижний груз имеет массу 10 кг и подвешен на двух веревках, угол одной из которых составляет с потолком 30 градусов, а угол второй — 60 градусов. Если нам нужно найти натяжение в каждой из веревок, нам понадобится рассчитать горизонтальную и вертикальную составляющие натяжения. Чтобы найти T1 (натяжение в той веревке, наклон которой 30 градусов) и T2 (натяжение в той веревке, наклон которой 60 градусов), нужно решить:
- Согласно законам тригонометрии, отношение между T = m(g) и T1 и T2 равно косинусу угла между каждой из веревок и потолком. Для T1, cos(30) = 0,87, как для T2, cos(60) = 0,5
- Умножьте натяжение в нижней веревке (T=mg) на косинус каждого угла, чтобы найти T1 и T2.
- T1 = 0,87 × m(g) = 0,87 × 10(9,8) = 85,26 Ньютонов.
- T2 =0,5 × m(g) = 0,5 × 10(9,8) = 49 Ньютонов.
Реклама
- Давайте предположим, что в нашей Y-образной системе нижний груз имеет массу 10 кг и подвешен на двух веревках, угол одной из которых составляет с потолком 30 градусов, а угол второй — 60 градусов. Если нам нужно найти натяжение в каждой из веревок, нам понадобится рассчитать горизонтальную и вертикальную составляющие натяжения. Чтобы найти T1 (натяжение в той веревке, наклон которой 30 градусов) и T2 (натяжение в той веревке, наклон которой 60 градусов), нужно решить:
Об этой статье
Эту страницу просматривали 287 682 раза.
Была ли эта статья полезной?
Усилия в тросе при поднятии (опускании) груза
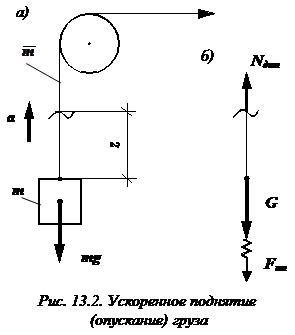
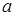
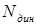
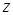
Отбросим движущиеся массы груза и участка троса длиной z и заменим их действие на безмассовый упругий скелет троса силой их веса 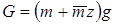
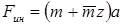
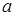
Из уравнения равновесия находим динамическое усилие: 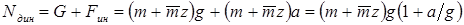
Если бы груз был статичен, то продольная сила 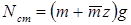
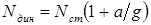
Коэффициент динамичности позволяет оценить действие динамической нагрузки на практике: 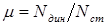
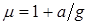
При поднятии груза с ускорением 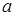
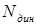
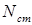
При свободном падении груза, когда 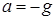
Определить усилия в тросе AB и в стержнях AC и AD, поддерживающих груз Q веса 180 Н, если AB=170 см, AC=AD=100 см, CD=120 см; CK=KD и плоскость ΔCDA горизонтальна. Крепления стержней в точках A, C и D шарнирные.


 анаты
анаты