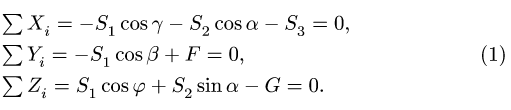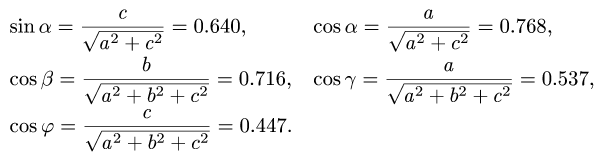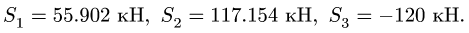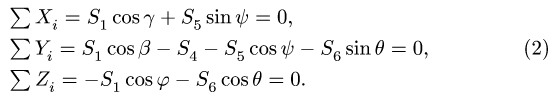Рассмотрим
нахождение реакций в шарнире A
от действия
первого кривошипно-ползунного механизма
(звенья 1,2,3).
Для нахождения
тангенциальной составляющей реакции
в шарнире A
,
указали все силы и моменты, действующие
на первый кривошипно-ползунный механизм,
и составили уравнение моментов
относительно шарнира B . Это уравнение
имеет вид:
где lAB=l2=0,152
– плечо силы
;
hФS2—
плечо силы ФS2,
hФS2=0,046
м;
hG2—
плечо силы G2,
hG2=0,105
м;
Получили
=102,4
Н.
Для нахождения
полной реакции в шарнире А составили
векторное уравнение:
Строим
план сил в масштабе F=0,37
мм/Н.Откуда получаем:
Н.
Н.
Аналогичные
операции провели для другого
кривошипо-ползунного механизма (звенья
1,4,5) и получили следующие результаты:
;
.
3.4.2
Определение усилий в шарнире В.
Для нахождения
полной реакции в шарнире B (F32)
проставили все силы, действующие на
поршень 3, и составили векторное уравнение
сил действующих на поршень 3:
.
Был построен план
сил в масштабе F=0,37
мм/Н, откуда получили значение силы:
.
3.4.3. Определение усилий в шарнире с.
Для нахождения
полной реакции в шарнире F
(F54)
проставили все силы, действующие на
поршень 5, и составили векторное уравнение
сил действующих на поршень 5:
.
Был
построен план сил в масштабе F=0,05
мм/Н, откуда получили значение силы:
3.5. Определение усилий в шарнире о и момента сопротивления.
Для определения
полной реакции в шарнире О составим
векторное уравнение:
,
где
—
силы найденные выше,
Был построен план
сил в масштабе F=0,028
мм/Н,
Получили: F10
= 4057 H
Момент сопротивления
определяется из условия равновесия
механизма относительно шарнира О, для
этого записываем уравнение моментов
относительно точки О:
MФ1+
(Mcпр)*—
M(F14)+
M(F12)=0.
где
Получили:
с первого листа
проекта составляет 13 Н*м.
Таким образом,
погрешность составляет:
4. Синтез кулачкового механизма.
Исходные
данные для проектирования кулачкового
механизма:
угол рабочего
профиля кулачка
°.
Ход толкателя в
кулачковом приводе клапанов h=0,007
м.
Максимально
допустимый угол в кулачковом механизме
=30°.
соотношение между ускорениями толкателя
a1/a2=1,7.
4.1. Построение графика заданного закона движения.
Производиться
проектирование кулачкового механизма
впускного клапана. Закон изменения
ускорения толкателя приведен в техническом
задании в виде графика. В механизме
используется толкатель с роликом. В
качестве обобщенной координаты
принимается угол поворота кулачка.
Так как исходная
функция задана в виде графика, то решение
получают при помощи метода графического
интегрирования. Для определения
передаточной функции скорости толкателя
интегрируют заданную функцию ускорения
толкателя, затем интегрируют полученную
функцию скорости и находят функцию
перемещения толкателя.
Все
три графика располагают один под другим
на одинаковой базе по оси абсцисс;
.
Масштаб по осивычисляют по формуле
.
Построив график
ускорения, построили график скорости
методом графического интегрирования,
выбрав отрезок интегрирования К1=39мм.
Интегрируя график
скорости (с отрезком интегрирования
K2=35мм),
получили график перемещения т.В толкателя.
Полученную ломаную линию заменяем
плавной кривой.
Расчет масштабов:
На
графике перемещений уmax
получили автоматически, и его величина
зависит от отрезка К. Тогда, зная ход
толкателя, масштаб перемещения будет:
.
Построим
графики кинематических передаточных
функций скорости и ускорения. Тогда:
В
условии сказано, что вращение
распределительному валу 7 передаётся
от коленчатого вала 1 парой зубчатых
колёс 10 и 11,передаточное отношение
которой i=2.Отсюда
находим угловую скорость вращения
кулачка wи=w1ср/2=136/2=68
рад/с. Находим
масштаб времени mt=mf*wи=116,4*68=7915,2
мм/с.
Зная
масштаб времени находим масштабы
скорости и ускорения.
Масштаб
скорости:
2,
.
Масштаб
ускорения:
1,
.
Строим
графики скорости и ускорения.
Соседние файлы в папке 16-й курсач
- #
04.03.2014147.87 Кб70Лидия-Л3 итог.frw
- #
04.03.201477.59 Кб72Лидия-Л3.bak
- #
04.03.201494.44 Кб69Лидия-Л4 итог.bak
- #
04.03.201494.44 Кб80Лидия-Л4 итог.dwg
- #
04.03.201458.75 Кб70Попус-Л1.bak
- #
- #
Пример решения задачи по определению усилий в двух стержнях, скрепленных шарнирно между собой и с вертикальной опорной стеной, в точке соединения которых подвешен груз.
Задача
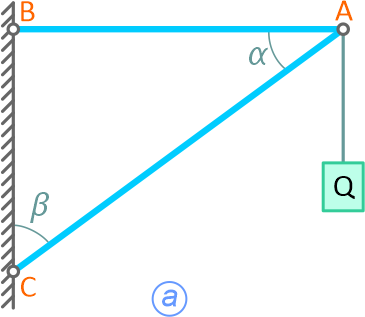
Груз Q=1000Н удерживается с помощью двух невесомых стержней, шарнирно скрепленных между собой в точке A и в шарнирах B и C с вертикальной стеной (α=60°, β=30°).
Рисунок 2.1
Определить усилия в стержнях AB и BC (рисунок 2.1,а).
Другие примеры решений >
Помощь с решением задач >
Решение
Короткое видео про реакции в разных типах связей:
Другие видео
В данном случае следует рассмотреть равновесие точки A, т.к. все силы приложены в этой точке.
Нить с грузом натянута силой Q. В равновесии точку A удерживают два невесомых стержня. Их реакции всегда направлены вдоль стержней.
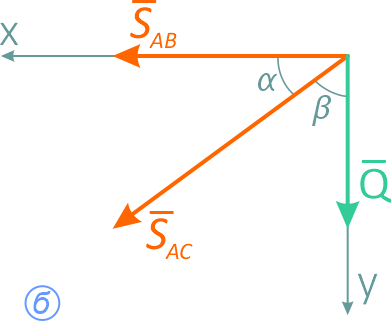
Реакции принято направлять от узла (точки A), т.е. предполагается, что стержни работают на растяжение (рисунок 2.1, б). В случае отрицательного ответа при решении уравнений стержень работает на сжатие.
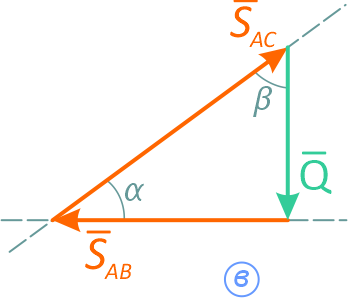
При равновесии системы сил выполняется равенство
Это векторное равенство можно построить. Откладываем в масштабе известную силу Q, к концу вектора прибавляем SAB, т.к. его величина и направление неизвестны, проводим через конец вектора Q горизонтальную линию (параллельно SAB, рисунок 2.1, б).
Замыкающий вектор SAC должен пройти через начало вектора Q под углом β к вертикали. Результатом построения является замкнутый треугольник (рисунок 2.1, в). Величины усилий в стержнях можно получить, умножая замеренные значения векторов сил на масштаб или воспользовавшись теоремой синусов:
Направление силы SAC в силовом треугольнике говорит о том, что этот стержень работает на сжатие.
Задача может быть решена и аналитически. Для этого выбираем систему координат xAy (рисунок 2.1, б) и проецируем на ее оси векторное равенство (2.3):
При этом
После решения уравнений равновесия находим
То есть и в этом решении по знакам в ответах получаем, что стержень AC работает на сжатие, а стержень AB – на растяжение.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Содержание:
Расчет ферм:
При устройстве перекрытий, постройке мостов, кранов, мачт для высоковольтных линий и т. п. применяются конструкции, называемые фермами.
Фермой называется геометрически неизменяемая система, состоящая из невесомых стержней, соединенных между собой по концам шарнирами. Места соединения стержней между собой называются узлами фермы.
Обычно в фермах соединение стержней в узлах осуществляется при помощи клепки или сварки, шарнирное же соединение стержней вводится лишь для облегчения расчета ферм, что приводит к сравнительно небольшим ошибкам в вычислении по сравнению с действительными конструкциями.
Фермы, у которых оси всех стержней расположены в одной плоскости, называются плоскими. В дальнейшем мы ограничимся рассмотрением плоских ферм.
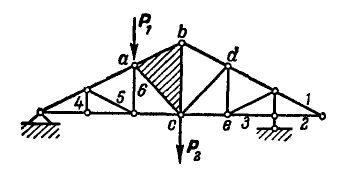
Всякая ферма состоит из ряда стержневых треугольников, соединенных в узлах шарнирно (рис. 79).
Рис. 79.
Для образования фермы мы должны взять основной треугольник, хотя бы abc, и к нему последовательно присоединять каждый узел d, е и т. д. двумя стержнями. Если ферма состоит из
При расчете фермы, т. е. при определении усилий во всех ее стержнях, мы можем для каждого узла составить два уравнения равновесия, а для 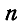
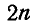
Отсюда следует, что число неизвестных усилий, определяемое числом стержней, сложение с числом опорных реакций не должно превышать общего числа уравнений статики 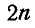
Для определения усилий в стержнях ферм обычно применяют один из следующих трех способов: последовательное вырезание узлов, построение диаграммы Кремона, проведение сквозных сечений (Риттера).
При применении каждого из перечисленных способов следует предварительно по заданным силам, приложенным к ферме, определить опорные реакции (аналитически или графически) и только после этого переходить к определению усилий в стержнях фермы.
Определение усилий по способу последовательного вырезания узлов
Определение усилий по способу последовательного вырезания узлов заключается в том, что последовательно рассматривают равновесие каждого узла фермы и для рассматриваемого узла либо составляют два уравнения равновесия в форме 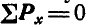
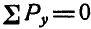
При этом порядок рассмотрения равновесия узлов безразличен, лишь бы в рассматриваемом узле число неизвестных усилий не превышало двух.
Выясним применение этого способа на отдельных примерах.
Задача №1
Найти усилия 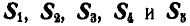
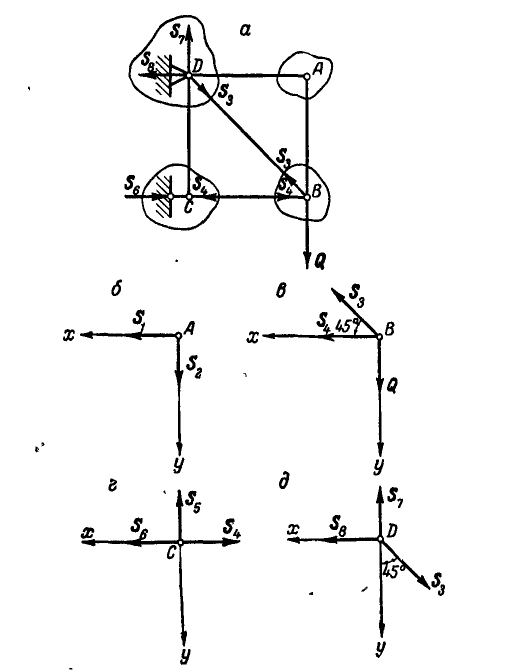
Рис. 80.
Решение. Начнем с рассмотрения равновесия узла А, так как здесь сходятся два неизвестных усилия. Вырежем узел А и взамен пересеченных стержней введем силы 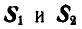
Вырежем теперь узел В и рассмотрим его равновесие (рис. 80, в):
откуда получаем:
Переходим к рассмотрению равновесия узла С (рис. 80, г):
откуда находим:
Составляя уравнения равновесия для точки D (рис. 80, д), имеем:
откуда
Для усилия 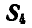
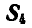
Правильное направление стрелок усилий показано на рисунке 80, а.
Иногда при определении усилий в стержнях полезно сразу выделить те стержни, усилия в которых равны нулю (нулевые стержни). Из рассмотрений равновесия узлов А и С (рис. 80, б и. 80, г) заключаем:
1. Если имеется узел А, в котором сходятся два стержня, то при отсутствии других сил, приложенных к узлу, усилия в этих стержнях равны нулю.
2. Если имеется узел С, где сходятся три стержня, из которых два направлены по одной прямой, а третий примыкает к узлу под любым углом, то при отсутствии других сил, приложенных к узлу, усилие в третьем стержне равно нулю. На основании этого можно сказать, что усилия в стержнях 1, 2, 3, 4, 5 и 6 фермы (рис. 79) равны нулю.
Задача №2
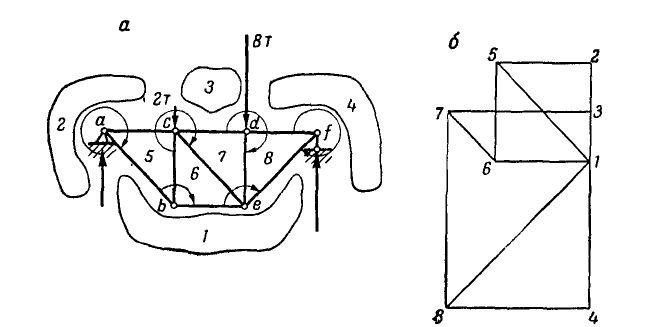
Сцепка состоит из четырех тросов АО, ВО, АС и ВС, образующих квадрат (рис. 81, а).
Между точками А и В по диагонали квадрата вставлен брус, а в точках А, В и С приложены вертикальные силы Q = 500 кГ каждая. Определить натяжения 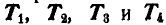
Решение. Из рассмотрения равновесия точки С (рис. 81, б) имеем:
откуда:
Переходим к рассмотрению равновесия узла А (рис. 81, в):
откуда
Рис. 81.
В силу симметрии узлов А и В заключаем, что 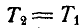
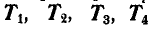
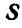
Задача №3
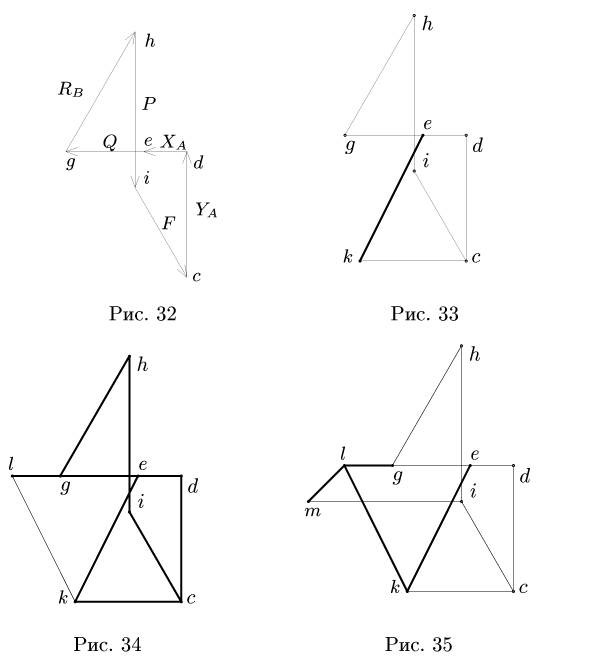
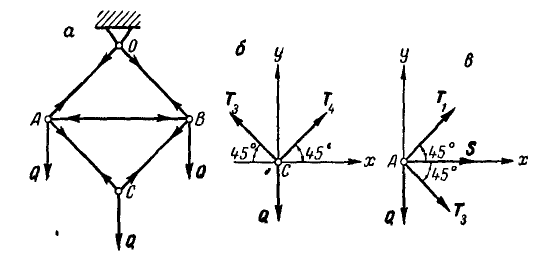
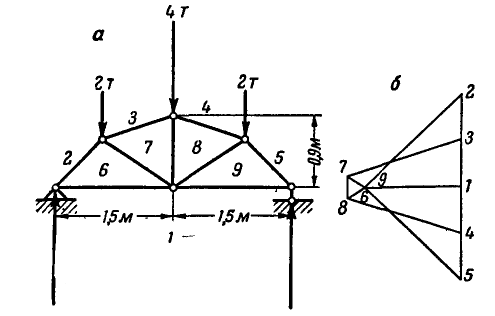
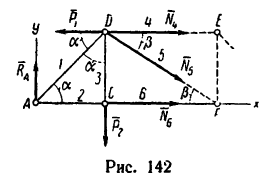
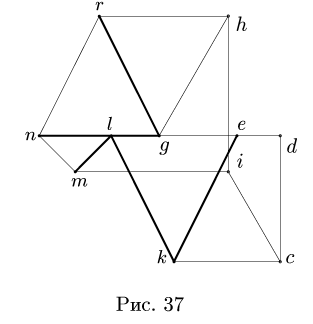
В точках А и F шарнирной стержневой системы (рис. 82, а), внешний контур которой совпадает со сторонами правильного шестиугольника, приложены силы 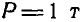
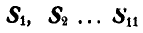
Рис. 82.
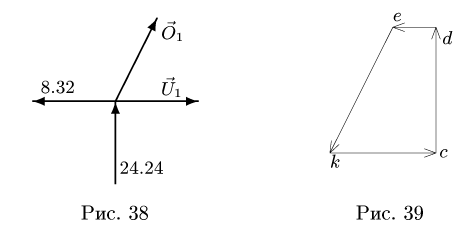
Решение. Эту задачу проще всего решить геометрическим способом, построив для каждого из узлов замкнутый треугольник сил. Рассмотрим сначала равновесие точки А (можно F). Отложим в выбранном масштабе силу Р (рис. 82, б) и из начала и конца этой силы проведем направления, параллельные стержням 1 и 6, до их взаимного пересечения. В полученном треугольнике равновесия стрелки сил 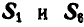
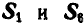
При построении треугольника равновесия для точки В известной нам силой является реакция 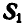
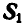
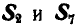
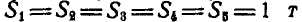
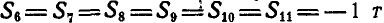
Задача №4
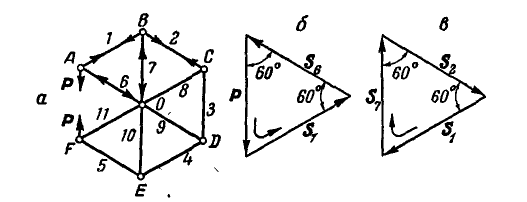
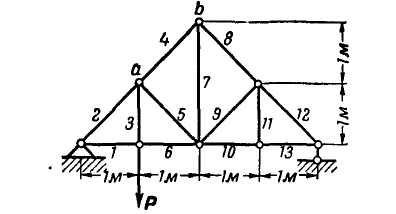
Способом последовательного вырезания узлов определить усилия во всех стержнях ферм (рис. 83 и 84).
Рис. 83. Рис. 84.
Ответ (к рис. 83).
Таблица 1
Ответ (к рис. 84).
Таблица 2
Определение усилий в стержнях ферм по способу построения диаграммы Кремона
Идея этого графического способа проста и заключается в построении для узлов фермы, находящихся в равновесии, замкнутых многоугольников сил, образующих диаграмму.
Пусть требуется найти усилия во всех стержнях фермы (рис. 85, а) при действии на нее заданных сил 2 т и 8 т. Известными нам способами находим, что левая опорная реакция равна 4 т, а правая 6 т.
Для облегчения построения диаграммы введем в рассмотрение внешние и внутренние поля. Под внешними полями будем понимать части плоскости, ограниченные с боков внешними силами (заданными и реактивными) и внешним контуром фермы, под внутренними полями — части плоскости, ограниченные стержнями фермы.
Рис. 85.
Условимся нумерацию внешних полей 1, 2, 3 и 4 (рис. 85, а) производить по направлению движения стрелки часов, внутренних 5, 6, 7, 8 — слева направо, а усилия, сходящиеся в каждом узле обозначать двойными цифрами смежных полей, производя обход усилий в каждом узле по часовой стрелке. Так, например, в узле а сходятся три усилия: 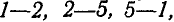
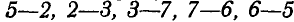
Выбрав масштаб сил, например 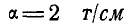
Построение диаграммы следует начинать для того узла, в котором сходятся не более двух стержней. В нашем случае такими узлами являются 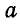
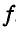
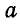
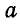
Теперь можно перейти к следующему узлу, где сходятся два неизвестных усилия; таким узлом является 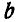
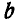
Переходим к узлу с. Здесь сходятся усилия 6—5, 5—2, 2—3, имеющиеся на диаграмме, и неизвестные 3—7 и 7—6. Проводим из точки 3 диаграммы направление, параллельное стержню 3—7, а из точки 6 направление, параллельное стержню 7—6; в пересечении этих направлений получаем на диаграмме точку 7. Подобные построения можно провести для остальных узлов. Узел 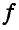
Имея диаграмму Кремона (рис. 85, б), можно:
1. Проверять правильность построенной диаграммы, основываясь на том, что многоугольник сил для каждого узла должен быть замкнут. Возьмем, например, узел d, в котором сходятся усилия 7—3, 3—4, 4—8, 8—7. Мы видим, что эти усилия на диаграмме образуют замкнутый многоугольник.
2. Определять величину и знак усилия в любом стержне, примыкающем к какому-либо узлу. Так, например, если возьмем стержень 3—7, примыкающий к узлу с (если бы мы переставили цифры и рассматривали стержень 7—3, то тогда мы обязаны были бы его отнести к узлу d), то на диаграмме величина усилия, возникающего в этом стержне, выражается отрезком 3—7, умноженным на масштаб, а направление будет к узлу с, так как на диаграмме усилие 3—7 читается от 3 к 7, т. е. справа налево. Точно так же усилие в стержне 7—6 изобразится на диаграмме отрезком 7—6, умноженным на масштаб α , а направление усилия будет от узла с, так как при чтении усилия 7—6 на диаграмме оно направлено от 7 к 6, т. е. сверху вниз по диагонали. Следовательно, в первом случае мы имеем сжатие (—), во втором — растяжение (+).
Задача №5
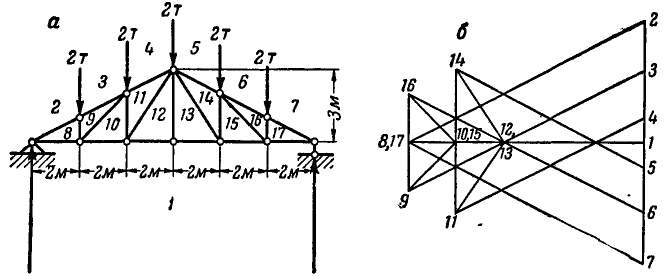
Определить усилия в стержнях ферм путем построения диаграммы Кремона (рис. 86, а и 87, а).
Рис. 86.
Рис. 87.
Решение. На рисунках 86, б и 87, б приведено построение диаграмм.
Определение усилий в стержнях ферм по способу сквозных сечений
Особенность этого способа состоит в том, что он позволяет определять усилие в любом стержне фермы, не определяя усилий в остальных стержнях, что во многих случаях является удобным.
Выясним применение этого способа на отдельном примере.
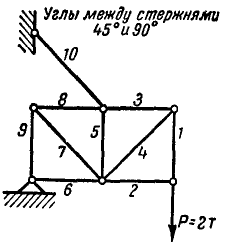
Пусть дана ферма (рис. 88, а), стержни которой образуют между собой углы в 45° и 90°. Определим сначала величины опорных реакций аналитически или способом веревочного многоугольника. Нетрудно видеть, что
Пронумеровав стержни, можно перейти к определению усилий, возникающих в стержнях, по способу сквозных сечений. Положим, требуется найти усилие 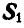
Рассмотрим теперь равновесие одной из частей фермы, расположенной слева или справа от проведенного сечения. В данной задаче удобнее выделить левую часть, так как на нее действует меньше сил (рис. 88, б).
Взамен отброшенной правой части прикладываем реакции стержней 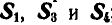
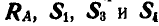

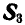
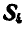

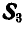
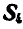
Рис. 88.
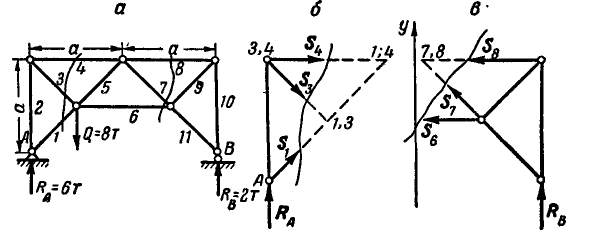
Нетрудно видеть, что таким. уравнением является уравнение моментов относительно той точки, где пересекаются линии действия усилий 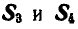
откуда
Чтобы определить усилие 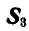
откуда
Для определения усилия 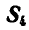
откуда
Знак минус указывает на то, что стержень 4 сжат,
Точки 1, 3; 3, 4 и 1, 4, выбранные таким образом, приводят нас к уравнениям равновесия (36, б).
При определении усилия 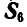
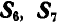
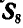
Для определения усилия 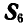
откуда
При определении усилия в стержне 7 следовало бы составить уравнение моментов относительно точки 6, 8, пересечения стержней 6 и 8, но эти стержни параллельны и точка 6, 8 получается в бесконечности; в этом случае вместо уравнения моментов составляют уравнение проекций на ось, перпендикулярную к линиям действия тех реакций стержней, которые параллельны:
откуда
Подобным же способом можно определить усилия и в остальных стержнях.
Преимущество изложенного способа заключается в том, что здесь мы можем определить усилие в любом стержне, не определяя усилий в остальных стержнях.
Рис. 89.
Задача №6
Определить по способу сквозных сечений усилия во всех стержнях фермы (рис. 89).
Указание: предварительно определяем реакцию 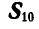
Ответ (к рис. 89) см. в таблице 3.
Таблица 3
Задача №7
По известному усилию в стержне 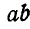
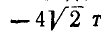
Рис. 90.
Ответ (к рис. 90) см. таблицу 4.
Таблица 4
Статически определимые фермы. Методы вырезания узлов и сквозного сечения
Плоская или пространственная неизменяемая конструкция, составленная из шарнирно соединенных между собой стержней, называется фермой.
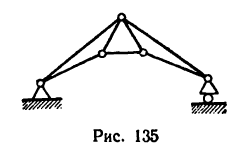
На рис. 135 изображена простая плоская ферма (пример пространственной фермы приведен в § 19-4).
Если число узлов (шарниров) фермы n, а число стержней k, то в простой плоской ферме соблюдается условие
k=2n + 3
Ферма называется статически определимой, если усилия во всех стержнях фермы, нагруженной в шарнирах, можно определить при помощи уравнений равновесия.
Все. плоские простые фермы статически определимы.
Для определения усилий в стержнях ферм употребляются графические или аналитические методы. Рассмотрим только аналитические методы: метод вырезания узлов (задача 103-17) и метод сквозного сечения—метод Риттера (задача 104-17).
При использовании метода вырезания узлов необходимо придерживаться следующего порядка:
- а) выяснить, какие нагрузки действуют на ферму, как они направлены и где приложены, а затем определить реакции связей, используя уравнения равновесия Правильность этой части решения нужно обязательно проверить: для проверки можно использовать любое дополнительно составленное уравнение равновесия;
- б) затем следует определить усилия в стержнях фермы, начиная с того узла, на который действуют не более двух неизвестных сил, так как в каждом случае на узел действует система сходящихся сил и, следовательно, для одного узла можно составить лишь два уравнения равновесия;
- в) вырезав узел, необходимо заменить действие на узел отброшенной части фермы усилиями, действующими вдоль стержней, считая при этом, что все стержни растянуты, а затем составить уравнения равновесия;
- г) путем перехода от узла к узлу определяют усилия во всех стержнях, один из узлов при этом остается нерассмотренным; составив уравнения равновесия для этого узла, можно проверить правильность решения задачи.
При определении усилий в стержнях ферм по методу сквозного сечения необходимо придерживаться следующего порядка:
- а) прежде всего, так же как и при методе вырезания узлов, выявив все нагрузки, определить реакции опор;
- б) мысленно разрезать фермы на две части таким образом, чтобы разрез проходил не более чем через три стержня, усилия в которых неизвестны»1, и, отбросив одну из частей, заменить действие отброшенной части на оставшуюся усилиями, направленными вдоль стержней, предполагая при этом, что все разрезанные стержни (с неизвестными усилиями) растянуты;
- в) составить три уравнения равновесия; при выборе направлений осей проекций, а также центра моментов нужно исходить из того, чтобы в каждое из уравнений по возможности входило не более одной неизвестной силы.
Задача №8
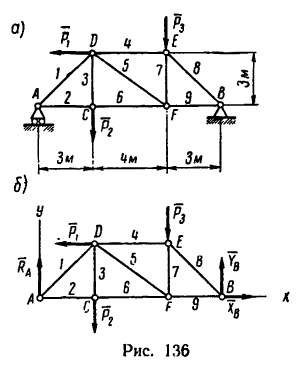
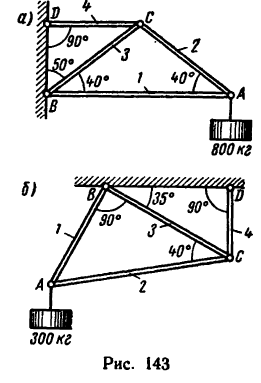
Определить усилия в стержнях фермы, нагруженной, как показано на рис. 136, а, тремя силами: 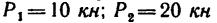
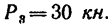
Решение — методом вырезания узлов.
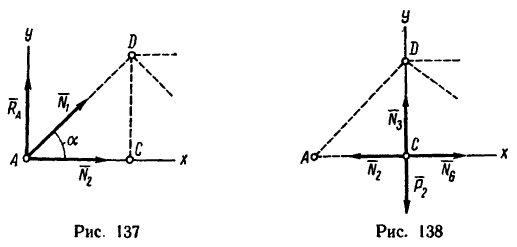
1. Освободим ферму от связей и заменим связи их реакциями. Действие подвижного шарнира А заменим реакцией 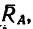
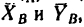
Составим три уравнения равновесия:
Подставив в эти уравнения числовые значения и решив находим (вычисления рекомендуем произвести самостоятельно):
* При разрезании фермы через четыре и большее число стержней образуется плоская система сил с четырьмя или соответственно большим числом неизвестных. Так как для произвольной плоской системы сил можно составить только три уравнения равновесия, задачу решить нельзя.
Для проверки можно использовать уравнение проекций сил на ось у или уравнение моментов сил относительно точки С (или D, или Е, или F).
2. Вырежем узел А, заменив действие на узел отброшенной части фермы силами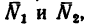
силы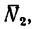
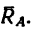
Из уравнения (2)
(стержень 1 сжат).
Из уравнения (1)
(стержень 2 растянут).
3. Вырежем узел С, заменив действие на узел отброшенной части фермы силами 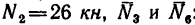
Отсюда
(стержень 6 растянут);
(стержень 3 растянут).
4. Вырежем узел D. В этом случае узел находится в равновесии иод действием пяти сил, три из них известны: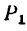
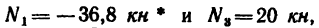
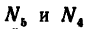
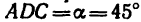
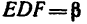
определить, что 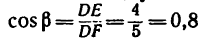
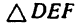
FE=3 л, катет DЕ = 4 м и, следовательно, гипотенуза DF=5 м), a
Составим уравнение равновесия:
Из уравнения (6)
(стержень 5 растянут).
Из уравнения (5)
(стержень 4 сжат).
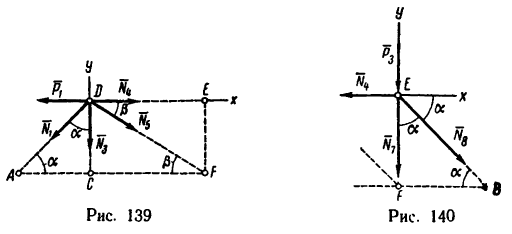
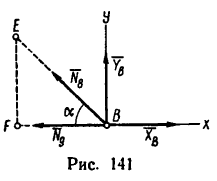
5. Вырежем узел Е, к которому приложены четыре силы: две из них известны (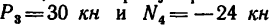
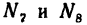
Расположив оси проекций, как показано на рис. 140, и замечая, что угол 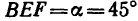
* Хотя из рассмотрения условия равновесия узла А установлено, что усилие в стержне 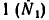
Из уравнения (7)
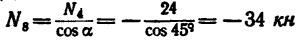
Из уравнения (8)
(стержень 7 сжат).
6. Вырежем узел В, к которому приложены четыре силы: реакции 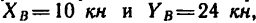

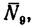
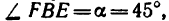
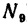
из которого
(стержень 9 растянут).
Усилия, возникающие во всех стержнях под действием внешних нагрузок, определены. Теперь_ рассмотрим узел F. Вырезав этот узел и составив для сил 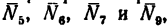
Найденные значения усилий в стержнях целесообразно представить в виде таблицы:
Задача №9
Определить усилия в стержнях 4, 5 и 6 фермы, нагруженной тремя силами: 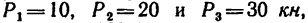
Решение.
1. Так же как и при решении методом вырезания узлов, прежде всего определяем реакции опор; в данном случае они те же, что и в предыдущем примере:
2. Разрежем ферму через стержни 4, 5 и 6 и, отбросив правую ее часть, заменим действие правой части на левую силами 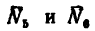
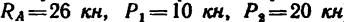
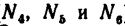
3. Составим три уравнения равновесия:
Из уравнения (1)
(стержень 5 растянут).
Из уравнения (2)
(стержень 6 растянут).
Из уравнения (3)
(стержень 4 сжат).
Сравнивая найденные числовые значения усилий в 4, 5 и 6 стержнях фермы с теми, которые для этих же стержней получены в задаче 103-17, видим, что они одинаковы.
Правильность решения здесь можно проверить, составив уравнение проекций сил на ось х. Для проверки это уравнение вполне надежно, так как в него входят все три искомые силы. Проверку решения этим способом рекомендуется произвести самостоятельно.
- Заказать решение задач по теоретической механике
Ферма и аналитические методы расчета
Постановка задачи:
Плоская ферма опирается на неподвижный и подвижный шарниры. К узлам фермы приложены нагрузки. Найти усилия в стержнях фермы методом Риттера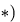
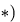
Эта задача является усложненным вариантом задачи, где усилия в стержнях можно было легко определить только из уравнений проекций, не находя реакции опор и не привлекая понятие момента силы. Аналогично можно поступить и в этой задаче, однако порядок системы линейных уравнений, описывающей равновесие всех узлов, будет велик, поэтому, во-первых, надежно решить такую систему можно только с помощью компьютера, во-вторых, таким образом будет проделана лишняя работа, так как система уравнений содержит усилия всех стержней, в том числе и тех, которые по условию задачи не требуется определять. Поэтому для решения сложных ферм, содержащих большое число стержней, применим метод Риттера, основная идея которого — независимое определение усилий в стержнях. Эту же идею можно с успехом применять и в других задачах статики.
План решения:
1. Освобождаем ферму от внешних связей. Действие опорных шарниров заменяем их реакциями. Для определения реакций опор составляем три уравнения равновесия.
2. Проверяем найденные реакции, составляя еще одно уравнение равновесия фермы.
3. В тех стержнях, где это возможно, усилия находим методом Риттера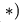
Рассматриваем равновесие одной из частей фермы (как правило, где меньше нагрузок). Для стержней, усилия в которых необходимо определить, находим точки Риттера (моментные точки). Они являются точками попарного пересечения линий действия сил в рассеченных стержнях. Искомые усилия определяем из уравнений моментов рассматриваемой части относительно точек Риттера.
Если два стержня в сечении параллельны, то точки Риттера для третьего стержня не существует, и для определения усилия в нем необходимо составить уравнение проекций на ось, перпендикулярную параллельным стержням.
В уравнение метода Риттера всегда входит усилие только одного стержня. Это позволяет искать усилия независимо одно от другого,
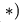
уменьшая тем самым возможность ошибок и избегая накопления неизбежных погрешностей округления в численных расчетах.
4. Определяем усилия методом вырезания узлов. Этот метод применяют в тех случаях, когда сечения Риттера для нужного стержня не существует. Вырезаем узел фермы, к которому подходит стержень с искомым усилием. Выбираем оси и составляем уравнения равновесия узла в проекциях. Решаем уравнения относительно искомого усилия. Если к узлу подходит более двух стержней с неизвестными усилиями, то метод вырезания узлов можно комбинировать с методом Риттера.
Задача №10
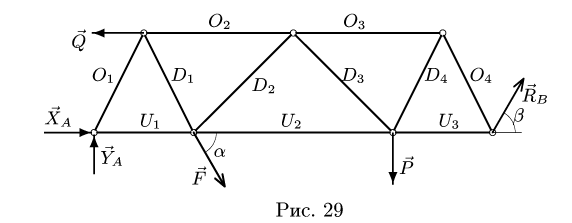
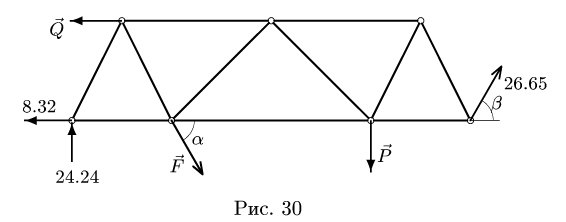
Плоская ферма опирается на неподвижный и подвижный шарниры (рис. 22). К узлам фермы приложены две вертикальные нагрузки Р — 90 кН и две наклонные 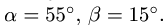
Решение
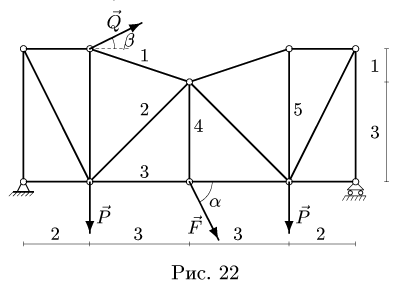
1. Освобождаем ферму от внешних связей. Действие опор заменяем их реакциями. Левую (неподвижную) шарнирную опору заменяем двумя составляющими реакции 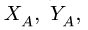
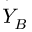
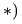
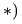
Система уравнений состоит из трех независимых друг от друга уравнений, решение которых легко найти, подставив численные значения нагрузок и углов из условия
2. Проверяем найденные вертикальные реакции, составляя уравнение проекций всех сил на ось у:
Горизонтальную реакцию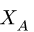
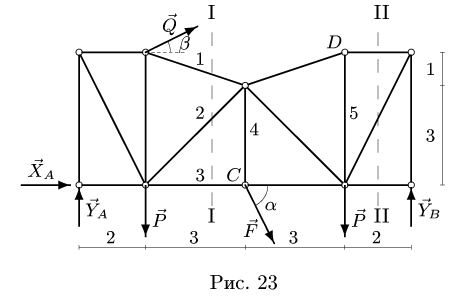
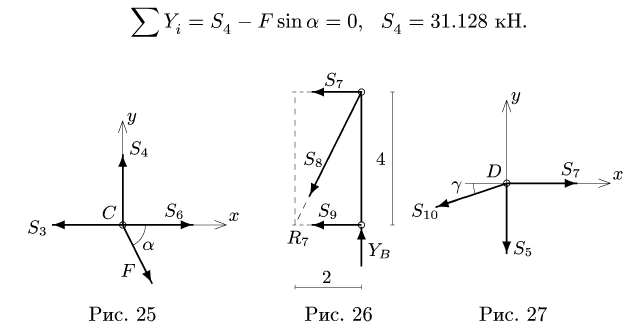
3. Методом Риттера находим усилия в стержнях 1, 2, 3. Сечением I-I (рис. 23) мысленно разделяем ферму на две части, пересекая три стержня.Действие разрезанных частей заменяем их усилиями.
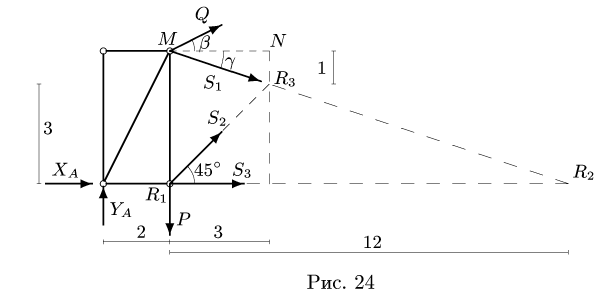
Рассматриваем левую часть (рис. 24), на которую действуют четыре известных силы 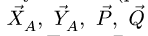
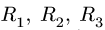
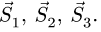
Точка 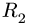
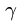
Уравнения метода Риттера имеют вид
Находим решение системы:
4. Методом вырезания узлов определяем 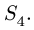
Усилие больше нуля, следовательно, стержень 4 растянут. Усилие в стержне 5 методом Риттера определить нельзя — не существует сечения, делящего ферму на две части и пересекающего при этом три стержня. В этом состоит недостаток метода. Поэтому воспользуемся методом вырезания узлов совместно с методом Риттера. Находим 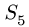
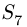
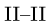
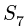
Находим 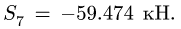
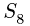
Вырезаем узел D и составляем уравнения равновесия (рис. 27):
Исключая 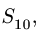
Результаты расчетов в кН занесем в таблицу:
Второе свойство имеет исключения. Существуют фермы, которые одним сечением можно разделить на две, рассекая N > 3 стержней. При этом для одного из стержней существует точка Риттера — точка пересечения остальных N — 1 стержней (подумайте, как выглядит такая ферма).
2. Сечение Риттера не обязательно должно изображаться непрерывной линией. В ферме на рис. 4, с. 15 для определения усилия в стержне АВ надо выполнить разрывное сечение (какое?). Экспериментируя с сечениями, не забывайте про три его основных свойства.
3. Рассматривая одну из частей рассеченной фермы, забудьте на время о существовании другой. Иначе в уравнения равновесия вы можете случайно включить внешние силы или реакции опор отброшенной части.
4. Не стоит беспокоиться, если точка Риттера находится на отрезанной части, располагается где-нибудь далеко или попадает на шарнир. Ее положение может быть где угодно.
5. В уравнения метода Риттера (моментов или проекций) должно войти только одно усилие стержня фермы. В этом основной смысл метода Риттера. Очень часто встречается следующая ошибка. Составляя уравнение, студент неправильно выбирает точку Риттера или составляет не то уравнение, например, уравнение проекций вместо уравнения моментов. При этом в уравнение кроме одного неизвестного усилия входят и другие, ранее найденные. В принципе такое уравнение может быть и верно, и ответ получится верным, но это не метод Риттера, где определение усилий производится независимо одно от другого во избежание накопления ошибок.
6. Положение точки Риттера для каждого стержня не зависит от рассматриваемой части. Однако степень сложности уравнения моментов для разных частей фермы может существенно отличаться. Для большей надежности решения уравнение Риттера (в форме уравнения моментов или уравнения проекций) для одной части может служить проверочным для другой.
7. Проверить расчет можно на компьютере.
Ферма и графический расчет
Постановка задачи:
С помощью диаграммы Максвелла-Кремоны найти усилил в стержнях фермы.
План решения:
Графический метод расчета ферм является дополнением к аналитическим методам расчета, которые вы изучили в предыдущем параграфе. Диаграмма Максвелла-Кремоны состоит из отдельных силовых многоугольников. Каждый многоугольник соответствует равновесию какого-либо узла фермы.
1. Обозначаем усилия в стержнях фермы.
2. Освобождаем ферму от связей. Действие опор заменяем их реакциями. Составляем три уравнения равновесия. Находим реакции.
3. Проверяем найденные реакции, составляя еще одно уравнение равновесия.
4. Изображаем все силы, действующие на ферму (включая найденные аналитически реакции опор), в виде векторов вне фермы. Если реакция опоры отрицательная, то заменяем ее направление на противоположное. Для графического способа требуются только реальные направления реакций.
5. Обозначаем буквами или цифрами внешние поля — области чертежа, разделенные силами и стержнями фермы.
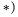
6. Обозначаем буквами или цифрами внутренние поля — области, ограниченные стержнями фермы.
7. Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям.
8. Построение диаграммы Максвелла-Кремоны начинаем с многоугольника внешних сил. Выберем направление обхода фермы (по часовой стрелке или против). Начинаем с произвольной силы. Откладывая ее в масштабе и соблюдая направление, обозначаем на диаграмме начальную и конечную точку строчными буквами, соответствующими ее новому обозначению по направлению обхода. Следующая сила пристраивается к концу первой и т.д. до замыкания многоугольника внешних сил и реакций опор.
9. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены точки двух соседних с ней полей.
Таким образом, начинать графический расчет можно с поля, у которого имеется два соседних с ним внешних поля, уже отмеченные на диаграмме. Искомая точка лежит на пересечении прямых, параллельных стержням, имена которых состоят из имени искомой точки и точек найденных внешних полей. Этот пункт выполняем многократно, до полного построения диаграммы. Модули усилий в стержнях равны длинам соответствующих отрезков на диаграмме.
10. Определяем знаки усилий. Рассматриваем шарнир фермы, к которому подходит какая-либо внешняя нагрузка или стержень с усилием известного знака. Равновесие шарнира изображено на диаграмме замкнутым силовым многоугольником с заданным направлением обхода. Сопоставляя направление усилия на диаграмме и его направление в вырезанном узле, определяем знак усилия. Если направление вектора на многоугольнике совпадает с направлением вектора, приложенного к узлу, то усилие больше нуля. В противном случае — усилие меньше нуля, т.е. стержень сжат.
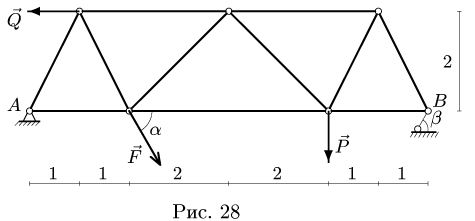
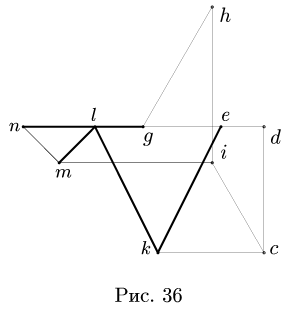
Задача №11
С помощью диаграммы Максвелла-Кремоны найти усилия в стержнях фермы (рис. 28).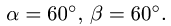
Решение
1. Обозначаем усилия в стержнях фермы так, как это принято в строительной механике. Усилия в стержнях верхнего пояса (слева направо) — 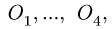
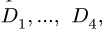
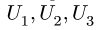
2. Определяем реакции опор фермы. Реакцию 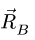
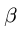
Решаем уравнения и получаем следующие значения:
3. Проверяем вертикальные реакции, составляя уравнение проекций на вертикальную ось:
4. Изображаем все силы, действующие на ферму. Реакцию 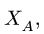
5. Обозначаем внешние поля — области чертежа, разделенные силами и стержнями фермы, — 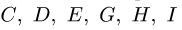
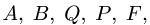
6. Обозначаем внутренние поля 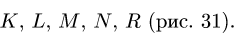
7. Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям. Приведем таблицу соответствия имен.
8. Строим многоугольник внешних сил. Выберем направление обхода фермы по часовой стрелке. Начинаем с произвольной силы, например, F = 20 кН. Откладывая в масштабе эту силу и соблюдая ее направление, обозначаем начальную и конечную точку строчными буквами г и с, соответствующими направлению обхода — из поля I в поле С. Следующая по часовой стрелке нагрузка — вертикальная реакция опоры 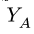
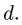
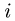
9. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены два соседних с ним поля. Таким образом, начинать графический расчет можно с поля у которого соседние поля Н и G определены на диаграмме, или К с известными соседними полями Е и С (рис. 31). Рассматриваем поле К. По направлению стержней ЕК и КС проводим линии через точки ей с диаграммы. Точка их пересечения — 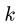
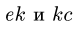
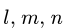
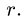
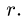
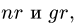
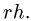
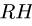
10. Определяем знаки усилий. Рассмотрим, например, усилие Ох. Вырезаем узел А, к которому приложено усилие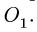
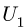
Здесь обход cdek против часовой стрелки задает реакция опоры 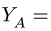
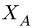
Если направление вектора на многоугольнике совпадает с направлением вектора, приложенного к узлу, то усилие больше нуля — стержень растянут. В противном случае — усилие 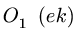
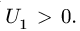
Окончательные результаты в кН заносим в таблицу:
- Замечание 1. Точность, с которой можно получить усилия графическим способом, обычно невысока. Результаты с тремя знаками после запятой, данные в таблицах, получены, конечно, не графически, а из решения задачи аналитическим методом вырезания узлов
.
- Замечание 2. Графический способ расчета ферм в реальной инженерной практике безнадежно устарел, для расчета пространственных ферм он вообще не годится. Однако в учебных целях, для проверки аналитического решения и как пример изящного и быстрого определения усилий с помощью карандаша и линейки, диаграмма Максвелла-Кремоны сохраняет свое значение.
- Замечание 3. В качестве необычной задачи программирования, предлагаем попробовать найти алгоритм автоматического построения диаграммы Максвелла-Кремоны в системе Maple V, Maple 7, Mathematics 4 или в любом другом пакете, позволяющем работать с графикой. Основное требование к программе — не составлять уравнения равновесия узлов фермы в проекциях. Допустимо найти аналитическим методом реакции опор.
Пространственная ферма
Постановка Задачи. Определить усилия е стержнях пространственной фермы, нагруженной в одном узле силами.
План решения:
Задача является естественным обобщением задачи § 1.1, с. 14, в которой методом вырезания узлов определялись усилия в простейшей плоской ферме. Этот же метод применим и здесь, единственное отличие — вместо двух уравнений равновесия узла в проекциях на оси в пространственной задаче будет три уравнения.
1. Узлы фермы находятся в равновесии. Вырезаем узлы, заменяя действие стержней их реакциями. Реакцию незагруженного стержня направляем вдоль его оси. Используя правило знаков, согласно которому усилие растянутого стержня считается положительным, реакцию каждого стержня направляем из шарнира по направлению внешней нормали сечения стержня. Расчет начинаем с узла, к которому подходят три стержня с неизвестными усилиями.
2. Для каждого из шарниров составляем по три уравнения равновесия в проекциях. Решаем полученную систему.
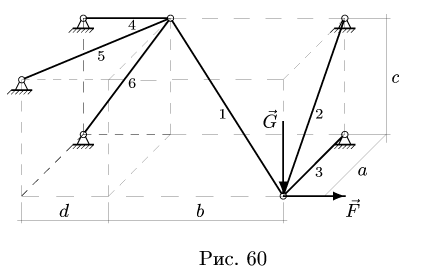
Задача №12
Найти усилия в стержнях 1-6 пространственной фермы, нагруженной в одном узле вертикальной силой G = 100 кН и горизонтальной F = 40 кН. Даны размеры а = 12 м, b = 16 м, с = 10 м, d = 5 м (рис. 60).
Решение
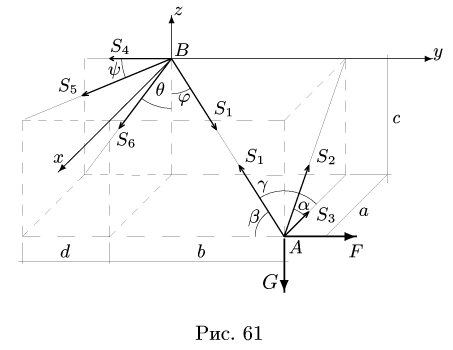
1. Узлы А и В находятся в равновесии. Вырезаем эти узлы, заменяя действие стержней их реакциями, направленными из узла к стержню(рис 61.)
Стержень 1 является общим для обоих узлов, поэтому на рисунке есть два противоположно направленных вектора с усилием 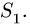
2. Расчет начинаем с узла А, к которому подходят три стержня с неизвестными усилиями. Составляем уравнения равновесия узла в проекциях на три оси координат:
Система уравнений (1) содержит три неизвестных усилия
Вычисляем тригонометрические функции, входящие в уравнения.
Решение системы (1):
Знаки найденных усилий показывают, что стержни 1 и 2 растянуты, а стержень 3 сжат. Составляем уравнения равновесия узла В:
Уравнения (2) содержат три неизвестных усилия 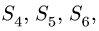
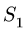
Решение системы (2):
Знаки найденных усилий показывают, что стержни 5 и 6 сжаты, а стержень 4 растянут.
Результаты расчета (в кН) заносим в таблицу:
- Пространственная система сходящихся сил
- Момент силы относительно точки и относительно оси
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Параллельные силы
- Произвольная плоская система сил
- Равновесие системы, состоящей из нескольких тел
- Графостатика в теоретической механике
Задача 1. Построить эпюры Q и M в балке с шарниром.
1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть левую часть, то в уравнении будут присутствовать две неизвестные RА и МА. Значит, следует рассмотреть правую часть (из него найдем RВ).
Теперь из него найдем МА
Следующее уравнение из него найдем RА
2. Строим эпюру Q.
Участок первый — АС, смотрим левую часть
Участок второй — СВ, смотрим правую часть
3. Строим эпюру М
Определим момент в точке, где Q=0 (момент имеет экстремум), это момент в точке К, т.е. МК , для этого определим положение точки К.
Это уравнение первого участка, на котором находится точка К
в точке К
Строим эпюры. Задача решена.
Задача 2. Построить эпюры Q и M в балке с шарниром.
1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть правую часть, то в уравнении будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.
Знак «-» говорит о том, что реакция RВ направлена в обратную сторону.
Проверка:
2. Построение эпюры Q.
Участок первый — ЕА, смотрим левую часть
Участок второй — АС, смотрим левую часть
Участок третий — СВ, смотрим левую часть
Участок четвертый — ВД, смотрим правую часть
3. Построение эпюры М
Т.к. точки экстремума на эп.Q не наблюдается, определяем изгибающий момент в середине участка ВД
Строим эпюры, задача решена.


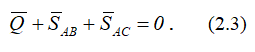
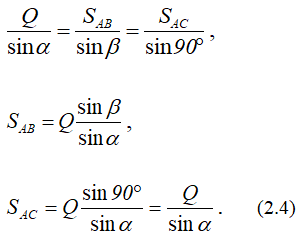
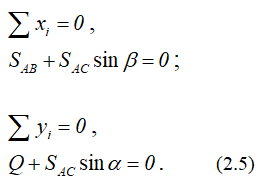
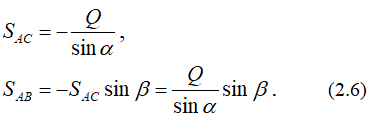




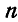
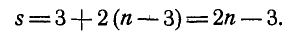
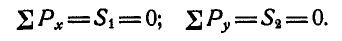
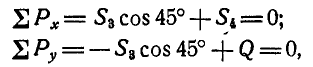
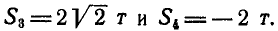
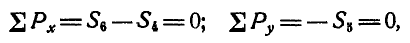
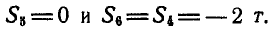

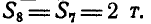
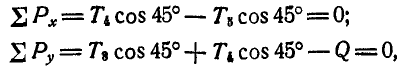
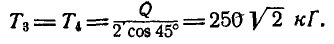
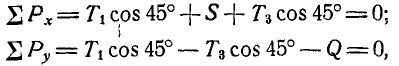
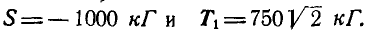
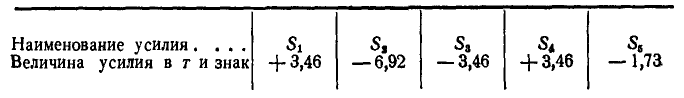
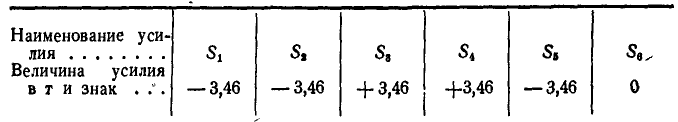
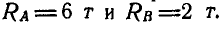
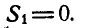
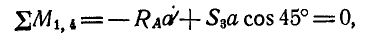
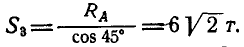
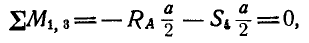
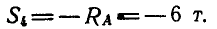
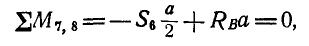
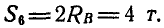

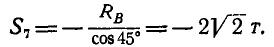
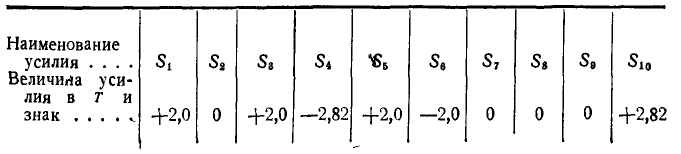
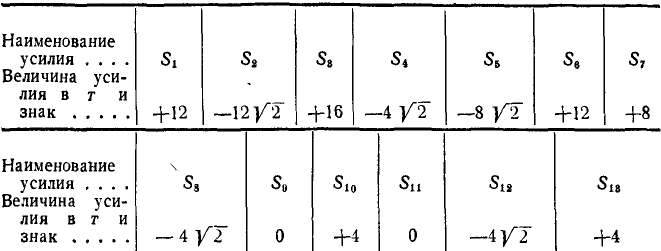
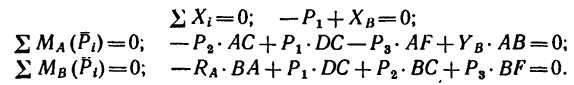
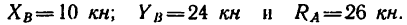
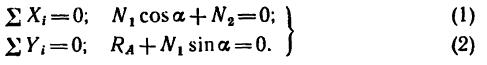
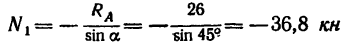
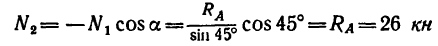
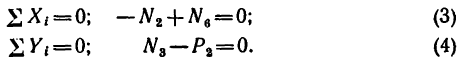
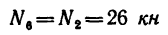
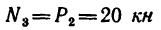
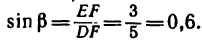
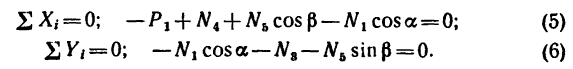
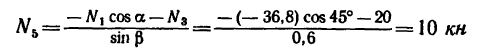
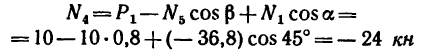
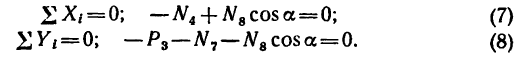
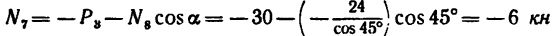
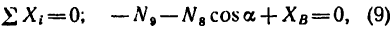
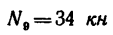

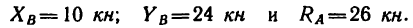
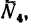
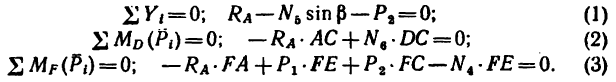
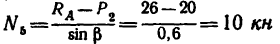
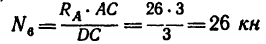
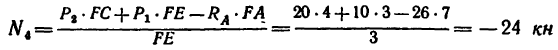
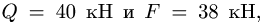
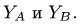
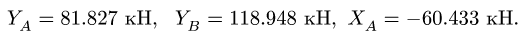
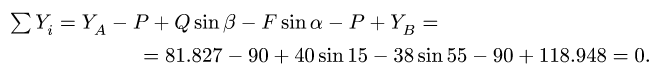
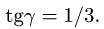
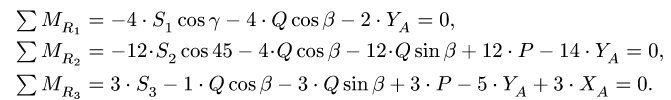
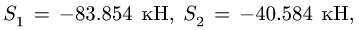
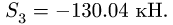
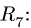
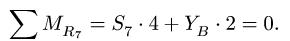
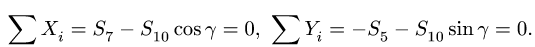
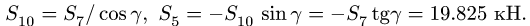

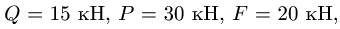
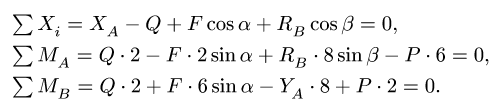
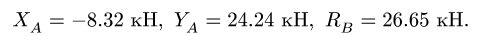
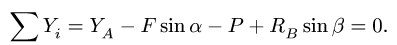
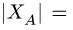


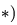 .
.