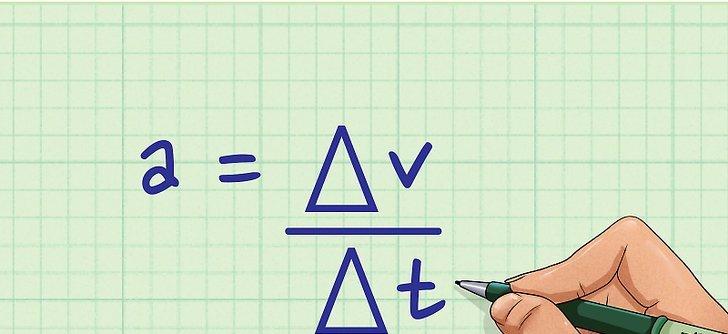Как найти ускорение через уравнение движения тела - Исправление недочетов и поиск решений вместе с Examum.ru

Формулы вычисления ускорения через скорость. Пример задачи

Любое перемещение тел изучает специальный раздел физики — кинематика. В нем не рассматриваются причины, которые привели к началу движения тела, а изучаются лишь законы изменения положения тела в пространстве с течением времени. В данной статье ответим на вопрос, как найти ускорение через скорость.

Скорость и ускорение — основные кинематические характеристики

Вам будет интересно: Идиолект — это. Общие сведения, место и роль

Каждый школьник сможет дать ответ на вопрос, что такое скорость. Под ней понимают физическую величину, которая определяет быстроту прохождения телом расстояний, что математически выражается через производную пути l по времени t:

В системе СИ скорость принято измерять в метрах в секунду (м/с).

Если взять теперь производную по времени t от скорости v, то мы получим ускорение a:

a = dv/dt = d2l/dt2.

Заметим, что ускорение может быть также рассчитано, как вторая производная по времени от пути. Величина a показывает быстроту, с которой изменяется величина v. Как правило, ускорение определяют в метрах в секунду в квадрате (м/с2).

Величины a и v являются векторными. Скорость направлена по касательной к траектории, а ускорение совпадает с вектором изменения скорости.

Равноускоренное (равнозамедленное) движение по прямой

Когда тело движется вдоль прямой линии с постоянным ускорением, то есть a=const, то существует всего три формулы определения ускорения через скорость и время:

Первое выражение позволяет определить ускорение, если тело начало ускоренное движение из состояния покоя. Оно отличается от математического определения ускорения тем, что в данном случае определяется средняя величина a за время движения t. Второе выражение также справедливо для ускоренного движения, только в этом случае до возникновения ускорения тело уже имело скорость v0. Наконец, третья формула применяется тогда, когда тело замедляет свое движение (тормозит) с постоянным ускорением.

Отметим, что все три равенства предполагают линейную зависимость между величинами a и v.

Пример решения задачи

Автомобиль двигался по трассе со скоростью 80 км/ч. Затем он начал тормозить и остановился ровно через 1 минуту. Необходимо определить его среднее ускорение торможения.

Прежде чем пользоваться записанной в предыдущем пункте формулой ускорения через скорость, переведем известные из условия задачи величины в единицы СИ:

v0 = 80 км/ч = 22,22 м/с;

Поскольку автомобиль в итоге остановился, то v = 0. Подставим все известные значения в соответствующую формулу, получим:

a = (v0-v)/t = 22,22/60 = 0,37 м/с2.

Рассчитанная величина не является слишком большой по сравнению с ускорением, которое наша планета сообщает всем телам (9,81 м/с2).

Механическое движение

О чем эта статья:

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

тело отсчета
система координат
часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

Время — в международной системе единиц СИ измеряется в секундах [с].
Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

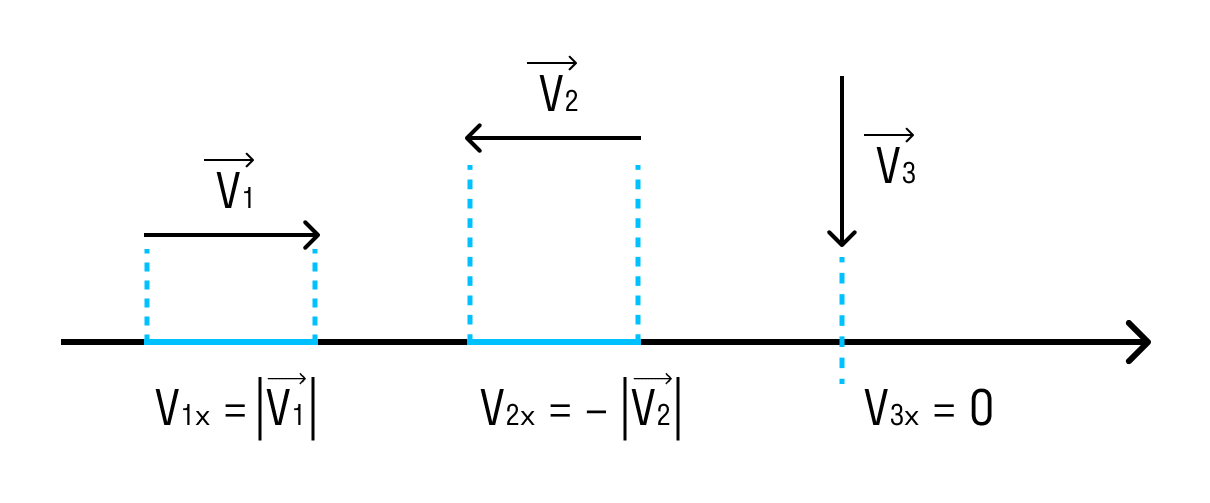
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Физика. Ускорение, масса, сила

Ускорение это изменение скорости в единицу времени.
a = V / t
Ускорение в физике это не основная физическая величина, а производная.
Преобразуем: V = S / t тогда : a = S / t 2
именно это дает запись формулы ускорения в основных величинах и единицу измерения ускорения : метры на секунды в квадрате.

Таким образом: ускорение есть там, где есть линейная скорость движения и эта скорость — меняется в числовом значении.
Но у скорости есть еще направление.
И физики не смогли это дело оставить так, чтобы не запутать и сказали: раз скорость векторная величина, пусть будет так, что ускорение возникает и при изменении направления.
Так ускорение появляется при равномерном круговом движении?
Для нас ясность тут очень важна, так как это траектория движения планет.
Как так, спрашиваем мы, скорость движения постоянна, а появилось ускорение?
Это же нонсенс!

Предлагается:1. чтобы исключить двойное толкование, принять ускорение, как только изменение линейной скорости в единицу времени.
Далее»
2.Основным написанием формулы ускорения считать a = S / t 2,
а написание a = V / t — производным. И еще точнее, чтобы убрать квадратную функцию времени (чего не существует) a = S1- S2 / t. Т.е. ускорение это разница (изменение) пройденного пути в единицу времени. И всё!

3. Считать ускорение не физической, а математической величиной, употребимой в узких пределах.
4. Определение «изменение направления» к ускорению не применять. Считать ускорением только изменение величины, а не направления.

Где мы в формулах встречаем ускорение?
Формула силы. По второму закону Ньютона F = m х a означает, что, если к массе m приложить силу F , то тело будет двигаться с скоростью, которая имеет ускорение а. И чтобы вычислить ускорение, нам надо замерить путь и время, так зачем же оно? Только для облегчения записи вычислений.
Ускорение со знаком плюс означает только то, что за одну единицу времени тело будет проходить все более меньший путь.
В случае со свободным падением тела используется понятие ускорение свободного падения тела (без учета сопротивления воздуха) g

И формула пишется F = m х g. Но эта формула справедлива только для случая, когда есть состояние свободного падения. Если тело неподвижно относительно центра Земли, то эта формула не используется, так как приводит к ошибке.
Например. Тело массой m (1 кг.) лежит на весах.
Что показывают весы? Они показывают массу в 1 кг.
А не вес, как силу притяжения ( m х g).
Тело давит на опору весов, с силой притяжения, а по Закону Всемирного тяготения
сила тяжести m х M / R2 ускорения свободного падения не содержит и вес показывают только массу. Таким образом, если задать задачу: арбуз массой m положили на весы и спросили какой вес? А потом перемножить m х g получим неверный результат, потому что весы показывают значение массы, а ускорения g
здесь вообще нет.

Напишите такое уравнение:

m х g = m х M / R2 и получите, после сокращения массы g = M / R2
и эта формула хороша только тем, что объясняет почему ускорение свободного падения не зависит от массы тела , а зависит только от массы Земли и радиуса в квадрате.

Но математически эта формула выглядит как неверная, так как не совпадают единицы измерения.
Наши ученые тут опять отличились. Они ввели гравитационную постоянную и G дали ей единицу измерения м3·с;2·кг;1 (ответ сошелся) а вопрос остался:
Есть от чего сойти с ума : во втором законе ускорение от массы зависит, а при свободном падении — нет!
А происходит это от того, что при увеличении массы силя притяжения растет, а ускорение по второму закону уменьшается и результирующая остается неизменной от массы.

Вообще, вес это еще одна производная от действия гравитации величина, которая в уважающих себя учебниках физики не рассматривается, но очень важна на базаре.

Рассмотрим случай невесомости, когда вес исчезает. Например, парашютист прыгает
с самолета, а парашют дома забыл. (сопротивление воздуха не учитываем, как всегда, зачем ему теперь воздух нужен) Скорость растет соразмерно с величиной 9.8 метров пройденного пути в секунду!
И здесь появляется еще один парадокс: сила гравитации есть, масса есть, ускорение. тоже есть, а давления на опору (как рыночного понятия веса) нет!

А, если есть сопротивление воздуха?
Тогда: F = m х (g — а)
Здесь а это то реальное ускорение, которое возникает и оно меньше ускорения свободного падения. И, если оно равно g — сила давление опору ( или вес ) равен нулю.

источники:

http://skysmart.ru/articles/physics/mehanicheskoe-dvizhenie

http://proza.ru/2015/09/27/1494

Источник

Ускорение скорость, с которой скорость изменения. Поскольку скорость является векторной величиной, ускорение также является векторной величиной. В результате требуется не только направление, но и величина. Итак, в этой статье мы рассмотрим, как определить величину ускорения.

Мы используем формулы и соотношения для расчета величины. Мы можем представить величину в единицах. Поскольку ускорение определяется как изменение скорости во времени, единицей СИ для него является ㎨. На ускорение влияют различные факторы, такие как скорость, время, сила и т. Д. Мы рассмотрим несколько различных методов оценки величины ускорения. Давайте читать дальше.

1. Как найти величину ускорения из определения ускорения:

Как мы все знаем, ускорение относится к скорости изменения скорости. Если начальная скорость тела равна vi, а его конечная скорость равна vf, ускорение можно вычислить, разделив изменение скорости на временной интервал Δt:

Как определить величину ускорения

(Здесь величина вектора показана жирным шрифтом, а вертикальные линии обозначают величину вектора или, можно сказать, абсолютное значение вектора, которое всегда положительно.)

Используя скорость и время, приведенное выше уравнение можно использовать для определения величины ускорения.

2. Как определить величину ускорения Из второго закона Ньютона:

Второй закон Ньютона гласит, что сила получается умножением ускорения на массу тела. Итак, как можно определить величину ускорения?

Итак, согласно второму закону Ньютона, сила, действующая на тело, пропорциональна его ускорению, тогда как масса обратно пропорциональна ускорению. Переведем эти утверждения в формулу величины ускорения:

Это визуализированная форма уравнения. Вы не можете редактировать это напрямую. Щелчок правой кнопкой мыши даст вам возможность сохранить изображение, и в большинстве браузеров вы можете перетащить изображение на свой рабочий стол или в другую программу.

Таким образом,

3. Как найти величину ускорения по компонентам вектора ускорения:

Как мы все знаем, ускорение — это векторная величина. Чтобы получить это количество, сложите компоненты ускорения. Здесь можно использовать простое правило сложения векторов. Если задействованы две компоненты вектора, мы можем написать:

В декартовой плоскости мы можем использовать координаты X и Y. Как в этих обстоятельствах определить величину ускорения? В декартовой системе координат компоненты X и Y перпендикулярны друг другу. Величину ускорения можно вычислить, возведя значения в квадрат и затем вычислив квадратный корень из суммы.

В результате уравнение выглядит следующим образом:

Формула величины ускорения в трехмерном пространстве:

4. Как найти величину центростремительного ускорения:

Из-за непрерывного изменения направления при круговом движении скорость изменяется, что приводит к ускорению. Ускорение направлено в направлении центра круга. Возведение в квадрат скорости тела v и деление ее на расстояние тела от центра круга дает величину центростремительного ускорения. Таким образом, центростремительное ускорение:

Уравнения движения — это, по сути, уравнения, которые объясняют движение любой физической системы и демонстрируют взаимосвязь между перемещением объекта, скоростью, ускорением и временем.

Когда величина ускорения постоянна, кинематическое уравнение движения в одном измерении также используется для вычисления величины ускорения.

Ниже приведены уравнения движения:

Когда мы рассматриваем ускорение в уравнении, мы получаем следующее:

Вот как мы можем определить величину ускорения.

Решенные примеры определения величины ускорения:

1 задачи:

Автомобиль трогается с места и развивает скорость 54 км / ч за 3 секунды. Найти его ускорение?

Решение: Автомобиль заводится с отдыха. Таким образом, начальная скорость автомобиля

Vi = 0 м / с

Vf = 54 км / ч

= (54 ✕ 1000) / 3600

= 15 м / с

Δt = 3 с

Таким образом, Ускорение : a = (Vf — Vi) / Δt

= (15-0) / 3

2 задачи:

Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.

Решение: Приложенная сила F = 12 Н

Масса объекта m1 = 3 кг

m2 = 6 кг

Ускорение объекта массой 3 кг

а1 = F / м1

= 12 / 3

Ускорение объекта массой 6 кг

а2 = F / м2

= 12 / 6

Поскольку масса и ускорение обратно пропорциональны, мы можем наблюдать, что по мере увеличения массы ускорение уменьшается.

3 задачи:

Тело движется по оси абсцисс в соответствии с соотношением

, где x в метрах, а t в секундах. Найти ускорение тела при t = 3 с.

Решение: Вот :

t = 3 с

Скорость v = dX / dt

= d / dt ()

= -2 + 6т

Ускорение : a = dv / dt

= d / dt (-2 + 6t)

Как мы видим, для этого движения ускорение не зависит от времени; ускорение будет постоянным на протяжении всего движения, а величина ускорения будет .

4 задачи:

Рассчитайте центростремительное ускорение точки на расстоянии 7.50 см от оси ультрацентрифуги, вращающейся при число оборотов в минуту.

Решение: Здесь нам даны:

Расстояние от центра r = 7.5 см

= 0.0750 м

Угловая скорость

Теперь

= 589 м / с

Таким образом, центростремительное ускорение:

Источник

Загрузить PDF

Ускорение характеризует быстроту изменения скорости движущегося тела.^[1] Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. ^[2] Ускорение измеряется в метрах в секунду за секунду (м/с²) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.

1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.^[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с².
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.^[4] Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = v_к — v_н и Δt = t_к — t_н, где v_к – конечная скорость, v_н – начальная скорость, t_к – конечное время, t_н – начальное время.^[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что t_н = 0.
3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (v_к — v_н)/(t_к — t_н). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v_к — v_н)/(t_к — t_н)
  - Напишите переменные: v_к = 46,1 м/с, v_н = 18,5 м/с, t_к = 2,47 с, t_н = 0 с.
  - Вычисление: a = (46,1 — 18,5)/2,47 = 11,17 м/с².
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v_к — v_н)/(t_к — t_н)
  - Напишите переменные: v_к = 0 м/с, v_н = 22,4 м/с, t_к = 2,55 с, t_н = 0 с.
  - Вычисление: а = (0 — 22,4)/2,55 = -8,78 м/с².
Реклама

1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.^[6] Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
- Второй закон Ньютона описывается формулой: F_рез = m x a, где F_рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с²).
2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.^[7] Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.
- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с².^[8]
4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с²
Реклама

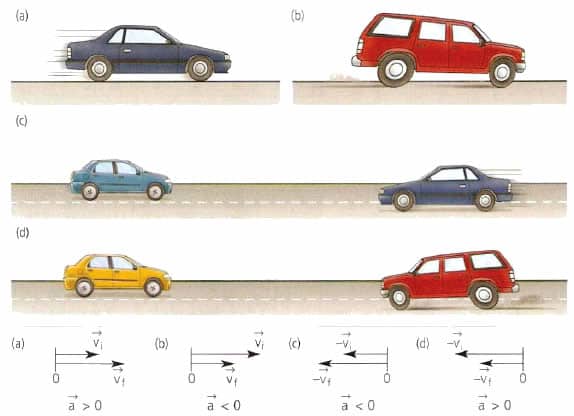
Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:

Движение автомобиля	Изменение скорости	Значение и направление ускорения
Движется вправо (+) и ускоряется	+ → ++ (более положительное)	Положительное
Движется вправо (+) и замедляется	++ → + (менее положительное)	Отрицательное
Движется влево (-) и ускоряется	— → — (более отрицательное)	Отрицательное
Движется влево (-) и замедляется	— → — (менее отрицательное)	Положительное
Движется с постоянной скоростью	Не меняется	Равно 0

2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с². Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с².
3

Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):

Реклама

Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 — 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с².

Об этой статье

Эту страницу просматривали 190 271 раз.

Была ли эта статья полезной?

Источник

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь — x нулевое- начальная координата. v нулевое — начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Как найти ускорение — определение и формулы расчета в физике

Содержание:

Что такое ускорение
- Единица измерения
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
Мгновенное ускорение
Максимальное ускорение
Среднее ускорение
Проекция ускорения

Что такое ускорение

Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.

Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.

Единица измерения

В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как рассчитать ускорение: формулы

Для прямолинейного движения

Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.

В этом случае ускорение находится по следующим формулам:

(a;=;frac{mathrm V}t)

(a;=;frac{2S}{t^2})

(a;=;frac{V^2}{2S})

Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V₀ и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

(overrightarrow a=frac{overrightarrow F}m)

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.

Выражается по формуле:

( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})

Максимальное ускорение

(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.

Среднее ускорение

Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.

Проекция ускорения

Определение проекции ускорения на ось (х):

(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.

Насколько полезной была для вас статья?

Рейтинг: 1.92 (Голосов: 36)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник