1. Тела в начальном состоянии движутся друг относительно друга
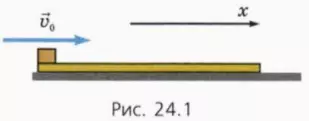
Пусть на гладком столе лежит доска длиной L и массой mд. На краю доски находится небольшой брусок массой mб (рис. 24.1). Коэффициент трения между бруском и доской μ. В начальный момент доска покоится, а бруску толчком сообщают начальную скорость 
Как будут двигаться тела?
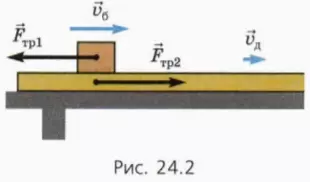
При скольжении бруска по доске на него и на доску действуют противоположно направленные равные по модулю силы трения скольжения 

Возможны два варианта дальнейшего развития событий:
1) брусок будет скользить по доске, пока их скорости не станут равными, то есть пока брусок не остановится относительно доски. Начиная с этого момента силы трения перестанут действовать на доску и брусок, и они будут скользить по гладкому столу вместе как единое целое с постоянной конечной скоростью 
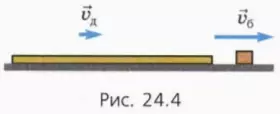
2) скорости бруска и доски не успеют сравняться до того момента, когда брусок дойдёт до противоположного конца доски. В таком случае брусок соскользнёт с доски, после чего они будут двигаться по столу с различными скоростями 

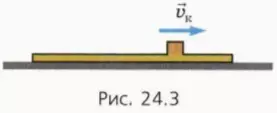
Рассмотрим сначала случай, когда доска с бруском будут двигаться как единое целое (см. рис. 24.3), и выведем условие, при котором этот случай реализуется.
? 1. Как зависят от времени проекции скорости бруска и доски на ось x, показанную на рисунке 24.1?
? 2. Через какой промежуток времени доска и брусок будут двигаться как единое целое?
? 3. Чему будет равна скорость доски с бруском, когда они будут двигаться как единое целое?
Найдём теперь условие того, что брусок будет скользить по доске до тех пор, пока их скорости не сравняются.
Так произойдёт, если путь l, пройденный бруском относительно доски, не превышает длины доски L. Путь l мы найдём, определив ускорение бруска относительно доски.
? 4. Чему равно ускорение бруска относительно доски?
? 5. Чему равен путь l, пройденный бруском относительно доски до того момента. когда их скорости сравнялись?
? 6. При выполнении какого условия доска и брусок будут двигаться как единое целое?
Рассмотрим конкретный пример.
? 7. Небольшой брусок массой 200 г находится на краю доски массой 1 кг, лежащей на гладком столе. Коэффициент трения между доской и бруском 0,5. В начальный момент скорость бруска 2,4 м/с, а доска покоится. Через некоторое время брусок и доска стали двигаться как единое целое.
а) С каким ускорением относительно доски двигался брусок?
б) Сколько времени брусок двигался по доске?
в) Какова минимально возможная длина доски?
г) Чему равна скорость доски с бруском, когда они движутся как единое целое?
Пусть теперь условие того, что доска и брусок станут двигаться как единое целое, не выполнено. Тогда брусок соскользнёт с доски, и скорость каждого тела при дальнейшем скольжении по столу останется такой, какой она была в момент соскальзывания бруска.
Чтобы найти конечные скорости бруска и доски, можно поступить, например, так.
1) Зная длину доски L, начальную скорость бруска v0 и ускорение бруска относительна доски, найдём время tск, в течение которого брусок будет скользить по доске.
2) Зная время tск, найдём скорости бруска и доски в момент соскальзывания бруска с доски. С этими скоростями они и будут скользить далее по столу.
Воспользуйтесь этими советами при выполнении следующего задания.
? 8. Небольшой брусок массой 400 г находится на краю доски длиной 1 м и массой 800 г, лежащей на гладком столе (рис. 24.1). Коэффициент трения между доской и бруском 0,2. В начальный момент скорость бруска 3 м/с, а доска покоится.
а) С каким по модулю ускорением движется брусок относительно доски?
б) Какой должна была бы быть длина доски, чтобы скорость бруска относительно доски стала равной нулю?
в) Сколько времени брусок движется по доске согласно условию задания?
г) Чему равна скорость бруска относительно стола в тот момент, когда брусок соскользнёт с доски?
д) Какой путь пройдёт доска относительно стола до того момента, когда брусок соскользнёт с доски?
2. Тела в начальном состоянии покоятся друг относительно друга
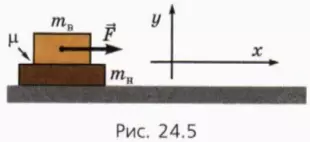
На гладком столе лежат один на другом два бруска (рис. 24.5). Массу нижнего бруска обозначим mн‚ в массу верхнего — mв. Коэффициент трения между брусками μ.
К верхнему бруску прикладывают горизонтально направленную вправо силу 
Самое главное в таких задачах — увидеть две возможности:
1) бруски могут начать двигаться друг относительно друга — тогда между ними будут действовать силы трения скольжения;
2) бруски могут начать двигаться как единое целое — тогда между ними будут действовать силы трения покоя.
Начнём с первой возможности: в таком случае модуль силы трения скольжения, действующей на каждое тело, равен μmвg. Модуль же силы трения покоя заранее неизвестен.
? 9. Объясните, почему в случае, когда верхний брусок скользит по нижнему, их ускорения относительно стола выражаются формулами
Учтём теперь, что сила 
? 10. Объясните, почему бруски будут двигаться друг относительно друга, если
? 11.На столе стоит тележка массой 500 г, а на ней лежит кирпич массой 2,5 кг. Коэффициент трения между кирпичом и тележкой 0,5, трением между тележкой и столом можно пренебречь. С какой горизонтальной силой надо тянуть кирпич, чтобы стащить его с тележки?
Итак, чтобы стащить тяжёлый кирпич со сравнительно лёгкой тележки, надо приложить к нему горизонтальную силу, которая в несколько раз превышает вес кирпича!
? 12. Объясните, почему тела движутся как единое целое, если
? 13. Объясните, почему, когда бруски движутся как единое целое, их (общее) ускорение а и модуль действующей на каждый брусок силы трения покоя Fтр.пок выражаются формулами
Рассмотрим теперь пример, когда горизонтальная сила приложена к нижнему бруску.
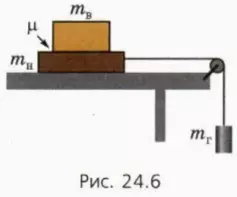
Пусть на гладком горизонтальном столе лежит брусок массой mн, а на нём — брусок массой mв (рис. 24.6). Коэффициент трения между брусками μ. К нижнему бруску привязана лёгкая нерастяжимая нить, переброшеивая через блок, а к нити подвешен груз массой mг. Как будут двигаться тела?
В этой ситуации тоже есть две возможности:
1) бруски могут начать двигаться друг относительно друга;
2) бруски могут начать двигаться как единое целое.
На этот раз проще начать со второй возможности, потому что, когда бруски движутся как единое целое, мы можем рассматривать систему, состоящую только из двух тел — объединённого бруска массой M = mв + mн и груза массой mг.
? 14. С каким ускорением движутся бруски как единое целое?
? 15. С каким максимально возможным ускорением могут двигаться бруски как единое целое?
Подсказка. Ускорение верхнему бруску сообщает сила трения покоя, которая не превышает силу трения скольжения.
? 16. Объясните, почему бруски движутся как единое целое, если выполнено соотношение
Если это соотношение не выполнено. то бруски будут двигаться порознь. Ускорение верхнему бруску сообщает в таком случае сила трения скольжения, равная по модулю μmвg. Такая же по модулю, но противоположно направленная сила трения скольжения действует на нижний брусок.
? 17. Каковы ускорения брусков, если они движутся друг относительно друга?
? 18. На гладком горизонтальном столе лежит брусок массой mн = 0,5 кг, а на нём — другой брусок массой mв = 0,3 кг (см. рис. 24.6). К нижнему бруску привязана лёгкая нерастяжимая нить, переброшенная через блок, и к нити подвешен груз массой mг = 0,2 кг. В начальный момент бруски покоятся.
а) При каком наименьшем коэффициенте трения μmin между брусками они будут двигаться как единое целое?
б) С каким ускорением (ускорениями) движутся бруски при коэффициенте трения между ними 0,5?
в) С каким ускорением (ускорениями) движутся бруски, если коэффициент трения между ними равен 0,1?
Дополнительные вопросы и задания
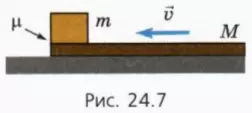
19. На гладком столе лежит доска длиной l и массой M. На одном конце доски находится небольшой брусок массой m (рис. 24.7). Коэффициент трения между бруском и доской μ. В начальный момент тела покоятся. Какую наименьшую скорость надо толчком сообщить доске, чтобы она выскользнула из-под бруска?
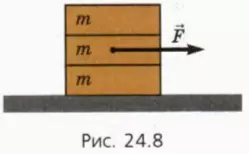
20. На гладком столе лежат один на другом три одинаковых бруска массой m = 100 г каждый (рис. 24.8). Коэффициент трения между брусками μ = 0,2. К среднему бруску приложена горизонтально направленная сила 
а) С каким максимально возможным ускорением может двигаться верхний брусок?
б) С каким максимально возможным ускорением может двигаться нижний брусок?
в) При каких значениях силы F все бруски будут двигаться как единое целое?
You should upgrade or use an alternative browser.
-
Forums
-
Physics
-
Classical Physics
-
Mechanics
How can I find the acceleration of the plank
-
Thread starter
kash25 -
Start date
Dec 17, 2008 -
-
Tags -
Acceleration
-
- Dec 17, 2008
- #1
If I have a plank (mass M) resting on two identical parallel cylinders (mass m, radius R) and I pull the plank with a horizontal force F (no slipping between cylinders and floor nor between plank and cylinders), what happens? How can I find the acceleration of the plank and the rolling cylinders? Why DOESN’T a = F/M give the acceleration of the plank AND the tangential acceleration of the cylinders?
Thank you!
Answers and Replies
- Dec 17, 2008
- #2
If I’m right here, you need to consider the system as a whole. That means in f=ma, you need to be using the total translational inertia of the system, rather than just the component masses. So of course the masses are present, but as the cylinders are rolling you need to convert their moment of inertia to translational inertia by using I/R², so a = F/(M+2m+2I/R²). Where I is the moment of inertia of the rollers, which for a cylinder is mR²/2, so this conveniently reduces to a=F/(M+3m).
Unless I’m mistaken, this should give the acceleration of both the plank, and the tangential acceleration of the cylinders.
- Dec 17, 2008
- #3
I’m afraid you are.
If I have a plank (mass M) resting on two identical parallel cylinders (mass m, radius R) and I pull the plank with a horizontal force F (no slipping between cylinders and floor nor between plank and cylinders), what happens? How can I find the acceleration of the plank and the rolling cylinders?
Analyze the problem in the usual manner. Start by identifying the forces acting on the plank and the cylinders. (F is not the only force!) Draw free body diagrams for each object.
Apply Newton’s 2nd law for translation and rotation to plank and cylinders. (How does the acceleration of the plank relate to the acceleration of the cylinders?)
Why DOESN’T a = F/M give the acceleration of the plank AND the tangential acceleration of the cylinders?
Why should it? To find the acceleration of the plank (or any object) you need the net force acting on it. Besides the applied force F, what other forces act on the plank?
- Dec 18, 2008
- #4
Ah yes, I’m thinking as if the plank was connected to the cylinders as if they were axles, in the situation described the plank would eventually roll off the top of the cylinders as they would only be traveling half as fast?
Actually I’ve also assumed that the cylinders are on the ground, but as the OP said rolling and not rotating, I’m hoping that was a correct assumption to make.
Although you are correct, for the cylinders to roll, there must be friction between the cylinders and the plank, and the ground.
My excuse is I was tired. :p
Suggested for: How can I find the acceleration of the plank
- May 19, 2022
- Aug 27, 2021
- Jan 8, 2022
- Jul 15, 2021
- Mar 9, 2022
- Aug 7, 2021
- Dec 29, 2020
- Jan 17, 2022
- Jan 15, 2021
- Mar 21, 2020
-
Forums
-
Physics
-
Classical Physics
-
Mechanics
2020-04-04
На гладкой горизонтальной поверхности лежит доска длиной $L$ и массой $M$. На краю доски покоится небольшой брусок. На брусок начинает действовать постоянная горизонтальная сила так, что он движется вдоль доски с ускорением, которое больше ускорения доски. Найдите ускорение, с которым двигалась доска, если за время движения по ней бруска выделилось количество теплоты $Q$.
Решение:
Пусть $m$ — масса бруска, $a$ — искомое ускорение доски, $ka$ — ускорение бруска $(k > 1)$, $F$ — постоянная сила, действующая на брусок, $F_{тр}$ — сила трения между доской и бруском. Запишем второй закон Ньютона для бруска и для доски в проекции на горизонтальную ось:
$F — F_{тр} = mka$,
$F_{тр} = Ma$.
Если $t$ — время движения бруска от одного края доски до другого, то в лабораторной системе отсчета путь, пройденный бруском, равен $L_{m} = frac{kat^{2}}{2}$, а путь, пройденный доской, равен $L_{M} = frac{at^{2}}{2}$. Разность этих путей есть длина доски:
$L = L_{m} — L_{M}$.
Работа силы, приложенной к бруску, равна
$A = FL_{m} = (mka + Ma)L_{m}$.
Закон сохранения энергии для системы брусок + доска имеет вид
$A = frac{m}{2} (kat)^{2} + frac{M}{2} (at)^{2} + Q = mkaL_{m} + MaL_{m} + Q$.
Отсюда получим
$Q = Ma (L_{m} — L_{M} ) = MaL$, и $a = frac{Q}{ML}$.
Комментарии
Опубликовано 20 декабря, 2009 — 23:48 пользователем yago
Cила, с которой брусок действует на доску, — это сила трения, которая равна ?mg, так как масса доски в 2 раза больше массы бруска + масса самого бруска, так как он на доске F = 3ma.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 11:09 пользователем Alexandr Ыых
yago, это в том случае, если бы коэффициент трения был указан между столом и доской. Так как коэффициент трения доски о стол не указан, а написано «гладкой поверхности», то, вероятно, имеется в виду, что он равен нулю.
Сила, действующая на доску со стороны бруска:
F ≤ ?mg.
Ускорение доски:
a ≤ F / M = g? (m / M).
a ≤ 10 × 0.5 × (1/2) = 2.5 (m / s2).
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 11:59 пользователем yago
Тогда получается, что брусок не имеет массы?
Нет трения, но силу притяжения земли никто не отменял. Брусок действует на доску с силой N = mg, и доска действует на стол с силой N = 2mg + N (бруска).
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 13:34 пользователем klaas
Alexandr, скажите, пожалуйста, доска приходит в движение под действием силы трения, возникающей между бруском и доской? А сила трения доски о стол равна нулю?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 16:04 пользователем Fizik-999
Доска приходит в движение под действием силы трения между бруском и доской.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 17:23 пользователем klaas
А не может здесь участвовать ещё одна сила, которая приложена либо к бруску, либо к доске?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 19:06 пользователем AssemblerIA64
Alexandr Ыых, по-моему, у Вас должно быть равенство, т.к. это сила трения скольжения, а не покоя. А так всё правильно :).
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 20:01 пользователем Ruleeezzz
Cила трения между бруском и доской будет доске придавать ускорение. k — коэффициент трения.
kmg = Ma,
kmg = 2ma,
kg = 2a,
a = kg / 2.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 22:48 пользователем Alexandr Ыых
Если бы в задаче спрашивалась «какое максимальное ускорение», то я бы написал равенство. А просто «какое ускорение» может быть любым, от нуля до максимального. Поэтому неравенство.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 21 декабря, 2009 — 23:36 пользователем yago
Делить надо на 3, а не на два. Это можно понять из закона сохранения импульса. Представьте, что тело когда-нибудь остановится, и двигаться будет только доска.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 22 декабря, 2009 — 10:42 пользователем Alexandr Ыых
AssemblerIA64 в Декабрь 21, 2009 — 19:06.
Alexandr Ыых, по-моему, у Вас должно быть равенство, т.к. это сила трения скольжения, а не покоя.
Да. Вы правы. Извините, у меня после прочтения задачи в голове неправильно отложилось, что доска скользит, а брусок на ней лежит. А так как брусок скользит по доске, то действительно речь идет о максимальном ускорении, и нужен знак равенства.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 22 декабря, 2009 — 10:43 пользователем Alexandr Ыых
yago в Декабрь 21, 2009 — 23:36.
Делить надо на 3, а не на два.
У меня складывается впечатление, что Вы и я по-разному представляем, что за процессы описаны в задачке. Не могли бы Вы записать формулами, как из закона сохранения импульса следует, что делить надо на три?
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Опубликовано 22 декабря, 2009 — 21:42 пользователем zvv48
Ответ:
a2 = kg / 2 — ускорение доски;
a1 = −kg — ускорение бруска.
Источник:
Савченко О.Я., «Задачи по физике», 1988 г. Задача № 2.1.30, б.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Сообщения без ответов | Активные темы | Избранное
|
|
Механика. Осн. динамики. Несколько непонятна задача
|
|
02/01/23 |
Брусок массой
|
|
|
|
|
sergey zhukov |
Re: Механика. Осн. динамики. Несколько непонятна задача
|
|
17/10/16 |
В ответе получил ускорение бруска относительно доски. Почему же относительно доски? Полученное ускорение бруска — относительно плоской поверхности. Чтобы получить ускорение относительно доски, нужно вычесть из него ускорение доски. Вы же рассматриваете баланс сил на брусок в инерциальной системе отсчета. В неинерциальной системе отсчета (ускоряющаяся доска) в балансе сил должны появиться силы инерции, а у вас же их нет. Если вести расчет в системе доски и учитывать силы инерции — получите ускорение относительно доски. Если в задаче специально не оговаривается, то нужно искать ускорение в инерциальной системе отсчета. Решение правильное.
|
|
|
|
|
WinterPrimat |
Re: Механика. Осн. динамики. Несколько непонятна задача
|
|
02/01/23 |
sergey zhukov Спасибо. Похоже, мне еще много часов нужно потратить, чтоб набить руку)
|
|
|
|
|
EUgeneUS |
Re: Механика. Осн. динамики. Несколько непонятна задача
|
|
11/12/16 |
WinterPrimat А в пособии нет каких-то указаний, как нужно округлять значения в ответах, до какого значащего знака?
|
|
|
|
|
WinterPrimat |
Re: Механика. Осн. динамики. Несколько непонятна задача
|
|
02/01/23 |
|
|
|
|
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |

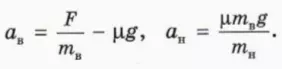
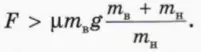
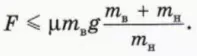
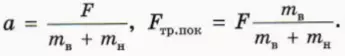
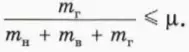

 лежит на доске массой
лежит на доске массой  , которая лежит на гладкой поверхности (горизонтальной, полагаю).
, которая лежит на гладкой поверхности (горизонтальной, полагаю). .
. (горизонтально, полагаю)?
(горизонтально, полагаю)?
 , на которое действует сила
, на которое действует сила  . Тогда:
. Тогда:
 )
)



 )
) . Посему не уверен, правильно ли вообще рассуждал.
. Посему не уверен, правильно ли вообще рассуждал.