Как найти ускорение груза формула

Печатается по решению кафедры общей физики: протокол № 3 от 27 декабря 2012 г.

Составители: к.ф.-м.н., доц. Акманова Г.Р. асс. Шафеев Р.Р.

Лабораторная работа № 2 ИЗУЧЕНИЕ ЗАКОНОВ КИНЕМАТИКИ И ДИНАМИКИ

ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА НА МАШИНЕ АТВУДА

Приборы и принадлежности: установка ФМ 11 (машина Атвуда),

блок электронный, набор грузов. Цель работы: 1. Изучение законов кинематики и динамики

равноускоренного поступательного движения.

2.Экспериментальное определение ускорения движения.

3.Определение теоретического значения ускорения движения.

КРАТКАЯ ТЕОРИЯ

Механическое движение – простейшая форма материи, которое состоит в перемещении тел или их частей относительно друг друга в пространстве с течением времени. В общем случае движение тел или их частей может иметь довольно сложный характер. Для того, чтобы задать движение тела, нужно сначала изучить законы движения отдельных частиц тела. Любое тело можно представить как систему материальных точек. В механике применяется абстракция реального тела – абсолютно твердое тело (или просто твердое тело). Абсолютно твердым называется тело, в котором отдельные части не перемещаются друг относительно друга, т.е. абсолютно твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно (тело не деформируется).

Любое сложное движение твердого тела сводится к простым движениям: поступательному и вращательному. Поступательным называется такое движение тела, при котором любая прямая, проведенная в теле, сохраняет свое направление неизменным пространстве. При поступательном движении все точки твердого тела описывают одинаковые траектории и имеют одинаковые перемещения, скорости и ускорения. Поэтому для задания поступательного движения твердого тела достаточно знать законы движения одной его точки (центра масс).

либо декартовы координаты x, y, z как функция t:

Уравнения (1) и (2) называются кинематическими уравнениями движения тела (точки). В случае равнопеременного движения вдоль оси x (y=0,z=0) уравнение (2) для x имеет вид:

где 0 — начальная скорость тела,

а — ускорение.

Если 0 =0, то (3) переходит в

(4)

Уравнение динамики движения записывается на основании второго закона Ньютона: «Изменение импульса тела пропорциональна движущей силы и происходит по направлению той прямой, по которой эта сила действует»:

Fdt — импульс силы. Из (5) получим

В виде (5) и (6) второй закон Ньютона справедлив и в релятивистской механике. Если m=const, то (6) примет вид:

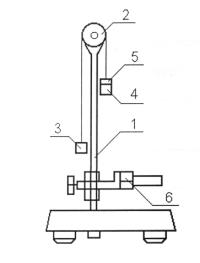
Для определения характера движения и изучения зависимости ускорения системы грузов от их масс используется машина Атвуда (рис. 1). Она состоит из укрепленного на штативе 1 шкива 2 радиуса R, через который перекинута нить с подвешенными на ней одинаковыми грузами 3 и 4. Масса этих грузов может быть увеличена добавочными небольшими грузами (перегрузками) 5.

Рис.1. Машина Атвуда

Система приводится в движение за счет добавочного груза 5 массой m0. Шкив 2 вращается вокруг оси с малым трением, т. е. можно считать, что движение грузов равнопеременное. Ускорение грузов определяют

2

t2

Ускорение грузов:

a R 2 R t2

Ускорение a, путь S и время движения t при равнопеременном движении связаны соотношением:

При таком движении ускорение постоянно a=const и не зависит от пути S. Таким образом, если при равнопеременном движении груза шкив совершает один полный оборот ( =2 ) за время t1, два полных оборота ( =4 ) за время t2, то из выражения (9) следует критерий равнопеременности движения:

Найдем закон движения грузов. Обозначим через m — массу груза 3. Тогда масса груза 4 с добавочным грузом 5 есть величина, равная m + m0. На правый груз действуют две силы: сила тяжести (m +m0)g и сила натяжения нити T4. Их равнодействующая вызывает движение груза с ускорением а. По второму закону Ньютона сила F, действующая на правый груз, равна произведению массы m на ускорение а:

Результирующая сила равна векторной суммесил, действующих на

платформу: F Fi .

Проектируя вектор сил и вектор ускорения на осьОХ получаем:

m m0 a m m0 g T4 (13)

где g = 9,8 м/с2 – ускорение свободного падения тела.

Если предположить, что нить нерастяжима, то ускорение груза 3 равно (-a). Тогда для груза 3 получим:

Из второго закона Ньютона вытекают два следствия. Если на тело постоянной массы m действовать различными силами F1 и F2, то согласно второму закону Ньютона, тело будет двигаться с разными ускорениями a1 и a2, отношение которых равно отношению сил:

при m=const.

Из уравнения (12) следует, что если к телам с различными массами m1 и m2 приложить равные силы, то тела будут двигаться с разными ускорениями a1 и a2, отношение, которых обратно пропорционально отношению масс:

при F =const.

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Экспериментальная установка — машина Атвуда представлена на рис.1.Основание снабжено тремя регулируемыми опорами и зажимом для фиксации вертикальной стойки. Вертикальная стойка выполнена из металлической трубы, на которую нанесена миллиметровая шкала, и имеет визир.

На верхнем кронштейне размещается узел подшипников с малоинерционным шкивом, через который перекинута капроновая нить с двумя основными грузами и набором разновесов, электромагнитный тормоз, предназначенный для фиксации исходного положения грузов. Нижний кронштейн имеет зажим для крепления на вертикальной стойке и элементы фиксации фотодатчика. Установка работает от блока электронного.

Для проведения измерений необходимо перекинуть через блок 2 нить с двумя грузами 3 и 4 и убедиться, что система находится в положении безразличного равновесия. Установить кронштейн с фотодатчиком 6 в нижней части шкалы вертикальной стойки, а фотодатчик расположить таким образом, чтобы правый груз при движении вниз проходил в центре рабочего окна фотодатчика (за нижнее положение груза берется риска шкалы, соответствующая риске на корпусе фотодатчика и являющаяся как бы продолжением оптической оси фотодатчика, которую пересекает движущийся груз).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Упражнение 1.

Экспериментальное определение ускорения движения

1.Нажать кнопку «СЕТЬ», находящуюся на задней панели блока электронного.

2.Установить правый груз в крайнем верхнем положении.

3.Положить на правый груз один из добавочных грузов 5 массой

10 г.

4.Нажать на кнопку «ПУСК » блока. Происходит растормаживание электромагнита, правый груз начинает опускаться, и таймер блока

начинает отсчет времени. При пересечении правым грузом оптической оси фотодатчика отсчет времени прекратится.

Записать показания таймера, т. е. время движения грузов.

5.Определить по шкале пройденный грузом путь S, как расстояние от нижней плоскости груза (в верхнем положении) до оптической оси фотодатчика.

6.Не меняя первоначальной высоты груза, повторить опыт 5 раз. Найти среднее время движения t.

7.Определить значение ускорения движения груза по формуле:

2S

aэксп. t2 .

8. Определить ускорение свободного падения по формуле:

g aэксп. 2m m0 , m0

где m = 50 г – масса основного груза, m0 – масса добавочного груза.

9.Оценить относительные и абсолютные погрешности величин ускорения a и ускорения свободного падения g.

10.Повторить измерения и вычисления согласно пп. 3 – 9 с добавочным грузом массой 20 г.

Упражнение 2.

Определение теоретического значения ускорения

1.Определить теоретическое значение ускорения движения груза по формуле:

2.Сравнить теоретическое и экспериментальное значения ускорения движения груза.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Дайте определение механического движения. Какое движение называется поступательным? Вращательным?

2.Какое тело называется абсолютно твердым?

3.Дайте определения физических понятий: системы отсчёта,

радиусавектора, скорости, ускорения.

4.Какое движение называется равноускоренным? Каким образом связаны между собой путь, время и скорость прямолинейного равноускоренного движения?

5.Сформулируйте и запишите второй закон Ньютона. Какие следствия вытекают из второго закона Ньютона.

6.В каких системах отсчета справедливы законы Ньютона?

7.Что характеризует масса тела?

8.Каким образом из экспериментальных данных определяется ускорение движения грузов?

9.Как изменится ускорение системы, если увеличить массу основного груза m , не меняя массы перегрузка?

ЛИТЕРАТУРА

1.Стрелков С.П. Механика. — СПб: Изд-во «Лань», 2005, § 2-11, 16-21.

2.Сивухин Д.В. Общий курс физики. Т.1. Механика, — М: ФИЗМАТЛИТ; Изд-во МФТИ, 2006, § 2-4, 9-12.

3.Савельев И.В. Курс общей физики. Кн.1. Механика.- СПб: Изд-во

«Лань», 2007,§ 1.1-1.5, 2.2 – 2.6.

4.Иродов И.Е. Механика. Основныезаконы. – М.:БИНОМ.

ЛабораторияЗнаний, 2010, §1.1 -1.3, 2.1– 2.4.

Чему равно ускорение груза массой 500 кг, который опускают с помощью троса, если сила натяжения троса 4000 Н? Сопротивлением воздуха пренебречь.

Найти ускорение тела, разгоняющегося за 10 с от 5 до 100 км/ч.

В начальный момент времени тело двигалось со скоростью

$v_{0} = frac{5000}{3600} approx 1,39 м/с.$

Скорость в конце интервала:

$v_{1} = frac{100000}{3600} approx 27,8 м/с.$

Подставив числовые значения в формулу, получаем:

$a = frac{v_1 — v_0}{t}$

$a = frac{27,8 — 1,39}{10} approx 2,64 м/с^{2}$

Ответ: ускорение составило $ 2,64 м/с^{2}$