Как найти ускорение по 3 силами - Исправление недочетов и поиск решений вместе с Examum.ru

Download Article

If you’ve ever watched a bright red Ferrari fly ahead of your Honda Civic after a stoplight, you’ve experienced differing rates of acceleration firsthand. Acceleration is the rate of change in the velocity of an object as it moves. You can calculate this rate of acceleration, measured in meters per second, based on the time it takes you to go from one velocity to another, or based on the mass of an object.^[1]

1
Define Newton’s Second Law of Motion. Newton’s second law of motion states that when the forces acting on an object are unbalanced, the object will accelerate. This acceleration is dependent upon the net forces that act upon the object and the object’s mass.^[2] Using this law, acceleration can be calculated when a known force is acting on an object of known mass.
- Newton’s law can be represented by the equation F_net = m x a, where F_net is the total force acting on the object, m is the object’s mass, and a is the acceleration of the object.
- When using this equation, keep your units in the metric system. Use kilograms (kg) for mass, newtons (N) for force, and meters per second squared (m/s²) for acceleration.
2
Find the mass of your object. To find the mass of an object, simply place it on a balance or scale and find its mass in grams. If you have a very large object, you may need to find a reference that can provide you with the mass.^[3] Larger objects will likely have a mass with the unit of kilograms (kg).
- For this equation, you will want to convert the mass into kilograms. If the mass you have is in grams simply divide that mass by 1000 to convert to kilograms.
Advertisement
3
Calculate the net force acting on your object. A net force is an unbalanced force. If you have two forces opposing each other and one is larger than the other, you will have a net force in the direction of the larger force.^[4] Acceleration happens when an unbalanced force acts on an object, causing it to change speeds towards the direction the force is pushing or pulling it.
- For example: Let’s say you and your big brother are playing tug-of-war. You pull the rope to the left with a force of 5 newtons while your brother pulls the rope in the opposite direction with a force of 7 newtons. The net force on the rope is 2 newtons to the right, in the direction of your brother.
- In order to properly understand the units, know that 1 newton (N) is equal to 1 kilogram X meter/second squared (kg X m/s²).^[5]
4
Rearrange the equation F = ma to solve for acceleration. You can change this formula around to solve for acceleration by dividing both sides by the mass, so: a = F/m.^[6] To find the acceleration, simply divide the force by the mass of the object being accelerated.
- Force is directly proportional to the acceleration, meaning that a greater force will lead to a greater acceleration.
- Mass is inversely proportional to acceleration, meaning that with a greater mass, the acceleration will decrease.
5
Use the formula to solve for acceleration. Acceleration is equal to the net force acting on an object divided by the mass of the object. Once you’ve established the values for your variables, do the simple division to find the acceleration of the object.
- For example: A 10 Newton force acts uniformly on a mass of 2 kilograms. What is the object’s acceleration?
- a = F/m = 10/2 = 5 m/s²

1
Define the equation for average acceleration. You can calculate the average acceleration of an object over a period of time based on its velocity (its speed traveling in a specific direction), before and after that time. To do this you need to know equation for acceleration: a = Δv / Δt where a is acceleration, Δv is the change in velocity, and Δt is the amount of time it took for that change to occur.^[7]
- The unit for acceleration is meters per second per second or m/s².^[8]
- Acceleration is a vector quantity, meaning it has both a magnitude and a direction.^[9] The magnitude is the total amount of acceleration whereas the direction is the way in which the object is moving. If it is slowing down the acceleration will be negative.
2
Understand the variables. You can further define Δv and Δt: Δv = v_f — v_i and Δt = t_f — t_i where v_f is the final velocity, v_i is the initial velocity, t_f is the ending time, and t_i is the starting time.^[10]
- Because acceleration has a direction, it is important to always subtract the initial velocity from the final velocity. If you reverse them, the direction of your acceleration will be incorrect.
- Unless otherwise stated in the problem, the starting time is usually 0 seconds.
3
Use the formula to find acceleration. First write down your equation and all of the given variables. The equation is a = Δv / Δt = (v_f — v_i)/(t_f — t_i). Subtract the initial velocity from the final velocity, then divide the result by the time interval. The final result is your average acceleration over that time.
- If the final velocity is less than the initial velocity, acceleration will turn out to be a negative quantity or the rate at which an object slows down.
- Example 1: A race car accelerates uniformly from 18.5 m/s to 46.1 m/s in 2.47 seconds. What is its average acceleration?
  - Write the equation: a = Δv / Δt = (v_f — v_i)/(t_f — t_i)
  - Define the variables: v_f = 46.1 m/s, v_i = 18.5 m/s, t_f = 2.47 s, t_i = 0 s.
  - Solve: a = (46.1 – 18.5)/2.47 = 11.17 meters/second².
- Example 2: A biker traveling at 22.4 m/s comes to halt in 2.55 s after applying brakes. Find his deceleration.
  - Write the equation: a = Δv / Δt = (v_f — v_i)/(t_f — t_i)
  - Define the variables: v_f = 0 m/s, v_i = 22.4 m/s, t_f = 2.55 s, t_i = 0 s.
  - Solve: a = (0 – 22.4)/2.55 = -8.78 meters/second².

Understand the Direction of Acceleration. The physics concept of acceleration doesn’t always match how we would use the term in everyday life. Every acceleration has a direction, usually represented as positive if it’s UP or RIGHT, and negative if DOWN or LEFT. See if your answer makes sense based on this breakdown:

Behavior of a Car	How is Velocity Changing?	Direction of Acceleration
Driver moving right (+) hits gas pedal	+ → ++ (more positive)	positive
Driver moving right (+) hits brakes	++ → + (less positive)	negative
Driver moving left (-) hits gas pedal	— → — (more negative)	negative
Driver moving left (-) hits brakes	— → — (less negative)	positive
Driver moves at constant velocity	remains the same	acceleration is zero

2
Understand the Direction of Force. Remember, a force only causes acceleration in the direction of the force. Some problems may try to trick you with irrelevant values.
- Example Problem: A toy boat with mass 10kg is accelerating north at 2 m/s². A wind blowing due west exerts a force of 100 Newtons on the boat. What is the boat’s new northward acceleration?
- Solution: Because the force is perpendicular to the direction of motion, it does not have an effect on motion in that direction. The boat continues to accelerate north at 2 m/s².
3
Understand Net Force. If more than one force acts on an object, combine them into a net force before you calculate acceleration. For a problem in two dimensions, this looks something like this:
- Example Problem: April is pulling a 400 kg container right with a force of 150 newtons. Bob stand on the left of the container and pushes with a force of 200 newtons. A wind blowing left exerts a force of 10 newtons. What is the acceleration of the container?
- Solution: This problem uses tricky language to try and catch you. Draw a diagram and you’ll see the forces are 150 newtons right, 200 newtons right, and 10 newtons left. If «right» is the positive direction, the net force is 150 + 200 — 10 = 340 newtons. Acceleration = F / m = 340 newtons / 400 kg = 0.85 m/s².

Calculator, Practice Problems, and Answers

Add New Question

Question

How do you solve acceleration word problems?

Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.

Academic Tutor

Expert Answer
Question

What is the SI unit for acceleration?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

SI units are standardized units that are used internationally in scientific writing. When describing acceleration, use the SI units meters per seconds squared (m/s^2).
Question

How do you calculate acceleration without time?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

If you know that acceleration is constant, you can solve for it without time if you have the initial and final velocity of the object as well as the amount of displacement. Use the formula v^2=u^2+2as where v is the final velocity, u is the initial velocity, a is acceleration, and s is displacement. Solve for a to find acceleration.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

References

About This Article

Article SummaryX

To calculate acceleration, use the equation a = Δv / Δt, where Δv is the change in velocity, and Δt is how long it took for that change to occur. To calculate Δv, use the equation Δv = vf — vi, where vf is final velocity and vi is initial velocity. To caltulate Δt, use the equation Δt = tf — ti, where tf is the ending time and ti is the starting time. Once you’ve calculated Δv and Δt, plug them into the equation a = Δv / Δt to get the acceleration. To learn how to calculate acceleration from a force, read the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,764,253 times.

Reader Success Stories

DrDave Alpenschnee

Mar 5, 2018

«I am an Alpine ski instructor, and was interested in how unbalanced forces cause one ski to accelerate more than…» more

Did this article help you?

Источник

Загрузить PDF

Ускорение характеризует быстроту изменения скорости движущегося тела.^[1] Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. ^[2] Ускорение измеряется в метрах в секунду за секунду (м/с²) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.

1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.^[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с².
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.^[4] Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = v_к — v_н и Δt = t_к — t_н, где v_к – конечная скорость, v_н – начальная скорость, t_к – конечное время, t_н – начальное время.^[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что t_н = 0.
3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (v_к — v_н)/(t_к — t_н). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v_к — v_н)/(t_к — t_н)
  - Напишите переменные: v_к = 46,1 м/с, v_н = 18,5 м/с, t_к = 2,47 с, t_н = 0 с.
  - Вычисление: a = (46,1 — 18,5)/2,47 = 11,17 м/с².
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v_к — v_н)/(t_к — t_н)
  - Напишите переменные: v_к = 0 м/с, v_н = 22,4 м/с, t_к = 2,55 с, t_н = 0 с.
  - Вычисление: а = (0 — 22,4)/2,55 = -8,78 м/с².
Реклама

1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.^[6] Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
- Второй закон Ньютона описывается формулой: F_рез = m x a, где F_рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с²).
2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.^[7] Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.
- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с².^[8]
4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с²
Реклама

Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:

Движение автомобиля	Изменение скорости	Значение и направление ускорения
Движется вправо (+) и ускоряется	+ → ++ (более положительное)	Положительное
Движется вправо (+) и замедляется	++ → + (менее положительное)	Отрицательное
Движется влево (-) и ускоряется	— → — (более отрицательное)	Отрицательное
Движется влево (-) и замедляется	— → — (менее отрицательное)	Положительное
Движется с постоянной скоростью	Не меняется	Равно 0

2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с². Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с².
3

Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):

Реклама

Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 — 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с².

Об этой статье

Эту страницу просматривали 190 509 раз.

Была ли эта статья полезной?

Источник

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

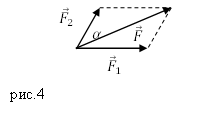
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

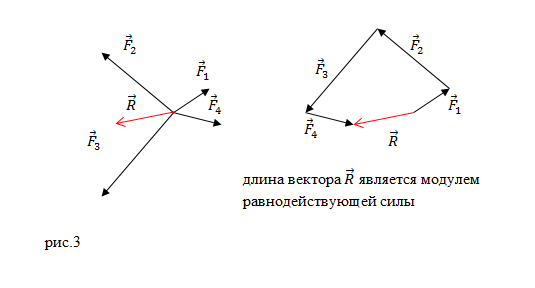
Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

направления 2 -х составляющих сил;
модуль и направление одной из составляющих сил;
модули 2 -х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

Как найти равнодействующую трех векторов

Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок). Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)

Согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением Из графика определим ускорение, которое остается постоянным на протяжении всего интервала времени:

Таким образом, равнодействующая всех сил равна

а если бы ускорение было отрицательно, то и равнодействующая была бы отрицательной?

Скорость, сила, ускорение — все это векторные величины. Правильно говорить не про их знак, а про знак проекции этих векторов на некоторую ось. Если проекция скорости уменьшается, то ускорение направлено против оси, а значит, так же направлена и равнодействующая. Следовательно, проекции этих величин отрицательны. По графику модуля скорости о знаке проекций судить нельзя. Действительно, имея только график, приведенный в условии, мы не можем сказать, ускоряется тело вдоль оси или против. Проекция ускорения может быть тут как положительной, так и отрицательной.

«Систему отсчета считать инерциальной.» Возможно ошибаюсь, ребят, но, вроде, в ИСО равнодействующая всех сил равна нулю.

ИСО — это система отсчета, в которой тело, на которое не действует никаких внешних сил, двигается равномерно и прямолинейно или покоится.

Равнодействующая сил, конечно, же может и отличаться от нуля, это, согласно второму закону Ньютона, приведет к появлению ускорения.

т.е. в инерциальной системе отсчёта нет силы трения?

и ещё: вы говорите, что тело в ИСО движется равномерно, а в условии задачи дано равноускоренное движение. так бывает?

Я не так говорю, не вырывайте слова и контекста. Я даю определение ИСО: это система отсчета, в которой тело, НА КОТОРОЕ НЕ ДЕЙСТВУЮТ ВНЕШНИЕ СИЛЫ, двигается равномерно и прямолинейно, либо покоится. А вот если СИЛЫ ДЕЙСТВУЮТ, то это приводит к появлению ускорения, о чем нам и говорит второй закон Ньютона.

Наличие силы трения определяется свойством поверхностей, а не выбором системы отсчета. И в данной задаче, она, конечно, присутствует и направлена по скорости движения автомобиля, иначе бы он просто не мог бы разгоняться. Но чему она равна, мы найти из данного графика не можем, так как есть и другие силы, например, сила сопротивления воздуха. Что мы может тут определить, так это равнодействующую всех сил. Именно ей определяется ускорение.

Пыталась найти ускорение как тангенс угла наклона касательной, то есть производную от v по t. Тут угол — 45 град, тангенс = 1, ускорение, стало быть, так же 1 м/с^2.

Подскажите пожалуйста, где в моих рассуждениях ошибка?

Ошибка в том, что тангенс надо считать, учитывая масштаб графика по осям. То есть Вы должны определить катеты прямоугольного треугольника, используя числа на осях, а потом поделить один катет на другой.

Кстати, простое доказательство, почему Ваше решение не верно. Сожмем картинку с графиком по вертикали в два раза. Угол на рисунке изменится, а ускорение, конечно, же останется прежним.

а почему считают ускорение до 8с. а не до 18, если найдем ускорение по всей длине то получается 10-0/18=1,8 и получается другой ответ!

Делить нужно на 20. Масштаб по горизонтальной оси: в одной клеточке 4 с

На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)

На рисунке обозначена равнодействующая векторов и

Поскольку модуль вектора силы равен 1 Н, заключаем, что масштаб рисунка такой, что сторона одного квадрата сетки соответствует модулю силы 1 Н. Таким образом, модуль равнодействующей равен по теореме Пифагора

А как определили эту равнодействующую трёх сил, я понять не могу?!

Чтобы найти равнодействующую, необходимо сложить вектора всех сил (например, по правилу треугольника или параллелограмма складываем вектора по два).

Если сложить вектор и вектор , получится вектор, направленный вверх длиной в одну клеточку. Теперь осталось прибавить к нему вектор . В результате и получается то, что показано красной стрелкой.

векторы F1 и F3 никак нельзя сложить правилом треугольника! дак как эту задачц решить тут решения совсем непонятные!

Когда Вы складываете параллельные вектора, у Вас просто получается «вырожденный треугольник». Правила все те же, к концу первого вектора прикладываем начало второго. Сумма векторов — это вектор, который начинается в начале первого и заканчивается в конце второго. То есть в данном случае у Вас получится вектор, направленный вверх и длиной в одну клеточку.

Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)

Силы и их равнодействующая указаны на рисунке. По теореме Пифагора, модуль равнодействующей сил равен

Под действием одной силы F₁ тело движется с ускорением 4 м/с 2 . Под действием другой силы F₂, направленной противоположно силе F₁, ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F₁ и F₂? Ответ дайте в метрах на секунду в квадрате.

Согласно второму закону Ньютона, ускорение тела пропорционально равнодействующей всех сил, действующих на него: Силы и по условию, направлены противоположно, поэтому при их одновременном действии тело будет двигаться с ускорением

Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)

Всего на тело действует три силы: сила тяжести и силы натяжения двух нитей. Поскольку тело находится в равновесии, равнодействующая всех трех сил должна равняться нулю, а значит, модуль силы тяжести равен

в условии написано,что нужно найти вес тела.

а в решении модуль силы тяжести.

Как вес может измеряться в Ньютонах.

В условии ошибка(

Вы путаете понятия массы и веса. Весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Как следует из определения, эта сила приложена даже не к телу, а к опоре. Невесомость — это состояние, когда у тела пропадает не масса, а вес, то есть тело перестает давить на другие тела.

Согласен, в решении была допущена некоторая вольность в определениях, сейчас она поправлена.

Понятие «вес тела» введен в учебную физику крайне неудачно. Если в бытовом понятии вес обозначает массу то в школьной физике, как вы правильно заметили весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Заметим, что речь идет об одной опоре и об одной нити. Если опор или нитей несколько несколько, понятие веса исчезает.

Привожу пример. Пусть в жидкости на нити подвешено тело. Оно растягивает нить и давит на жидкость с силой равной минус сила Архимеда. Почему же, говоря о весе тела в жидкости, мы не складываем эти силы, как Вы делаете в своем решении?

Я зарегистрировался на Вашем сайте, но не заметил, что же изменилось в нашем общении. Прошу извинить мою тупость, но я, будучи человеком старым, недостаточно свободно ориентируюсь на сайте.

Действительно, понятие веса тела весьма расплывчато, когда тело имеет несколько опор. Обычно вес в этом случае определяют как сумму взаимодействий со всеми опорами. При этом воздействие на газообразные и жидкие среды, как правило, исключается. Это как раз подпадает под описанный Вами пример, с подвешенным в воде грузиком.

Здесь сразу вспоминается детская задачка: «Что весит больше: килограмм пуха или килограмм свинца?» Если решать эту задачу по-честному, то нужно несомненно учитывать силу Архимеда. А под весом скорее всего мы будем понимать то, что нам будут показывать весы, то есть силу, с которой пух и свинец давят, скажем, на чашку весов. То есть здесь сила взаимодействие с воздухом как бы из понятия веса исключается.

С другой стороны, если считать, что мы откачали весь воздух и кладем на весы тело, к которому привязана веревочка. То сила тяжести будет уравновешиваться суммой силы реакции опоры и силой натяжения нити. Если мы понимаем вес как силу действия на опоры, препятствующие падению, то вес тут будет равен этой сумме силы растяжения нити и силы давления на чашку весов, то есть совпадать по величине с силой тяжести. Опять возникает вопрос: чем нитка лучше или хуже силы Архимеда?

В целом тут можно договориться до того, что понятие веса имеет смысл только в пустом пространстве, где есть только одна опора и тело. Как тут быть, это вопрос терминологии, которая, к сожалению, у каждого здесь своя, поскольку не столь уж это и важный вопрос И если силой Архимеда в воздухе во всех обычных случаях можно пренебречь, а значит, на величину веса она особо повлиять не может, то для тела в жидкости это уже критично.

Если уж быть совсем честным, то разделение сил на виды весьма условно. Представим себе ящик, который тащат по горизонтальной поверхности. Обычно говорят, что на ящик действуют две силы со стороны поверхности: сила реакции опоры, направленная вертикально, и сила трения, направленная горизонтально. Но ведь это две силы, действующие между одними и теми же телами, почему же мы просто не рисуем одну силу, являющуюся их векторной суммой (так, кстати, иногда и делается). Тут, это, наверное, вопрос удобства

Так что я немного в замешательстве, что делать с данной конкретной задачей. Проще всего, наверное, переформулировать ее и задавать вопрос про величину силы тяжести.

Не переживайте, все в порядке. При регистрации Вы должны были указать e-mail. Если теперь зайти на сайт под своим аккаунтом, то при попытке оставить комментарий в окне «Ваш e-mail» должен сразу появляться тот самый адрес. После этого система будет автоматически подписывать Ваши сообщения.

Формула модуля равнодействующей силы

На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.

Формула равнодействующей всех сил

Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.

Складывают векторы, используя правило треугольника (рис.1)

правило параллелограмма (рис.2).

или многоугольника (рис.3):

Второй закон Ньютона и формула модуля равнодействующей

Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:

$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач с решением

Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?

Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:

Вычислим модуль равнодействующей силы:

[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Нright).]

Ответ. $F=52,92$ Н

Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?

Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:

Следовательно, модуль силы можно найти как:

Ускорение точки будем искать, используя связь между ним и перемещением точки:

Первая производная от $s$ по времени равна:

Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:

Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:

источники:

http://phys-ege.sdamgia.ru/test?theme=206

http://www.webmath.ru/poleznoe/fizika/fizika_134_formula_modulja_ravnodejstvujushhej_sily.php

Источник

Задачи на Движение
под действием нескольких сил с решениями

Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам по теме «ЗАДАЧИ на Движение под действием нескольких сил с решениями»

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Автомобиль массой 5 т трогается с места с ускорением 0,6 м/с². Найти силу тяги, если коэффициент сопротивления движению равен 0,04.

ОТВЕТ: F_тяг = 5 кН.

РЕШЕНИЕ:

Задача № 2.
Определить, пользуясь графиком, как движется поезд и какова сила тяги локомотива, если известно, что масса поезда 2500 т, а коэффициент сопротивления 0,025.

ОТВЕТ: Поезд движется равнозамедленно с ускорением 0,2 м/с². F_тяги = 125 кН.