Как найти ускорение по формуле перемещения

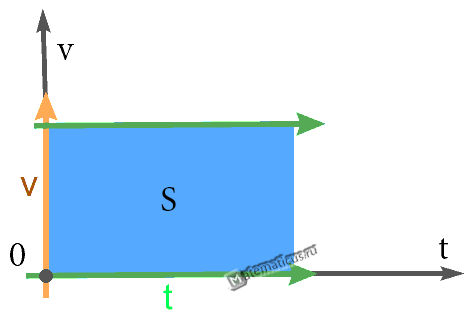
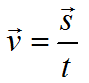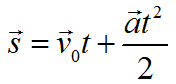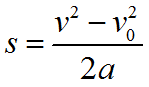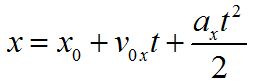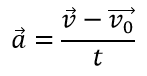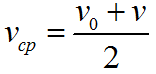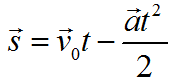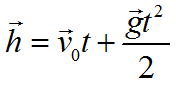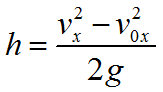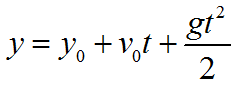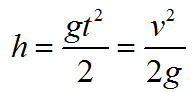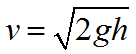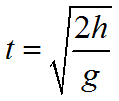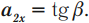Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения

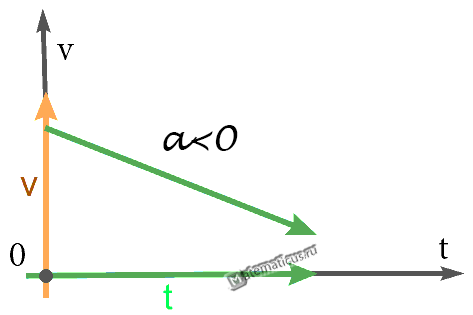
Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀ ± at

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁ оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

v = at₂

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁ = 0)

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Алиса Никитина | Просмотров: 25.5k

Кинематика — это специальный раздел теоретической механики. Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.

Кинематика — описание

Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.

Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:

1. Путь, который преодолевает тело, существенно больше, чем его размеры.
2. Расстояние между телами значительно превышает их размеры.
3. Объект совершает поступательное движение.

Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.

Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.

Теория и формулы

Благодаря многолетним исследованиям в области кинематики ученым удалось вывести определенные закономерности движения тела. С помощью справедливых уравнений представляется возможным ответить на многие вопросы о разных характеристиках, которые изменяются либо остаются постоянными во время движения объектов.

Путь, время, скорость

Расстояние представляет собой удаленность одной точки положения тела от другой. Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.

Скорость представляет собой путь, который тело преодолело в течение единицы времени. В качестве единицы времени часто используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения. В случае, когда в условиях задачи расстояние измеряется в метрах, а время пути — в секундах, то скорость следует рассчитывать в метрах в секунду (м/с). Для обозначения скорости используют латинскую букву (v).

Нередко требуется определить время пути. Данный параметр обозначают с помощью латинской буквы (t).

Важно отметить, что скорость, путь и время взаимосвязаны. При известных характеристиках скорости и времени можно определить расстояние, которое преодолело тело. Путь в данном случае равен произведению скорости и времени, рассчитывается по формуле:

(s=vtimes t)

При известных величинах времени и расстояния достаточно просто определить скорость движения тела, руководствуясь следующим уравнением:

(v=frac{s}{t})

Равномерное движение

Равномерным движением называют движение тела, которое совершает равные перемещения в течение любых равных промежутков времени.

Скорость при равномерном движении определяется как отношение перемещения ко времени, в течение которого данное перемещение было совершено. Уравнение имеет следующий вид:

(vec{v}=frac{vec{s}}{t})

(vec{v}=const)

Проекция вектора скорости на ось ОХ выглядит таким образом:

(v_{x}=frac{s_{x}}{t})

(v_{x}=const)

Если вектор скорости спроецировать на ось координат, то она будет равна быстроте изменения данной координаты:

(v_{x}=frac{x-x_{0}}{t})

Прямолинейное равноускоренное движение

Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.

Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:

(vec{a}=const)

При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, необходимо выполнить следующий расчет:

(vec{v}=vec{v}_{0}+vec{a}t)

Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:

(v_{x}=v_{0x}+a_{x}t)

a>0, движение является равноускоренным.

Во время торможения в проекции на ось ОХ скорость рассчитывают следующим образом:

(v_{x}=v_{0x}-a_{x}t)

а<0, движение является равнозамедленным.

Графически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:

График ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, которая параллельна оси времени:

• график 1 находится над осью t, тело совершает разгон, ах>0;
• график 2 размещен под осью t, тело тормозит, ах<0.

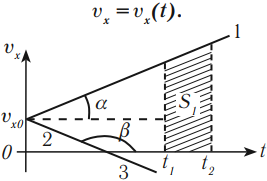
Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:

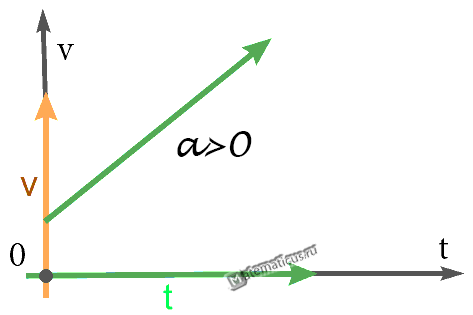
Графически скорость, характерная для равноускоренного движения тела, имеет вид прямой. График 1 направлен вверх, тело будет совершать равноускоренное движение в положительном направлении оси ОХ:

(v_{0x}>0)

(a_x>0)

(a_{1x} = tg α )

График 2 направлен вниз, тело будет двигаться равнозамедленно в положительном направлении оси ОХ:

(v_{0x}>0)

(a_x<0)

(a_{2x} = tg α )

График 3 направлен вниз, тело свершает равноускоренное движение против оси ОХ:

(v_{0x}<0)

(a_x<0)

Исходя из графика зависимости скорости от времени, определяют перемещение, которое тело преодолело в течение определенного промежутка времени (t_2-t_1). В этом случае целесообразно рассчитать площадь фигуры, расположенной под графиком. Формула для определения перемещения при равноускоренном движении имеет вид:

(S_{x}=v_{0x}t+frac{a_{x}t^{2}}{2})

(S_{x}=frac{v^{2}-v_{0}^{2}}{2a})

Перемещение в n-ую секунду во время равноускоренного движения можно определить по формуле:

(S_{n}=frac{a}{2}left(2n-1 right))

Определить координату тела, которое совершает равноускоренное движение, можно с помощью справедливого уравнения:

(x=x_{0}+v_{0x}t+frac{a_{x}t^{2}}{2})

Движение тела, брошенного вертикально вверх (вниз)

Во время падения тела вниз вектор его скорости направлен в ту же сторону, что и вектор ускорения свободного падения.

Формулы, описывающее это движения, имеют следующий вид:

(vec{v} ↑↑vec{g})

(h=v_{0}t+frac{gt^{2}}{2})

(v=v_{0}+gt)

(h=frac{v^{2}-v_{0}^{2}}{2g})

В случае, когда тело падает вниз и его начальная скорость равна нулю, (v_0=0). Время падения при этом можно рассчитать по формуле:

(t=sqrt{frac{2h_{0}}{g}})

(h) является начальной высотой.

Для брошенного вверх тела будут справедливы следующие равенства:

(h=v_{0}t-frac{gt^{2}}{2})

(v=v_{0}-gt)

(h=frac{v^{2}-v_{0}^{2}}{-2g})

В максимальной верхней точке тело, брошенное вверх, будет обладать нулевой скоростью, (v=0). Для расчета времени подъема можно воспользоваться формулой:

(t=frac{v_{0}}{g})

Свободно падающее тело

Свободным падением называют движение тела в условиях безвоздушного пространства под действием силы тяжести.

В условиях свободного падения ускорения тел с разной массой будут равны. Данный параметр называют ускорением свободного падения. Оно всегда направлено к центру нашей планеты, то есть вертикально вниз. Величина обозначается латинской буквой g, а единицами измерения являются м/с².

Ускорение свободного падения равно 9,8 м/с². В задачах по физике допускается использовать значение g=10 м/с².

Движение по окружности с постоянной по модулю скоростью

Движением по окружности при постоянной по модулю скоростью называют простейшим видом криволинейного движения.

Траектория такого движения будет представлена в виде окружности. Вектор скорости тела приобретает направление по касательной к окружности. Модуль скорости тела при изменении времени остается постоянным, а направление движения в каждой точке изменяется. Из этого можно сделать вывод, что движение по окружности представляет собой движение с ускорением. В свою очередь ускорение, изменяющее направление скорости, носит название центростремительного.

Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение является характеристикой быстроты изменения направления вектора линейной скорости. Параметр обозначается, как ацс. Единицами измерения центростремительного ускорения служат м/с². Формула для расчета следующая:

(а_{цс} = frac{v^{2}}{R})

Движение тела по окружности при постоянной по модулю скорости называют периодическим движением. Таким образом, его координата будет повторяться через одинаковые периоды времени. Периодом называют время, в течение которого тело совершает один полный оборот. Обозначается величина как Т. Единицами измерения периода являются секунды, с. Для расчета справедливо равенство:

(T=frac{t}{N})

(N) является количеством оборотов, (t) — временем, за которое тело совершает обороты.

Частота вращения представляет собой количество оборотов за единицу времени. Обозначается параметр в виде латинской буквы (ν). Единицами измерения являются (с^{-1}) (Гц).

(nu=frac{N}{t})

Период и частота являются взаимно обратными величинами:

(T=frac{1}{nu})

(nu =frac{1}{T})

Линейная скорость представляет собой скорость движения тела по окружности. Параметр обозначают латинской буквой v, единицами измерения являются м/с. Линейная скорость направлена по касательной к окружности и рассчитывается по формуле:

(v=frac{2pi times R}{T})

(R) является радиусом окружности.

Угловой скоростью называют физическую величину, которая определяется как отношение угла поворота и времени, за которое тело совершает этот поворот. Обозначают параметр как ω. Единицами измерения угловой скорости являются рад/с. Угловая скорость определяется по формуле:

(omega =frac{varphi }{t})

(varphi) представляет собой угол поворота.

Направление угловой скорости определяют с помощью правила правого винта или буравчика. В случае, когда вращательное движение винта соотносится с направлением движения тела по окружности, то поступательное движение винта и направление угловой скорости совпадают. Связь параметров движения тела по окружности представлена следующими формулами:

(v=omega R)

(omega =frac{v}{R})

(a_{сц} = omega ^{2}R)

(omega = frac{2pi }{T})

(omega = 2pi v)

Во время равномерного движения тела по окружности точки, расположенные на радиусе, перемещаются с равной угловой скоростью, так как радиус за одно и то же время поворачивается на одинаковый угол. В это время линейная скорость разных точек радиуса отличается в зависимости от того, насколько близко или далеко от центра они размещены:

(v_{1}=omega r)

(v_{2}=omega R)

(frac{v_{1}}{v_{2}}=frac{r}{R})

При рассмотрении равномерного движения двух соединенных тел можно наблюдать отсутствие отличий в линейных скоростях, но при этом угловые скорости тел будут различны в зависимости от радиуса тела:

(omega _{1}=frac{v}{R_{1}})

(omega _{2}=frac{v}{R_{2}})

(frac{omega _{1}}{omega _{2}}=frac{R_{1}}{R_{2}})

Движение тела, брошенного под углом к горизонту

Движение тела, которое бросили под углом к горизонту, можно представить в виде суперпозиции двух движений:

1. Равномерного горизонтального перемещения.
2. Равноускоренного движения вертикально при ускорении свободного падения.

Формула скорости будет иметь следующий вид:

(v_{0x}=v_{x}=v_{0} cos alpha =const)

(v_{0y}=v_{0}sin alpha)

(v_{y}=v_{0}sin alpha-gt)

Уравнение координаты обладает следующим видом:

(x=v_{0}cos alpha times t)

(y=v_{0}sin alpha times t-frac{gt^{2}}{2})

Скорость тела в любое время будет равна:

(v=sqrt{v_{x}^{2}+v_{y}^{2}})

Найти угол между вектором скорости и осью ОХ можно по формуле:

(tan beta =frac{v_{y}}{v_{x}}=frac{v_{0}sin alpha -gt}{v_{0}cos alpha })

Время подъема на максимальную высоту равно:

(t=frac{v_{0}sin alpha }{g})

Максимальную высоту подъема можно рассчитать с помощью формулы:

(h_{max}=frac{v_{0}^{2}sin ^{2}alpha}{2g})

Время полета соответствует уравнению:

(t=frac{2v_{0}sin alpha }{g})

Максимальную дальность полета можно рассчитать по формуле:

(L_{max}=frac{v_{0}^{2}sin 2alpha }{g})

Движение тела, брошенного горизонтально

Движение тела, которое бросили горизонтально, представлено в виде суперпозиции двух движений:

1. Равномерное горизонтальное движение со скоростью v0=v0x.
2. Равноускоренное вертикальное движение при ускорении свободного падения g с нулевой начальной скоростью.

Уравнение скорости:

(v_{x}=v_{0x}=const)

(v_{y}=g_{y}t=-gt)

Уравнение координаты:

(x=v_{0x}t=v_{x}t)

(y=frac{g_{y}t^{2}}{2}=h_{0}-frac{gt^{2}}{2})

Скорость тела в любое время будет определяться по формуле:

(v=sqrt{v_{x}^{2}+v_{y}^{2}})

Дальность полета тела соответствует уравнению:

(l=v_{0x}t=v_{0x}sqrt{frac{2h_{0}}{g}})

Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:

(tan beta =frac{v_{y}}{v_{x}}=frac{-gt}{v_{0x}})

Задачи по кинематике, их решение

Задача 1

Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч ((v_1)). Далее половину оставшегося времени он ехал со скоростью 6 км/ч ((v_2)). Остаток расстояния путник преодолел пешком со скоростью 4км/ч ((v_3)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.

Решение

Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:

(S = S_1 + S_2 + S_3)

(t = t_1 + t_2 + t_3)

На каждый отрезок пути необходимо составить уравнение движения:

(S_1 = v_1t_1)

(S_2 = v_2t_2)

(S_3 = v_3t_3)

Далее можно представить дополнительные условия задачи:

(S_1 = S_2 + S_3)

(t_2 = t_3)

(v_{sr}=frac{S}{t}=frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}})

Следует преобразить формулу и подставить числовые значения:

(v_{sr}=frac{2S_{1}}{frac{S_{1}}{v_{1}}+frac{2S_{1}}{v_{2}+v_{3}}}=frac{2v_{1}left(v_{2}+v_{3} right)}{2v_{1}+v_{2}+v_{3}})

(v_{sr}=frac{2times 12left(6+4 right)}{2times 12+6+4}=7)

Ответ: средняя скорость составляет (7) км/ч.

Задача 2

Тело подбросили вертикально вверх. Начальная скорость при этом составила 3,13 м/с ((v_0)). В момент, когда данное тело достигло максимальную высоту полета, из начального пункта подбросили второе тело с такой же начальной скоростью, как у первого. Необходимо определить на каком расстоянии от точки бросания встретятся тела. Сопротивлением воздуха при решении можно не учитывать.

Решение

Схематично перемещение тел можно представить следующим образом:

Формула, описывающая движение тела, которое подбросили вверх, необходима для вычисления координаты движущегося тела в любое время. Для первого тела справедливо уравнение:

(h=v_{0}t_{1}-frac{gt_{1}^{2}}{2})

Для второго тела можно представить следующую формулу:

(h=v_{0}t_{2}-frac{gt_{2}^{2}}{2})

Следующую формулу можно составить на основании условия задачи, в котором указано, что  второе тело бросили позднее первого на время максимального подъема:

(t_{1}-t_{2}=frac{v_{0}}{g})

Объединяя уравнения в систему из трех формул относительно величины (h) получим:

(h=frac{3}{4}frac{v_{0}^{2}}{2g})

(h=frac{3}{4}frac{3.13^{2}}{2*9.8}=0.37)

Ответ: тела встретятся на высоте (0,37) м.

Задача 3

Камень, находясь в свободном падении, вторую часть пути преодолел за 1 секунду. Необходимо вычислить высоту (h), с которой упал камень.

Решение

Ось Y системы координат, в которых падает камень, направлена вертикально вниз. В качестве начала координат можно принять точку, из которой камень упал. Закон перемещения данного тела в проекции на ось будет обладать следующим видом:

(h=v_{0}t+frac{gt^{2}}{2})

(h=frac{gt^{2}}{2})

(v=v_{0}t+gt)

(v=gt)

Время падения камня рассчитывается по формуле:

(t=sqrt{frac{2h}{g}})

Для середины пути, который преодолел камень, справедливы уравнения:

(frac{h}{2}=frac{gt_{1}^{2}}{2})

(t_{1}=sqrt{frac{h}{g}})

Время (t_2), которое потребовалось телу на преодоление второй половины пути, указанное в условии задачи, рассчитывается по формуле:

(t_{2}=t-t_{1}=sqrt{frac{2h}{g}}-sqrt{frac{h}{g}})

(t_{2}^{2}=frac{h}{g}left(sqrt{2} -1right)^{2})

Исходя из данного уравнения, можно вычислить высоту:

(t_{2}^{2}=frac{h}{g}left(sqrt{2} -1right)^{2})

(h=frac{t_{2}^{2}g}{left(sqrt{2}-1 right)^{2}}=frac{9,81}{0,17}=57,7)

Ответ: камень упал с высоты (57,7) м.

Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно применять справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.

Skip to content

Равномерное движение (движение тела с постоянной скоростью)

Формула скорости движения при равномерном движении:

v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении:

Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по  формуле:

График — Равномерного прямолинейного движения

Равноускоренное движение

Формула скорости при равноускоренном движении:

a=const
v₀ — начальная скорость, м/с
a — ускорение, м/с²
Формула для нахождения перемещения при равноускоренном движении:

или

Уравнение равноускоренного движения в проекции на оси координат:

Формула для определения ускорения при равноускоренном прямолинейном движении:

v₀ — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения:

График — Равноускоренное движение при a>0

Равнозамедленное движение

Равнозамедленное движение — это движение тела, при котором модуль скорости равномерно уменьшается с течением времени, а вектор ускорения остается постоянным как по модулю, так и по направлению.

Формула скорости при равнозамедленном движении:

Формула перемещения при равнозамедленном движении:

График — Равнозамедленное движение при a<0

Свободное падение

Постоянная величина скорости свободного падения тела равна g=9,8 м/с²
Формула для вычисления скорости при свободном падении тела:

Формула для вычисления перемещения при свободном падении тела:


Формула координаты при свободном падении тела:

Формула высоты с которой тело свободно падает:

Формула для определения скорости тела в конце свободного падения:

Время свободного падения тела равно:

61842

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»