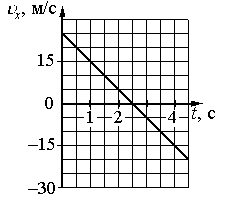Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Равноускоренное движение: формулы
Формула для скорости при равноускоренном движении:
Vк=Vн+at
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для ускорения при равноускоренном движении:
a=(Vк-Vн)/t
Во время движения тела ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула расстояния при равноускоренном движении
- Если известны время, скорость начальная и скорость конечная
S = t*(Vн+ Vк)/2
- Если известны время, скорость начальная и ускорение
S = Vнt + at2/2 = t*(Vн + at/2)
где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
2аS = Vк2−Vн2
где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.
Задача 2
Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графически
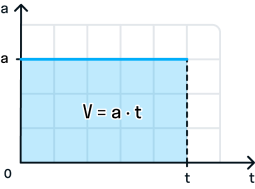
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
Взаимосвязь скорости, времени и расстояния:
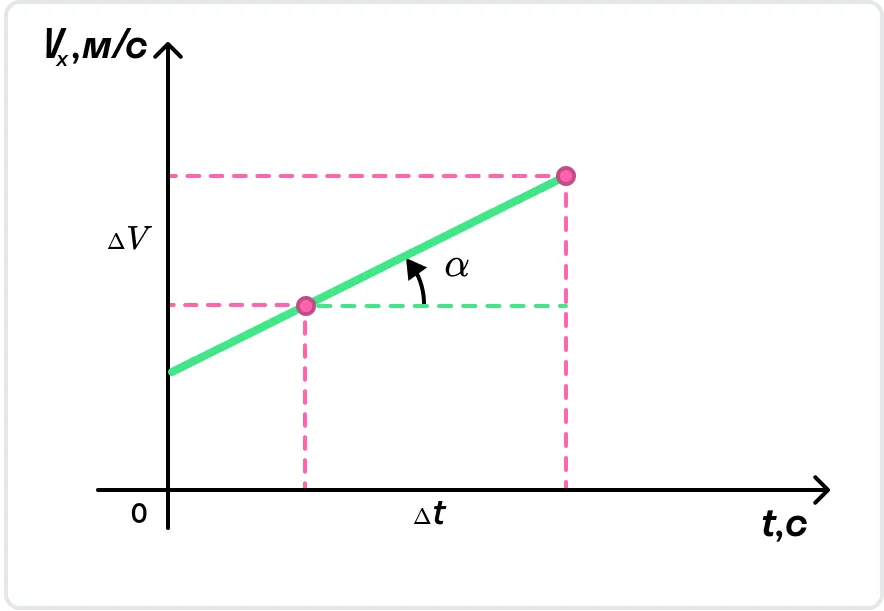
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
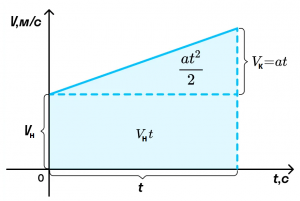
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.
Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*22 =6+6=12 м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
Проекция ускорения на ось ОХ
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
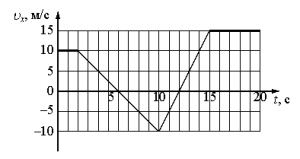
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.8k
Равноускоренное движение

4.7
Средняя оценка: 4.7
Всего получено оценок: 68.
Обновлено 28 Июля, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 68.
Обновлено 28 Июля, 2021
Одним из видов движения, изучаемых кинематикой, является равноускоренное движение. Равноускоренное движение — это достаточно распространённый вид движения, даже большинство равномерных движений начинались с разгона и были некоторое время равноускоренными. Рассмотрим эту тему подробнее, получим формулу равноускоренного движения, приведём примеры такого движения.
Ускорение
Если некоторое тело начинает движение из состояния покоя, то его скорость изменяется от нуля до некоторого максимального значения. Следовательно, при таком движении можно указать быстроту изменения скорости.
Например, в рекламе автомобилей указывается время разгона до 100 км/ч. Ясно, что модель, достигающая такой скорости за 5 секунд, значительно резвее, чем модель со временем разгона 15 секунд, хотя конечная скорость в обоих случаях одинакова. В чем же здесь разница, с точки зрения кинематики?
Разница в быстроте набора скорости.
Быстрота набора скорости называется ускорением. Ускорение (обозначается латинской буквой $a$) равно отношению величины набранной скорости ко времени этого увеличения:
$$overrightarrow a={overrightarrow {Δv}over t}={overrightarrow v- overrightarrow {v_0} over t}$$
где:
- $overrightarrow a$ — ускорение тела;
- $overrightarrow v$ — скорость тела в момент $t$;
- $overrightarrow {v_0}$ — начальная скорость тела (при $t=0$).
Из данной формулы можно получить размерность ускорения. Скорость измеряется в метрах в секунду, а время — в секундах, значит, ускорение измеряется в метрах в секунду за секунду (или метров в секунду в квадрате).
В приведённом примере первый автомобиль разгоняется с ускорением 5,56 метров в секунду за секунду, а второй — с ускорением 1,85 метров в секунду за секунду.
Равноускоренное движение
Движение, при котором ускорение тела постоянно, называется равноускоренным. При этом знак ускорения не играет роли. Движение с постоянным отрицательным ускорением также является равноускоренным, несмотря на то, что скорость уменьшается.
Наиболее частым примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха ещё не играет большой роли. Другим примером может служить разгон автомобиля при постоянном нажатии на педаль «газа», пока не будет набрана необходимая скорость.
Формулы равноускоренного движения
Найдём формулы скорости и координаты при равноускоренном движении. Из приведённого выше определения ускорения следует, что скорость при постоянном ускорении равна:
$$overrightarrow v= overrightarrow {v_0} + overrightarrow a t$$
Это — линейная зависимость. Её график представляет собой прямую, наклон которой зависит от значения $a$. Чем оно больше, тем круче поднимается график.
Из курса физики 9 класса известно, что перемещение тела равно площади под графиком скорости. А площадь под данной прямой представляет собой трапецию с высотой $t$ и основаниями $v$ и $v_0$. Как известно из геометрии, площадь трапеции равна произведению полусуммы оснований на высоту. То есть:
$$overrightarrow x= {(overrightarrow {v_0} + overrightarrow v)over 2} t$$
Подставив значение $v$ из предыдущей формулы и учтя, что в начальный момент времени координата была равна $x_0$, мы получим:
$$overrightarrow x= overrightarrow {x_0}+overrightarrow {v_0}t + {overrightarrow at^2 over 2}$$
Это основная формула равноускоренного движения, позволяющая найти координату $overrightarrow x$ материальной точки в момент времени $t$ при условии, что начальная координата была равна $overrightarrow x_0$, начальная скорость — $overrightarrow {v_0}$, а ускорение — $overrightarrow a$. В задачах она используется, как правило, совместно с предыдущей.
Что мы узнали?
Ускорение — это физическая величина, характеризующая быстроту набора скорости материальной точкой. Движение с постоянным ускорением называется равноускоренным. Хорошим примером равноускоренного движения является свободное падение тел.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 68.
А какая ваша оценка?
Равноускоренное движение.
-
Зависимость скорости от времени.
-
Закон движения.
-
Прямолинейное равноускоренное движение.
-
Свободное падение.
-
Горизонтальный бросок.
-
Бросок под углом к горизонту.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.
Равноускоренное движение — это движение с постоянным вектором ускорения . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.
к оглавлению ▴
Зависимость скорости от времени.
При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.
Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:
. (1)
В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор
? Разумеется, функцию
. Но не только: к ней можно добавить ещё произвольный постоянный вектор
(ведь производная постоянного вектора равна нулю). Таким образом,
. (2)
Каков смысл константы ? В начальный момент времени
скорость равна своему начальному значению:
. Поэтому, полагая
в формуле (2), получим:
.
Итак, константа — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:
. (3)
В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и
прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
, (4)
. (5)
Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)
к оглавлению ▴
Закон движения.
Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:
Подставляем сюда выражение для скорости, даваемое формулой (3):
(6)
Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить , надо продифференцировать функцию
. Чтобы получить
, нужно продифференцировать
. Не забудем добавить и произвольную константу
:
.
Ясно, что — это начальное значение
радиус-вектора
в момент времени
. В результате получаем искомый закон равноускоренного движения:
. (7)
Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:
. (8)
. (9)
. (10)
Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.
Снова вернёмся к закону движения (7). Заметим, что — перемещение тела. Тогда
получаем зависимость перемещения от времени:
.
к оглавлению ▴
Прямолинейное равноускоренное движение.
Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:
,
,
,
где — проекция перемещения на ось
.
Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:
и подставим в формулу для перемещения:
.
После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:
.
Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.
к оглавлению ▴
Свободное падение.
Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.
Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения , направленным вертикально вниз. Почти во всех задачах при расчётах полагают
м/с
.
Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.
Задача. Найти скорость приземления дождевой капли, если высота тучи км.
Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой
.
Имеем: — искомая скорость приземления,
. Получаем:
, откуда
. Вычисляем:
м/с. Это 720 км/ч, порядка скорости пули.
На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!
Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через
c.
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
.
Здесь , так что
. Вычисляем:
м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.
Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью
м/с. Через какое время камень упадёт на землю?
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
.
Имеем: так что
, или
. Решая квадратное уравнение, получим
c.
к оглавлению ▴
Горизонтальный бросок.
Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.
Предположим, что тело брошено горизонтально со скоростью с высоты
. Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.
Выберем систему координат так, как показано на рис. 1.
 |
| Рис. 1. Горизонтальный бросок |
Используем формулы:
В нашем случае . Получаем:
. (11)
Время полёта найдём из условия, что в момент падения координата тела
обращается в нуль:
.
Дальность полёта — это значение координаты
в момент времени
:
.
Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:
.
Получили зависимость от
, которая является уравнением параболы. Следовательно, тело летит по параболе.
к оглавлению ▴
Бросок под углом к горизонту.
Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.
Предположим, что тело брошено с поверхности Земли со скоростью , направленной под углом
к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.
Выберем систему координат так, как показано на рис. 2.
 |
| Рис. 2. Бросок под углом к горизонту |
Начинаем с уравнений:
,
.
В нашем случае . Получаем:
.
Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:
,
,
.
(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от
снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:
.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Равноускоренное движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023
Содержание:
- Определение и формула равноускоренного движения
- Основные кинематические величины при равноускоренном движении
- Примеры решения задач
Определение и формула равноускоренного движения
Определение
Движение, при котором за любые равные промежутки времени скорость меняется на одну величину, называют равнопеременным.
Если скорость при этом увеличивается, то такое движение носит название равноускоренного движения.
Равноускоренное движение можно определить еще как движение, при котором модуль касательного ускорения
($a_{tau}=$ const $>0$).
Основные кинематические величины при равноускоренном движении
Ускорение $bar{a}$ при равноускоренном движении находят как:
$$bar{a}=frac{bar{v}_{2}-bar{v}_{1}}{t}(1)$$
где v2 – конечная скорость, v1— начальнаяскорость движения, t–время движения.
Скорость в любой момент равноускоренного прямолинейного движения можно найти как:
$$bar{v}=bar{v}_{0}+bar{a} t(2)$$
где $bar{v}_0$ – начальная скорость движения.
Уравнение для координаты материальной при равноускоренном движении записывают как:
$$x=x_{0}+v_{0 x} t+frac{a_{x} t^{2}}{2}(2)$$
где v0x – проекция начальной скорости на ось X, ax – проекция ускорения на ось X.
Перемещение при равноускоренном движении является функцией вида:
$$bar{s}=bar{s}_{0}+bar{v}_{0} t+frac{bar{a} t^{2}}{2}(3)$$
где $bar{s}_0$ – перемещение в начальный момент времени.
Или $bar{s}$ еще можно представить как:
$$bar{s}=frac{bar{v}^{2}-bar{v}_{0}^{2}}{2 bar{a}}(4)$$
Примеры решения задач
Пример
Задание. Тело было брошено вертикально вверх. Оно возвратилось на землю через промежуток времени, равный t.
Какой была начальная скорость тела, и на какую высоту оно поднялось?
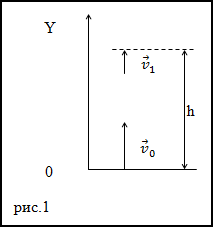
Решение. Тело в поле тяжести Земли движется с постоянным ускорением равным ускорению свободного
падения, на рис.1 оно направлено вниз.
В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:
$$bar{s}=bar{s}_{0}+bar{v}_{0} t+frac{bar{a} t^{2}}{2}$$
Все движение происходит только по оси Y, поэтому проекция выражения (1.1) примет вид:
$$y(t)=v_{0} t-frac{g t^{2}}{2}(1.2)$$
Формула для скорости при равноускоренном движении записывается как:
$$bar{v}=bar{v}_{0}+bar{a} t(1.3)$$
В проекции на ось она преобразуется к виду:
$$v(t)=v_{0}-g t(1.4)$$
Точке максимального подъема мы имеем y(t1)=h и v(t1)=0 (t1 — время поъема), тогда выражения (1.2)
и (1.4) перепишем как:
$$h=v_{0} t_{1}-frac{gleft(t_{1}right)^{2}}{2}, 0=v_{0}-g t_{1}(1.5)$$
где $t_{1}=frac{t}{2}$ . Следовательно,
$$v_{0}=frac{g t}{2}(1.6)$$
Подставляя выражение (1.6) вместо начальной скорости в формулу h, имеем:
$$h=frac{g t}{2} cdot frac{t}{2}-frac{gleft(frac{t}{2}right)^{2}}{2}=frac{g t^{2}}{8}$$
Ответ. $v_{0}=frac{g t}{2} ; h=frac{g t^{2}}{8}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Расстояние между двумя точками равно l. Первую половину пути тело проходит равноускорено,
вторую равнозамедленно. Максимальная скорость тела равна v. Каков модуль ускорения тела и время его перемещения, если
ускорения на обоих участках пути равны по модулю.
Решение. Данную задачу можно решить двумя способами.
1 способ аналитический.
В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:
$$bar{s}=bar{s}_{0}+bar{v}_{0} t+frac{bar{a} t^{2}}{2}(2.1)$$
Для первой половины пути, учитывая, что мы рассматриваем прямолинейное движение, запишем:
$$s=frac{a t_{1}^{2}}{2}(2.2)$$
где учтено, что $bar{s}_{0}=0, bar{v}_{0}=0, s=frac{l}{2}$ .
Для второй половины пути получаем:
$$s^{prime}=v t_{2}-frac{a t_{2}^{2}}{2}(2.3)$$
где $s^{prime}=frac{l}{2}$ .
Суммарное время, которое провело тело в пути равно:
$$t=t_{1}+t_{2}(2.4)$$
Наибольшая скорость движения равна:
$$v=a t_{1}=a t_{2} rightarrow t_{1}=t_{2}(2.5)$$
Суммарный путь равен:
$$l=frac{a t_{1}^{2}}{2}+v t_{2}-frac{a t_{2}^{2}}{2} rightarrow t_{2}=frac{l}{v}$$
Ускорение выразим из (2.2), имеем:
$$a=frac{l}{t_{1}^{2}}=frac{v^{2}}{l}$$
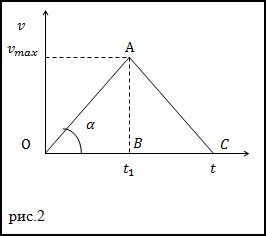
2.графический способ решения задачи.
Для этого построим график зависимости v(t).
Путь равен площади под кривой или в нашем случае сумме площадей треугольниковOABи ABC. Значит можно записать:
$$
begin{array}{c}
l=frac{v_{max } t_{1}}{2}+frac{v_{max } t_{2}}{2} rightarrow t=frac{2 l}{v_{max }}=frac{2 l}{v} \
a=operatorname{tg} alpha=frac{v_{max }}{t / 2}=frac{v^{2}}{l}
end{array}
$$
Ответ. $t=frac{2 l}{v}, a=frac{v^{2}}{l}$
Читать дальше: Формула силы Лоренца.