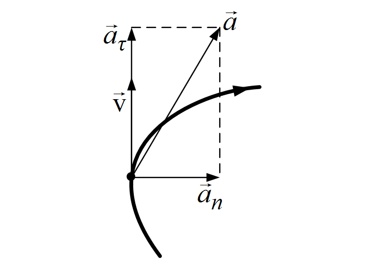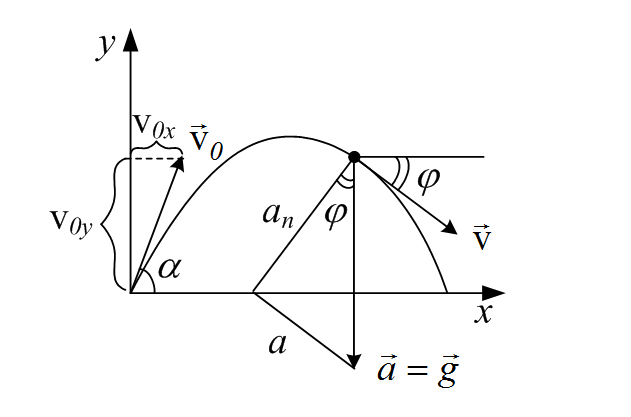Как найти ускорение примеры - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Ускорение характеризует быстроту изменения скорости движущегося тела.^[1] Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. ^[2] Ускорение измеряется в метрах в секунду за секунду (м/с²) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.

1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.^[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с².
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.^[4] Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = v_к — v_н и Δt = t_к — t_н, где v_к – конечная скорость, v_н – начальная скорость, t_к – конечное время, t_н – начальное время.^[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что t_н = 0.
3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (v_к — v_н)/(t_к — t_н). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v_к — v_н)/(t_к — t_н)
  - Напишите переменные: v_к = 46,1 м/с, v_н = 18,5 м/с, t_к = 2,47 с, t_н = 0 с.
  - Вычисление: a = (46,1 — 18,5)/2,47 = 11,17 м/с².
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
  - Напишите формулу: a = Δv / Δt = (v_к — v_н)/(t_к — t_н)
  - Напишите переменные: v_к = 0 м/с, v_н = 22,4 м/с, t_к = 2,55 с, t_н = 0 с.
  - Вычисление: а = (0 — 22,4)/2,55 = -8,78 м/с².
Реклама

1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.^[6] Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.
- Второй закон Ньютона описывается формулой: F_рез = m x a, где F_рез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с²).
2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.^[7] Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.
- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с².^[8]
4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с²
Реклама

Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:

Движение автомобиля	Изменение скорости	Значение и направление ускорения
Движется вправо (+) и ускоряется	+ → ++ (более положительное)	Положительное
Движется вправо (+) и замедляется	++ → + (менее положительное)	Отрицательное
Движется влево (-) и ускоряется	— → — (более отрицательное)	Отрицательное
Движется влево (-) и замедляется	— → — (менее отрицательное)	Положительное
Движется с постоянной скоростью	Не меняется	Равно 0

2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с². Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с².
3

Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):

Реклама

Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 — 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с².

Об этой статье

Эту страницу просматривали 190 509 раз.

Была ли эта статья полезной?

Источник

Как найти ускорение — определение и формулы расчета в физике

Содержание:

Что такое ускорение
- Единица измерения
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
Мгновенное ускорение
Максимальное ускорение
Среднее ускорение
Проекция ускорения

Что такое ускорение

Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.

Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.

Единица измерения

В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как рассчитать ускорение: формулы

Для прямолинейного движения

Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.

В этом случае ускорение находится по следующим формулам:

(a;=;frac{mathrm V}t)

(a;=;frac{2S}{t^2})

(a;=;frac{V^2}{2S})

Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V₀ и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

(overrightarrow a=frac{overrightarrow F}m)

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.

Выражается по формуле:

( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})

Максимальное ускорение

(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.

Среднее ускорение

Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.

Проекция ускорения

Определение проекции ускорения на ось (х):

(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.

Насколько полезной была для вас статья?

Рейтинг: 1.92 (Голосов: 36)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Скорость тела может меняться двояко. Она может:

1. увеличиваться;

2. уменьшаться.

Пример:

предположим, что самолёт начинает движение из состояния покоя, поэтому его начальная скорость равна нулю. Самолёт разгоняется, и его скорость постепенно увеличивается. В это время движение самолёта ускоряется.

Приближаясь к цели, пилот самолёта снижает скорость, движение становится всё медленнее и медленнее до остановки самолёта. На этом этапе пути движение замедляется.

Ускорение Замедление

Неравномерное движение может ускоряться или замедляться.

(t) — время движения.

Источник

Виталий Викторович Карабут

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Ускорение: сущность и виды

Под действием различных физических сил тела ускоряют или замедляют свое движение.

Определение 1

Ускорением называют интенсивность изменения скорости движения. Оно характеризует изменение скорости за единицу времени.

В системе СИ ускорение измеряется в метрах в секунду за секунду, иными словами, в метрах в секунду в квадрате ($м/с^2$).

Движение с ускорением, вектор которого не меняется по модулю и направлению, называется равноускоренным.

Определить ускорение при равноускоренном прямолинейном движении можно по формуле:

$a = frac{v_1 — v_0}{t} = frac{Delta v}{t}$,

где $v_1, v_0$ — скорости в начале и в конце рассматриваемого периода времени длительностью $t$.

Отношение изменения скорости к промежутку времени, за который произошло это изменение, называют средним ускорением:

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

$vec{a} = frac{vec{v_1} — vec{v_0}}{t} = frac{Delta vec{v}}{t}$,

В отличие от равноускоренного, здесь имеют значение направления векторов.

Если начальная скорость больше конечной, происходит замедление, которое в физике также принято называть ускорением, но выраженным с отрицательным знаком.

Мгновенное ускорение — ускорение, развиваемое за очень малый промежуток времени (его длительность стремится к нулю):

$vec{a} = limlimits_{t to 0}frac{Delta vec{v}}{Delta t}$.

Ускорение при движении по окружности

Поскольку ускорение — векторная величина, при движении отличном от прямолинейного оно не остается неизменным даже если модуль скорости не изменяется. В связи с этим ускорение вычисляется из начальной и конечной скоростей по правилам векторной математики, т.е. с учетом изменения направления.

Тело, движущееся по окружности, удобно рассматривать как обладающее двумя ускорениями: тангенциальным ($a_{tau}$), направленным по касательной к траектории, и центростремительным, направленным к центру ($a_n$). При равномерном движении по окружности тангенциальное ускорение, отражающее мгновенную скорость тела, может быть равно нулю, но центростремительное имеет место даже в этом случае. Поэтому любое движение по криволинейной траектории является движением с ускорением.

«Формулы ускорения в физике» 👇

Замечание 1

Центростремительное ускорение называется также нормальным, тангенциальное — касательным.

Касательное ускорение определяется как мгновенное при движении на очень малое угловое расстояние, когда длина дуги и длина хорды между начальной и конечной точками малоразличимы (сравниваются мгновенные скорости в этих точках).

Формула для определения центростремительного ускорения:

$a_n = frac{v^2}{R}$,

где $v$ — мгновенная скорость, $R$ — радиус траектории.

При движении по искривленной траектории величину результирующего ускорения получают из тангенциального и нормального исходя из теоремы Пифагора:

$vec{a}^2 = vec{a_{tau}}^2 + vec{a_n}^2 implies vec{a} = sqrt{vec{a_{tau}}^2 + vec{a_n}^2}$

Такое ускорение называется полным.

Пример 1

Найти ускорение тела, разгоняющегося за 10 с от 5 до 100 км/ч.

В начальный момент времени тело двигалось со скоростью

$v_{0} = frac{5000}{3600} approx 1,39 м/с.$

Скорость в конце интервала:

$v_{1} = frac{100000}{3600} approx 27,8 м/с.$

Подставив числовые значения в формулу, получаем:

$a = frac{v_1 — v_0}{t}$

$a = frac{27,8 — 1,39}{10} approx 2,64 м/с^{2}$

Ответ: ускорение составило $ 2,64 м/с^{2}$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Скорость тела в инерциальной системе отсчета может изменяться под действием внешних воздействий на тело. Ускорение является характеристикой этого изменения.

Определение и физический смысл

Ускорение для скорости является тем же самым, что скорость для радиус-вектора: производной по времени.

Мгновенным ускорением называется первая производная по времени от мгновенной скорости:

a→=dv→dtoverrightarrow{a}=frac{doverrightarrow{v}}{dt}

Средним ускорением называется отношение вектора изменения скорости материальной точки, которая состоялась за время Δt,Δt, к величине времени ΔtΔt:

aср→=Δv→Δtoverrightarrow{{{a}_{ср}}}=frac{Delta overrightarrow{v}}{Delta t}

Единицей измерения ускорения в системе СИ является метр, разделенный на секунду в квадрате – м /с².

Физический смысл ускорения заключается в том, что ускорение — это физическая величина, которая показывает, как со временем меняется скорость тела.

Пример 1

Вычисление ускорения
Координаты материальной точки, движущейся в плоскости xy, определяются формулами:

x=At4+Bt2,x = At^4 + Bt^2, y=Ct3−t,y = Ct^3- t, где A=0,25м/с4A = 0,25 м/с^4; $B = 0,5 м / с²; C=1/3м/с3;C = 1/3 м / с^3; D=1м/с.D = 1 м / с.

Найти вектор ускорения и его модуль.

Решение

Продифференцируем выражения для проекций скорости по времени и получим проекции координаты вектора ускорения в нужный момент времени:

ax=ddt(t3+ t)=3⋅t2+1=3⋅12+1=4ax = frac{d}{dt}({{t}^{3}}+text{ }t)=3cdot {{t}^{2}}+1=3cdot {{1}^{2}}+1=4 м/с²;

ay=ddt(t2+1)=2⋅t=2⋅1=2ay = frac{d}{dt}({{t}^{2}}+1)=2cdot t=2cdot 1=2 м/с².

Вектор скорости:

a⃗=2⋅(2⋅i⃗+j⃗)vec{a}=2cdot (2cdot vec{i}+vec{j}) м/с².

Его модуль:

a=ax2+ay2=42+22=25≈4,5a=sqrt{a_{x}^{2}+a_{y}^{2}}=sqrt{4_{{}}^{2}+2_{{}}^{2}}=2sqrt{5}approx 4,5 м/с

Нормальное и тангенциальное ускорения

Рассматривая движение материальной точки по криволинейной траектории, удобно вектор полного ускорения разложить на две взаимно перпендикулярных компоненты: aτa_τ –тангенциальное и ana_n –нормальное ускорение:

Вектор тангенциального ускорения имеет направление вдоль касательной, а нормальное ускорение — вдоль нормали к траектории. Модуль тангенциального ускорения является первой производной по времени от модуля скорости:

Модуль нормального ускорения зависит от радиуса кривизны траектории в данной точке траектории и модуля скорости:

∣a⃗τ∣=aτ=v˙|{vec{a}}_{tau}|={a}_{tau}={dot{v}}

Вектор полного ускорения является векторной суммой тангенциального и нормального ускорений:

a⃗=a⃗τ+a⃗nvec{a}={{vec{a}}_{tau }}+{{vec{a}}_{n}}

Модуль полного ускорения находят по теореме Пифагора:

a=∣a⃗∣=aτ2+an2=v˙2+v4R2a=|{vec{a}}|=sqrt{a_{tau }^{2}+a_{n}^{2}}=sqrt{{{{dot{v}}}^{2}}+frac{{{v}}^{4}}{{{R}^{2}}}}

Движение точки называется ускоренным, если численное значение ее скорости увеличивается со временем, то есть а>0а > 0 движение точки называется замедленным, если численное значение ее скорости уменьшается со временем, то есть а<0а < 0. Если aτ=0a_τ = 0, то материальная точка совершает равномерное движение, а если an=0a_n = 0 – движение по прямой (прямолинейное движение). Величины aτa_τ и ana_n характиризуют скорость изменения в соответствии с численным значением и направлением скорости движущейся материальной точки.

Пример 2

Тело подбросили под углом α к горизонту. Для момента времени, когда вектор скорости будет составлять угол ϕ=30∘phi=30^{circ} с горизонтальной линией. Найти: 1) нормальное, 2) тангенциальное, 3) полное ускорение.

Решение

Полное ускорение– это ускорение свободного падения a=ga=g. Из рисунка получим^

an=gcos⁡ϕ=9,8cos⁡30∘≈8,49 /2{{a}_{n}}=gcos phi =9,8cos {{30}^{circ }}approx 8,49text{ }/{{}^{2}},

aτ=gsin⁡ϕ=9,8sin⁡30∘≈4,90 /2{{a}_{tau }}=gsin phi =9,8sin {{30}^{circ }}approx 4,90text{ }/{{}^{2}},

a=an2+aτ2=a=sqrt{a_{n}^{2}+a_{tau }^{2}}=

=8,492+4,902≈9,8 /2.=sqrt{{{8,49}^{2}}+{{4,90}^{2}}}approx 9,8text{ }/{{}^{2}}.

Ответ: an≈8,49 /2{{a}_{n}}approx 8,49text{ }/{{}^{2}}, aτ≈4,90 /2{{a}_{tau }}approx 4,90text{ }/{{}^{2}}, a≈9,8 /2.aapprox 9,8text{ }/{{}^{2}}.

Тест по теме «Ускорение тела»

Источник