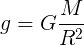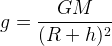Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
- Мой первый физический эксперимент.
- Определение ускорения свободного падения с помощью математического маятника.
- Надо делать все по-другому…
- Ускорение свободного падения и закон всемирного тяготения
- Ускорение свободного падения на различных широтах
- Как найти ускорение свободного падения на Марсе???
Мой первый физический эксперимент.
Свой самый первый физический эксперимент с гравитацией я поставил более 30 лет назад, когда мне было года 4 наверно.
Я скинул кота с балкона. К счастью, он остался жив, и даже позже сам повторил этот опыт, пытаясь поймать голубя. И опять же остался жив. Несмотря на то, что это был пятый этаж. Не даром говорят, что у кошек девять жизней.
Но так или иначе прошу вас не повторять мои ошибки, и не ставить опыты над животными. Или как Эрвин Шредингер делайте их мысленно.
Определение ускорения свободного падения с помощью математического маятника.
Здравствуйте дорогие друзья, меня зовут Валентин Анатольевич и сегодня я покажу вам как рассчитать ускорение свободного падения, не кидая котов с балкона.
Итак, нам понадобится яблоко и шнурок. Ну или толстая леска как в моем случае. Соединяем леску с яблоком. И получаем некое подобие математического маятника.
Я эту конструкцию называю яблотник. Моя последняя разработка.
Время, за которое маятник совершает полное колебание называется периодом. В нашем случае это время полета яблока туда и обратно. У меня оно составило 1,4 секунды.
Для математических маятников период определяется по следующему уравнению:
![[T=2pi sqrt{frac{l}{g}}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-29425af3eec4256686ccf44fde46b3ca_l3.png "Rendered by QuickLaTeX.com")
Где 
— это длинна маятника, а 
— ускорение свободного падения. Его нам и необходимо найти. Вспоминаем зачем нам нужна алгебра и выражаем .
![[g=frac{4pi^2 l}{T^2}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-e8bc79a4cb27f61bdf76660aa84a3c55_l3.png "Rendered by QuickLaTeX.com")
Осталось только с помощью линейки найти длину нашего яблотника и произвести расчеты.
Обратите внимание, так как в нашем случае яблоко не является материальной точкой и его размерами пренебречь не получится, за длину маятника мы будем брать длину лески плюс половинку высоты яблока. Я намерил 49 сантиметров.
Подставляем значения и считаем.
![[g=frac{43,14^2 cdot 0,49}{1,4^2}= 9,8596]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-d9ac9bff379d8962193472ccb4f7d7c7_l3.png "Rendered by QuickLaTeX.com")
Получается примерно 9.86 м/с 2
Надо делать все по-другому…
Да!!! По-хорошему стоило сделать по-другому. Позволить маятнику совершить несколько колебаний, потом общее время за которое эти колебания были совершены поделить на их количество, тем самым получить среднее значение периода колебаний, и только после этого производить расчеты.
Да и посчитать погрешность так же не помешало бы…
Ну, зато теперь вы знаете, как увлекательно провести выходные.
Ускорение свободного падения и закон всемирного тяготения
При желании ускорение свободного падения можно вычислить из закона всемирного тяготения. Сила, с которой тела притягиваются к Земле вычисляется по следующему уравнению:
![[vec F= Gfrac {M m}{R^2}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-a6f611b8b574fce8e4ae44c091f6c8e9_l3.png "Rendered by QuickLaTeX.com")
Где F- сила тяжести, G — гравитационная постоянная, М — масса Земли, m — масса тела, а R — расстояние между их центрами масс. Если тело находится непосредственно на поверхности Земли, то за R можно принять её радиус.
Согласно второму закону Ньютона, сила тяжести, действующая на тело равна произведению массы тела на ускорение свободного падения.
![[vec F= m vec g]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-2022ccb6ee33f752946935fe60def1cf_l3.png "Rendered by QuickLaTeX.com")
Приравниваем правые части наших уравнений и сокращаем массу.
![[vec g= Gfrac {M}{R^2}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-04437c091816b4e0cc36bb3613fda492_l3.png "Rendered by QuickLaTeX.com")
Осталось только подставить все необходимые значения переменных и произвести расчеты.
![[vec g= 6,672 cdot 10^{-11}frac {5,976 cdot 10^{24}}{(6,371 cdot 10^6)^2} approx 9,82]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-06121b4359f69d0da05ab3797f93f3c9_l3.png "Rendered by QuickLaTeX.com")
Получается 9.82 м/с 2. Все как в учебнике по Физике. И самое главное ни один котик не пострадал.
Ускорение свободного падения на различных широтах
Стоит отметить, что для расчетов я брал усреднённое значение радиуса Земли. В реальности ускорение свободного будет изменяться в зависимости от широты.
Так экваториальный радиус больше, чем полярный, соответственно на полюсах ускорение свободного падения будет чуть выше, чем на экваторе.
| Широта | g, м/с2 |
| 0° | 9.78030 |
| 10° | 9.78186 |
| 20° | 9.78634 |
| 30° | 9.79321 |
| 40° | 9.80166 |
| 50° | 9.81066 |
| 60° | 9.81914 |
| 70° | 9.82606 |
| 80° | 9.83058 |
| 90° | 9.83216 |
А если учесть еще и неровности рельефа, горы холмы…. В общем выходит довольно переменчивая константа.
Как найти ускорение свободного падения на Марсе???
А какое ускорение свободного падения на Марсе? И какой период колебаний будет там у нашего маятника? Пишите в комментариях. Ну а я с вами прощаюсь. Желаю счастья и до скорых встреч.
Как найти ускорение свободного падения
Для того чтобы найти ускорение свободного падения, сбросьте достаточно тяжелое тело, желательно металлическое, с некоторой высоты и засеките время падения, затем по формуле рассчитайте ускорение свободного падения. Или измерьте силу тяжести, которая действует на тело известной массы и поделите значение силы на эту массу. Можно использовать математический маятник.
Вам понадобится
- электронный и обычный секундомер, металлическое тело, весы, динамометр и математический маятник.
Инструкция
Нахождение ускорения свободного падения свободно падающего телаВозьмите металлическое тело, и прикрепите его к кронштейну на некоторой высоте, которую сразу измерьте в метрах. Внизу остановите специальную платформу. Кронштейн и платформу присоедините к электронному секундомеру. Высота должна быть подобрана таким образом, чтобы сопротивлением воздуха можно было пренебречь. Рекомендуется выбирать высоты от 2 до 4 м. После этого отсоедините тело от кронштейна, в результате оно начнет свободно падать. После удара о платформу секундомер зафиксирует время падения в секундах. После этого поделите значение высоты на значение времени, взятое во второй степени, а результат умножьте на 2. Получите значение ускорения свободного падения в м/с2.
Нахождение ускорения свободного падения через силу тяжести Измерьте на весах массу тела в килограммах с высокой точностью. Затем, возьмите динамометр и подвесьте на него это тело. Но покажет значение силы тяжести в ньютонах. После этого поделите значение силы тяжести на массу тела. В результате получите ускорение свободного падения.
Нахождение ускорения свободного падения с помощью математического маятника Возьмите математический маятник (тело, подвешенное на достаточно длинной нити) и заставьте его колебаться, предварительно измерив длину нити в метрах. Включите секундомер и отсчитайте некоторое количество колебаний и засеките время в секундах, за которое они были произведены. После этого поделите количество колебаний на время в секундах, а полученное число возведите во вторую степень. Затем умножьте его на длину маятника и число 39,48. В результате получим ускорение свободного падения.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В статье обсуждается несколько подходов к нахождению ускорения свободного падения.
Ускорение свободного падения — это ускорение свободного падения объекта в вакууме с равномерной скоростью, несмотря на его массу, из-за силы тяжести. С помощью законов Ньютона, которые описывают силу тяжести, мы можем обнаружить ускорение силы тяжести или ускорение силы тяжести.
Ускорение свободного падения зависит от гравитирующего тела большой массы M, но не зависит от тела m малой массы. Вот почему тела небольшой массы падают вниз к гравитирующему телу, несмотря на его массу. Поэтому ускорение свободного падения называют ускорение свободного падения or ускорение силы тяжести, обозначается как ‘g’.
Поскольку сила вызывает такое ускорение, мы можем определить значение g с помощью нескольких подходов, использующих Законы движения Ньютона.
Прочтите, как рассчитать массу по гравитационной силе.
Как найти ускорение свободного падения с помощью законов Ньютона
Давайте рассчитаем значение g, используя второй закон движения Ньютона и закон всемирного тяготения.
Второй закон движения Ньютона дает силу тяжести между объектом и землей, тогда как закон всемирного тяготения дает силу гравитации между двумя объектами. Когда мы сравниваем обе силы гравитации, мы получаем значение ускорения свободного падения g.
Сила тяжести Fg определяется Второй закон Ньютона является,
Fg = мг …………………… .. (1)
Сила тяжести Fg определяется закон всемирного тяготения является,
Fg=GMм/об2
Где M — масса гравитирующего объекта, т. Е. Земли.
r — расстояние между центром масс объекта и земли.
А G — постоянная гравитационной пропорциональности.
Сравнивая обе силы тяжести Fg в уравнениях (1) и (2),
мг=ГМм/р2
г=ГМм/мр2
г=Гм/р2
Вышеупомянутая формула является стандартной формулой для расчета ускорения свободного падения g.
Как вы заметили, масса падающего тела m аннулируется при определении g, так как гравитационное ускорение зависит только от гравитации земной массы M.
Узнайте больше о законах Ньютона.
Рассчитайте ускорение свободного падения шара, падающего на земная поверхность. Масса земли 6 х 1024 кг, а расстояние между объектом и землей составляет 6.38 X 106 м. (G = 6.67 x 10-11 Нм2/ кг2)
Данный:
М = 6 х 1024 kg
г = 6.38 Х 106 m
G = 6.67 х 10-11 Nm2/ кг2
Найти: g =?
Формула:
Fg = мг
Решения:
Сила тяжести из-за Второй закон Ньютона находится в движении,
Fg = мг
г=Фg/m
Подставляя закон гравитации формулу (2) в приведенное выше уравнение,
г=ГМм/мр2
г=Гм/р2
Подставляя все значения,
г = 9.86
Ускорение свободного падения падающего у земной поверхности шара составляет 9.86 м / с.2.
Сила тяжести — это сила тяжести, которая различна для разных масс M. Следовательно, значение g также немного отличается для других планет из-за разной массы..
Прочтите, как рассчитать массу по силе и расстоянию.
Луна имеет массу 7.35 X 10.22 кг, а расстояние между центром масс 1.74 X 106м. Вычислите ускорение свободного падения космонавта, идущего по Луне.
Данный:
М = 7.35 х 1022 kg
г = 1.74 Х 106m
G = 6.67 х 10-11 Nm2/ кг2
Найти: г =?
Формула:
г=ГМ/р2
Решения:
Ускорение свободного падения космонавта рассчитывается с использованием Законы Ньютона,
г=ГМ/р2
Подставляя все значения,
г = 1.619
Ускорение свободного падения космонавта на Луне составляет 1.619 м / с.2.
Если объект движется на определенной высоте h от гравитирующей поверхности; подобно тому, как спутник вращается на высоте h от земли, радиус между ними становится R (r + h). Следовательно, величина ускорения свободного падения g также изменяется из-за изменения радиуса r.
Узнать больше о наклонной плоскости.
Если спутник движется по орбите на высоте около 280 км над земной поверхностью, какое гравитационное ускорение он испытывает?
Данный:
М = 6 х 1024 kg
G = 6.67 х 10-11 Nm2/ кг2
г = 6.38 Х 106 m
h = 280 км = 0.28 X 106 m
R = (r + h) = (6.38 Х 106 + 0.28 Х 106) = 6.66 х 106 m
Найти: g =?
Формула:
г=ГМ/р2
Решения:
Ускорение свободного падения рассчитывается с использованием Законы Ньютона,
г=ГМ/р2
Подставляя все значения,
г = 9.02
Ускорение свободного падения на спутнике, вращающемся над землей, составляет 9.02 м / с.2.
Как найти ускорение свободного падения с помощью третьего закона Кеплера
Рассчитаем значение g, используя Третий закон Кеплера следующим образом:
Третий закон Кеплера касается орбитального движения планет, согласно которому период обращения по орбите пропорционален ее большой полуоси. Период времени планеты получается путем сравнения центростремительной силы и силы тяжести, обусловленной законом всемирного тяготения.
(Кредит: Shutterstock)
Компания центростремительная сила на орбитальной планете
Fc=мв2/r
Сравнение центростремительная сила уравнение (4) с закон всемирного тяготения (2)
mv2/ г = Гм/р2
v2=ГМ/р
Скорость = Расстояние / Время
Расстояние до планеты, когда она движется по орбите = 2πr
v=2πr/T
v2=4π2r2
Подставляя указанное выше уравнение в уравнение (5),
4p2r2/T2=ГМ/р
T2=4π2r3/ГМ
Выше уравнение период времени на орбите планеты.
Давайте выведем гравитационное ускорение формула по времени.
Используя уравнение (3), M=gr2/G
Подставляя значение M в уравнение (6),
T2=4π2r3/гр2
г=4π2р/т2
Вот как мы можем вычислить значение g, используя период обращения объекта T.
Спутнику, движущемуся по орбите около 500 км, требуется 90 минут, чтобы совершить один оборот вокруг Земли. Какое будет гравитационное ускорение, которое он испытывает?
Данный:
г = 6.38 Х 106 m
h = 500 км
R = (R + h) = 6.88 Х 106 m
T = 90 мин. = 90 X 60 = 5.4 X 103 сек
Найти: g =?
Формула:
г=4π2р/т2
Решения:
Ускорение свободного падения на орбитальном спутнике рассчитывается по формуле
г=4π2р/т2
Подставляя все значения,
г = 9.28
Ускорение свободного падения на орбитальном спутнике Земли составляет 9.28 м / с.2
Узнать больше об угловом движении.
Как найти ускорение свободного падения, используя сферически-симметричные тела
Рассчитаем значение g для сферически симметричных тел следующим образом:
Гравитационно притягивающие тела обладают сферически-симметричным распределением массы, поскольку вся их масса сосредоточена в его центре. Следовательно, мы можем достичь ускорения свободного падения для симметричных тел, используя закон всемирного тяготения Ньютона.
(Кредит: физика)
Поскольку, масса = плотность / объем
Когда тела, имеющие симметричное распределение массы,
Где ρ0 плотность объекта
Подставляя приведенное выше уравнение в Закон тяготения Ньютона уравнение (2)
Подставляя Уравнение второго закона Ньютона (1) в приведенное выше уравнение,
Вот как мы можем вычислить значение g, используя плотность объекта ρ0.
Рассчитайте ускорение свободного падения шара, падающего на землю, который имеет плотность около 17 кг / см.3.
Данный:
G = 6.67 х 10-11 Nm2/ кг2
г = 6.38 Х 106 m
ρ0 = 17 кг / см3 = 17 х 103 г / см3
Найти: g =?
Формула:
Решения:
Ускорение свободного падения шара рассчитывается по формуле
Подставляя все значения,
г=(2893.71*10-2) / 3
г = 9.64
Ускорение свободного падения при падении мяча на землю составляет 9.64 м / с.2
Свободное падение — это движение тела под действием силы тяжести. В упрощенном виде расчет производится без учета сопротивления воздуха.
На поверхности Земли ускорение свободного падения имеет величину от 9,78 м/с2 на экваторе до 9,82 м/с2 на полюсах.
Кроме того, на планете существуют места с экстремальными значениями, которые не вписываются в математическую модель. Минимум составляет
9,76 м/с2, максимум — 9,83 м/с2. Для расчетов в физике используется усредненная величина — 9,8 м/с2
Формула ускорения свободного падения:
Ускорение свободного падения вычисляется по следующей формуле:
где
G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10-11 м3/(кг*с2), или Н*м2/кг2
R — расстояние, на котором находится тело от центра планеты
M — масса планеты
Как видно из вышеприведенной формулы, значение ускорения свободного падения обратно пропорционально квадрату расстояния от центра планеты,
т.е. зависит не только от радиуса самой планеты, но от того, на какой высоте над ее поверхностью находится тело.
Поэтому для расчёта величины «g» на определенной высоте формулу можно скорректировать вот таким образом:
где
G — гравитационная постоянная
R — радиус планеты
h — высота над поверхностью планеты, на которой находится тело
M — масса планеты
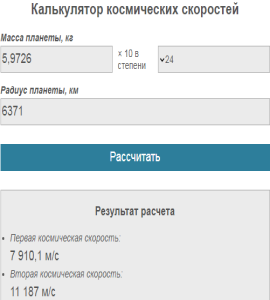
Для расчёта можно воспользоваться калькулятором, который приведен ниже.
Калькулятор ускорения свободного падения
Другие формулы
