Масса Солнца.
Масса Солнца составляет 1,9885 · 1030 кг или 333 082 масс Земли.
Масса и плотность Солнца
Сила тяжести и ускорение свободного падения на Солнце
Первая космическая скорость и вторая космическая скорость на Солнце
Изменение массы Солнца
Масса Солнца, Меркурия, Венеры, Земли, Луны, Марса, Юпитера, Сатурна, Урана, Нептуна
Масса и плотность Солнца:
Масса Солнца составляет 1,9885 · 1030 кг или 333 082 масс Земли. Масса Земли при этом составляет 5,97· 1024 кг.
Масса Солнца составляет 99,866 % от суммарной массы всей Солнечной системы.
Масса, как физическая величина, является мерой гравитационных свойств тела (гравитации, притяжения) и мерой его инертности. Соответственно различают гравитационную массу тела и инертную массу тела. В современной физике гравитационная масса и инертная масса считаются равными.
Как следствие проявления гравитационных свойств и действия закона всемирного тяготения два тела притягиваются друг к другу тем сильнее, чем больше их массы. Или чем больше масса тела, тем с большей силой она притягивает другие тела. Гравитационная масса определяет меру такого гравитационного притяжения (силы гравитационного притяжения).
Согласно закону всемирного тяготения сила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделёнными расстоянием r, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния:
F = G · m1 · m2 / r2 ,
где G – гравитационная постоянная, равная примерно 6,67⋅10−11 м³/(кг·с²).
При этом масса тела не зависит от скорости движения тела и остается неизменным при любых процессах.
Масса измеряется в килограммах и относится к одной из семи основных единиц Международной системы единиц (СИ).
Исходя из массы Солнца, как физической величины рассчитываются и другие параметры нашей звезды: плотность, ускорение свободного падения, сила тяжести, первая космическая скорость, вторая космическая скорость и пр.
Средняя плотность Солнца (ρ) – 1,408 г/см³ или 1408 кг/м³. Для сравнения: средняя плотность Земли (ρ) – 5,5153 г/см³.
Сила тяжести и ускорение свободного падения на Солнце:
Ускорение свободного падения на Солнце (g) составляет 274 м/с2 или 27,93 g Земли. Для сравнения: на Земле ускорение свободного падения составляет 9,81 м/с2 и меняется от 9,832 м/с² на полюсах до 9,78 м/с² на экваторе.
Ускорение свободного падения рассчитывается по формуле:
g = G⋅(M/r2) ,
где
М – масса планеты (звезды), кг,
r2 – квадрат радиуса планеты (звезды), м.
Сила тяжести на Солнце в 27,93 раз больше, чем на Земле. Это означает, что человек, весящий 72 кг, будет весить на Солнце всего 2 010,96 кг, т.е. около 2 тонн. Если быть точнее, то вес человека на Земле равен 72 кг · 9,81 м/с2 = 706,32 Н, а вес на Солнце равен 72 кг · 274 м/с2 = 19 728 Н. В то время масса человека на Солнце (72 кг) будет одинаковой, что и на Земле (72 кг).
Вес – это сила, с которой любое тело, находящееся в поле сил тяжести (как правило, создаваемое каким-либо небесным телом, например, Землёй, Солнцем и т. д.), действует на опору или подвес, препятствующие свободному падению тела. Вес тела, покоящегося в инерциальной системе отсчёта, равен силе тяжести, действующей на тело. Сила тяжести – это сила притяжения тела к небесному телу.
Вес (сила тяжести) рассчитывается по формуле F = m·g ,
где
F – сила тяжести, Н,
m – масса тела, кг,
g – ускорение свободного падения, м/с2.
На планетах Солнечной системы человек массой 72 кг будет весить:
– на Луне – 11,952 кг,
– на Меркурии – 27,159 кг,
– на Венере – 65,45 кг,
– на Земле – 72 кг,
– на Марсе – 27,241 кг,
– на Юпитере – 170,208 кг,
– на Сатурне – 76,6 кг,
– на Уране – 65,09 кг,
– на Нептуне – 82,08 кг,
– на Плутоне – 4,536 кг.
Первая космическая скорость и вторая космическая скорость на Солнце:
Первая космическая скорость (v1) на Солнце равна 437 км/с. Для сравнения: первая космическая скорость на Земле равна 7,91 км/с.
Первая космическая скорость (круговая скорость) – это минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Первая космическая скорость определяется массой и радиусом небесного тела, а также высотой над его поверхностью.
Первая космическая скорость вычисляется по формулам:
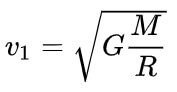
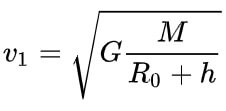
где
М – масса планеты, кг,
R – радиус орбиты, м,
R0 – радиус планеты, м,
h – высота над поверхностью планеты, м.
Вторая космическая скорость (v2) на Солнце равна 617,7 км/с. Она в 55,19 раза больше второй космической скорости на Земле. Для сравнения: вторая космическая скорость на Земле равна 11,19 км/с.
Вторая космическая скорость (параболическая скорость, скорость освобождения, скорость убегания) – это наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.
Вторая космическая скорость определяется радиусом и массой небесного тела.
Вторая космическая скорость вычисляется по формулам:
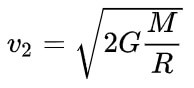
.
Изменение массы Солнца:
В ядре Солнца осуществляется протон-протонная термоядерная реакция с образованием гелия-4, потому каждую секунду в излучение превращаются 4,26 миллиона тонн вещества. В среднем Солнце излучает с ветром около 1,3⋅1036 частиц в секунду. Однако эта величина потерь ничтожна мала по сравнению с массой Солнца. Полная потеря массы Солнцем составляет за год 2 – 3⋅10−14 солнечных масс. Потеря за 150 миллионов лет эквивалентна земной массе.
Выброс вещества из солнечной короны Солнца называют корональным выбросом массы. Выброс включает в себя плазму, состоящую в основном из электронов и протонов наряду с небольшим количеством более тяжёлых ионизированных химических элементов – гелия, водорода, кислорода и других.
Поток ионизированных частиц (в основном гелиево-водородной плазмы), истекающий из солнечной короны со скоростью 300-1200 км/с, называемый солнечным ветром, уносится в окружающее космическое пространство.
Источник: https://ru.wikipedia.org/wiki/Солнце, https://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
3 069
Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Условие задачи:
Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца в 108 раз больше радиуса Земли, а плотность в 4 раза меньше плотности Земли? ((g=9,8) м/с2)
Задача №2.5.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(R_с=108R_з), (rho_с=0,25rho_з), (g_з=9,8) м/с2, (g_с-?)
Решение задачи:
[g = Gfrac{M}{{{R^2}}};;;;(1)]
Массу планеты можно найти из её средней плотности (rho) и объема (V):
[M = rho cdot V;;;;(2)]
Планеты обычно имеют форму, близкую к шарообразной, поэтому объем (V) можно посчитать по следующей формуле:
[V = frac{4}{3}pi {R^3};;;;(3)]
Подставим выражения (2) и (3) в формулу (1), тогда:
[g = Gfrac{{4rho cdot pi {R^3}}}{{3{R^2}}} = frac{4}{3}pi Grho R]
Видно, что ускорение свободного падения вблизи поверхности некоторой планеты зависит линейно от средней плотности и радиуса планеты. Учитывая это, ускорения свободного падения на Земли и на Солнце можно определить по следующим формулам:
[left{ begin{gathered}
g_c = frac{4}{3}Gpi rho_с R_с hfill \
g_з = frac{4}{3}Gpi rho_з R_з hfill \
end{gathered} right.]
Разделим верхнее равенство на нижнее:
[frac{{{g_с}}}{{{g_з}}} = frac{{{rho _с}{R_с}}}{{{rho _з}{R_з}}}]
Поэтому:
[g_с = g_зfrac{{{rho _с}{R_с}}}{{{rho _з}{R_з}}}]
Так как в условии сказано, что (R_с=108R_з) и (rho_с=0,25rho_з), то:
[g_с = g_зfrac{{0,25{rho _з} cdot 108{R_з}}}{{{rho _з}{R_з}}} = 27g_з]
Осталось посчитать численный ответ:
[g = 27 cdot 9,8 = 264,6; м/с^2]
Ответ: 264,6 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.5.4 Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения
2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.7 Определить первую космическую скорость для планеты, масса и радиус которой в два
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

